基于Vague集的目标优先级求解方法
刘欣怡,单甘霖,王一川
(军械工程学院,石家庄 050003)
基于Vague集的目标优先级求解方法
刘欣怡,单甘霖,王一川
(军械工程学院,石家庄 050003)
针对地面防空武器系统中目标优先级排序问题,建立了基于Vague集的目标优先级的模型。首先分析并量化了优先级影响因素中的定性指标和定量指标,建立了基于Vague集目标优先级决策矩阵;其次,针对传统基于Vague集目标优先级求解问题中影响因素权重难以确定问题,提出了基于Vague值距离测度最大化原理的权重确定方法,该方法有效地避免了权重选择的主观性;最后根据综合贴近度进行优先级的排序。算例仿真验证了该方法的可行性和有效性。
Vague集,目标优先级,权重,Vague值距离测度
0 引言
在地面防空武器系统中,目标优先级排序是实时科学作战决策的前提,对实现信息优势到决策优势进而到全维优势的转化具有极大影响。例如在目标检测、跟踪、识别阶段,当空域内要求同时处理的目标超出整个传感器网络的处理负荷时,应选择更需要关注的高优先级目标执行任务;在目标打击阶段,目标优先级评估是武器目标分配问题中关键技术之一。因此,研究适用于地面防空武器系统的目标优先级排序算法具有现实而又重要的意义。
目标优先级排序是涉及多领域、多层次的不确定性知识推理问题。目前主要有层次分析法[1][2]、多属性决策法[3]、神经网络法[4]等。文献[5]首次将Vague集用于多准则模糊决策问题。经过十多年的发展,Vague集已经广泛应用于各种不确定性多准则决策问题,见文献[6-10]。本文首先分析了目标优先级的主要影响因素并将其量化,建立了基于Vague集的多目标优先级求解模型;提出了基于Vague距离测度最大化原理的目标属性权重确定方法,最后通过计算相对贴近度得到目标优先级排序。
1 目标优先级影响因素及其量化
1.1 目标优先级影响因素
目标优先级评估必须建立在对目标信息科学的分析和综合之上。对地面防空武器系统而言,目标优先级主要根据上级是否指定、是否有攻击意图、攻击何种目标、目标机型等因素综合判断。本文主要考虑以下6个方面的因素:
(1)目标类型。目标类型反映了目标信号特征,将其按威胁度从大到小排列如下:第1类:战术弹道导弹;第2类:空地导弹、反辐射导弹;第3类:巡航导弹、大型轰炸机;第4类:指挥机;第5类:直升机;第6类:干扰机、侦察机。
(2)目标速度。同一目标飞行速度越大,威胁程度越大,目标优先级也就越高。
(3)飞临时间。飞临时间是指目标到达防空火力发射区近界的时间。其值越小,武器系统和战术决策的准备时间越短,威胁度越高。
(4)目标飞行距离。目标飞行距离是指目标与我方防区的距离,其值越小,目标优先级越高。
(5)目标航向角。航向角越小,目标的攻击意图越明显,目标的威胁度越大。
(6)目标干扰能力。目标的电子干扰将会影响我方的雷达指示和导弹制导的精度,其电子干扰能力越强,目标优先级越高,反之则越小。
1.2 目标优先级的量化
1.2.1 Vague集基本理论
定义1:令U是一个点(对象)的空间,其中任意一个元素用x表示,U中的一个Vague集V用一个真隶属度函数tV(x)和一个假隶属函数fV(x)表示,tV(x)是从支持的证据所到处的隶属度下界,fV(x)是从反对的证据所到处的否定隶属度下界,tV(x)和fV(x)将区间[0,1]中的一个实数与U中的每一个点联系起来,即:

其中0≤tV(x)+fV(x)≤1。
元素x在Vague集V的隶属度被区间[0,1]的一个子区间所界定,称之为Vague值。称为x相对于集V的Vague度,表示元素x相对于集V的不确定程度。
1.2.2 定量指标的Vague值
对于定量指标,比如目标速度,飞临时间等,通常由传感器测量并得到具体的实值,而并不是以Vague集的形式给出的。由于不同指标往往具有不同的量纲和量纲单位,为了消除他们带来的不可公度性,采用极变差法对定量指标作无量纲化处理。
对于效益型(越大越好)指标,如飞临时间,飞行距离等,其规范化Vague值度量方法如下:
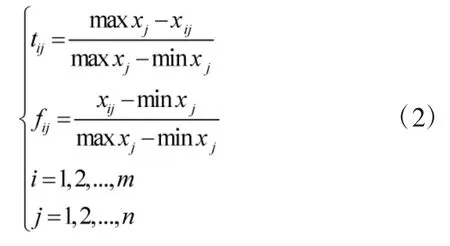
对于成本型(越小越好)指标,如飞行速度,其规范化Vague值度量方法如下:

1.2.3 定性指标的Vague值
定性指标对于“优先级高”这一概念的隶属度和非隶属度难以用具体的公式进行处理,可以通过语言术语集[11]来表示,本文根据相关人员作战经验给出参考,见表1所示。

表1 Vague值表示的语言变量(11级)
2 基于Vague距离测度最大化原理目标属性权重求解
基于Vague集的多属性决策问题中目标属性权值的确定问题并没有得到很好的解决。多数文献采用的主观赋权法虽然在一定程度上有效地结合了专家经验,但不同专家对目标属性有不同的偏好造成结果不一致。鉴于此,本文将目标优先级排序问题看作目标属性权重完全未知的不确定多属性决策问题,基于离差最大化思想上,提出基于Vague距离测度最大化原理的目标属性权重确定方法。
2.1 基于Vague集的多目标决策问题描述
假设A是决策目标集,A={A1,A2,…,Am},C是目标属性集,C={C1,C2,…,Cn},决策目标Ai在目标属性Cj下的特征由Vague集表示如下:

其中tij表示决策目标Ai关于目标属性Cj的满足程度,πij(x)=1-tij(x)-fij(x)表示决策目标Ai关于目标属性Cj的不确定程度。0≤tV(x)+fV(x)≤1,i=1,2,…,m,j=1,2,…,n。决策矩阵M有如下形式:

在目标优先级排序问题中,决策目标集A即为多个或批次目标组成的多目标集合,目标属性集C即为目标优先级的影响因素。
2.2 目标属性权重求解
对于空中目标优先级排序问题,假设已知决策矩阵M的情况下,影响因素的权重信息完全未知,假设各目标属性权重向量为ω=(ω1,ω2,…,ωn),ωj≥0,j=1,2,…,n,并满足单位化约束条件:

对目标优先级排序问题,若所有目标在目标属性Cj下的属性值差异越小,则说明该因素对目标优先级的排序所起的作用越小;反之如果目标属性Cj使所有目标的属性值有较大差异,则说明其对目标优先级的排序将起重要的作用。因此,从对目标优先级排序的角度考虑,目标属性值偏差越大的影响因素应该赋予越大的权重。如果所有目标在目标属性Cj下的Vague值没有差异,则目标属性对目标优先级排序不起作用,可令权值为0。
本文定义Hamming距离[12]为Vague值距离测度:设x,y是U中的两个Vague值,x=[tx,1-fx],y=[ty,1-fy]。则x和y之间的距离测度dw为:

对于目标优先级影响因素Cj,定义Vij(ω)表示目标xi与其他所有目标之间的Vague值距离:
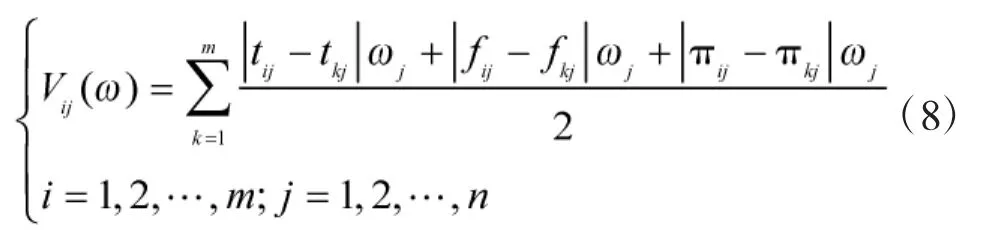
定义Vj(ω)表示对目标优先级影响因素Cj而言,所有目标与其他目标的总Vague值距离:

根据上述目标属性权重求解问题分析,权向量ω的选取应该使得所有目标属性对所有目标的总Vague值距离最大,为此构造目标函数V(ω):

于是,目标属性权重ω的求解等价于求解如下最优化模型:

对V(ω)做拉格朗日(Lagrange)函数:

对其求偏导数,有:

则可求得最优解:

进行归一化处理,得到目标属性权重:

得到目标属性权重以后,修正矩阵M得到决策矩阵S:

由式(15)求得目标属性权重,即得到了基于Vague值距离测度最大化原理求解到的目标优先级各影响因素的权重,该方法在假设目标属性权重完全未知的情况下客观的确定了目标属性的权重,避免了主观赋值法因为专家偏好不同而结果不同的问题,为后续优先级排序提供了可靠的决策矩阵。
3 优先级排序
决策矩阵S中每个元素包含了肯定、否定以及弃权的三维信息,这样的处理方法能更加精确化处理战场信息。但从决策矩阵S中并不能直观地看出目标优先级的大小,需要一种算法对评价值的隶属度信息进行比较和排序。本文借鉴多属性决策理论中逼近理想解的排序(TOPSIS)思想,基于Vague值距离测度进行比较和排序,具体方法如下:
(1)对目标优先级影响因素Cj,不同目标的评价值构成一组Vague值,可以确定正理想值和负理想值:

可以证明v+与v-也是Vague值,详见参考文献[7]。


(3)计算目标xi到理想解的相对贴近度ui:

相对贴近度ui越大,则目标xi优先级越高。按照ui的大小对m个目标进行优先级排序。
4 算法仿真
假设我方为一地面防空武器系统,在某一时刻,警戒雷达探测到空中有7批目标与我方阵地防御任务相关,并且没有接到上级指定的目标优先级。通过地面防空武器系统传感器获取目标信息,得到7批目标的属性参数如表2所示。
Step1:利用式(2)、式(3)和表1,实现对目标属性的量化,得到未经修正的决策矩阵M,见式(20)。

表2 目标属性参数
Step2:根据式(15)求解基于Vague值距离测度最大化原理的目标属性权重ω:

并由式(16)得到修正后的决策矩阵S。
Step3:根据式(17),确定正理想方案v+和负理想方案v-:



表3 各目标贴近度

Step5:由每个目标贴近度ui确定目标优先级排序(从高到低):x5>x4>x2>x1>x6>x7>x3。
关联仿真结果,目标5的优先级最高,目标4次之,结合仿真场景可以看出,该方法是可行并且有效的。
5 结束语
目标优先级评估是地面防空武器系统中的一个重要步骤,应用于多个方面,其结果直接影响战术决策,是提高系统效能的前提,也是实时科学作战决策的前提。本文结合Vague集理论与TOPSIS思想求解目标优先级,同文献[8-10]相比,利用Vague值距离测度客观的获得了目标优先级影响因素的权值,避免了权重选择的主观性。算例表明本文方法在目标优先级排序问题中是可行和有效的。
本文提出的基于Vague值距离测度最大化原理求解目标属性权重方法也可应用于其他属性变量为Vague值的多属性决策问题中。但该方法所确定的属性权重仍为实数型权重,如何进一步扩展为Vague型是下一步有待研究的问题。
[1]李家宽,杨惠珍,谢会桄.基于群体AHP的仿真可信度评估方法研究[J].系统仿真学报,2010,22(9):2065-2067.
[2]张堃,周德云.熵权与群组AHP相结合的TOPSIS法多目标威胁评估[J].系统仿真学报,2008,20(7):1661-1664.
[3]周林,娄寿春,赵杰.基于MADM的威胁评估排序模型[J].系统工程与电子技术,2001,23(1):18-19.
[4]王改革,郭立红.基于Elman-AdaBoost强预测器的目标威胁评估模型及算法[J].电子学报,2012,40(5): 907-906.
[5] Chen S M,Tan J M. Handling Multi-criteria Fuzzy Decision-making Problems Based on Vague Set Theory[J]. Fuzzy Sets and Systems,2000,114:103-113.
[6]万树平.基于Vague集的多传感器目标识别方法[J].控制与决策,2009,24(7):1097-1099,1103.
[7]耿涛,卢广山,张安.基于Vague集的空中目标威胁评估群决策方法[J].系统工程与电子技术,2011,33(12): 2686-2690.
[8]彭方明,邢清华.基于Vague集TOPSIS法的空中目标威胁评估[J].电光与控制,2010,17(10):23-26.
[9]童俊,单甘霖.基于Vague集的TOPSIS法求解目标优先级[J].火力与指挥控制,2012,37(5):140-143,147.
[10]夏璐,邢清华,范海雄.Vague物元及熵权的空袭目标威胁评估[J].火力与指挥控制,2012,37(2):84-88.
[11]周晓光,高学东,武森.基于理想解的Vague物元决策方法及其应用[J].北京科技大学学报,2009,31(1): 123-127.
[12]权双燕.模糊集之间的距离测度[J].计算机工程与应用,2008,44(26):65-67,70.
Method Based on Vague Set for Target Priority
LIU Xin-yi,SHAN Gan-lin,WANG Yi-chuan
(Ordnance Engineering College Shijiazhuang 050003,China)
A method based on Vague set for the problem of target priority of Land-Based Air Defence Weapon Systems is proposed.Firstly,the qualitative and quantitative indexes that affect target priority are analyzed and confirmed,and a decision-making matrix is established based on Vague set.Then,this paper principally studies the way to calculate the weights of the indexes by making the Vague distance maximum. Finally,the target priority algorithm is given according to the overall similarity degree.The application example is given and the results validated the applicability an effectiveness of this method.
Vague set,target priority,weight,Vague distance
TP391
A
1002-0640(2015)03-0087-05
2014-02-15
2014-03-29
刘欣怡(1990- ),女,重庆人,硕士研究生。研究方向:火控、指控及制导系统理论与应用。

