锚泊船舶纵向安全领域特性研究

艾万政

（浙江海洋学院海运与港航建筑工程学院，浙江舟山 316022）

船舶锚泊是船舶的经常性行为，锚泊安全研究是船舶航行安全研究的重要课题之一[1]。锚泊船舶的安全领域，是锚地规划及驾驶人员采取正确抛锚方法的重要依据。最早提出船舶领域概念的是20世纪60年代日本学者藤井弥平[2-3]。直到现在，该理论普遍应用于分析船舶避碰原理及航行水域的船舶交通流量状况。藤井弥平指出，船舶领域是一船驾驶员将其他船舶和固定物体保持在外的围绕该中心船的有效水域范围（船舶领域模型如图1）。该领域一般可认为是一个椭圆形，领域的大小与船舶尺度、航速以及环境状况有关，对于限制水域，当船舶以正常速度航行时，其满域尺寸的平均值在船首尾线方向上一般取6倍船长，横向上一般取1.6倍船长，为了保证船舶航行安全，领域和领域之间还应间隔一定的距离。

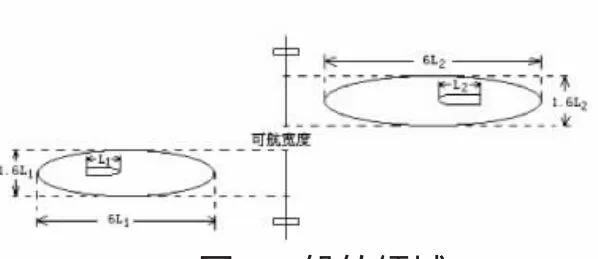
图1 船舶领域Fig.1 Ship's domain

船舶领域概念的提出，虽然对船舶的安全航行具有重要指导意义，但是该理论是在统计大量观测数据的基础上提出的，较少从水流角度来考虑问题[4-5]。事实上，船舶领域并不是一个静态的概念，船舶领域的大小并不是在任何时候横向上是6倍的船长，垂向上是1.6倍船长，船舶领域的大小势必会受到水流条件和气象条件的约束。因此，有必要从动态的眼光去讨论船舶领域。本文的目的，就是要针对锚泊船舶行为特性，运用数值模拟的方法，从水力学角度去研究其纵向领域范围，为锚地规划和锚泊船舶操纵提供参考。

1 数值计算模型

本文拟采用RNG k-ε模型来研究锚泊船舶领域。RNG k-ε模型的控制方程包括质量守恒方程、动量守恒方程、紊动能方程（k方程）和紊动能耗散率方程（ε方程），这四个方程共同构成一封闭的方程组。对于恒定且不可压缩的二维流动情况，它们的具体表达形式如下[6]：

连续性方程（质量守恒方程）：

式中：μi为速度分量；xi为坐标分量；ρ为水的密度；p为压强，k为湍动能，ε为湍动耗散率，Sij为应变率张量，Gk为由平均速度梯度引起的湍动能k的产生项，μ为动力粘度，μt为湍动粘度系数。边界处理如下：入流边界：给定入流的时均速度分布，湍动能分布和湍动能耗散率分布。其相应的表达式为：km=0.0144U2inε=k1.5in/（0.25D）。公式中：Uin为入口处的时均速度，kin为紊动能系数；ε为紊动能耗散率系数；D为河道半径。出流边界：出流被认为是充分发展的紊流，在该断面上各变量的法向梯度均为零。

2 计算方法分析

锚泊船舶附近的流速可以分解成两部分：一部分是沿锚泊船舶方向的分流速（用Ux表示），另一部分是与垂直船舶的分流速（用Uy表示）。由于船长方向分流速Ux对船舶运动的影响较小，而分流速Uy的方向可以是流向锚泊船，也可以是从锚泊船流去，Uy对船舶运动产生的作用可能是“船吸”，也可能是“船推”，这部分水流对船舶运动最不利，因此本文将Uy消失点（Uy=0）到锚泊船的最大距离定义为锚泊船舶纵向领域，用L表示（如图2所示）。

相关研究表明，固定物体的领域范围是附近水流的雷诺数及弗劳德数的函数，即：

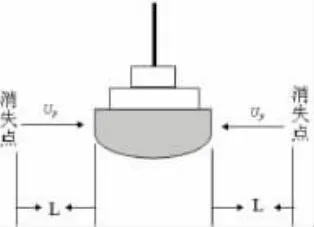
图2 船舶纵向领域范围Fig.2 The scope of ship's longitudinal domain

上式中：B是船舶宽度，ρ是水流密度，μ是水流的动力粘度，g是重力加速度，h是水深，u是流速。由于在常温下，水流密度、动力粘度、重力加速度均变化不大，同时，对于一般河道来说，船舶的领域范围随水深的增加而增大，而最大水深是水流表面的深度，因此水流表面处船舶的领域范围最大。从通航安全的角度考虑，考虑船舶最大领域范围对船舶安全有利。通过以上分析，可以认为，锚泊船舶最大纵向领域可近似表达为：

公式（6）中：U为航道表面流速。数值计算的工况设置就是按照公式（6）进行。

3 计算结果讨论

计算结果如表1所示。根据表1中的数据，将U=18 cm/s时的L随B的变化关系绘制成图3。由图3可以看出，当流速不变时，锚泊船舶的纵向安全领域与船宽成线性关系。图4是当B不变（B=25 m）时，L随流速U的变化关系。从图4可以看出，当锚泊船宽度不变时，锚泊船舶的纵向安全领域与流速几乎成二次曲线关系。对表1中的数据进行回归分析，可以得出锚泊船舶纵向安全领域的经验表达式如下：

公式（7）的实用条件为：U=18(cm/s)～50(cm/s)，U 的单位是 cm/s；B=25(m)～150(m)，B 的单位是 m。从公式（7）可以看出，锚泊船舶的纵向安全领域是随着表面流速的变化而变化，因此，船舶领域的概念应该是一个动态的概念，并不完全是静态的。

表1 计算结果数据Tab.1 The results data of calculation

图3 船舶纵向领域与船宽的关系Fig.3 The relationship between ship longitudinal domain and ship width

图3 船舶纵向领域与流速之间的关系Fig.4 The relationship between ship longitudinal domain and flow velocity

4 结论

数值模拟的结果表明，锚泊船舶的纵向领域与船舶宽度成线性关系，与航道表面的流速成二次曲线关系。通过回归分析得到了锚泊船舶纵向领域的经验表达式。研究结果还表明，船舶领域应该是一个动态的概念，而并非是一个完全静态的概念。

[1]谭 箭.弯窄航道通航单船最大平面尺度的确定方法初探[J].水运科技信息,1998(6):9-10.

[2]杨志军,艾万政.具有弯曲特性河道上桥梁通航宽度的探讨[J].水运工程,2007(3):65-70.

[3]FUJII Y.Some factors Affecting the Frequency of Accidents in Marine Traffic[J].Journal of Navigation,1974,27(2):235-252.

[4]PEDERSEN P T,ZHANG S.The Mechanics of Ship Impacts against Bridge[C]//Proceedings of Int.symposium advances on ship collision analysis.Copenhagen,1998:41-52.

[5]刘明俊.船舶过弯道所需航宽建模[J].武汉理工大学学报:交通科学与工程版,2006(1):15-23.

[6]张建明,等.突缩突扩式内消能工的数值模拟研究[J].水利学报,2004(12):29-33.