灰色GRM（1，1）模型的改进

何 俊， 刘银萍

（郑州升达经贸管理学院 共科部，河南 郑州 451191）

0 引 言

从传统的GM（1，1）模型的建模机理来看，当原始序列为单调递减时，由于其一次累加生成序列是单调递增的，其模拟值是递增的，对模拟值进行累减还原成原始序列的预测值时，就会产生不合理的计算误差。很多学者通过各种变换，如反向累加生成、倒数变换、线性变换，把递减序列变换成递增序列，再建立GM（1，1）模型［1－3］。文献［3］针对原始序列为单调递减的情况，提出了倒数累加生成及灰色GRM（1，1）模型，增强了灰色模型的适应性。但是，背景值z（1）（k）＝λx（1）（k－1）＋（1－λ）x（1）（k）中的参数λ的估计繁琐，导致背景值的计算复杂。结合文献［3－5］将灰色GRM（1，1）模型的背景值改进为

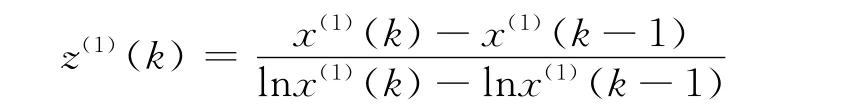
虽然简化了相关参数的计算，但是在发展系数的绝对值较大时，模型的预测精度不高。究其原因，是由于认为x（1）（k）服从齐次指数增长规律。而事实上当原始序列x（0）（k）服从齐次指数增长规律时，其一次累加生成序列x（1）（k）服从非齐次指数增长规律［6］。在此理论基础上，文献［6］将背景值优化为：

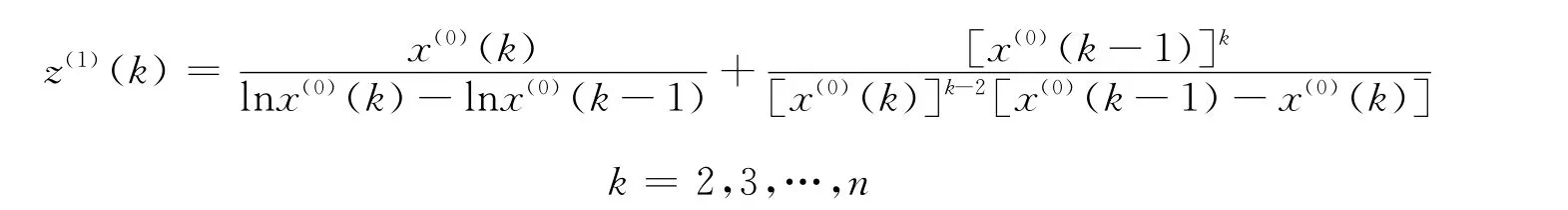
使得灰色模型的拟合和预测精度大大提高。此外，传统的GM（1，1）模型，将X（1）的第1个分量x（1）（1）作为初始条件，这是不合理的。文献［7］根据新信息优先原理，将X（1）的第n个分量x（1）（n）作为初始条件。通过以上分析，文中考虑将文献［6］和［7］两种优化方法结合起来，对GRM（1，1）模型进行优化，从而提高了模型的模拟与预测精度。

1 GRM（1，1）模型建模机理

定理1［5］设原始序列X（0）的倒数序列为

其中

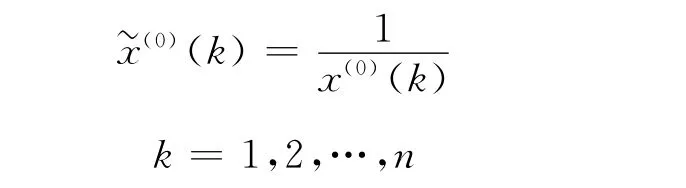
对X（0）作一次倒数累加生成序列

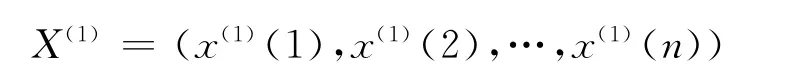
其中

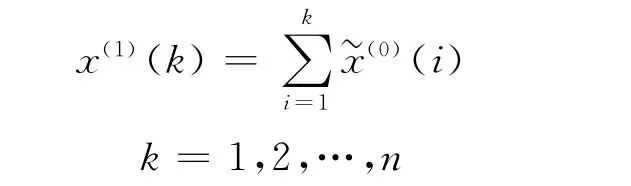
对X（1）建立GM（1，1）模型：

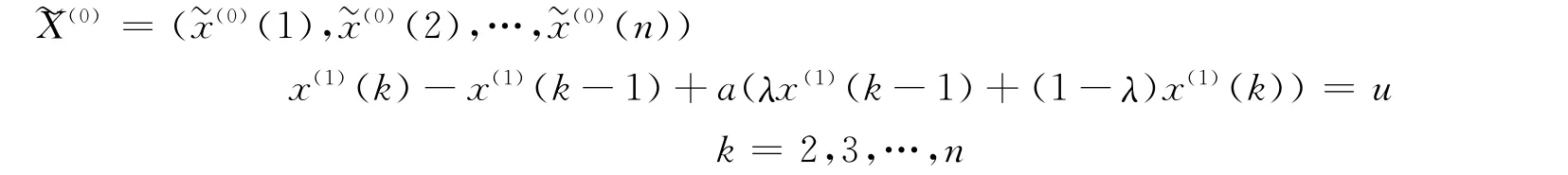
式中：λ——已知常数；

a——发展灰数；

u——内性控制灰数。

白化形式的微分方程为：

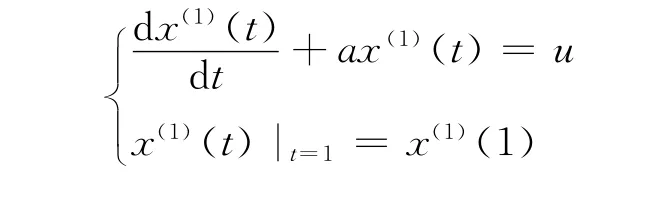
则

1）参数α＝（a，u）T可由最小二乘法求出

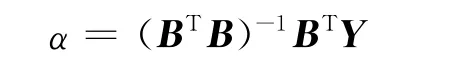
其中

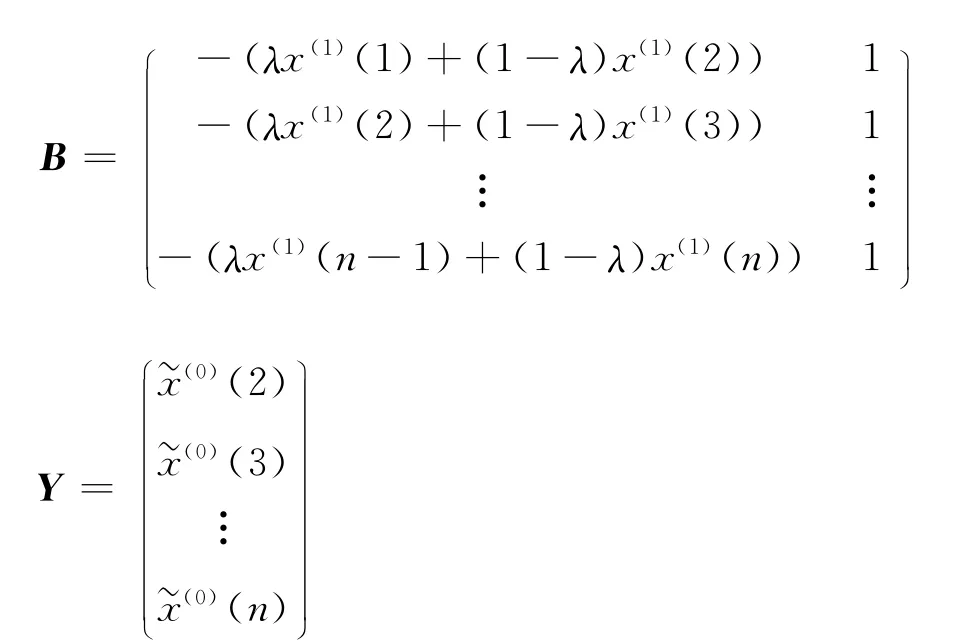
2）连续型响应函数为

3）离散型响应函数为

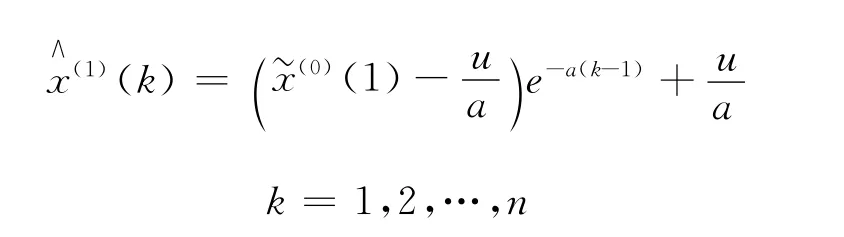
4）原始序列的模拟值为

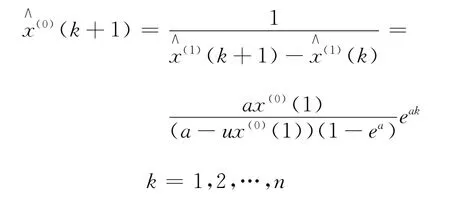
2 GRM（1，1）模型的改进

定理2 设X（0）为原始序列

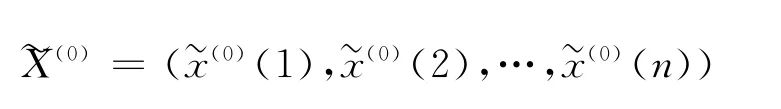
为X（0）的倒数序列，X（1）是X（0）的一次倒数累加生成序列，对X（1）建立GM（1，1）模型：

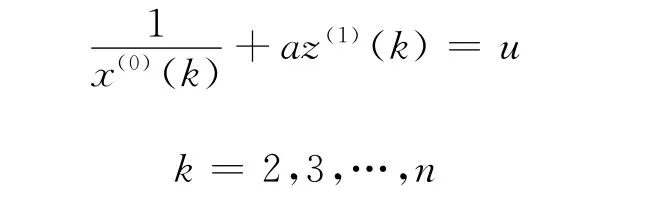
其中

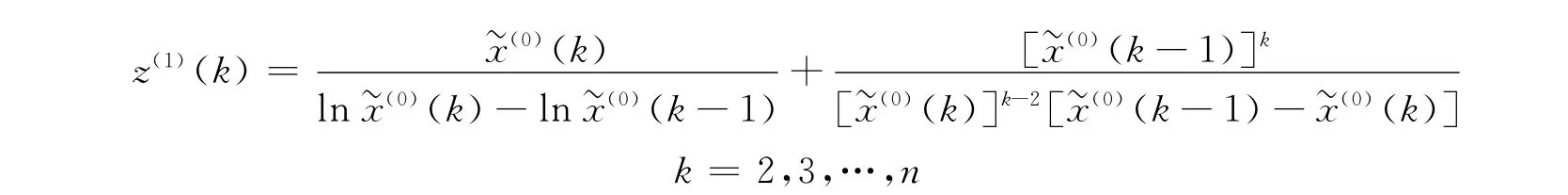
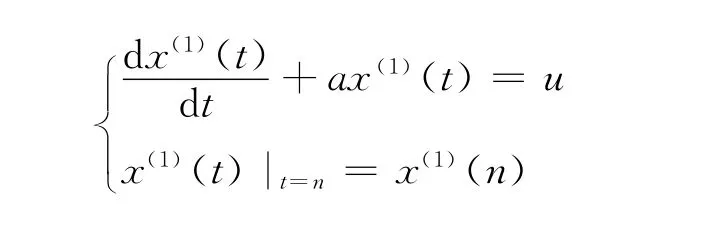
1）参数α＝（a，u）T可由最小二乘法求出：

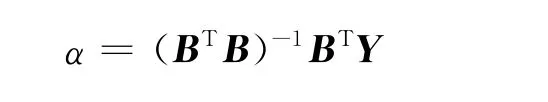
其中

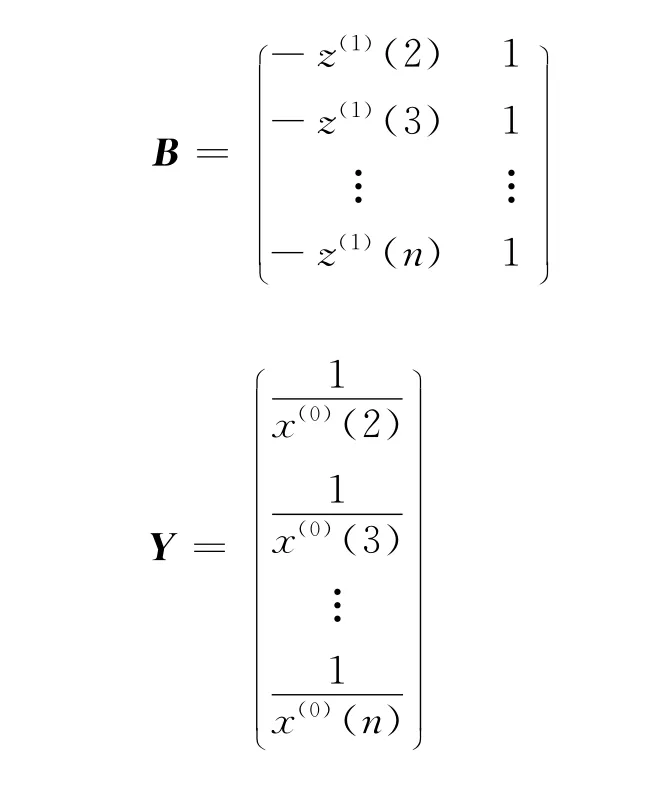
2）连续型响应函数为：

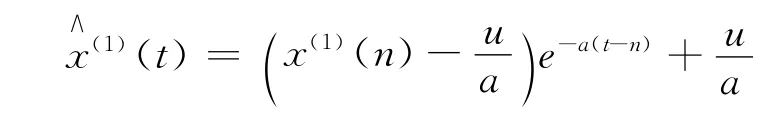
3）离散型响应函数为：

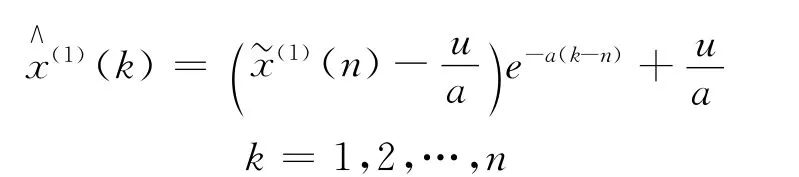
4）原始序列的模拟值为：

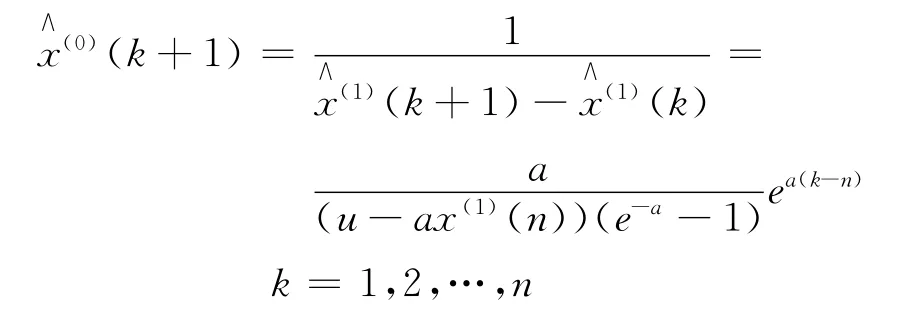
3 应用实例

文献［8］中给出了N2O5在热分解反应过程中，在等时间间隔里实验测得的分压数据为X（0）＝（24.7，18.5，14.0，10.5，7.8，5.8，4.4，3.3），这里温度T＝318.2K，单位为cmHg（1cmHg＝1 333.224Pa）。现仍然选取前6个数据建立优化GRM（1，1）模型，后2个数据作为预测检验。

由定理2求出α＝（－0.295 8，0.033 7），则得

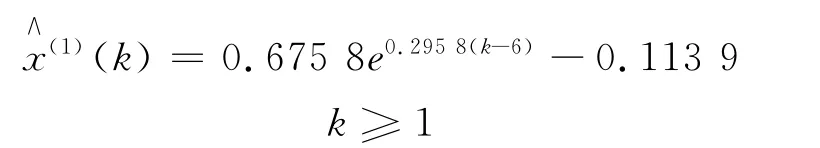
求出改进GRM（1，1）模型的模拟值和预测值，与文献［5］和［8］中得到的模拟值和预测值对比，见表1。

表1 模拟效果比较

其中

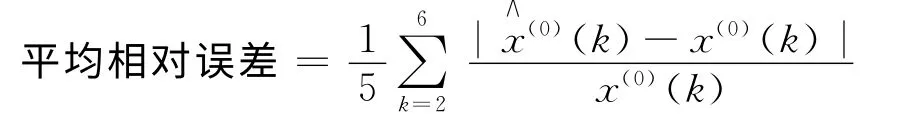
由表1可以看出，文中将X（1）的第n个分量x（1）（n）作为初始条件与优化背景值相结合的方法对GRM（1，1）模型进行改进，与文献［5］和［8］相比，提高了模型的模拟精度，而且计算方法较文献［8］简单。

4 结 语

改进的灰色GRM（1，1）模型在一定程度上消除了传统灰色模型在背景值获取和初始值选取时造成的误差，具有较高的模拟和预测精度，拓宽了适用范围。

［1］ 杨知，任鹏，党耀国.反向累加生成与灰色GOM（1，1）模型的优化［J］.系统工程理论与实践，2009，29（8）：161－162.

［2］ 孔新海，刘志斌，魏勇.单调递减序列的离散变换及其灰色建模［J］.统计与决策，2012（10）：19－21.

［3］ 杨保华，张忠泉.倒数累加生成灰色GRM（1，1）模型及应用［J］.数学的实践与认识，2003，33（10）：21－26.

［4］ 罗党，刘思峰，党耀国.灰色模型GM（1，1）优化［J］.中国工程科学，2003，8（5）：50－53.

［5］ 何霞，刘卫锋.灰色GRM（1，1）模型的改进及其应用［J］.江南大学学报：自然科学版，2011，10（3）：279－281.

［6］ Wang Z X，Dang Y G，Liu S F.Optimization of background value in GM（1，1）model［J］.Systems Engineering－Theory ＆Practice，2008，28（2）：61－67.

［7］ 党耀国，刘思峰，刘斌.以x（1）（n）为初始条件的GM模型［J］.中国管理科学，2005（1）：132－134.

［8］ 安燕，吴启勋.倒数累加生成灰色GRM（1，1）模型及其在化学动力上的应用［J］.计算机与应用化学，2006，23（2）：187－189.