一道浙江竞赛题引发的思考
沈小红 计惠方 (湖州市王勇强名师工作室 浙江湖州 313000)
一道浙江竞赛题引发的思考
沈小红 计惠方 (湖州市王勇强名师工作室 浙江湖州 313000)
2015年浙江省高中数学竞赛中有这样一道形式优美,入口平宽,解法众多,创意新颖,内涵丰富的好试题.
1)求椭圆C1的方程;
2)若直线l与曲线C1,C2都只有一个公共点,记直线l与圆C2的公共点为A,求点A的坐标.
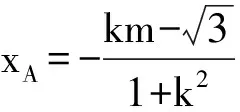
消去y得 (1+4k2)x2+8kmx+4m2-4=0,
从而
Δ1=16(4k2-m2+1)=0,
即 4k2-m2+1=0.
(1)
联立方程组
消去y得

从而

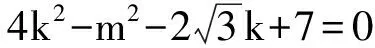
(2)
经检验A(0,2)或A(0,-2)符合题意,故所求点A的坐标为(0,2),(0,-2).


联立方程组
消去y得

令Δ=0解得


经检验A(0,2),或A(0,-2)符合题意,故所求点A的坐标为(0,2),(0,-2).
1 赛题的另解

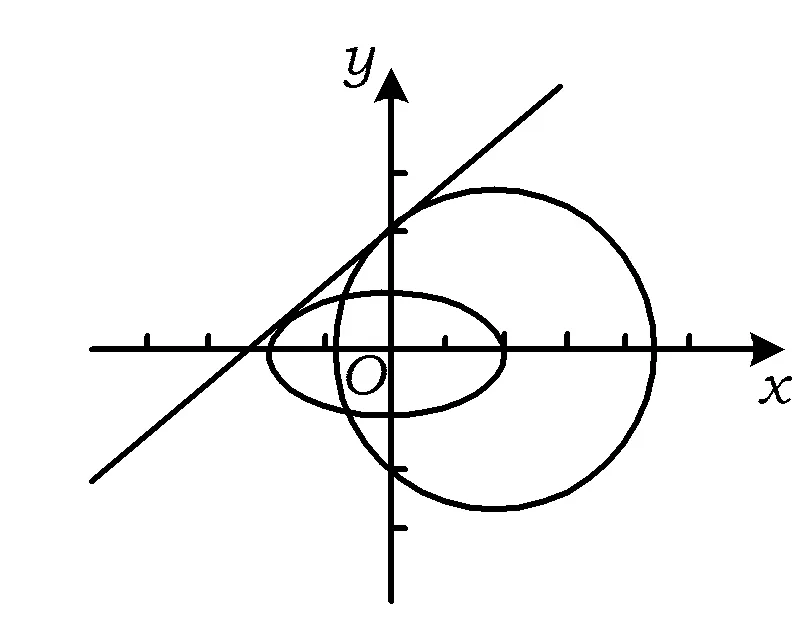
图1
经检验A(0,2)或A(0,-2)符合题意,故所求点A的坐标为(0,2),(0,-2).
2 赛题的推广
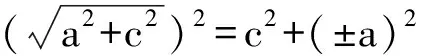
消去y得
(b2+a2e2)x2+2a3ex+a4-a2b2=0,
即
x2+2cx+c2=0,

证明 当公切线l的斜率不存在时,显然不满足题意.当公切线l的斜率存在时,可设直线l的方程为
y=mx+n(其中m,n∈R),
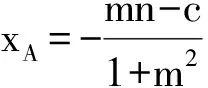
消去y得
(a2m2+b2)x2+2a2mnx+a2n2-a2b2=0,
(3)
从而
Δ1=4(a2m2-n2+b2)=0,
即a2m2-n2+b2=0.
(4)

消去y得
(1+m2)x2+2(mn-c)x+n2-a2=0,
从而
Δ2=4(a2m2+a2-2mnc+c2-n2)=0,
即a2m2+a2-2mnc+c2-n2=0.
(5)

a2m4+b2m2-c2=0,
即

故

因此曲线C1,C2的公切线有且仅有2条,其方程分别为
l1:y=ex+a和l2:y=-ex-a.
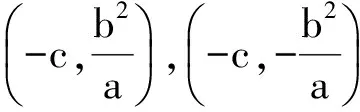
3 赛题的引申
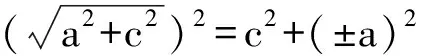
消去y得
(b2-a2e2)x2-2a3ex-a4-a2b2=0,
即
x2+2cx+c2=0,

证明同命题1′(略).
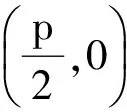
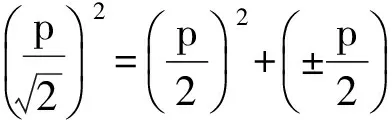
消去y得

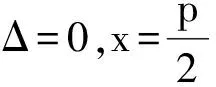
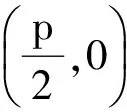
证明同命题1′(略).