以阿氏圆为背景编拟问题的新视角

余建国 (大厂高级中学 江苏南京 210044)



以阿氏圆为背景编拟问题的新视角

余建国 (大厂高级中学 江苏南京 210044)

阿波罗尼斯与阿基米德、欧几里德齐名，被称为亚历山大时期数学三巨匠．阿波罗尼斯对圆锥曲线有深刻而系统的研究，其主要研究成果集中在他的代表作《圆锥曲线》一书，阿波罗尼斯圆是其研究成果之一．

1 关于阿波罗尼斯圆

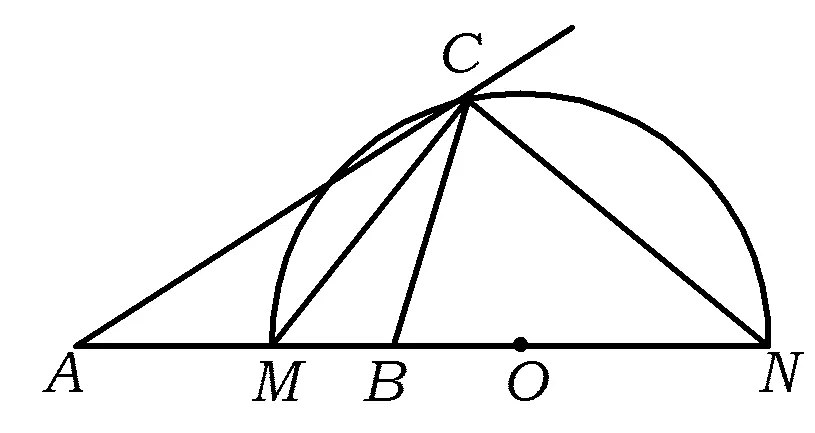
图1

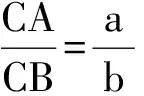
2 以阿氏圆为背景的问题回顾

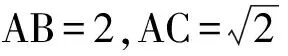
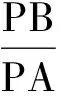
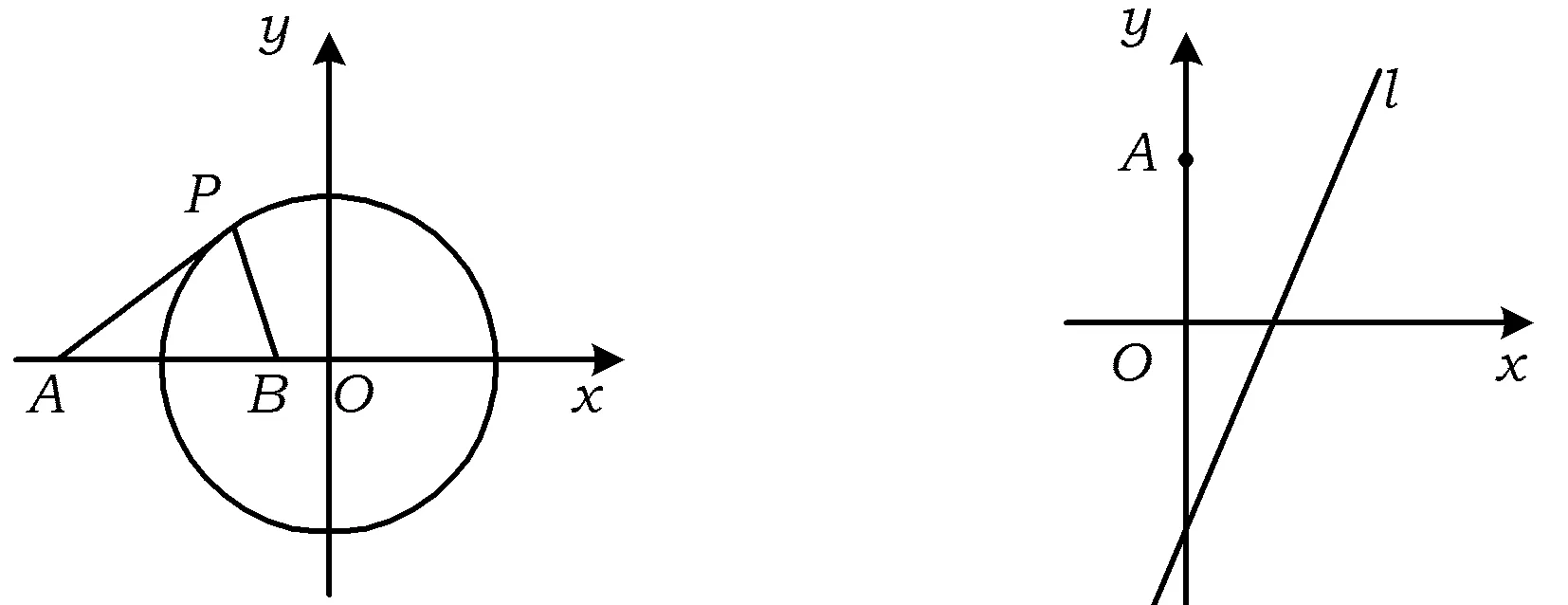
图2 图3

以上这些以阿氏圆为背景的问题，共同点都是“2个定点”是定的——无论是已知的，还是求出的．如2013年江苏省数学高考试题第17题：如图3，在平面直角坐标系xOy中，点A(0，3)，直线l：y=2x-4．设圆C的半径为1，圆心在l上，1)略；2)若圆C上存在点M，使MA=2MO，求圆心C的横坐标a的取值范围．将阿氏圆设为隐蔽的，并将这个圆与另一个动圆联系起来，通过2个圆的位置关系确定动圆中参数的取值范围．这个改编立意新颖，为继续设计以阿氏圆为背景的问题提供了新的视角．

3 以阿氏圆为背景编拟问题的新视角

视角1 直线与圆域的位置关系

设计方法 将阿氏圆定义中的“=”改为“>(或<)”，那么动点C的轨迹就变成了阿氏圆的外部(或内部，视比值大小而定)了，称这个轨迹为圆域,由此可以转而研究直线与圆域的位置关系，或者2个圆(域)的位置关系．

例1 已知点A(0，2)，B(1，0)，D(t，0)(其中t>0)，M是线段AD上的动点，若t是使AM≤2BM恒成立的最小正整数，则t=______．

解 设点M(x，y)，由AM≤2BM得

x2+(y-2)2≤4[(x-1)2+y2]，

化简得

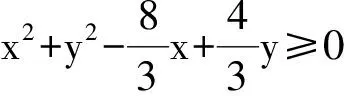
即

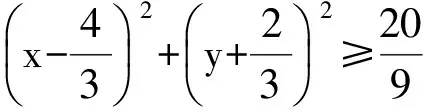
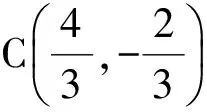
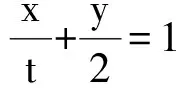
即

2x+ty-2t=0，

因此

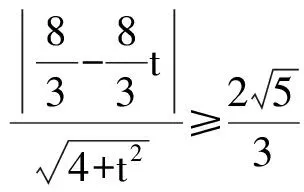
化简得

11t2-32t-4≥0．

因为t是正整数，且当t=1，2，3时，该不等式不成立，而当t=4时，该不等式成立，所以t=4．

视角2 一个定点在某直线上动起来

设计方法 阿氏圆中的2个定点是“固定不动”的，如果让其中一个在某直线上动起来，那么阿氏圆也随之改变位置，研究这个动圆与其他曲线的位置关系．

例2 已知圆C：(x-1)2+(y-4)2=4，若过x轴上的一点P(a，0)可以作一条射线，与圆C依次相交于点A，B，且PA=AB，求实数a的取值范围．

由点A，B均在圆C上，得

(1)

及

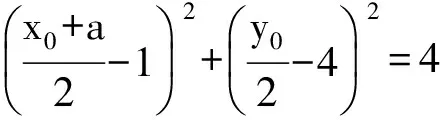
即 (x0+a-2)2+(y0-8)2=16.

(2)

式(1)和式(2)表明:圆C与圆D：(x+a-2)2+(y-8)2=16有公共点，从而

4-2≤CD≤4+2，

即

4≤(a-1)2+16≤36，

解得

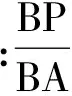
例3 已知△ABC的3个定点A(-1，0)，B(1，0)，C(3，2)，其外接圆的圆心为H.

1)若直线l过点C且被圆截得的弦长为2，求直线l的方程；

2)对于线段BH上的任意一点P，若在以点C为圆心的圆上都存在2个不同的点M，N，使得点M是线段PN的中点，求圆C的半径r的取值范围．

解 1)x=3或4x-3y-6=0．

由于点M，N都在半径为r的圆C上，从而

(3)

及

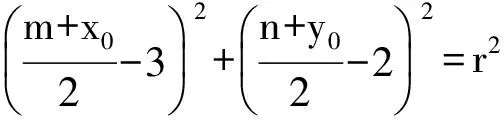
即 (x0+m-6)2+(y0+n-4)2=4r2.

(4)

式(3)和式(4)表明:圆C与圆D：(x+m-6)2+(y+n-4)2=16有公共点，从而

2r-r≤CD≤2r+r，

即

r2≤(m-3)2+(n-2)2≤9r2.

又3m+n-3=0，得

r2≤10m2-12m+10≤9r2,

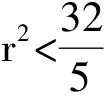
视角3 一个定点在某圆上动起来

设计方法 类似地，如果让其中一个“定点”在某圆上动起来，那么阿氏圆也随之改变位置，研究这个动圆与其他曲线的位置关系．

例4 在平面直角坐标系xOy中，圆C1：(x+1)2+(y-6)2=25，圆C2：(x-17)2+(y-30)2=r2．若圆C2上存在一点P，使得过点P可作一条射线与圆C1依次交于点A，B，满足PA=2AB，求半径r的取值范围．

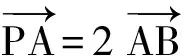
因为点A，B均在圆C1上，所以

(5)

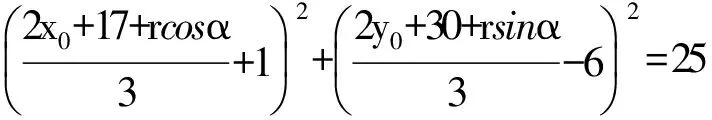
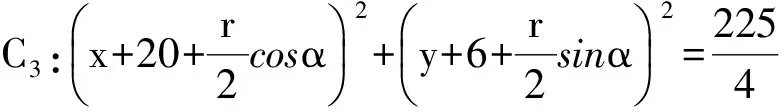
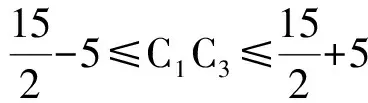
即关于α的不等式

有解．

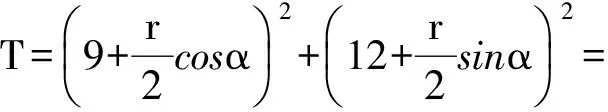
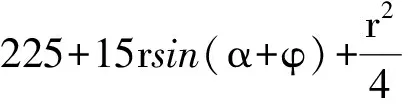
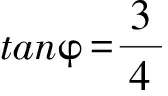
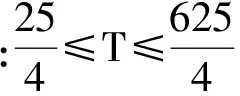
(7)

(8)

解式(7)得，5≤r≤55；式(8)恒成立．因此半径r的取值范围是[5，55]．

阿氏圆有多种表示形式，如运用复数形式可叙述为：满足

(9)

的复数z对应的点Z的集合就是阿波罗尼斯圆．式(9)可化为

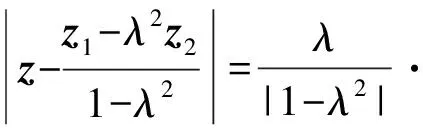
总之，像这样来源于数学史、数学定义的问题是我们取之不竭的宝库.如果在平时的教学中能够较多地渗透，不断地变换视角、改编挖掘，从“高观点”看数学问题，达到“居高临下”的境界，将更有利于提高习题的教学质量，培养学生的数学学习兴趣，促进学生创造思维的发展．

[1] 李锦旭．趣说阿波罗尼斯圆与高考[J]．中学生数学，2004(9)，32-33．

[2] 周永兴．从江苏08年高考13题的解法看“阿波罗尼斯圆”的应用[J]．数学通报，2009(5)，58-59．