某舰炮后坐力作用时间对动力放大系数影响研究

祝传超，张 龙，孙玉妹

（南京理工大学机械工程学院，江苏南京 210094）

某舰炮后坐力作用时间对动力放大系数影响研究

祝传超，张 龙，孙玉妹

（南京理工大学机械工程学院，江苏南京 210094）

0 引言

舰船在行进及舰炮发射过程中，系统会受到重力、后坐力和惯性摇摆力等作用。在基座及加强结构动力学分析中，需要通过动力放大系数来确定施加在系统的上水平力、竖直力及射击平面内的力矩。

对于不同舰炮，由于自身结构不同，后坐力增长持续作用时间及后坐力作用持续时间也有所不同。在系统阻尼一定的条件下，为探究后坐力作用时间对动力放大系数的影响，利用有限元软件，对舰炮基座及加强结构进行动力学分析和静力学分析，通过耳轴处的时间-位移曲线，探究动力放大系数在不同后坐力作用时间下的变化。

1 动力放大系数

火炮装置基座及加强结构是一个空间的连续弹性体，它的动力计算应按无限自由度弹性体系处理［1］。目前，对于这样的系统还没有有效的解决方法。为此，把火炮基座及加强结构简化为空间杆系，应用有限元法，将杆的质量分布到有限个节点上，这样就使其转化为有限个自由度的问题。

对于一般粘性阻尼的多自由度系统，在外激励的作用下，系统的微分方程为：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；F为外部激励向量。

对于外力是任随时间变化的激励，用振型叠加法［2］很容易算出各广义坐标的响应，即

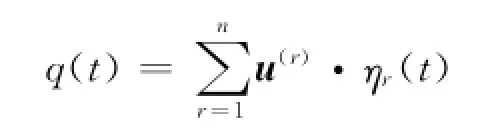
u为振型矩阵；η为正则坐标。

动力放大系数是μD是基础结构的固有频率ω、作用时间t和阻尼比ζ的函数［3］，即μD＝μ（ω1ω2…ωn，t，ζ）。它被定义为在相同载荷作用下动力位移响应与静力位移响应的关系［4］，即

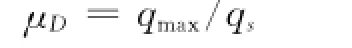
qmax为结构在动力计算下的最大位移；qs为相同载荷作用下结构的静位移。

对于舰炮，由GJB／Z 119－99水面舰艇结构设计计算方法查得动力放大系数：

τ为加强结构的自振周期；T1为后坐力增长持续时间。

2 舰炮后坐力简化

舰炮发射时作用于结构上的后坐力持续时间很短，一般只有几十至一百毫秒［5］，为探究动力放大系数在不同后坐力作用时间下的变化，并参照GJB／Z 119—99水面舰艇结构设计计算方法，在设计计算中，后坐力随时间变化一般可简化为图1的形式。

图1 后坐力简化一

图1中，Pmax为最大后坐力；T1为后坐力增长持续时间；T2为后坐力作用持续时间；T为后坐力作用总时间。

实验测得舰炮在方位角0°，俯仰角85°发射过程中，后坐力F随时间t变化如图2所示。由图2可知，后坐力在到达最大值的过程中经过2次增长，首先在一个极小的时间内增大到一定值，平稳变化一段时间后再一次增加到最大后坐力。为力求接近实际工况，参照上述国军标舰炮后坐力简化标准，将后坐力作用曲线简化为图3的形式。

图2 舰炮发射时后坐力变化曲线

图3 后坐力简化二

本工况下后坐力作用总时间T≈0.11 s，后坐力初始增长时间tOA≈0.003 s，极其短暂，因此可近似认为后坐力增长持续时间为tBC，后坐力作用持续时间为tOC。

3 基座及加强结构动力学分析

3.1 结构有限元模型

对于多数复杂的空间结构，一般是在三维绘图软件中作出实体图形，然后导入到有限元软件中进行分析，但对于导入的实体结构往往存在较多的错误，造成分析过程的不收敛。一般的，结构中一个方向的尺度（厚度）远小于其他方向的尺度（一般规定厚度小于典型整体结构尺寸的1／10），并忽略沿厚度方向的应力，可以采用壳单元进行模拟［6］。由于舰炮基座及加强结构基本是由板结构和梁结构组成，且板梁厚度远小于其他方向尺度，因此可在ABAQUS中直接采用壳单元建模，材料弹性模量为206 GPa，泊松比为0.3，结构模型如图4所示。

图4 基座及加强结构有限元模型

3.2 后坐力的施加

本工况选取方位角0°，俯仰角85°，后坐力分解为FX、FY、FZ，施加于耳轴处，并考虑后坐重心移动的影响，引入力矩MX，MY，如图4。按图3，建立10种后坐力幅值曲线，即有：

a.T1＝0.02 s，T2分别取0.04 s、0.05 s、0.06 s、0.07 s、0.08 s。

b.T2＝0.08 s，T1分别取0.02 s、0.03 s、0.04 s、0.05 s、0.06 s。

3.3 计算结果分析3.3.1 静力学分析

在ABAQUS Standard模块中，将后坐力以一定的幅值增加到最大值施加到模型耳轴处，得到模型耳轴处静力作用下时间-位移变化曲线如图5所示。

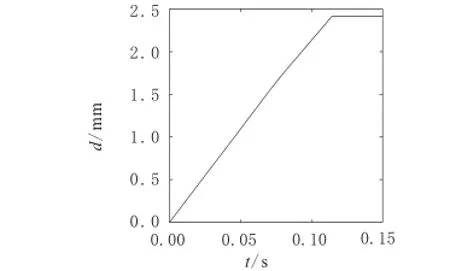
图5 耳轴处静力位移变化曲线

得到耳轴处最大静位移qs＝2.41。

3.3.2 动力学分析

对上述10种后坐力幅值曲线分10种工况进行动力学分析。

T2固定改变T1，耳轴处的时间-位移曲线如图6所示。

图6 T2固定时耳轴处位移变化曲线

由图6可知：

a.在舰炮发射初始阶段，不同后坐力增长持续时间下的时间-位移曲线相同，这是因为在0～0.0阶段，各工况下所受载荷相同。

b.0.03 s之后，由于后坐力幅值发生变化，各工况下的曲线形状开始改变，主要体现在各工况下耳轴处的位移曲线幅值不同。根据仿真数据，将各工况下位移幅值qmax及相应动力放大系数列于表1中。

表1 不同T1时耳轴处位移幅值及动力放大系数

c.后坐力增长持续时间越长，载荷变化越平缓，位移曲线幅值越小，动载荷系数越小；即T1越大，动载荷系数越小，与公式K＝1＋τ／（π·T1）反映规律一致。

T1固定改变T2，耳轴处的时间-位移曲线如图7所示。

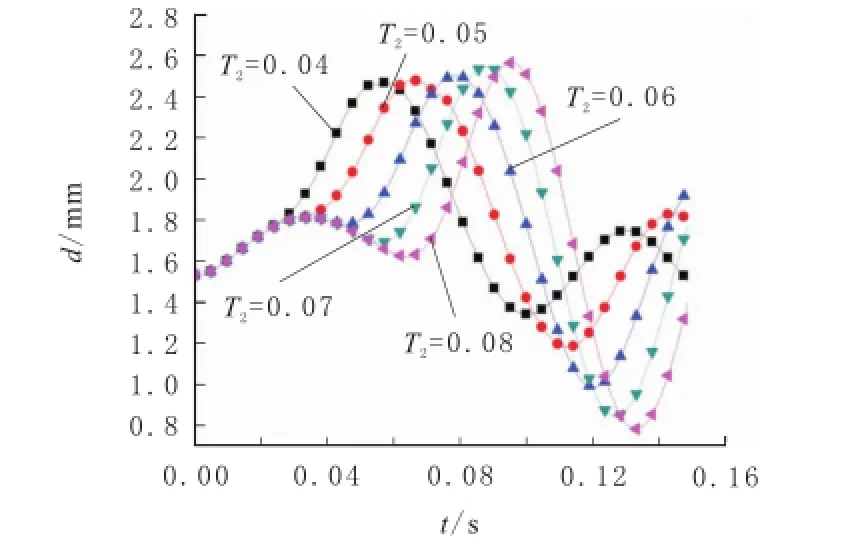
图7 T1固定时耳轴处位移变化曲线

由图7可知：

a.各工况下耳轴处位移曲线到达峰值的时间不同，这是由于后坐力作用持续时间改变，导致后坐力到达峰值的时间不同而引起。

b.各工况下耳轴处的位移曲线幅值不同。根据仿真数据，将各工况下位移幅值及相应动力放大系数列于表2中。

c.后坐力作用持续时间越长，位移曲线幅值越大，动载荷系数越大；即T2越大，动载荷系数越大。

表2 不同T2时耳轴处位移幅值及动力放大系数

4 结束语

通过对某舰炮基座及加强结构静力学及动力学仿真，得到在不同后坐力增长持续时间和后坐力作用持续时间下的耳轴处位移曲线，继而得到在确定后坐力的作用下系统的动力放大系数，并由此得到如下结论：

a.在一般计算中动力放大系数K取2，取值虽然相对保守但却也有效。

b.动载荷系数既与后坐力增长持续时间相关，又与后坐力作用持续时间相关。因此，建议综合考虑2种时间（后坐力增长持续时间和后坐力作用持续时间）进行动力放大系数的计算。动力放大系数与二者的具体关系式还需大量的研究计算。

［1］ 宋文瀚，杨鸿新.用子空间迭代法求解舰艇火炮装置加强结构自由度振动及程序［J］.海工科技，1981（2）：1-10.

［2］ 胡少伟，苗同臣.结构振动理论及其应用［M］.北京：中国建筑工业出版社，2005.

［3］ 廖小军.船舶侧向撞击桥梁基础的动力放大系数探讨［J］.公路交通术，2009（2）：78-82.

［4］ 蔡建国，朱奕锋，江超，等.基于应力比值法的张弦结构动力放大系数研究［J］.建筑结构学报，2015，36（1）：116-126.

［5］ 杨鸿新，王裕玮，宋文瀚.火炮发射率对舰艇结构动力学响应的影响［J］.海军工程学院学报，1983（3）：13-23.

［6］ 庄茁，由小川，廖建晖，等.基于ABAQUS的有限元分析与应用［M］.北京：清华大学出版社，2009.

Study on the Influence of a Naval Gun’s Recoil Action Time on Dynamic Magnification Coefficient

ZHU Chuanchao，ZHANG Long，SUN Yumei
（School of Mechanical Engineering，Nanjing University of Science and Technology，Nanjing 210094，China）

为保证舰炮发射安全，需对舰炮基座及加强结构进行强度校核，而动力放大系数是校核中不可或缺的元素。以ABAQUS为基本工具，以改变后坐力增长持续作用时间及后坐力作用持续时间为基本方法，分析研究了舰炮在极限工况下不同后坐力作用时间对动力放大系数的影响，基于仿真结果提出了校核过程中部分改进方法。

舰炮；动力放大系数；后坐力

In order to ensure the safety of naval guns，strength checks must be performed on the base and reinforcement structure，and the dynamic magnification coefficient is an essential element in the check.Based on ABAQUS，by changing the recoil growth duration and recoil duration of action as the basic method，the impact of recoil action time on the dynamic magnification coefficient in extreme conditions is analyzed，and suggestions for improvement on some of the strength check procedures are proposed based on simulation results.

naval gun；dynamic magnification coefficient；recoil

TJ391

A

1001-2257（2015）09-0024-03

祝传超（1988－），男，山东菏泽人，硕士研究生，研究方向为舰载武器结构动力学。

2015-06-18