扩展不确定度评定中包含因子的确定探讨

范巧成 姜文娟 郑磊

(1.山东电力研究院，济南 250003；2.国网技术学院，济南 250002)



扩展不确定度评定中包含因子的确定探讨

范巧成1姜文娟2郑磊1

(1.山东电力研究院，济南 250003；2.国网技术学院，济南 250002)

指出了扩展不确定度评定中包含因子的确定存在的问题，探讨根据输入量的分布如何确定输出量的分布，进而给出扩展不确定度评定中包含因子的确定原则，达到一般应用时简化评定的目的，这种确定原则既适合于校准也适合于检测工作的测量不确定度评定。

不确定度评定；扩展不确定度；分布估计；包含因子

0 引言

在JJF 1059—1999实施初期，中国计量出版社出版了一些有关测量不确定度评定的专著[1～3]，在杂志中也发表了一些论文，这些评定实例几乎一律采用计算有效自由度的方法来确定计算扩展不确定度的包含因子k95或k99，这无疑增加了许多计算工作量。这里有两个问题，一是只有当输出量的分布接近正态分布即t分布时，才可以通过计算有效自由度来获取k95；二是当输出量的分布为其它已知的分布时，不存在计算自由度的问题。例如输出量的分布为均匀分布，则k95=1.65，k99=1.71，这在文献[4-5]中都有明确规定。还有一种处理方式是不管输出量的分布如何，直接取k=2，这在输出量为均匀分布时也是不妥的。文献[5-6]中有对自由度弱化处理的规定，即当输出量的分布接近正态分布时，可以不必计算有效自由度，在估计其值不算小的情况下可以直接取k=2，此时对应的包含概率约为95%。这里就梳理一下，对于一般应用，计算扩展不确定度的包含因子应如何选取比较合理。

1 输出量与输入量分布的估计

1.1 输入量分布的估计

在B类评定中，分布的估计确实是一个不好确定的问题，尤其是对于初学者。但是，这一问题又不能回避，它将影响到输出量分布的估计，进而影响到评定扩展不确定度时包含因子的确定。分布估计的大致原则为，在缺乏任何其它信息的情况下，一般估计为矩形分布是较合理的。但如果已知被研究的量Xi的可能值出现在a-～a+中心附近的概率，大于接近区间的边界时，则最好估计为三角分布；如果已知被研究的量Xi的可能值出现在a-～a+中心附近的概率，小于接近区间的边界时，则最好估计为反正弦分布。在实际工作中，可根据同行专家的研究结果或经验来假设概率分布[5]。

估计为均匀分布和正态分布是最多的。估计为均匀分布的有：按级使用的测量仪器最大允许误差、数据修约、数字式测量仪器对示值量化、度盘或齿轮的回差、平衡指示器调零不准、测量仪器的滞后或摩擦效应导致的不确定度。估计为正态分布的有：部分按级使用的测量仪器、已知级别的装置，其最大允许误差导致的不确定度，如标准电能表、电能表检定装置；校准证书中给出的U或Up未指明分布时按正态分布。

按级使用的测量仪器最大允许误差导致的不确定度，很多人通常都是估计为均匀分布，其实不然，具体估计为何种分布，需要对该类仪器的示值误差做大量的统计工作才能得到。例如标准电能表的误差分布规律，通过大量检定数据统计，认为其示值误差接近正态分布[7-8]，如图1(0.1级表、400只、7254个数据)和图2(0.05级表、200只、5978个数据)。

图1 0.1级表误差分布图

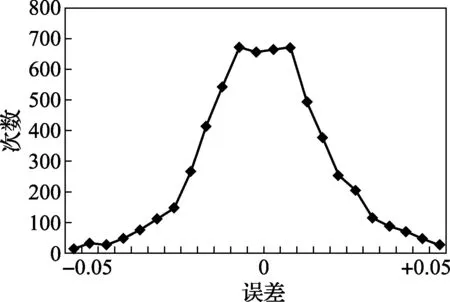
图2 0.05级表误差分布图

笔者还做过直流电阻箱、直流标准电阻、直流高压高阻箱、0.01级电流互感器比差和角差、0.05级电流互感器比差和角差的实测误差分布特征，由于统计样本较少，其分布曲线没有像图1那样接近正态分布，但大致接近，表现为中间多两边少，呈现凸型，两边接近最大允许误差的很少。其它测量仪器的误差分布规律，感兴趣并有条件的读者可作一下统计，其结论可与大家分享。

按级使用的测量仪器其最大允许误差导致的不确定度，在没有足够的证据表明其接近何种分布时，从保守的角度考虑估计为均匀分布是比较合理的。

1.2 输出量分布的估计

文献[9]提出了被测量可能值的分布及其判定方法，提供的实例在评定扩展不确定度前，首先根据输入量标准不确定度分量的分布来确定输出量的分布，文献[10]也参照文献[9]做了类似的处理。输出量的分布大致有如下几种情况。

1.2.1 输出量的分布为均匀分布

出现这种情况的原因是只有一个分量是占绝对优势(其它分量为该分量的1/3以下)的分量，其它分量可以忽略不计，该分量被估计为均匀分布，则输出量的分布估计为均匀分布。

1.2.2 输出量的分布为梯形分布

出现这种情况的原因是只有一个分量是占绝对优势(其它分量为该分量的1/3以下)的分量，其它分量可以忽略不计，该分量被估计为梯形分布，则输出量的分布估计为梯形分布。或者存在两个主要分量为不等宽的均匀分布，则输出量的分布估计为梯形分布。

1.2.3 输出量的分布为三角分布

出现这种情况的原因是只有一个分量是占绝对优势(其它分量为该分量的1/3以下)的分量，其它分量可以忽略不计，该分量被估计为三角分布，则输出量的分布估计为三角分布。或者存在两个主要分量为等宽的均匀分布，则输出量的分布估计为三角分布。

1.2.4 输出量的分布接近正态分布

出现上述三种情况以外的情况时，输出量的分布可估计为接近正态分布[11]，主要表现为：

1)被测量Y的合成标准不确定度uc(y)中，相互独立的分量ui(y)较多，它们之间的大小也比较接近时；

2)被测量Y的合成标准不确定度uc(y)中相互独立的分量ui(y)中，存在两个界限值接近的三角分布，或四个界限值接近的均匀分布时；

3)被测量Y的合成标准不确定度uc(y)相互独立的分量ui(y)中，量值较大的分量(起决定作用的分量)接近正态分布时。

2 扩展不确定度评定中包含因子的确定

2.1 输出量不同分布对应包含因子的确定

有了上述对输出量的分布估计，根据给定的包含概率来确定评定扩展不确定度的包含因子。根据输出量的分布大致有如下几种情况。

2.1.1 输出量的分布为均匀分布

取k95=1.65，k99=1.71，k100=1.73[5]。此时如果取k=2会使扩展不确定度U95明显增大，而且超出了均匀分布的半宽a，因为u=a/1.73，则U=2×u=2×a/1.73=1.16a，这就有点不合理了。

2.1.2 输出量的分布为梯形分布

根据角参数β值(β为两均匀分布半宽的差与其和的比值，若β=0，则梯形分布成为三角分布；若β=1，梯形分布成为矩形分布)来确定包含因子k，如表1。分析这些β值，当β=0.5时，一个均匀分布的半宽正好是另一个的1/3，当β>0.5时，一个均匀分布的半宽小于另一个的1/3，这符合1.2.1的情况，输出量的分布可近似看作均匀分布。当β<0.5时，k95=1.81～1.90，k99=2.07～2.20，此时取包含因子k=2会使扩展不确定度U95增大约10%，但从保守的角度是可以接受的，此时取k=2，对应的包含概率应在95%～99%之间。

表1 被测量接近于矩形分布、三角分布和梯形分布时的包含因子

2.1.3 输出量的分布为三角分布

三角分布是β=0的梯形分布，k95=1.9，k99=2.2，此时取包含因子k=2会使扩展不确定度U95增大约5%，这从保守的角度是完全可以接受的。取k=2，对应的包含概率在95%～99%之间。

2.1.4 输出量的分布接近正态分布

在此情况下可不必计算有效自由度，直接取包含因子k=2，其对应的包含概率约为95%。实际上，对于校准来说，往往已把主要分量的自由度估计为50，这样计算得到的有效自由度也将为50左右，查t分布表得k95≈2。文献[1-3]提供的许多实例就是这样。

2.2 包含因子的确定

综上所述，根据输出量的分布情况，可归纳为：

输出量的分布为均匀分布，则k95=1.65，k99=1.71。

输出量的分布为梯形分布，当β≥0.5时，输出量的分布可近似看作均匀分布；当β<0.5时(含三角分布)，取k=2，对应的包含概率在95%～99%之间。

输出量的分布接近正态分布，直接取包含因子k=2，其对应的包含概率约为95%。对于检测领域，一般直接取包含因子k=2[12-13]。

更为简约的处理：输出量的分布为均分布，则k95=1.65，k99=1.71；其它情况直接取包含因子k=2。这对于一般的应用是可以接受的，对于输出量的分布为梯形分布的，可省去了角参数β值的计算，对于输出量的分布为接近正态分布的，可省去了自由度的计算。

3 结束语

通过对部分专著[1-3]和一些论文的不确定度评定分析，结合文献[5-6]中有关对自由度弱化处理的规定，参考文献[9]提出的被测量可能值的分布及其判定方法，根据输入量标准不确定度分量的分布来确定输出量的分布大致可分为四种：均匀分布、梯形分布、三角分布和接近正态分布。根据这四种分布情况，总结得出扩展不确定度评定中包含因子的确定：输出量的分布为均分布，则k95=1.65，k99=1.71；其它情况可直接取包含因子k=2。这对于一般的应用是可以接受的，对于输出量的分布为梯形分布的，可省去了角参数β值的计算；对于输出量的分布为接近正态分布的，可省去了自由度的计算。这种处理简化了评定过程，将有利于测量不确定度的评定与应用。

[1] 全国计量标准、计量检定人员考核委员会组编.测量不确定度评定与表示实例[M].北京：中国计量出版社，2001

[2] 上海市计量测试技术研究院编著.常用测量不确定度评定方法及应用实例[M].北京：中国计量出版社，2001

[3] 宣安东,等.实用测量不确定度评定及案例[M].北京：中国计量出版社，2007

[4] 国家质量技术监督局.测量不确定度评定与表示(JJF 1059—1999).北京：中国计量出版社，1999

[5] 国家质量监督检验检疫总局.测量不确定度评定与表示(JJF 1059.1—2012).北京：中国质检出版社，2012

[6] 国家质量监督检验检疫总局.计量标准考核规范(JJF 1033—2008).北京：中国计量出版社，2008

[7] 范巧成.电能表示值误差测量结果的不确定度评定问题商榷[J].计量技术，2010(12)

[8] 范巧成，等.校准结果测量不确定度评定问题商讨[J].电测与仪表，2011(12)

[9] 倪育才.实用测量不确定度评定(第3版)[M].北京：中国计量出版社，2009

[10] 范巧成，等.Excel在测量不确定度评定中的应用及实例[M].北京：中国质检出版社，2013

[11] 范巧成，等.三相三线电能计量装置综合误差的不确定度评定[J].计量技术，2012(1)

[12] 郭兰典，等.商品检测不确定度评定释例[M].北京：中国计量出版社，2004

[13] 承忠，等.材料理化检验测量不确定度评估指南及实例[M].北京：中国计量出版社，2007

10.3969/j.issn.1000-0771.2015.08.22