液体模塑成型工艺中纤维束横向渗透率的细观数值模拟
李永静, 晏石林, 李德权, 严 飞
(武汉理工大学 理学院, 湖北 武汉 430070)
液体模塑成型工艺中纤维束横向渗透率的细观数值模拟
李永静, 晏石林, 李德权, 严 飞
(武汉理工大学 理学院, 湖北 武汉 430070)
将纤维束视为多孔介质,基于达西定律,对纤维束横向渗透率进行细观数值模拟研究。首先建立了纤维束横截面单丝规则及随机分布的细观数值分析模型,在给定压力梯度下实现了对纤维束横向渗透率系数的数值预报;其次研究了纤维束内孔隙率不变时,模型尺寸对渗透率计算结果的影响,分析了计算模型的尺寸效应,确定了纤维束横向渗透率计算的最小细观数值模型尺寸;最后进行了不同孔隙率下单丝随机分布的纤维束横向渗透率数值分析,得到了孔隙率对横向渗透率的影响规律,并与建立在单丝规则排列基础上的Gebart模型和Cell模型做对比。
液体模塑成型; 横向渗透率; 数值模拟; 数据拟合
树脂基复合材料由于质量轻、耐腐蚀、绝缘性好及良好的力学性能被广泛应用于航空航天、化工、电子、汽车及建筑等领域[1-2]。液体模塑成型(LCM)是高性能复合材料的低成本制备技术,其技术关键是在不影响已铺放好的增强材料,模具不承受过大压力的前提下,实现树脂对模具腔内增强材料的完全浸渍,并尽可能排除所有空气[3-4]。要达到上述目的,需合理控制填充过程中的工艺参数,如注射压力、流动速率、树脂黏度及纤维预制件的渗透率等,其中纤维预制件的渗透率及其影响因素是控制LCM工艺制品质量的关键。在LCM工艺中,纤维预制件一般由纤维束编织或缝合而成,树脂在纤维预制件中的浸润流动包括纤维束内的微观流动及纤维束间的宏观流动。纤维预制件的渗透率不仅取决于纤维束间的宏观流动,而且与纤维束内的微观渗透性密切相关。为得到树脂在纤维预制件中的渗透情况,可采用实验、数值计算等方法。蒋金华等[5]采用超声波监测技术研究了不同结构织物的内部流动行为及渗透差异性。实验方法虽能很好地再现实际工况,但实验周期长,成本高,采用数值计算可显著缩短实验周期及研发成本。在对纤维预制件的渗透率进行数值计算时,一种观点是将纤维束视为不可浸润的实体,如陆振乾等[6]利用分形原理推导得出了纤维织物渗透率的理论计算公式。另一种则将纤维束视为带有微观孔隙的可浸润多孔介质。根据预制件中纤维束的周期性结构,先建立包含纤维束及纤维束间缝隙的三维单胞模型,并将纤维束视为渗透率已知的管束,模拟树脂在单胞中的流场特性,再基于达西定律得到单胞(或纤维预制件)的宏观等效渗透率[7-9]。在对单胞进行数值模拟计算中,赋予纤维束的渗透率大都是通过Gebart[10-11]或Cell[11-12]等模型的理论公式计算得到的,而这些理论公式基于纤维束横截面内纤维单丝规则排列的假设,与纤维束内纤维单丝随机分布的实际情况并不相符,且Gebart模型计算结果仅适用于孔隙率小于40%的情况,在孔隙率为40%的中间区域,Gebart和Cell模型计算所得的渗透率数值相差较大。纤维束渗透率的数值模拟计算方面,CAI等13]运用改进的自洽方法估算了沿纤维束轴向及横向的渗透率。BECHTOLD等[14]运用CFD实现了纤维束瞬态浸润的数值模拟,研究了纤维单丝的分布特性对微观尺寸内渗透率的影响。CHEN等[15]采用了蒙特卡洛法实现了纤维束内纤维单丝随机分散模型的建立,并运用边界单元法的并行计算实现了单向排列纤维束横向流动行为的数值模拟,考察了纤维单丝的分散性对渗透率的影响。赵艳娜等[16-17]实现了三角形和圆形纤维模型浸润流动的数值模拟及不同纤维体积分数下不同纤维单丝分布状态的纤维束横向流动数值模拟,研究了纤维单丝截面形状及纤维束微观结构对纤维束横向渗透率的影响。但是上述研究并未系统地讨论计算模型的大小对纤维束横向渗透率的数值的影响,因此,本文根据纤维束横截面内纤维单丝随机排列分布特征,建立模拟纤维束横向渗透率的细观数值分析模型,实现对纤维束横向渗透率的数值预报,探寻细观数值计算模型及纤维束内孔隙率对横向渗透率的影响规律,并与现有近似理论公式计算结果进行比较,验证其适用性。
1 计算模型的建立与数值模拟的实现
渗透率描述了预成型体对树脂流动的阻碍作用,是材料的固有属性。渗透率值的大小直接影响工艺的填充时间和树脂对纤维预制件的浸润方式,也是数值模拟方法用于模具设计、控制进出口位置及进口压力大小的关键因素之一。对于其数值计算的理论分析模型主要有毛细管模型和规则排列柱状模型。其中毛细管模型主要针对单向纤维,模型较为简单,模型中的争议焦点是Kozeny常数的取值问题。规则排列柱状模型将纤维多孔材料中的纤维单丝视为规则排列的柱,当孔隙率较低时采用近似润滑法(其代表性模型为Gebart模型),孔隙率较高时采用细胞模型,本文分别将数值模拟计算结果与规则排列柱状模型下的Gebart模型与细胞Cell模型(如表1所示)作对比,分析模拟结果的准确性。表中:ε为纤维束内的孔隙率,%;Vf为纤维束内纤维的实际体积分数,%;R为纤维单丝的半径,m;Vfmax为纤维束中纤维的最大体积分数,%;C1为系数。

表1 渗透率理论分析模型Tab.1 Theoretical analysis models of permeability
有限元通用商业软件中的流体动力学分析模块ANSYS/FLOTRAN可用于求解计算单相黏性流体的二维和三维流动。采用FLOTRAN进行数值模拟时,假定树脂对预制件的浸润过程为不可压缩流体对多孔介质的流动问题,并采用达西定律,可得到渗透率的计算式[2]为:
(1)

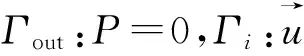

图1 玻璃纤维束截面扫描电镜照片(×100)Fig.1 SEM image of glass fiber bundle(×100)

图2 随机分布模型及边界示意图Fig.2 Randomly distributed model and boundary conditions
2 数值模拟结果与讨论
2.1 计算模型的尺寸效应
精确的数值模拟结果依赖于计算模型的准确建立。模拟纤维束横向渗透率时,需考察计算模型的尺寸效应,即确定模型中包含的纤维单丝数目。为区分随机分布效应和纤维单丝数目对计算结果的影响,需先考察纤维束内纤维单丝规则排列下横向渗透率随纤维单丝数目的变化。在相同孔隙率下,分别建立了纤维单丝数目N从9~289变化的有限元模型,模型中纤维单丝半径及纤维单丝间距离保持不变,如图3 (以孔隙率为45%为例)所示,计算模拟获得其在规则排列分布下的平均渗透率及其无量纲化值K/R2(R为纤维丝半径,本文取值为7.5×10-6m),其结果如图4所示。

图3 纤维单丝数目不同的纤维束计算模型Fig.3 Models with different numbers of fibers under same porosity
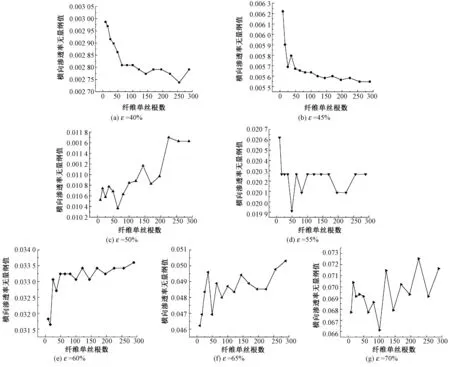
图4 孔隙率一定时无量纲渗透率值随纤维单丝数目变化Fig.4 Curve of dimensionless permeability with fiber number under same porosity
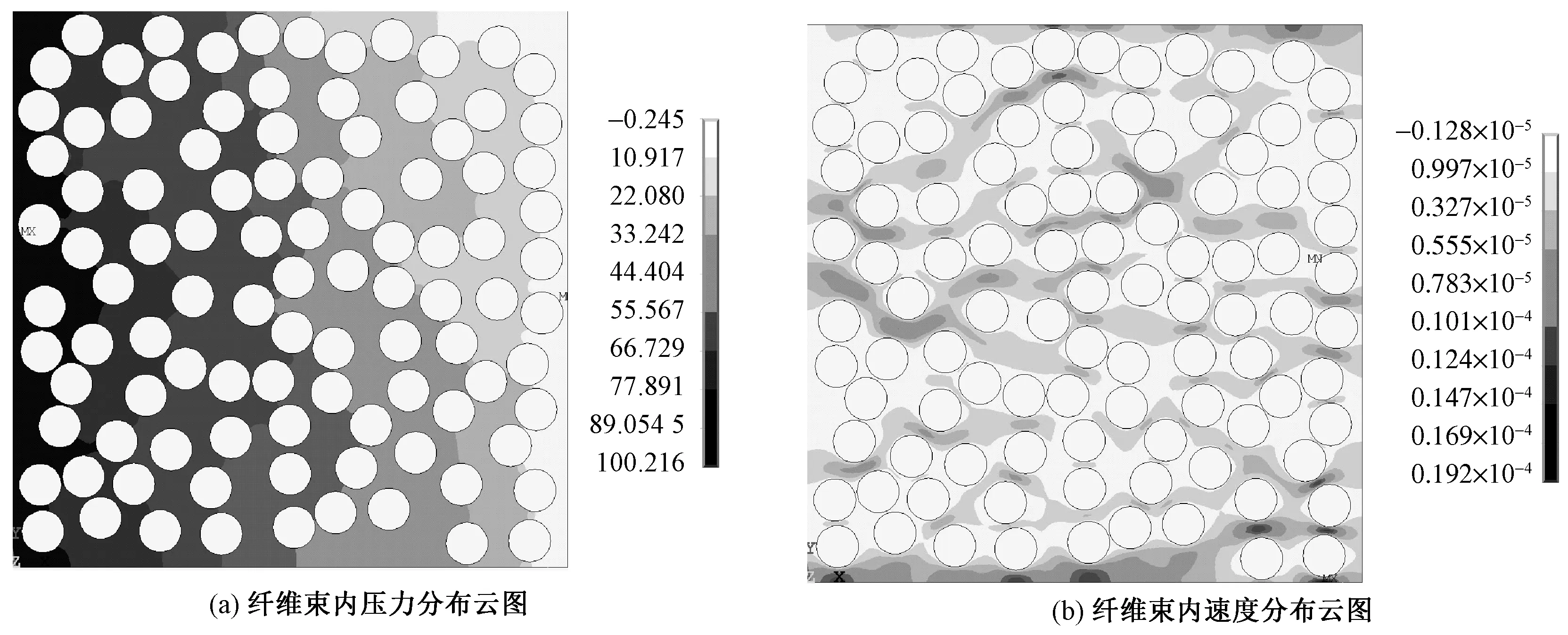
图5 随机分布模型下纤维束横截面内压力及速度分布云图Fig.5 Distributions of pressure and velocity of fiber bundle under randomly distributed model.(a) Distribution of pressure of fiber bundle; (b) Distribution of velocity of fiber bundle
由图可知,在相同孔隙率下,纤维束横向渗透率数值随纤维单丝数目的增多而出现一定的波动:在孔隙率较小时,该种波动随纤维单丝数目的增大而逐渐趋于稳定,当纤维单丝数目超过150~250时,该波动逐渐变小,渗透率数值逐渐趋于稳定;而在纤维束内孔隙率较大时,该种波动表现出非规则性。
为考察纤维束内纤维单丝随机分散性对纤维束横向渗透率数值的影响,本文实现了纤维束内孔隙率为55%时纤维束浸润的数值模拟,并分析了纤维束内压力及速度分布云图,如图5所示。
由纤维束横截面内的压力及速度分布云图可知,纤维单丝在纤维束内的分散性会影响纤维束内的压力及速度分布,进而影响纤维束的横向渗透率,因此,数据处理时为消除随机分布对渗透率值分散性的影响,相同孔隙率及压力条件下,可对随机生成的20个模型的渗透率值取平均作为纤维束横向渗透率的最终值。基于上述思想,在孔隙率一定时,保持纤维束内纤维单丝半径及单丝间的最小距离不变,本文考察了纤维束内孔隙率分别为70%、65%、60%时纤维束横向渗透率的无量纲值随纤维单丝数目的变化曲线,如图6所示。由图可知,在较大孔隙率下,纤维单丝数目大于150时,其渗透率逐渐趋于稳定。综合考虑规则分布及随机分布下纤维束渗透率随纤维单丝数目的变化规律,在利用数值模拟方法计算纤维束的横向渗透率时,纤维束有限元模型中纤维单丝的数目不应低于150根。

图6 不同孔隙率条件下无量纲渗透率值随纤维丝数目变化曲线Fig.6 Change of dimensionless permeability withfiber number at different porosities
2.2 孔隙率对横向渗透率的影响
基于上述分析结果,采用FLOTRAN模块计算纤维束横向渗透率时,模型中纤维单丝数目取为225根,纤维束内孔隙率为25%~60%,计算结果如图7所示。分析表明纤维束横向渗透率随纤维束内孔隙率的增大而增大。对计算结果进行数据拟合,可得到纤维束横向渗透率与孔隙率的关系为验证上述拟合公式的准确性,本文分别采用拟合公式、Gebart模型和Cell模型理论计算纤维束内孔隙率从15%到85%变化时无量纲横向渗透率值,如图8所示。结果表明,数值计算拟合结果与Gebart及Cell理论模型计算所得纤维束横向渗透率的变化趋势相同,且在孔隙率较小时,三者计算结果相差无几,当孔隙率增大时,其与Gebart模型结果误差较大,与Cell模型计算结果误差较小。这是由于Gebart模型及Cell模型理论计算公式的提出是基于纤维束内纤维单丝为规则排列柱状的假设,在孔隙率较低时,这一假设与纤维束内纤维单丝的实际排列较接近,因此3种方法计算所得到的纤维束横向渗透率值相差较小;当孔隙率较高时,这一假设与纤维束内纤维单丝的实际排列方式存在较大差异,而数值模拟中的随机模型很好地反映了纤维单丝的排列方式,其计算结果更加准确,因此,该数值模拟方法可用来准确估算纤维束的横向渗透率。
K/R2=0.000 162 08eε/0.083+0.000 205 9

图7 不同孔隙率下的无量纲横向渗透率值Fig.7 Dimensionless permeability at different porosities

图8 拟合曲线与不同计算结果对比图Fig.8 Comparison of fitting curve and different calculation methods′results
3 结 论
本文将纤维束视为多孔介质,建立了纤维束内纤维单丝的随机分布模型,并借助达西定律在给定压力梯度下实现了对纤维束横向渗透率值的数值模拟研究,分析了计算模型尺寸(计算模型内纤维单丝的数目)及纤维束内孔隙率对其渗透率的影响。结果表明:相同孔隙率下,保持纤维单丝半径及纤维单丝间最小距离不变时,纤维束的横向渗透率随纤维单丝数目的增大存在一定的波动,并最终逐渐趋于稳定,实际运用中,计算模型中纤维单丝的数目不应低于150;纤维束的横向渗透率受纤维束内纤维单丝分散性影响,且其数值大小随纤维束内孔隙率的增大而增大,采用FLOTRAN模块数值模拟计算时,可获得相同的变化规律,与Gebart及Cell模型相比结果表明,文中的数值模拟方法结果较准确,即FLOTRAN可用来计算纤维束的横向渗透率。通过对计算结果进行数据拟合,获得了纤维束横向渗透率随孔隙率连续变化的函数关系,工程实际应用中,一定的误差范围内可直接应用文中公式计算纤维束的横向渗透率。
[1] 赵渠森. 先进战斗机用复合材料树脂基体[J].高科技纤维与应用,2000,25(6):14-18. ZHAO Qusen. Resin matrix of composite for advanced military aircraft[J]. Hi-Tech Fiber & Application, 2000,25(6):14-18.
[2] 拉德CD,朗AC,肯德尔KN,等.复合材料液体模塑成型技术[M].北京:化学工业出版社, 2004:5. RUDD C D, LONG A C, KENDALL K N, et al. Liquid Moulding Technologies[M]. Beijing: Chemical Industry Press, 2004:5.
[3] FRANÇOIS Lebel, AMIR Ershad Fanaei, ÉDU Ruiz, et al. Prediction of optimal flow front velocity to minimize void formation in dual scale fibrous reinforcements[J]. International Journal of Material Forming,2014,7(1):93-116.
[4] CHUNG Hae Park, AURÉLIE Lebel, ABDELGHANI Saouab, et al. Modeling and simulation of voids and saturation in liquid composite molding processes[J]. Composites Part A: Applied Science and Manufacturing, 2011,42(6): 658-668.
[5] 蒋金华, 汪泽幸,陈南梁. LCM中碳纤维织物结构对横向渗透性的影响[J]. 纺织学报, 2013, 34 (1): 40-45. JIANG Jinhua, WANG Zexing, CHEN Nanliang. Effect of carbon fiber fabric structure on transverse permeability in LCM process[J]. Journal of Textile Research, 2013, 2013, 34 (1): 40-45.
[6] 陆振乾,钱坤. 利用分形理论求解织物渗透率[J]. 纺织学报, 2006, 27 (2): 17-19. LU Zhenqian, QIAN Kun. Calculate the permeability of fabric by the fractal theory[J]. Journal of Textile Research, 2006, 27 (2): 17-19.
[7] RANGANATHAN S, ADVANI S G, WISE G M, et al. A Numerical and Experimental Study of the Permeability of Fiber Preforms[J]. Advanced composites X: Proceedings of the 10th Annual ASM/ESD Advanced Composites Conference. 1994: 309-319.
[8] GOKCE A, ADVANI S. Permeability estimation with the method of cells[J]. Journal of Composite Materials, 2001, 35 (8):713-728.
[9] NGO N D, TAMMA K K. Microscale permeability predictions of porous fibrous media.pdf[J]. International Journal of Heat and Mass Transfer, 2001, 44: 3135-3145.
[10] GEBART B R.Permeability of unidirectional reinforcements for RTM[J]. Journal of Composite Materials, 1992, 26 (8):1100-1133.
[11] 李嘉禄, 吴晓青, 冯驰. RTM中纤维渗透率预测的研究进展[J]. 复合材料学报, 2006, 23 (6):1-8. LI Jialu, WU Xiaoqing, FENG Chi. Research progress on the permeability prediction of f iber in RTM[J]. Acta Materiae Compositae Sinica, 2006, 23 (6):1-8.
[12] HAPPEL J. Viscous flow relative to arrays of cylinders[J]. AIChE Journal, 1959, 5 (2):174-177.
[13] CAI Z, BERDICHEVSKY A L. An improved self-consistent method for estimating the permeability of a fiber assembly[J]. Polymer Composites, 1993, 14 (4): 314-323.
[14] GEORG B, LIN Y. Influence of fibre distribution on the transverse flow permeability in fibre bundles[J]. Composites Science and Technology, 2003, 63 (14):2069-2079.
[15] CHEN X, PAPATHANASIOU T D. On the variability of the Kozeny constant for saturated flow across unidirectional disordered fiber arrays[J]. Composites Part A: Applied Science and Manufacturing, 2006, 37 (6):836-846.
[16] 赵艳娜, 俞炜, 周持兴. 纤维截面形状与横向渗透率的关系//郑强. 中国流变学研究进展:第十届中国流变学学术会议. 杭州:浙江大学出版社, 2010: 102-105. ZHAO Yanna, YU Wei, ZHOU Chixing. The Effect of Fiber Section on the Transverse Permeability[C]//ZHANG Qiang. China Academic Journal Electronic Publishing House: 10th Acadamic Conference of Chinese Rheology. Hangzhou: Zhejiang University Press, 2010: 102-105.
[17] 赵艳娜, 俞炜,周持兴. 纤维微结构与横向渗透率的关系[J]. 复合材料学报, 2011, 8 (2): 49-53. ZHAO Yanna, YU Wei, ZHOU Chixing. Relationship between microstructure and transverse permeability[J]. Acta Materiae Compositae Sinica, 2011, 8 (2): 49-53.
Microscopic numerical simulation of transverse permeability of fiber bundles in liquid composite molding
LI Yongjing, YAN Shilin, LI Dequan, YAN Fei
(SchoolofScience,WuhanUniversityofTechnology,Wuhan,Hubei430070,China)
This paper treated the fiber bundles as porous media and researched the transverse permeability by the microscopic simulation based on Darcy law. Firstly, it builds the regular and random distribution microscopic numerical analysis models for the cross section of fiber bundles and calculates the transverse permeability of the fiber bundles under a constants pressure gradient; Secondly, it investigates the influence of the model size on the permeability values under a constant porosity, analyzes the size effect of computation model and determines the minimal size of the microscopic numerical analysis model to predict the transverse permeability; Finally, it calculates and analyzes the transverse permeability of the fiber bundles within fiber randomly distributed at different porosities, and obtains the influence rule of the porosity to the permeability values, which is compared with the results of the Gebart model and the Cell model.
liquid composite molding; transverse permeability; numerical simulation; date fitting
10.13475/j.fzxb.20140707106
2014-07-29
2015-03-13
李永静(1986—),女,博士生。主要研究方向为复合材料液体模塑成型工艺的数值模拟。晏石林,通信作者,E-mail:yanshl@whut.edu.cn。
O 351.3; TS 151
A

