轴类零件自动检测仪中工件自重力变形及补偿研究

蔡善乐 黄亚洲 王 超

(兰州理工大学数字制造技术与应用省部共建教育部重点实验室，兰州 730050)



轴类零件自动检测仪中工件自重力变形及补偿研究

蔡善乐 黄亚洲 王 超

(兰州理工大学数字制造技术与应用省部共建教育部重点实验室，兰州 730050)

提出了将工件的自重力变形误差作为一种系统误差加以补偿。在考虑剪力影响下,用有限元求解和函数逼近的方法，对该检测仪可测的等截面轴、变截面轴和梯形轴的自重力变形挠度曲线方程进行了推导。实验证明，本文求挠度曲线的方法比经典材料力学的挠度曲线公式精度高，故工件的自重力变形误差补偿成为了可能。

自重力变形误差；有限元；函数逼近；挠度曲线

0 引言

精确和快速的检测系统已成为现代机械制造中的重要组成部分。轴类零件的质量是机械产品质量的核心部分。三坐标测量机是现代制造业的重要组成部分，能够快速有效的完成通用的检测需要，但在轴类零件在线检测、大中型轴类零件精度检验等场合，常规的三坐标测量机则很难适应；关节臂式坐标测量机与传统三坐标测量机相比,有携带方便、成本低等优点，但其控制复杂，检测精度较难保证。因此，研究生产现场使用的轴类零件自动检测仪很有必要[1]。

1 系统工作原理

表1为一种用于生产现场的轴类零件自动检测仪的设计性能指标。图1为该检测仪的系统结构示意图。

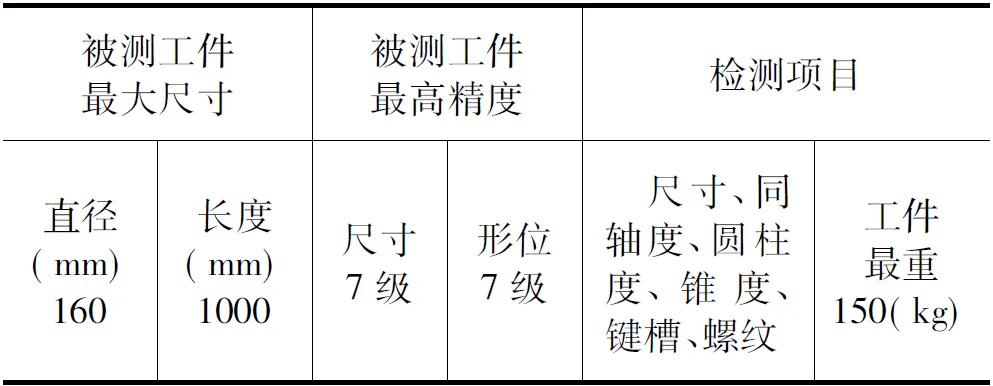
表1 检测仪设计性能指标

1.工件卡盘；2.工件；3.X向溜板；4.Y向溜板；5.探测头；6.Z向溜板图1 检测仪的系统结构示意图

该检测仪工作过程为：X、Y、Z向溜板带动探测头对工件上指定的位置进行取样，探测头接触工件轮廓的瞬间，工件停止转动，计算机系统开始采样。取得采样值后，测头离开工件表面，在工件旋转一定角度后，再次取样，直至取样完毕。

综上诉述，在工件停止转动后，计算机系统开始采样前，工件在自重力作用下将产生变形，此变形必然产生检测误差。避免该误差可采取两方面措施：一方面可以提高工件的刚度，例如在工件合适位置增加辅助支撑[2]；另一方面可以将该误差作为一种系统误差加以补偿[3-4]。第一种措施将引入新的加工、装配和调整误差，且对增加辅助支撑后的工件的刚度很难定量获得。本文将针对第二种措施进行详细研究。

2 自重力变形挠度曲线

将工件自重力变形作为系统误差来研究，须获得工件在自重力作用下的挠度曲线，为此须提取其力学模型。在图2中，图2(a)所示为工件的装夹方式；如图2(b)所示其构成了一个超静定梁；将多余约束去掉后，可简化为一个简支梁，即为工件的力学模型(自重力省略标注)，见图2(c)[5-7]。

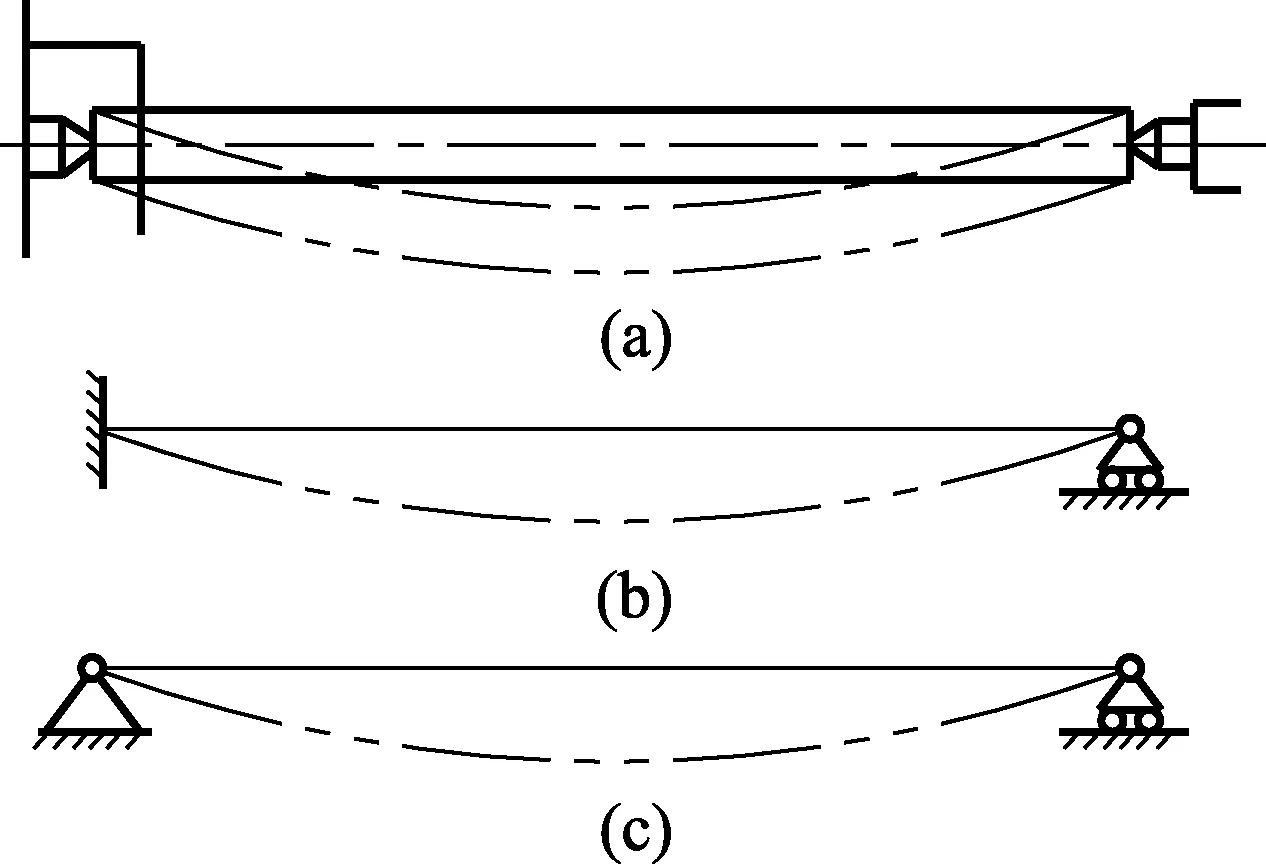
图2 被测工件力学模型

该检测仪可检测的轴类零件归为3类，如图3所示。图中，d、d1、d2分别表示直径；L、L1、L2、L3分别表示长度。

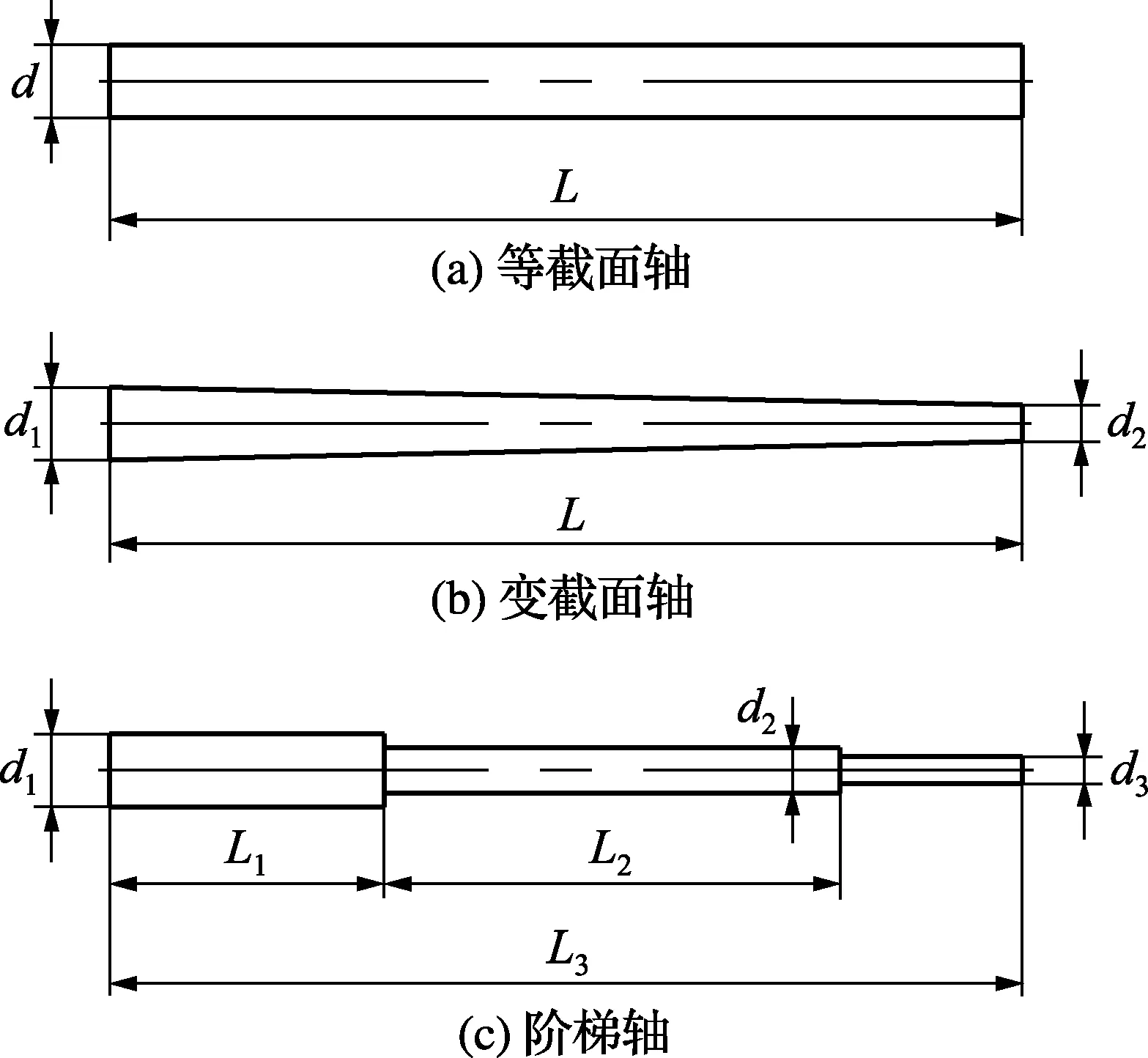
图3 该检测仪可检测的3类零件

2.1 考虑剪力影响

在经典材料力学中，等截面简支梁自重力变形的挠度曲线公式和最大挠度公式为

y=-Wx(L3-2Lx2+x3)/24EI

(1)

ymax=-5WL4/384EI

(2)

式中，W为重力；EI为截面抗弯刚度；x、L分别参照图2c和图3a。

公式(1)、(2)忽略了剪力影响，这在一般工程应用中可以满足要求，但作为有精度要求的检测仪的一种待补偿系统误差，剪力影响不能忽略。分别在是否考虑剪力影响的两种情况下，计算16种不同规格参数的等截面轴自重力变形的最大挠度，计算结果见表2。图4为长细比与相对误差关系曲线。

续表

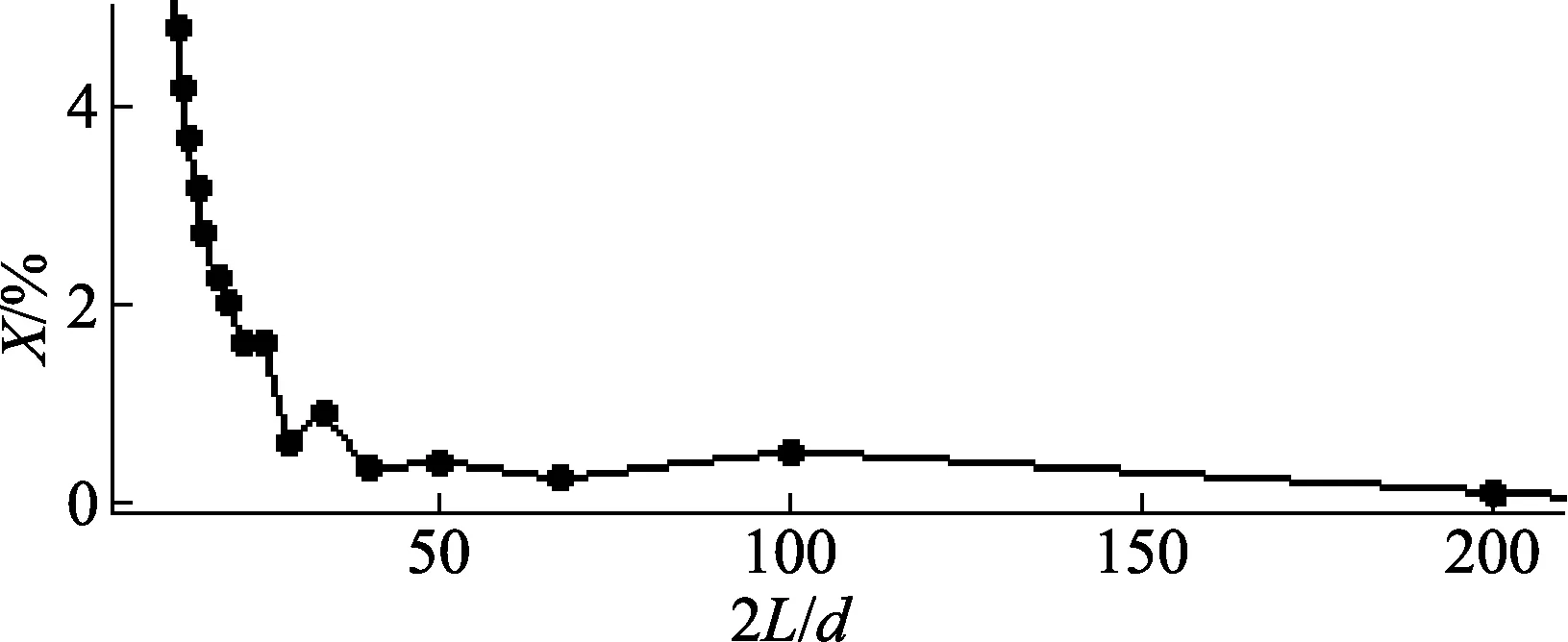
图4 长细比与相对误差关系曲线

由图4得，当长细比2L/d小于25并持续减小时，在考虑剪力影响和不考虑其影响两种情况下的最大挠度y1、y2的相对误差X%快速增大。故长细比小于25的工件的自重力变形须考虑剪力影响，须推导更精确的挠度曲线方程。

2.2 求解挠度曲线

现有的推导挠度曲线方程的方法，大多忽略剪力影响，文献[6]提出了用能量法，考虑剪力影响，推导了挠度曲线方程，但其是用来推导建筑工程中梁的挠曲线，在本文的研究领域中，该方法精度过低。本文提出了一种基于有限元方法获得工件各部分的离散挠度值，通过函数逼近的方法获得挠度曲线方程的方法。下面用该方法对表2中16号等截面轴的挠度曲线进行求解。

在ansys软件中，用beam189单元，结合图2c力学模型，对表2中16号等截面轴自重力变形进行有限元求解，可得到沿x轴方向，在长度范围内的100个离散挠度值。将这些离散挠度值输入matlab软件中的curve fitting工具箱内，用正弦曲线进行逼近，得到挠度曲线方程：

y3=a1sin(b1x+c1)

(3)

式中，a1、b1、c1分别为0.003275、0.003133、p ，x≠(0,1000)。

上式拟合结果见图5。图5(a)为拟合图，图5(b)为残差图，所有残差绝对值均小于5×10-5mm，说明拟合精度高。

图5 等截面轴16自重力变形拟合结果

2.3 实验验证

为比较公式(1)、(3)精度，在x方向上取9个挠度值进行比较，见表3和图6。

表3 挠度值比较

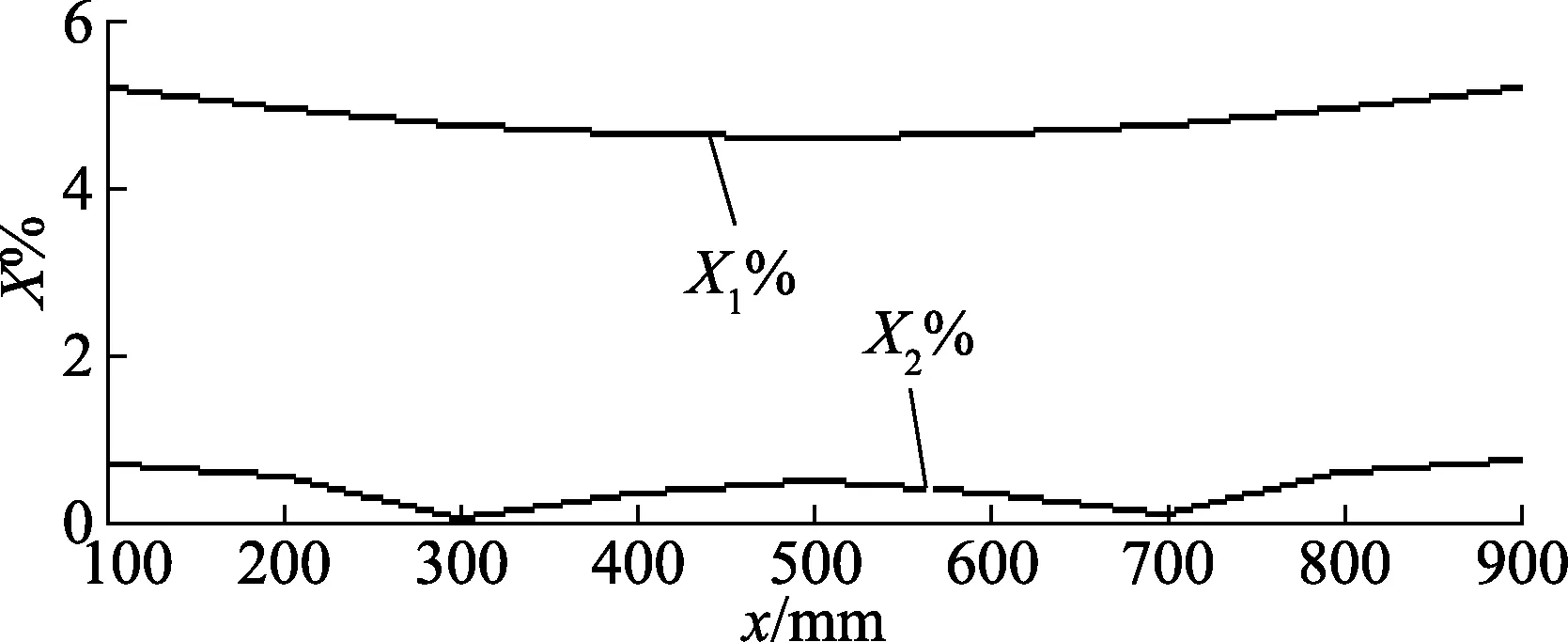
图6 相对误差比较图

由图6得出，相对误差X1%>4.5,X2%<1,故用本文方法得到的式(3)作为等截面轴自重力变形的挠度曲线方程，精度更高。根据式(3),结合具体的参数标定和补偿方法，即可将等截面轴自重力变形误差作为一种系统误差在该检测仪系统中加以补偿。

2.4 变截面轴类零件挠度曲线

用同样的方法可得到图3(b)和(c)所示的变截面轴、梯形轴的挠度曲线方程。对其分别赋值如表4。

表4 变截面轴和梯形轴参数 单位：mm

参照求等截面轴自重力变形挠度曲线方程方法得变截面轴自重力变形挠度曲线方程式(4)和拟合结果见图7。

y=a1sin(b1x+c1)+a2sin(b2x+c2)

(4)

式中，a1、b1、c1，a2、b2、c2分别为0.006807、0.003209、p ，0.0008588、0.005841、-0.1679，x≠(0,1000)。

图7 变截面轴自重力变形拟合结果

同理得，梯形轴自重力变形挠度曲线方程式(5)和拟合结果见图8。

y=a1sin(b1x+c1)+a2sin(b2x+c2)+

a3sin(b3x+c3)

(5)

式中，a1、b1、c1，a2、b2、c2，a3、b3、c3分别为0.006971、0.003225、3.09，0.0007728、0.006622、-0.7248，0.0002076、0.01209、0.3098，x≠(0,1000)。

图8 梯形轴自重力变形拟合结果

3 结论

本文利用有限元求解和函数逼近的方法，推导了等截面轴在考虑剪力影响下的自重力变形挠度曲线方程。通过实验验证得出，该方法求得的挠度曲线方程比经典材料力学的挠度曲线公式精度高，其满足在该检测仪中作工件自重力变形误差补偿用的误差数学模型的精度要求。利用该方法分别对变截面轴和梯形轴在考虑剪力影响下的自重力变形挠度曲线方程进行了推导。至此，该检测仪可检测的3类轴的自重力变形挠度曲线方程全部推导出。该项误差可用本文方法建立的数学模型进行补偿。

[1] 蔡善乐,左延红.轴类零件自动检测系统研究[D].兰州：兰州理工大学，2006,5

[2] 王先逵.机械制造工艺学[M].北京：机械工业出版社，2010

[3] Park J J，Kwon K，Cho N．Development of a coordinate measuring maehine(CMM)touch probe using a multi-axis force snsor[J]．Measurement Science and Technology，2006，17(9)：2380-2386

[4] 王学影,刘书桂.关节臂式坐标测量机系统研究[D].天津:天津大学，2008,1

[5] 聂毓琴,孟广伟.材料力学[M].北京：机械工业出版社，2009

[6] 周期源,高轩能.考虑剪切变形影响时变截面梁的挠度计算[J].南昌大学学报，2006,28(3)：295-298

[7] 刘浩，党养正，李文娟，等.基于三坐标测量的石油螺纹量规检测系统[J].计量技术，2013(1)：21-26

10.3969/j.issn.1000-0771.2015.2.09