称重法水流量装置密度的取值方法*

孟 涛 胡鹤鸣 李晓鹏 邢 超

(中国计量科学研究院，北京 100029)



称重法水流量装置密度的取值方法*

孟 涛 胡鹤鸣 李晓鹏 邢 超

(中国计量科学研究院，北京 100029)

密度是水流量计量中的重要物理量，称重法水流量装置进行空气浮力修正和密度换算需要使用实验介质密度及空气密度参与计算。当前部分水流量装置使用的密度取值方法存在密度公式来源不清、对介质成分和压力缺少修正等问题，可能会对最终测量结果造成0.03%～0.1%的误差。介绍了国际计量委员会(CIPM)推荐使用的纯水及湿空气密度计算公式，并给出了在水流量装置中的密度修正方法及不确定度分析。

水流量装置；水密度；湿空气密度；浮力修正；不确定度

0 引言

对于水密度的取值，除了采用密度计进行实测外，还可以用数学公式进行准确表征，函数化的密度公式非常便于对实验数据的自动处理，是水流量装置中较为常见的做法，但目前普遍存在的问题是：1)密度计算公式来源不清晰；2)装置用水的密度是水温、水压及介质成分的函数，很多装置缺少对后两项的修正或修正方法不正确。对于空气密度的取值，由于cr(ρa)数值较小，空气密度的测量经常被忽略，常使用常数代替(如按通常状态下设定空气密度为1.2kg/m3)，造成空气密度不确定度较大。对于不确定度0.05%(k=2)或更高水平水流量装置而言，上述取值问题都是必须要考虑的。

1 密度与流量的关系

称重法水流量装置以电子秤等衡器为主标准器，在实际工作中，经常需要将电子秤示值转换为累积体积流量，这个过程需要进行浮力修正以及密度换算，如式(1)所示：

(1)

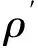
(2)

(3)

(4)

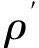
2 水密度取值

很多人认为如能对水流量装置中的介质进行实时在线密度测量，可获得最为准确的测量值，且引入的不确定度也最小，但在实际应用中是很难实施的，也是没有必要的。一方面，在线密度计价格昂贵，对其校准也较为困难，且如维护不当，容易出现偏差或漂移；另一方面，对于纯水的密度研究已相当成熟，其密度计算水平可优于0.001%，推荐2个(1个大气压下)纯水的密度计算公式。

2.1 纯水密度公式

1)Tanaka公式[3，4]

(5)

式中：ρTanaka单位是kg/m3，t为水温(℃)，各常数项取值为：a1=-3.983035，a2=301.797，a3=522528.9，a4=69.34881，a5=999.974950。该公式被认为是在0～40℃范围内最准确的公式，不确定度可以达到0.0009kg/m3，k=2。

2)IAPWS公式[3，5]

该公式来源于国际水及水蒸气物性协会(International Association for the Properties of Water and

Steam，缩写IAPWS)。

(6)

式中：ρIAPWS单位是kg/m3，tn是标准化的水温，tn=t/100，各常数项取值为：c0=999.84382，c1=1.4639386，c2=-0.015505，c3=-0.0309777，c4=1.4572099，c5=0.0648931。在常温段对比式(5)、(6)，数据如表1所示。

表1 纯水密度公式对比

对于冷水流量装置，式(5)、(6)都可以使用，其差异可以被忽略。而IAPWS公式适用的水温范围更宽，达到0～95℃，更适用于热水流量装置。

2.2 装置用水密度的修正

水流量装置一般使用自来水作为实验介质，通常其密度与纯水密度存在一定差异[6]，可以通过离线密度测量进行修正，修正值Cρ由式(7)计算得到：

Cρ=ρm-ρf

(7)

式中：ρm为密度计实测密度；ρf为相同水温下由公式计算得到的纯水密度，可以使用式(5)或式(6)。以国家水流量基准装置为例，装置介质为北京市自来水，在不同水温下，实测密度值与计算纯水密度对比结果如表2所示。

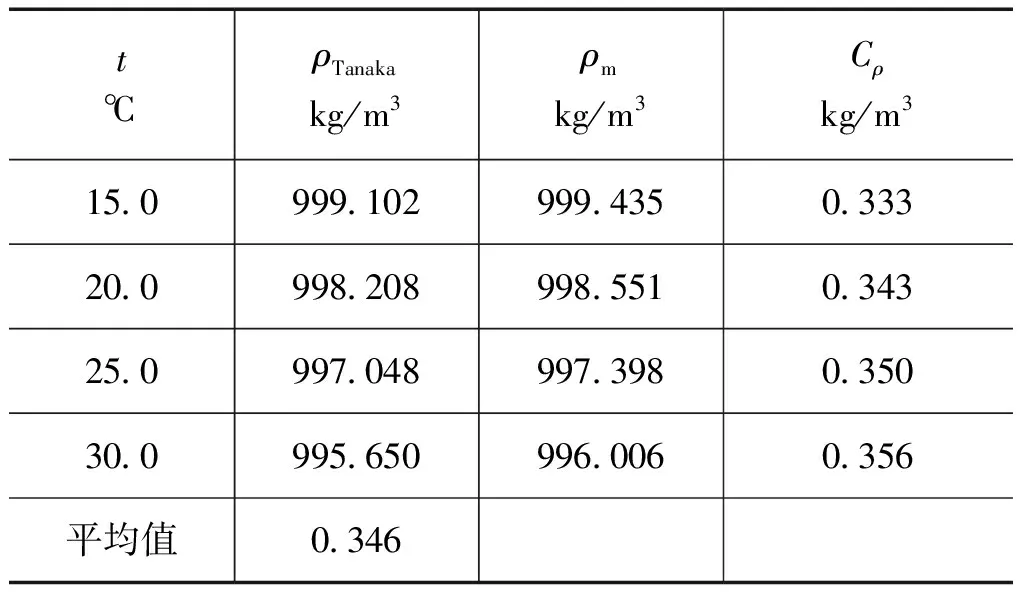
表2 密度修正值

由表2数据可知，若不对纯水密度进行修正，由此引入的误差将超过0.03%。在常温范围内，各水温点密度修正值较为接近，可近似的采用平均值作为各温度点的统一修正值。同时，由此可见，自来水密度随温度变化的特性与纯水非常相近，表2中的ρm是采用具有介质温度自动控制功能的振动管密度计，若使用传统的比重计进行密度测量，为简化实际操作，也可仅在一个常用水温点进行密度测量，使用该结果对纯水密度公式进行修正，由修正值计算方法引入的不确定度一般也是可以接受的。

而对于水温范围相对较宽的热水流量装置，特别是很多装置还对实验用水进行了软化处理，在这种情况下，建议可采用离线密度计测量并拟合“t-ρw曲线”更为稳妥。以1套热水装置实验用水为例，其密度实测结果见图1。

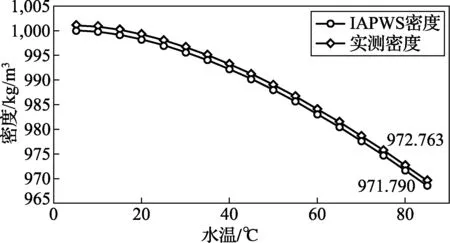
图1 热水装置介质密度测量结果对比

该实验用水经阳离子树脂交换方法软化处理后，其密度产生较大变化，比纯水密度高约0.1%，但其密度随温度变化趋势基本一致，因此，基于实验结果，采用IAPWS公式数学模型构造新的“t-ρw”公式，拟合公式中各常数项新的取值为：c0=999.84382，c1=1.4639386，c2=-0.015505，c3=-0.0309777，c4=1.4572099，c5=0.0648931。与实验数据对比，拟合公式计算结果的残差小于0.001%。

2.3 压力修正(可压缩性修正)

在称重法流量装置中，称量容器内的水压为大气压pa，被检表处为管路压力pp(表压)。因此，要计算被检表处的实际体积流量时，还要对密度进行压力修正，修正方法见式(8)：

(8)

式中：Cpl为压力修正系数，B为绝热压缩系数，单位：Pa-1，IAPWS-95也给出B的计算公式：

(9)

式中各常数项取值为：A0=5.08821×10-10，A1=1.2639418，A2=0.2660269，A3=0.3734838，A4=2.0205242。

由于通常认为水是不可压缩流体，压力修正经常被忽视。以管路表压0.2 MPa为例，计算得到Cpl=1.008，由此可见，如不进行压力修正，可能会产生约0.01%的误差，而且该误差会随着管路压力的提高而增加。

2.4 小结及不确定度分析

以普通冷水流量装置为例，综合上述修正过程，可以得到水密度计算公式：

(10)

式(10)的主要不确定度来源如表3所示。

对于不确定度水平在0.03%～0.05%(k=2)的高水平水流量装置，这里考虑若其不确定度分量的贡献若小于3×10-5，则认为该分量可以被忽略，表3中使用了一组典型数据进行分析，ρf和B公式的不确定度来源于文献[3]，t测量不确定度优于0.2℃，p测量不确定度优于2%，上述4个不确定度分量是可以被忽略的，而密度修正公式的不确定度主要取决于密度修正的获取，这主要与实测密度所使用的密度计以及修正值(或修正公式)的计算方法有关，表3中是以扩展不确定度为0.01%密度计为例进行分析。

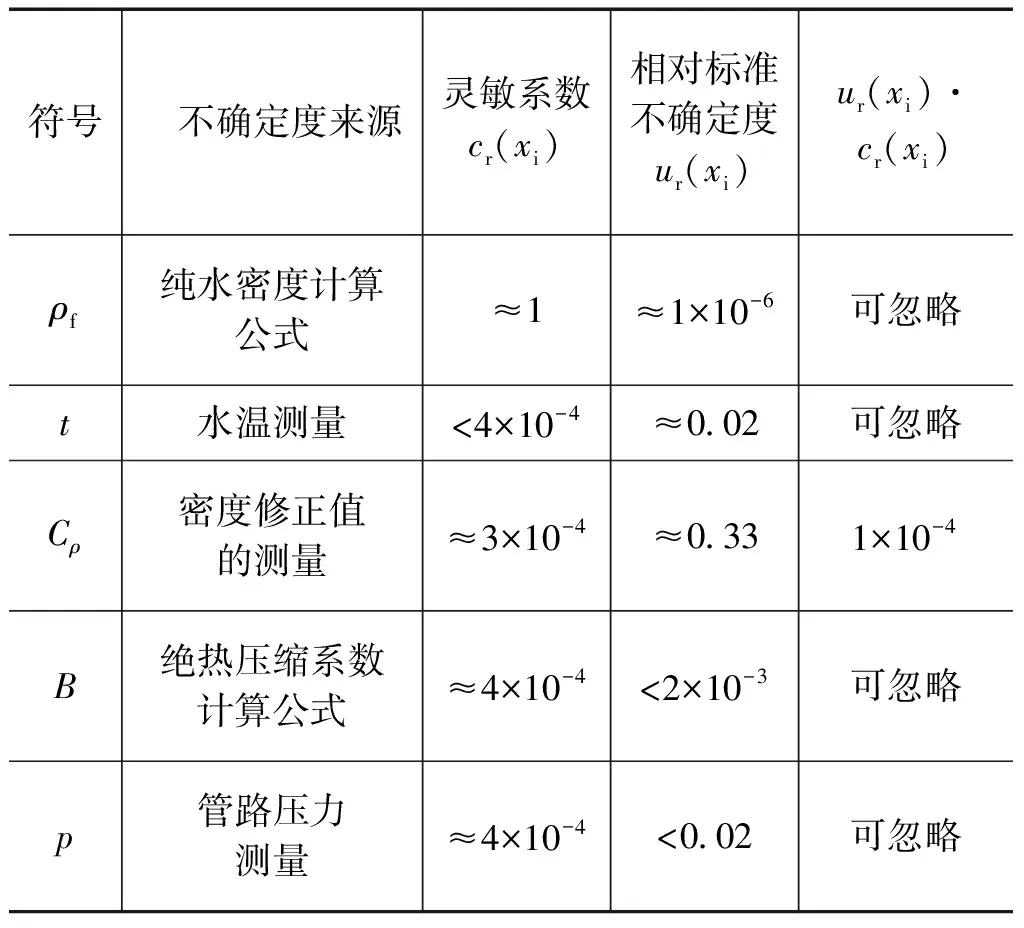
表3 密度修正公式的主要不确定度来源

3 空气密度取值

空气密度在水流量装置中主要用于称重过程中的空气浮力修正。同纯水密度一样，空气密度也可以通过公式计算间接得到，目前，最权威的湿空气密度计算公式为CIPM—2007[6]：

ρa= [3.483740+1.4446×(xCO2-0.0004)]

(11)

式中：ρa的单位是kg/m3×10-3；xCO2为二氧化碳摩尔分数，在本文中可以近似的认为xCO2=400μmol mol-1，因此，式(11)可改写为：

(12)

式中：T为气温(热力学温度)，单位：K，T=273.15+ta(ta为气温，℃)；xv为水蒸气的摩尔分数，其计算方法参考式(13)、(14)；Z为压缩因子，其计算方法参考式(15)。

xv=hf(ta,pa)·psv/pa

(13)

式中：h为大气相对湿度；f(ta,pa)为提升因子(Enhancement factor)，在一般水装置使用范围内，为简化计算可近似认为f(ta,pa)=1；psv为水蒸汽的饱和蒸汽压。

psv=1Pa×exp(AT2+BT+C+D/T)

(14)

其中：A=1.2378847×10-5K-2，B=-1.9121316×10-2K-1，C=33.93711047，D=-6.3431645×103K。

(15)

式中各常数取值为：a0=1.58123×10-6KPa-1，a1=-2.9331×10-8Pa-1，a2=1.1043×10-10K-1Pa-1，b0=5.707×10-6KPa-1，b1=-2.051×10-8Pa-1，c0=1.9898×10-4KPa-1，c1=-2.376×10-6Pa-1，d=1.83×10-11K2Pa-2，e=-0.765×10-8K2Pa-2。

使用式(12)计算得到2个不同工况空气密度，如表4所示。

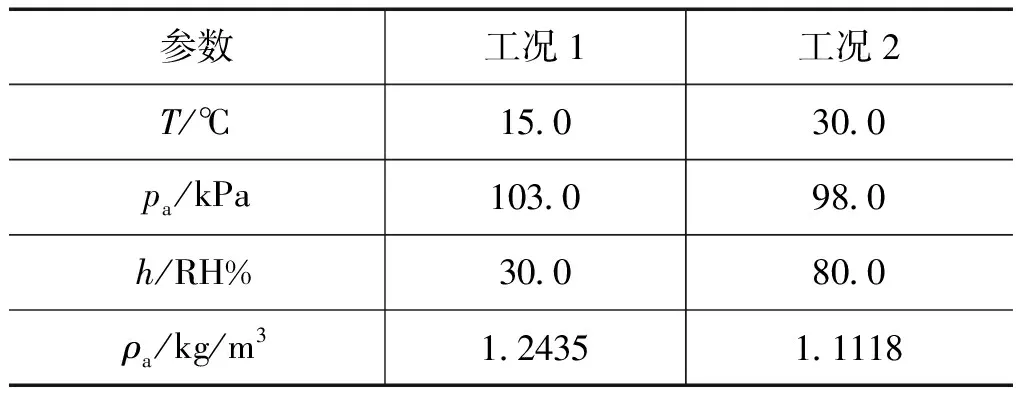
表4 不同工况空气密度对比

工况1及工况2均为常见工况，其空气密度相差11.8%。由此可见，若将ρa作为常数使用，则由此所产生的测量误差可能超过0.01%。由文献[6]可知，式(11)引入的相对不确定度为2.2×10-5，相关测量仪表即便准确度不高(如：气温测量不确定度1℃，大气压测量不确定度1%，空气相对湿度测量不确定度10%)，空气密度的不确定度仍可优于2%，该分量在水装置的不确定度分析中可以被忽略。

4 总结与讨论

随着装置不确定度水平的提升，不确定度的分析需更加细致和全面。水密度以及空气密度取值不当均可能造成最终流量测量结果误差的产生。由上述数据分析可知，综合影响可能达到0.03%，甚至超过0.1%。但实际上，应用上述方法仅需使用一些准确度指标要求并不高的测量仪器就可进行修正，修正后空气密度所引入的不确定度是可以忽略的，若能用高准确度液体密度计，如振动管式密度计准确度可达5×10-6，并可进行温度控制，直接测量t-ρw曲线，则对于一般水装置而言该项不确定度也是可以被忽略的，但仍需注意的是，在装置使用一段时间或换水后密度值可能发生变化，装置用水密度应经常进行复测。

[1] JJG 99—2006,砝码[S]

[2] 张永春, 张延福,王爱红. 砝码真空质量和折算质量计算公式实际运用中的问题和解决办法[J]. 计量技术, 2003(2)： 40-41

[3] Elsa Batista, Richard Paton. The selection of water property formulae for volume and flow calibration [J]. Metrologia, 2007, 44：453-463.

[4] M Tanaka, G Girard, R Davis, et al. Recommended table for the density of water between 0℃ and 40 °C based on recent experimental reports [J]. Metrologia 2001，38 ：301-309

[5] 蔡洁, 海宁, 林峰. 静态质量法水流量标准装置校准流量计不确定度分析的讨论 [J]. 工业计量, 2013(4)： 60-63

[6] A Picard, R S Davis, M Glaser, et al.Revised formula for the density of moist air (CIPM—2007) [J]. Metrologia, 2008, 45：149-155

国家科技支撑项目(2009BAK66B01)；质检公益行业专项(201510003)

10.3969/j.issn.1000-0771.2015.12.02