饱和土体瞬态响应有限元分析①

邱流潮， 贺向丽， 卢 海

(1.中国农业大学水利与土木工程学院，北京 100083； 2.云南省交通规划设计研究院,云南 昆明 650011)

饱和土体瞬态响应有限元分析①

邱流潮1， 贺向丽1， 卢 海2

(1.中国农业大学水利与土木工程学院，北京 100083； 2.云南省交通规划设计研究院,云南 昆明 650011)

给出基于Biot 多孔介质理论分析饱和土体在动载荷作用下瞬态响应的有限元公式，数值计算部分采用本文有限元法分别计算一维饱和土柱在两种不同类型动载荷作用下的瞬态响应，并将数值计算结果与文献中的解析解进行比较，二者结果十分吻合，从而验证本文方法的可行性。

饱和土体； 瞬态响应； 有限元法； 数值模拟

0 引言

饱和多孔土体动力响应问题的研究在岩土工程以及地震工程等领域有着非常广泛的应用价值，是土动力学中的重要研究课题。自从Biot[1-2]提出描述饱和多孔介质波动理论的基本方程以来，国内外众多学者[3-4]对饱和多孔介质动力学问题进行了研究。de Boer[5]、黄茂松等[6]和Schanz等[7]对饱和多孔介质动力学方面的研究成果做了比较详细的综述。目前饱和多孔介质动力学分析常用的方法有解析法、有限元方法及边界元法。有限元方法由于能够适应任意复杂几何形体、边界条件以及不同的材料模型而被广泛采用。本文将给出基于Biot 多孔介质理论分析饱和土体在动载荷作用下瞬态响应的有限元公式，并对一维饱和土柱在两种不同类型动载荷作用下的瞬态响应进行数值分析。

1 运动方程

基于Biot理论并忽略孔隙流体的惯性效应后，多孔介质土体运动方程可表示为[8]

(1)

孔隙流体连续方程为[9]：

(2)

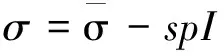
(3)

2 有限元公式

对位移变量u和孔隙水压力p引入插值近似：

(4)

(5)

式中，U和P包含u 和p离散变量(节点值)；Nu和Np为形函数。式(1)、(2)的有限元离散公式为：

(6)

式中，t+Δt表示当前时间步；Δt为时间步长。式中各矩阵和向量计算如下：

式中，B为 位移梯度矩阵；D为固体骨架的本构矩阵；α和β为Rayleigh 阻尼系数[10]。

3 数值计算

基于上述有限元公式，分析如图1所示的一维饱和土柱在两种不同类型动载荷作用下的瞬态响应，包括骨架位移和孔隙水压力。

图1 一维饱和土柱几何图Fig.1 Geometric drawing of the 1D saturated soil column

计算中为了模拟一维问题，将固体运动和流体运动限制在竖向(z向)，饱和土柱表面载荷σ(z=0，t)=f(t)，表面孔隙水压力为零。这里主要计算

f(t)为正弦载荷和阶跃载荷(step load)两种情况下的动力响应。该问题已在文献[11]中给出了解析解。为方便进行比较，本文所有计算条件均与文献[11]相同。数值计算中取土柱长10 m，宽0.5 m，用四边形单元离散。图2(a)为正弦载荷作用下的动力响应，图2(b)为阶跃载荷作用下的动力响应，从图中可以看出，本文有限元计算结果与文献[9]中的解析解十分吻合。

4 结论

本文给出了基于Biot 多孔介质理论分析饱和土体在动载荷作用下瞬态响应的有限元公式，并以此分别计算一维饱和土柱在两种不同类型动载荷作用下的瞬态响应，最后将数值计算结果与文献中的解析解进行比较。结果显示用本文方法计算饱和土体瞬态响应是可行的。需要说明的是本文方法中没有考虑孔隙水的惯性效应。

图2 动力响应Fig.2 Dynamic response

References)

[1] Biot M A.Theory of Propagation of Elastic Waves in a Fluid-saturated Porous Solid Ⅰ：Low-frequency Range[J].Journal of the Acoustical Society of America，1956，28：168-178.

[2] Biot M A.Theory of Propagation of Elastic Waves in a Fluid-saturated Porous Solid Ⅱ：Higher Frequency Range[J].Journal of the Acoustical Society of America，1956，28：179-191.

[3] 路江鑫，孙立强，曲京辉，等.地震荷载作用下饱和粉土地基液化深度试验研究[J].地震工程学报，2014，36(3)：544-548.LU Jiang-xin，SUN Li-qiang，QU Jing-hui，et al.Experimental Study on Liquefaction Depth of Saturated Silty Soil Ground under Seismic Loading[J].China Earthquake Engineering Journal，2014，36(3)：544-548.(in Chinese)

[4] 王相宝，李亮，崔智谋，等.基于流固耦合两相介质动力模型的饱和土体-地下结构体系地震反应研究[J].地震工程学报，2014，36(2)：228-232.WANG Xiang-bao，LI Liang，CUI Zhi-mou，et al.Study on the Seismic Response of Saturated Soil：Underground Structure Based on Dynamic Model of Fluid-solid Coupling Media[J].China Earthquake Engineering Jounal，2014，36(2)：228-232.(in Chiniese)

[5] De Boer R.Highlights in the Historical Development of the Porous Media Theory-toward a Consistent Macroscopic Theory[J].Applied Mechanics Reviews，1996，49：201-262.

[6] 黄茂松，李进军.饱和多孔介质土动力学理论与数值解法[J].同济大学学报：自然科学版， 2004，32(7)：851-856.HUANG Mao-song，LI Jin-jun.Dynamics of Fluid-saturated Porous Media and its Numerical Solution[J].Journal of Tongji University，2004，32(7)：851-856.(in Chinese)

[7] Schanz M.Poroelastodynamics：Linear Models，Analytical Solutions，and Numerical Methods[J].Applied Mechanics Reviews，2009，62：1-15.

[8] Hassanizadeh S M，Gray W G.High Velocity Flow in Porous Media[J].Transport in Porous Media，1987，2：521-531.

[9] Chen Zhiyun，Steeb Holger，Diebels Stefan.Analysis of Wave Propagation in the Fluid-saturated Porous Media[J].Proc Appl Math Mech，2006，6：429-430.

[10] Bathe K J.Finite Element Procedures[M].Englewood Cliffs，New Jersey：Prentice-Hall，1996.

[11] De Boer R，Ehlers W，Liu Z.One-dimensional Transient Wave Propagation in Fluid Saturated Incompressible Porous Media[J].Arch Appl Mech，1993，63：59-72.

中国地震局发布尼泊尔8.1级地震烈度图

发布时间：2015-05-01 20:35:29

2015年4月25日，尼泊尔发生8.1级强震,波及尼泊尔、中国、印度、孟加拉等国。此次地震灾区最高烈度为Ⅸ度及以上，等震线长轴总体呈NWW走向，Ⅵ度区及以上总面积约为214 700 km2，其中Ⅸ度区及以上面积约8 300 km2，长轴155 km，短轴63 km；Ⅷ度区面积约20 500 km2，长轴260 km，短轴135 km；Ⅶ度区面积约45 000 km2，长轴383 km，短轴236 km；Ⅵ度区面积约140 900 km2，长轴588 km，短轴470 km,其地震烈度图如图1。

Finite Element Analysis of the Transient Response of Saturated Soils

QIU Liu-chao1， HE Xiang-li1， LU Hai2

(1.CollegeofWaterResources&CivilEngineering，ChinaAgriculturalUniversity，Beijing100083，China；2.YunnanInstituteofTrafficPlanningandDesign，Kunming，Yunan650011，China)

An investigation of the dynamic response of saturated soil plays an important role in classical application fields such as soil mechanics，hydrology，ocean engineering and so on.Furthermore，it is essential to the development of emerging sciences and technologies，such as the mechanical characteristic of skin and soft tissue in biology.Therefore，it is important to provide appropriate theoretical analyses and numerical simulation methods.In addition，the transient response of saturated soil is also essential to the understanding of deformation and the pore water pressures generated by ground motion.This response is a key factor in the dynamic analysis of building foundations，offshore structures，and wave propagation in geological medium during blasts or earthquakes.Saturated soil is one that exhibits a solid faction and a porous space filled with a viscous fluid on a microscopic scale.Two approaches are possible for addressing the description of such a soil.The first approach is at the microscopic scale.Here，the “solid elastic” and “viscous fluid” phases each constitute distinct geometric domains.A geometric point is found at a given instant in one of these two clearly identifiable phases.The second approach considers the problem from the macroscopic level.The elementary volume is considered to be the superposition of two material particles with different kinematics occupying the same geometric points at the same instant.Thus，the saturated soil is considered as a two-phase continuum；the skeleton particle is constituted by the solid matrix and connected porous space，and the fluid particle is formed from the fluid saturating this connected porous space.There are many theories describing the characteristics of saturated soils，e.g.，Biot Theory，porous media theory，hybrid mixture theory，and so on.Most of the transient response studies for saturated soils are solved by numerical methods such as the finite element method (FEM)and finite difference method (FDM).Compared to the FDM，the most attractive feature of the FEM is its ability to handle nonlinear material and complicated geometries (and boundaries)with relative ease.In this investigation，based on Biot Theory，a mathematical model of a two-dimensional saturated elastic soil is established，and a time-domain FEM for analyzing the transient dynamic response of saturated soil under cyclic loading is presented.To verify the efficiency and accuracy of the proposed method，a one-dimensional saturated soil column subject to two different surface loadings was simulated.The first numerical example models the transient response of the saturated soil column due to sine wave loading.The second case is for the dynamic response of the soil column subject to step loading.For both numerical examples，the solid displacement history and pore pressure history are presented and compared with analytical solutions.Good agreement between the computed results and analytical solutions show the efficiency and accuracy of the proposed method.

saturated soil； transient response； finite element method； numerical simulation

图1 2015年4月25日尼泊尔8.1级地震烈度图Fig.1 Seismic intensity map of the Nepal MS8.1 earthquake on April 25, 2015

2014-08-20

国家自然科学基金面上项目(11172321)；国家自然科学基金青年基金项目(51109212)

邱流潮(1971-)，男，博士，副教授，主要从事水利工程数值仿真研究.E-mail：qiuliuchao@cau.edu.cn

TU45

A

1000-0844(2015)02-0472-04

10.3969/j.issn.1000-0844.2015.02.0472