基于多点激励位移输入模型的跨断层桥梁地震动输入方法

惠迎新 王克海

(东南大学交通学院, 南京 210096)(交通运输部公路科学研究院, 北京 100088)



基于多点激励位移输入模型的跨断层桥梁地震动输入方法

惠迎新 王克海

(东南大学交通学院, 南京 210096)(交通运输部公路科学研究院, 北京 100088)

探讨了多点激励位移输入模型对跨断层桥梁的适用性,并针对包含永久地面位移的时程曲线在基线校正过程中存在的问题提出了一种改进的基线修正方法．利用该方法对集集地震中距发震断层最近的10个强震台站地震动记录进行基线校正,校正后的永久地面位移与GPS测站同震位移运动方向一致,数值相近,由此验证了该方法的合理性,所得位移时程曲线可作为多点激励位移输入模型的地震动输入．以某跨断层桥梁为例,分别采用多点激励位移输入模型和多点激励加速度输入模型计算结构地震响应．结果表明,基于多点激励位移输入模型的地震动输入方法能够真实模拟断层错动引起的结构残余变形与内力,符合实际震害特征;而基于多点激励加速度输入模型的地震动输入方法则未考虑该残余变形与内力,故可能导致不合理的计算结果．

桥梁工程;多点激励位移输入;跨断层桥梁;基线校正

地震时跨越活动断层的桥梁结构具有较大的破坏风险,许多国家和地区出台了相关规范和条例,如禁止在活动断层之上新建桥梁或要求与活动断层之间设置一定的避让距离等．然而,对于跨越峡谷、河流等障碍物的桥梁结构,往往因各种客观条件的限制,无法完全避免跨越活动断层．在台湾集集地震、土耳其地震和汶川地震中,多座桥梁由于活动断层穿过而发生严重破坏甚至全桥垮塌[1]．

目前,针对跨断层桥梁的研究工作尚处于初始阶段．Bray等[2-3]通过对震后幸存的跨断层结构进行分析,认为设计之初对可能出现的断层错动考虑不充分,是桥梁严重损毁的重要原因．Goel等[4-5]研究了跨断层常规中小跨直线桥和曲线桥地震响应需求的简化计算方法．惠迎新等[1]总结了梁跨断层桥梁的震害特点,提出了抗震概念设计．上述研究主要从震害特征、简化计算方法等方面对该类桥梁进行了初步探讨,但未对就其地震动输入、地震响应特性、设防措施等进行研究．在跨断层桥梁中,断层相对错动会导致断层两侧支撑具有不同的地面运动特征,与常规近断层或远场地震动有显著差别,以往震害也证明了该类桥梁破坏的严重性和特殊性．为此,建立适用于跨断层桥梁的地震动输入方法,对开展跨断层桥梁的抗震研究具有重要意义,也是进一步探究其破坏机理、制定相应防御措施的关键．

本文结合跨断层桥梁地面运动特点,探讨了适用于该类桥梁的多点激励位移输入模型,基于既有近断层强震记录特征提出了一种改进基线校正方法,获得了用于动力时程分析的位移时程曲线．以某跨断层独塔斜拉桥为例,对比了不同地震动输入模型下的结构响应,讨论了适用于跨断层桥梁的地震动输入方法．

1 多点激励位移输入模型

跨断层桥梁中发震断层的相对错动会导致断层两侧桥梁支撑具有不同的甚至完全相反的地面运动特征．结构内力不仅取决于上部结构与地面运动之间的相对位移,还与支撑处地震动输入的差异有关．因此,同时考虑动位移和拟静力位移的多点激励位移输入模型可作为该类桥梁较为合理的震动输入模式．

采用集中质量矩阵,地震激励作用下桥梁结构在绝对坐标系中的分块运动平衡方程为[6]

(1)

式中,ut为绝对坐标系下上部结构非支座节点的运动向量;ug为绝对坐标系下支座节点的已知的地面运动向量;M,C,K分别为质量矩阵、阻尼矩阵和刚度矩阵,其下标aa,gg,g分别表示上部结构自由度、支座自由度和它们的耦合项;pg为支座反力向量．

(2)

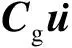
(3)

式中,-Kgug表示绝对坐标系下由于支座随地面运动而产生的作用在上部结构的力．式(3)即为求解地震多点激励下结构反应的位移输入模型．

田玉基等[7]研究了利用位移输入模型进行时程分析的数值计算方法,结果表明:适用于加速度输入模型的直接积分法同样适用于位移输入模型;若采用相同的数值积分方法和积分步长,位移输入模型可获得比加速度输入模型更高的计算精度．

2 基于近断层强震记录的基线修正

跨断层桥梁的地面运动是地震动中最为复杂的一种,以平行于断层方向的静态滑冲效应为主要特征．滑冲效应是指,受断层两侧相对错动影响,某一方向的位移时程突然升高或降低形成台阶即永久地面位移[8],在位移时程曲线中表现为末尾段与时间轴大致平行．

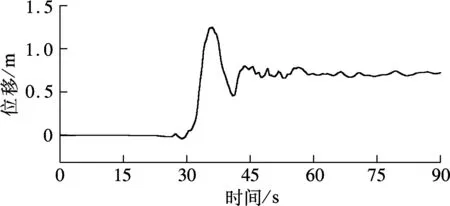
通常地震中所测地震动记录为加速度时程,而采用位移输入模型进行时程分析的有效输入信息为位移时程,需通过对加速度时程进行2次积分获得．然而,由于强震加速度记录受到环境噪音、地面倾斜等多种因素影响,直接由此数值积分得到的位移时程会出现严重的基线漂移(见图1)．若以此作为位移时程输入,将得到错误的计算结果．因此,利用既有强震记录对跨断层桥梁进行时程分析时,首先需进行基线校正,以得到具有合理永久地面位移的位移时程曲线．

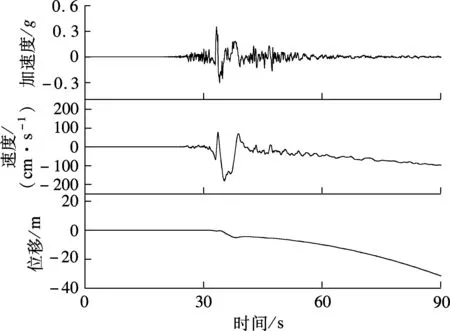
(a) 集集地震TCU052台站EW分量

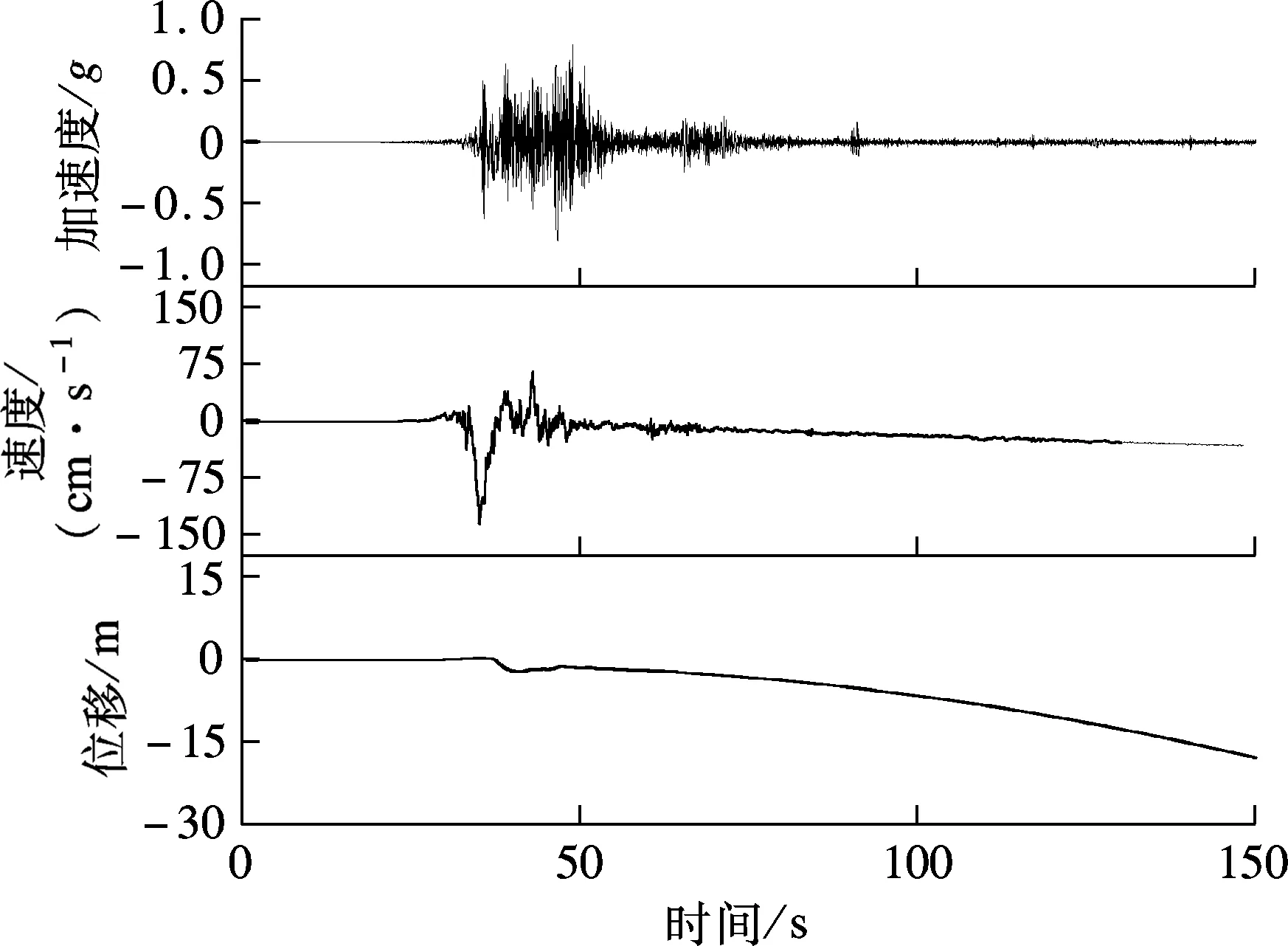
(b) 汶川地震绵竹清平51MZQ台站EW分量

在对强震记录进行基线校正时,使用最为广泛的是Iwan等[9]针对传感器磁滞效应提出的校正方法．但该方法并未考虑近断层地震动与常规远场地震动的差异,是否适用于近断层强震记录的基线修正还存在争议．理论上,在地震动到达峰值之前就会明显出现由强震仪磁滞效应导致的基线偏移;然而,在对距断层较近的地震动记录分析发现,峰值地面运动前基线偏移相对较小,基线偏移通常发生在地震动到达峰值之后．如图1(a)所示的集集地震TCU052台站EW分量,加速度峰值发生时刻约为32.92 s,而基线偏移发生时刻约为34.88 s;图1(b)所示的汶川地震波也具有相同规律．限于篇幅,本文未对集集地震和汶川地震中其他近断层地震动记录详细示例,但通过计算分析可知,它们都具有与图1中地震动时程相似的基线偏移规律,即峰值地面运动之前的基线偏移相对较小,基线偏移绝大部分发生在地震动到达峰值之后．由此可以认为,导致近断层强震记录基线严重偏离的主要原因并非强震仪有关部件的磁滞效应．相关文献也证明了这一假设,于海英等[10]对5种常用型号数字强震仪和2种型号力平衡加速度计进行了振动台对比试验,认为磁滞效应对零线漂移影响较小,导致近断层记录基线发生严重偏离的主要原因是强震仪的倾斜．

由图1中的速度时程可知,基线发生倾斜后,速度时程的斜率较稳定,呈单调线性变化,可推知加速度时程在某一时刻出现了一个整体偏移．若对整体偏移部分进行线性拟合,即可确定基线偏移的初始时刻,进而可对加速度时程进行基线校正．本文在结合既有近断层强震记录特点的基础上,提出了一种改进的基线校正方法,具体步骤如下:

① 利用直线v(t)=v+at来拟合速度时程曲线的末尾部分,其中,v和a为常系数．按最小二乘法建立差值函数,即

(4)

式中,vi为速度时程曲线上t=i时刻的速度值;Qi为t=i时刻vi与拟合曲线差值的平方和．依据极值原理,将式(4)分别对v和a求偏导,并令Qi等于零,即可求得v和a．

② 确定速度时程基线偏移的初始时刻Tw,即v(t)=0时所求拟合直线与时间轴的交点．

③ 对加速度时程进行修正,即将加速度时程中Tw至结束段对应的加速度值减去拟合直线常数a．

④ 对修正后的加速度时程进行积分,得到速度时程;在速度时程中减去震前部分平均值,再积分即可得到位移时程．

⑤ 若位移时程曲线末尾与时间轴平行,则表明基线修正完成;否则，重复步骤①～步骤④．

为验证改进基线校正方法的合理性和适用性,选取台湾集集地震中距发震断层车笼埔断层最近的10个强震观测台站(断层距均小于5 km)的加速度记录进行基线校正．断层与观测台站分布如图2左侧部分所示．理论上,GPS测站测得的地面同震位移应接近强震仪记录到的永久位移[11],因此可用GPS地面同震位移来验证改进基线修正方法的有效性．本文选取图2中地理位置相距较近的强震观测台站TCU076与GPS测站AF11(相距1.3 km)及强震观测台站TCU102与GPS测站G103(相距1.6 km)作为比较对象．GPS测站同震位移可参照文献[12]的计算结果．图2右侧部分为经基线修正并积分得到的位移时程,对应的永久地面位移见表1．

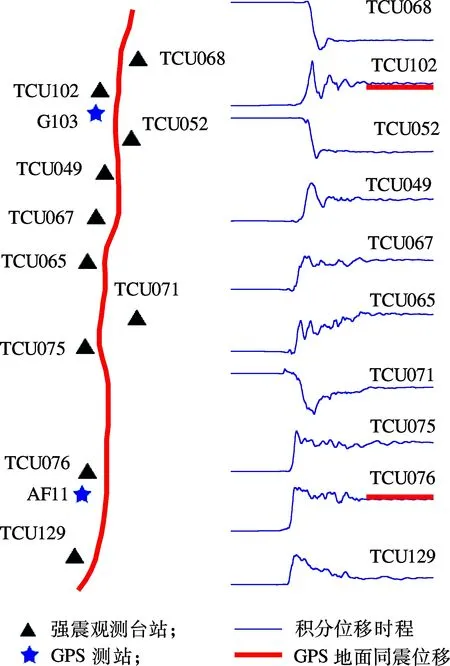
图2 经基线校正的位移时程

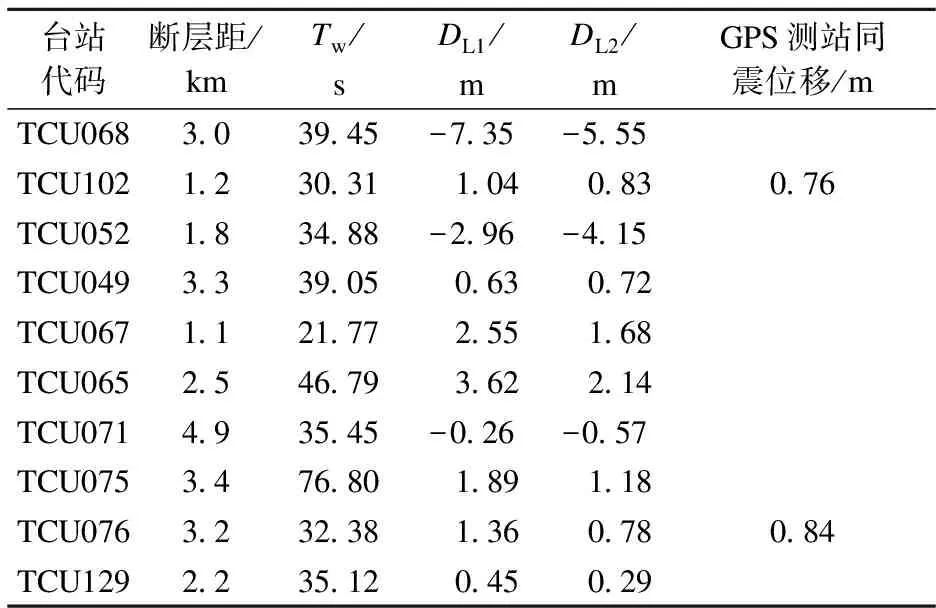
台站代码断层距/kmTw/sDL1/mDL2/mGPS测站同震位移/mTCU068303945-735-555TCU102123031104083076TCU052183488-296-415TCU049333905063072TCU067112177255168TCU065254679362214TCU071493545-026-057TCU075347680189118TCU076323238136078084TCU129223512045029

注:DL1和DL2分别为利用文献[9]方法和本文方法计算得到的永久地面位移值．

由图2和表1可知,利用本文方法所得的位移时程曲线末尾部分基本平行于时间轴,满足位移时程曲线的基线校正准则[13]．强震台站TCU076和TCU102与对应GPS测站AF11和G103的永久地面位移运动方向一致,数值相近．利用文献[9]方法所得的永久地面位移与GPS测站同震位移差别较大．

3 工程应用

以某独塔斜拉桥为例,活动断层穿过该桥的第1跨,断层走向与桥位基本垂直,桥型布置及断层走向如图3所示．图中,FP表示平行于断层方向的地震动分量．采用结构分析程序OpenSees建立有限元分析模型;主梁和桥墩采用三维线性梁柱单元模拟,斜拉索采用桁架单元模拟,桩土相互作用采用承台底加6个自由度的弹簧模拟．时程分析采用Newmark-β直接积分法,所用参数α=0.5,β=0.25．断层相对错动所产生的永久地面位移主要发生在断层错动方向,故以该方向为例进行地震动输入,并对其结构地震响应进行分析．图4为断层两侧桥墩地震动输入方向示意图．

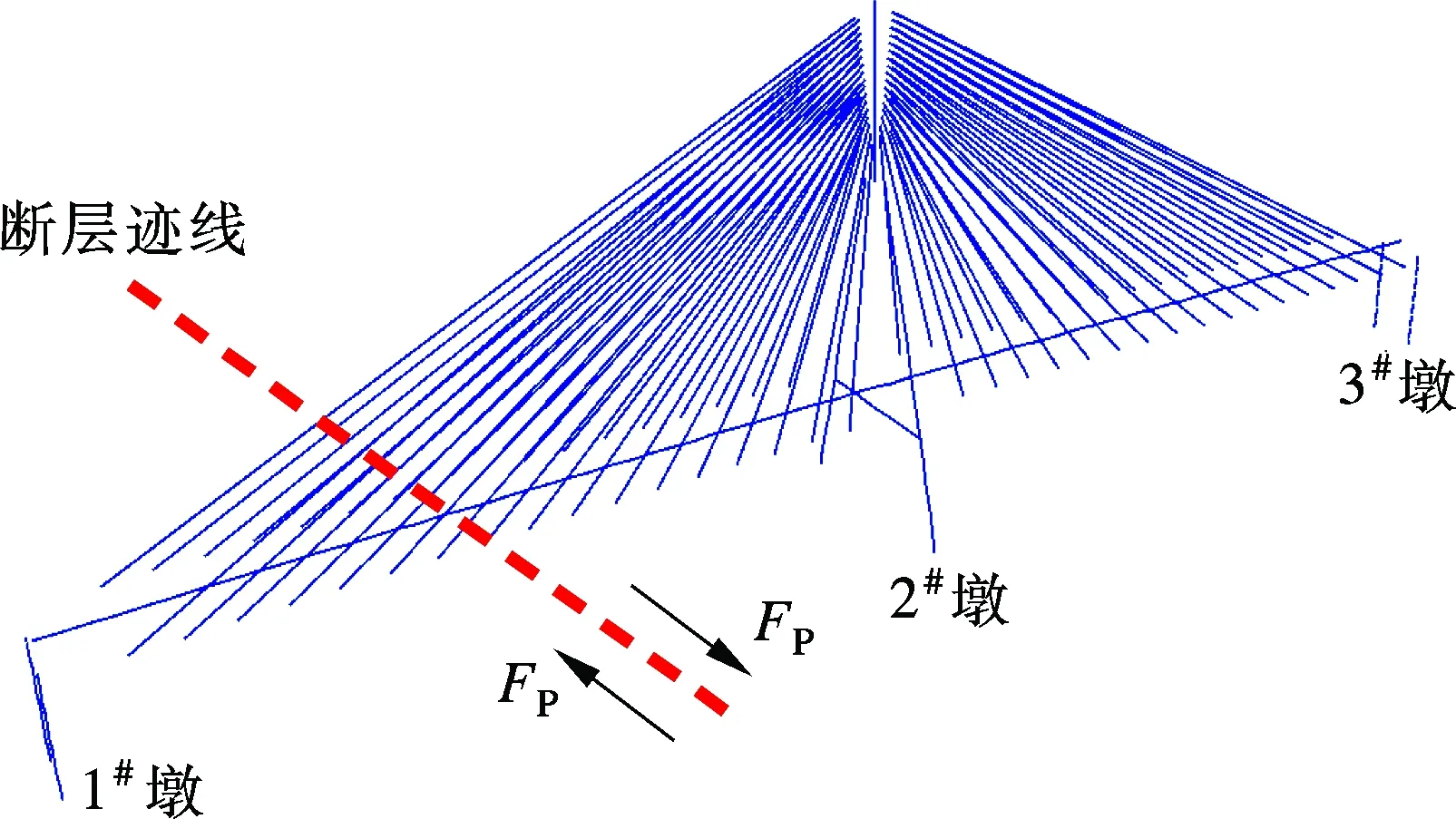
图3 桥梁总体布置和断层走向

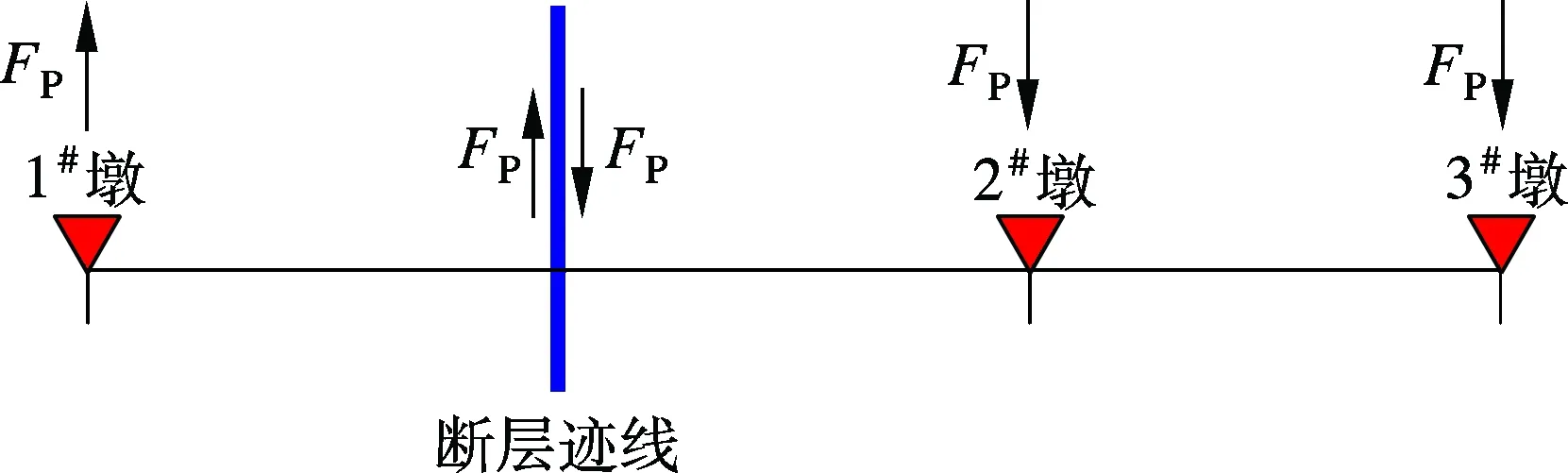
图4 墩底激励输入方向示意图

鉴于发震断层两盘地面运动衰减规律不同,以图2中距断层较近的上盘台站TCU052对应的地震动位移时程作为1#墩底的地震动输入,下盘台站TCU049对应的地震动位移时程作为2#,3#墩墩底的地震动输入(见图5(a)和图6(a))．地震动输入方式采用第1节中的多点激励位移输入模型,强震记录基线校正采用第2节中的改进基线校正方法．作为对比,还采用大质量法[14]进行了结构多点激励加速度时程分析,计算结果同样包含了结构的拟静力反应和动力反应．其墩底输入的加速度时程见图5(b)和图6(b),图5(a)和图6(a)所示的位移时程正是由此加速度时程积分得到的．

图7和图8分别为2种不同输入模型下1#和2#墩的墩身位移时程和墩底弯矩时程．由图可知,断层错动前,在2种不同输入模型作用下,1#和2#墩墩身位移响应和墩底弯矩响应的大小、形状基本一致．断层错动后,位移输入模型作用下1#和2#墩的墩身位移响应和弯矩响应向不同方向偏离原振动平衡位置,随后沿新的平衡位置往复振荡,地震动结束后存在残余位移和弯矩,这与土耳其地震、台湾集集地震跨断层桥梁的震害描述一致;而在加速度输入模型下,位移和弯矩响应值仍沿原振动平衡位置震荡,地震动结束后变形和内力值趋于0．

(a) 位移时程

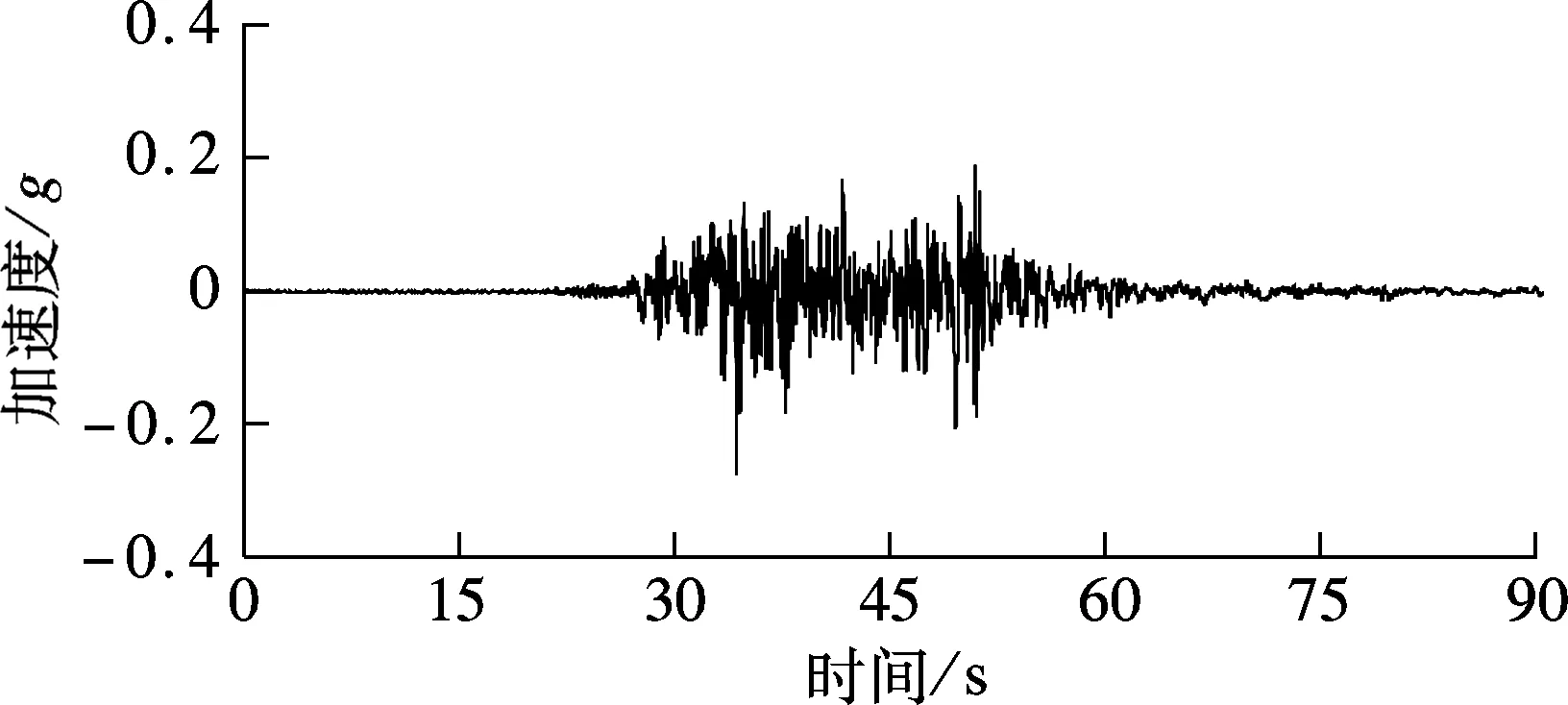
(b) 加速度时程

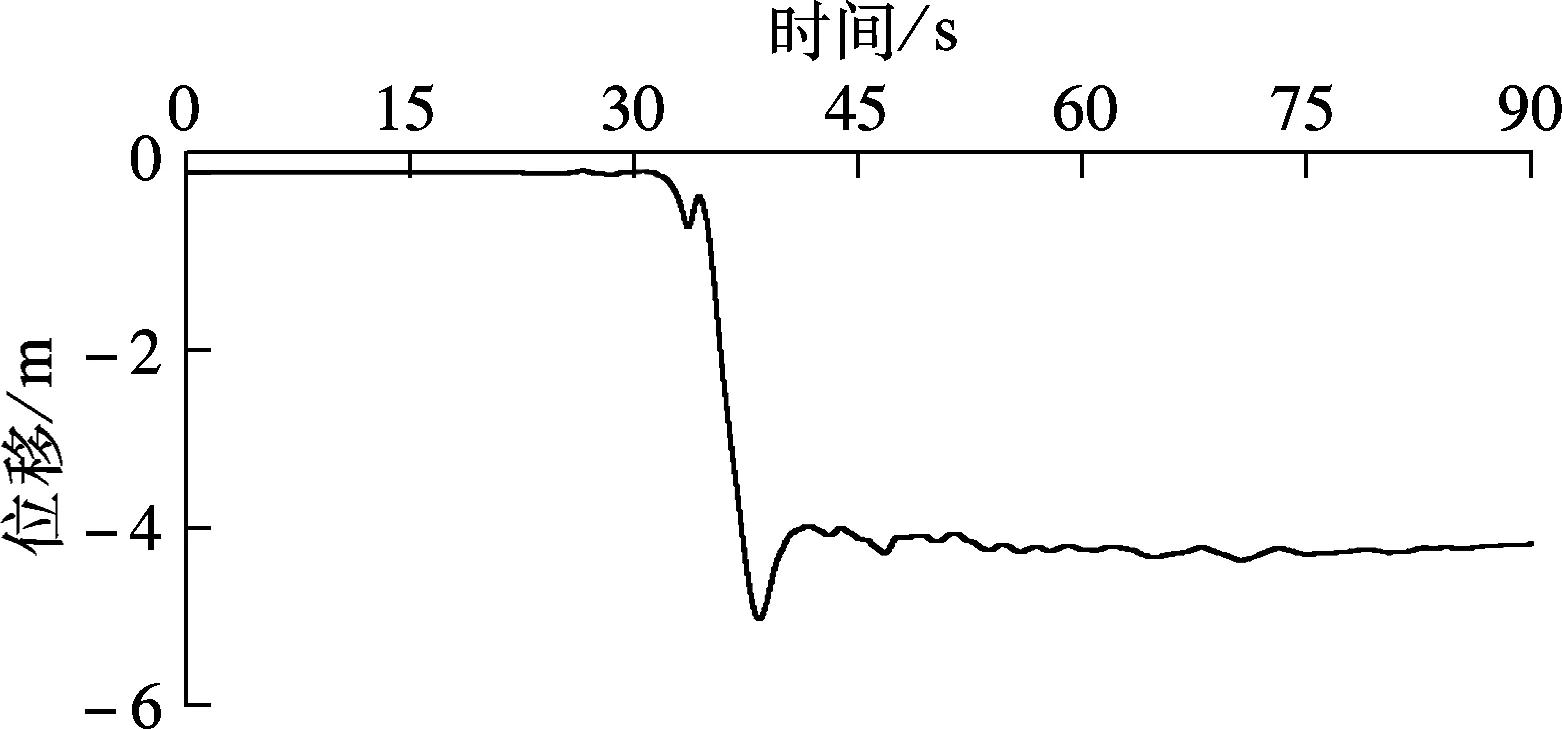
(a) 位移时程

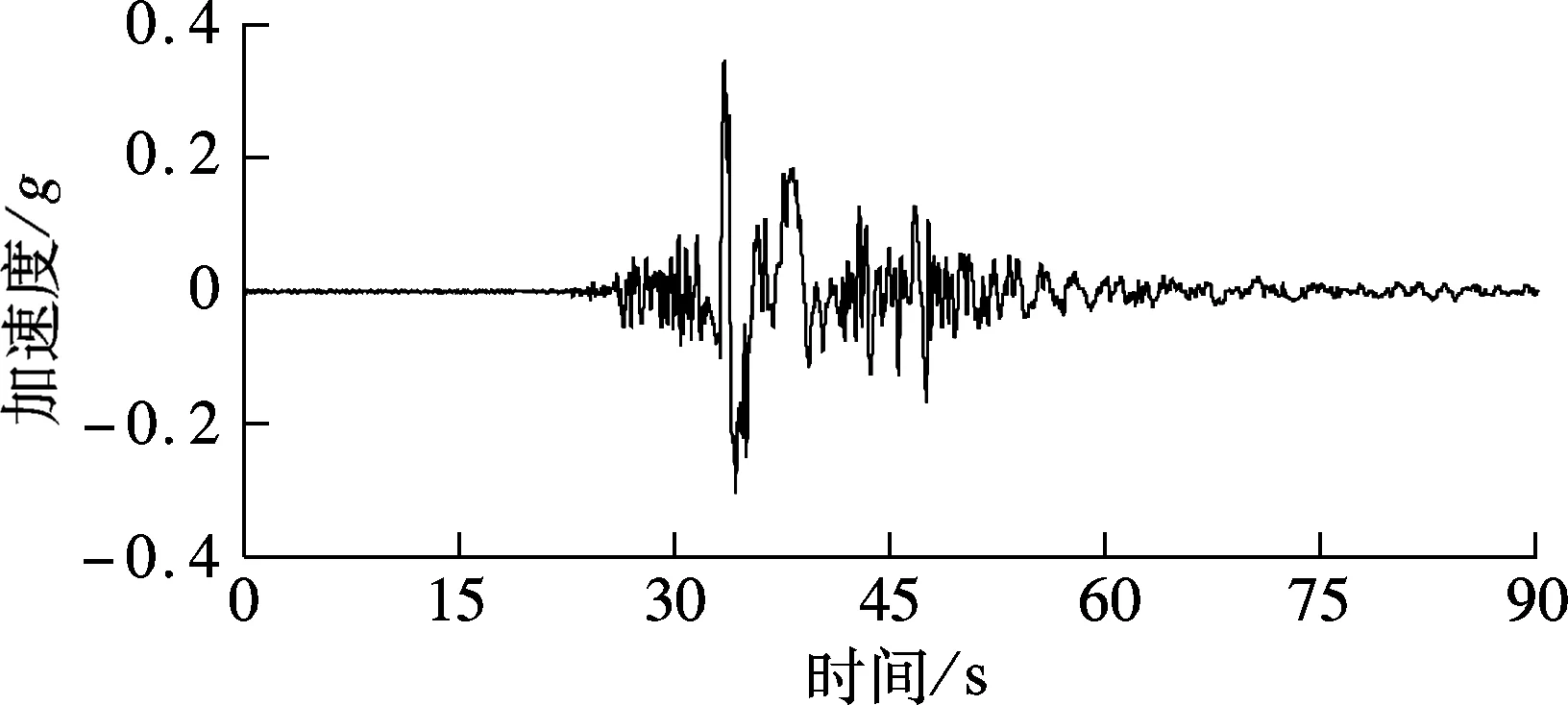
(b) 加速度时程

由此可知,基于多点激励位移输入模型的地震动输入方法考虑了断层错动地面永久变形对结构响应的影响,能够真实反映跨断层桥梁在地面运动结束后桥墩具有的残余变形和内力．而多点激励加速度输入模型对此无法考虑,可能导致不合理的计算结果．

4 结语

本文基于多点激励位移输入模型建立了跨断层桥梁地震动输入模式,采用改进方法对既有近断层加速度强震记录进行基线修正,校正后的永久地面位移与GPS测站同震位移运动方向一致,数值相近,从而验证了改进方法的合理性,所得位移时程曲线可作为多点激励位移输入模型的地震动输入．以某跨断层桥梁为例,分别采用多点激励位移输入模型和多点激励加速度输入模型,计算了结构地震响应．结果表明,基于多点激励位移输入模型的地震动输入方法能够真实模拟地表断层错动引起的结构残余变形与内力,符合实际震害特征;而基于多点激励加速度输入模型的地震动输入方法则未考虑该残余变形与内力,故可能导致不合理的计算结果．

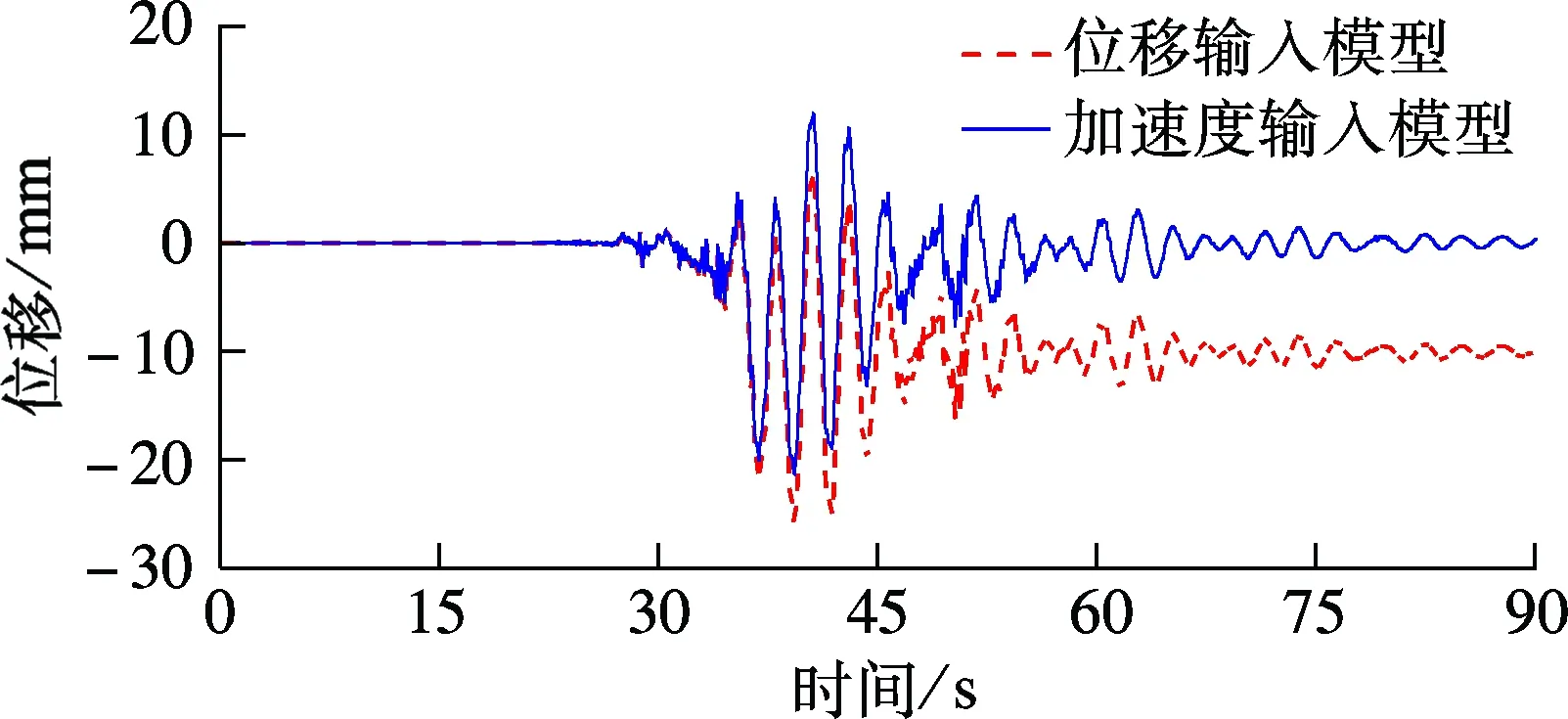
(a) 1#墩

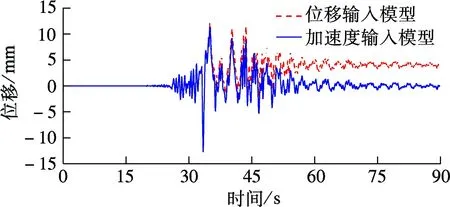
(b) 2#墩

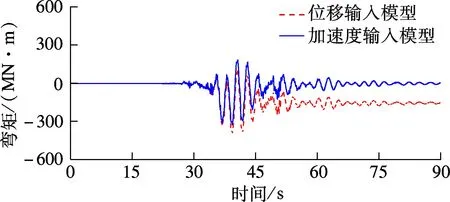
(a) 1#墩

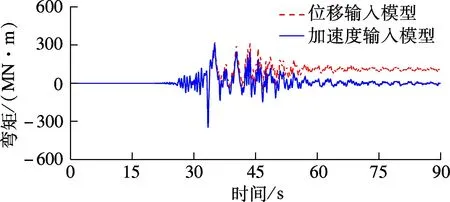
(b) 2#墩

References)

[1]惠迎新，王克海，李冲. 跨断层地表破裂带桥梁震害研究及抗震概念设计[J]. 公路交通科技, 2014, 31(10):51-57. Hui Yingxin, Wang Kehai, Li Chong. Study of seismic damage and seismic conceptual design of bridges a cross fault surface rupture zones[J].JournalofHighwayandTransportationResearchandDevelopment, 2014, 31(10): 51-57. (in Chinese)

[2]Bray J D. Designing buildings to accommodate earthquake surface fault rupture[C]//ATC&SEIConferenceonImprovingtheSeismicPerformanceofExistingBuildingsandOtherStructures. San Francisco,CA,USA, 2009:1269-1280.

[3]Park S W, Ghasemi H, Shen J, et al. Simulation of the seismic performance of the Bolu Viaduct subjected to near-fault ground motions[J].EarthquakeEngineering&StructuralDynamics, 2004, 33(13): 1249-1270.

[4]Goel R K, Chopra A K. Linear analysis of ordinary bridges crossing fault-rupture zones[J].JournalofBridgeEngineering, 2009, 14(3): 203-215.

[5]Goel R, Qu B, Tures J, et al. Validation of fault rupture-response spectrum analysis method for curved bridges crossing strike-slip fault rupture zones[J].JournalofBridgeEngineering, 2014, 19 (5):06014002-1-06014002-4.

[6]胡聿贤.地震工程学 [M]. 2版. 北京:地震出版社, 2006:180-182.

[7]田玉基,杨庆山. 地震地面运动作用下结构反应的分析模型[J]. 工程力学, 2005, 22(6): 170-174. Tian Yuji, Yang Qingshan. Analysis models and methods for structural seismic responses [J].EngineeringMechanics, 2005, 22(6): 170-174. (in Chinese)

[8]Somerville P G. Magnitude scaling of the near fault rupture directivity pulse[J].PhysicsoftheEarthandPlanetaryInteriors, 2003, 137(1/2/3/4):201-212.

[9]Iwan W D, Moser M A, Peng C Y. Some observations on strong-motion earthquake measurement using a digital accelerograph[J].BulletinoftheSeismologicalSocietyofAmerica, 1985, 75(5): 1225-1246.

[10]于海英,江汶乡，解全才，等 近场数字强震仪记录误差分析与零线校正方法[J]. 地震工程与工程振动, 2009, 29(6): 1-12. Yu Haiying, Jiang Wenxiang, Xie Quancai, et al. Baseline correction of digital strong-motion records in near-field[J].JournalofEarthquakeEngineeringandEngineeringVibration, 2009, 29(6): 1-12. (in Chinese)

[11]Wang G Q, Zhou X Y, Zhang P Z, et al. Characteristics of amplitude and duration for near fault strong ground motion from the 1999 Chi-Chi, Taiwan Earthquake[J].SoilDynamicsEarthquakeEngineering, 2002, 22(1): 73-96.

[12]Yu S B, Kuo L C, Hsu Y J, et al. Preseismic deformation and coseismic displacements associated with the 1999 Chi-Chi, Taiwan earthquake[J].BulletinoftheSeismologicalSocietyofAmerica, 2001, 91(5): 995-1012.

[13]Graizer V M. Effect of tilt on strong motion data processing[J].SoilDynamicsandEarthquakeEngineering, 2005, 25(3): 197-204.

[14]Leger P, Ide I M, Paultre P. Multiple-support seismic analysis of large structures,[J].Computers&Structures, 1990, 36(6): 1153-1158.

Earthquake motion input method for bridges crossing fault based on multi-support excitation displacement input model

Hui Yingxin Wang Kehai

(School of Transportation, Southeast University, Nanjing 210096, China) (Research Institute of Highway of Ministry of Transport, Beijing 100088, China)

The applicability of the multi-support displacement input model in bridges crossing fault (BCF) is discussed, and an improved baseline correction method is proposed to solve the problem in the process of baseline correction to ground motion time history containing the permanent ground displacements. By using this method, the ground motion records of the nearest 10 strong motion stations in the Chi-Chi earthquake are corrected. The directions of the corrected permanent ground displacements and the co-seismic of GPS stations are the same, and the values are similar, which proves the rationality of the improved method. The displacement time history can be used as the ground motion input of the multi-support displacement input model. A BCF is taken as an example, and the seismic responses of the structures are calculated by using the multi-support excitation displacement input model and the multi-support excitation acceleration input model. The results show that by using the earthquake motion input method based on the multi-support displacement input model, the residual deformation and internal force of the structures caused by fault dislocation can be truely reflected and the calculation results match with the actual characteristics of seismic damage. However, without considering the residual deformation and internal force, the earthquake motion input method based on the multi-support excitation acceleration input model may lead to unreasonable results.

bridges engineering; multi-support displacement input; bridges crossing fault; baseline correction

10.3969/j.issn.1001-0505.2015.03.025

2014-12-03. 作者简介: 惠迎新(1985—)，男，博士生；王克海(联系人)，男，博士，研究员，博士生导师，kh.wang@rioh.cn.

科技部国际科技合作计划资助项目 (2009DFA82480)、交通运输部西部交通建设科技资助项目(2009318223094)、交通运输部公路工程行业标准资助项目(JTG-C-201012).

惠迎新,王克海.基于多点激励位移输入模型的跨断层桥梁地震动输入方法[J].东南大学学报:自然科学版,2015,45(3):557-562.

10.3969/j.issn.1001-0505.2015.03.025

U442.55

A

1001-0505(2015)03-0557-06