颗粒态和溶解态磷浓度计算公式的推导与验证
李 健,金中武,杨文俊
(长江科学院河流研究所,武汉 430010)
颗粒态和溶解态磷浓度计算公式的推导与验证
李 健,金中武,杨文俊
(长江科学院河流研究所,武汉 430010)
河流水体中的含磷营养物质与较细颗粒的悬移质泥沙发生吸附作用,将对水质循环过程产生影响。基于拟合磷与泥沙颗粒吸附过程的Langmuir方程和修正Langmuir方程分别推导了计算颗粒态磷(PP)和溶解态磷(DP)的计算公式。并采用香溪河泥沙样品的磷吸附实验数据和野外观测数据验证了推导公式,计算结果与实测值符合良好。研究结果表明:当悬移质泥沙浓度较低时,可采用线性吸附方程近似计算颗粒态和溶解态磷浓度,但当悬移质泥沙浓度较高时,需要采用本研究推导的计算公式,特别是解吸和吸附现象并存时,需要使用基于修正的Langmuir模型推导的计算式。研究成果可用于水质或水生态模型建模。
悬移质泥沙;颗粒态磷;溶解态磷;浓度;吸附-解吸;香溪河
2015,32(01):33-38
1 研究背景
在很多湖泊、水库和海洋等水域中,磷元素都是浮游藻类生长的限制性营养物质,过量的磷会导致水华、赤潮或相关水质问题。磷在自然水体中以2种形式存在:①溶解态磷,包括溶解态的有机磷和无机磷;②颗粒态磷,包括存在于浮游藻类细胞中的磷或吸附于颗粒物质(如悬移质泥沙颗粒)上的磷[1]。因此吸附有磷等营养物质的泥沙是面源污染的主要来源,而水土流失、农耕等将增大流域的泥沙输出,这部分泥沙进入河道中也将增大水体的营养物质含量,引发诸多水质问题,水体、泥沙与营养物质之间的物质交换(吸附-释放过程)是水体富营养化过程的重要组成部分。
影响泥沙颗粒吸附重金属及污染物的因素有很多,诸如泥沙浓度、颗粒粒径及比表面积、絮凝、水流紊动等[2-3],最终的吸附效果可采用Langmuir和Freundlich等模型来描述[4],也可采用动力学模型来描述[5-6],而需要区分计算吸附态和溶解态营养盐(包括氮磷物质等)浓度还需要做进一步的公式推导。为此有一些简单的推导计算式已应用于水质模型中,如WASP模型采用吸附态与溶解态磷浓度呈线性关系的假定,但这仅适用于悬沙浓度很低的情况,CCHE3D_WQ模型的模拟结果表明溶解态磷浓度不仅取决于水体中初始磷浓度,还取决于悬移质含沙浓度[1,7],但该模型没有考虑磷浓度变化后泥沙释放磷的过程(解吸过程)。
另外,有研究表明三峡水库库区的悬移质泥沙对磷元素产生明显吸附,导致部分支流(如香溪)的底泥含有大量磷营养物质[8],对三峡库区的水质构成极大的威胁。除此以外,长江上游的河道水质监测数据也表明吸附有磷营养物质的泥沙沉积于一些水库(如溪洛渡水库)将使三峡水库的溶解态磷浓度增大6.8%[9]。综上所述,从水质模拟和工程实践的角度,均有必要对泥沙与营养物质经过吸附-解吸过程达到平衡态后的溶解态和颗粒态浓度计算进行研究。
本研究在Langmuir模型和修正的Langmuir模型的基础上,根据质量守恒原则,推导出计算颗粒态磷和溶解态磷浓度的计算公式,并对比2种推导公式的计算精度与适用性,最后采用香溪河泥沙样品的磷吸附实验数据和野外观测数据对推导的计算公式进行验证。研究结果可应用于为更科学的水生态数学模型建模。
2 泥沙-磷吸附方程概述及评价
目前用于拟合泥沙颗粒与磷之间的吸附-解吸过程的公式有很多种形式[4,6],罗列如下:


式中:Q为每单位重量的泥沙上吸附磷的量(mg/g);Qm为最大吸附量(mg/g);K(式中的Kc,KFr,Kl和Kml)为吸附或释放速率系数(L/mg),不同方程的K值不同;Cd为达到吸附平衡状态时溶解态磷浓度(mg/L);Cadd为初始磷溶液浓度变化值(mg/L);s为悬移质泥沙浓度(mg/L);NAP为初始吸附态磷含量(mg/g);A,B,n均为常数。
以上的吸附方程在各研究领域均被广泛应用,如WASP模型中即采用简单的线性吸附方程(1)。很多研究者采用实验或现场观测数据检验了上述各种吸附方程的适用性,证明Langmuir方程和修正的Langmuir方程的拟合效果最好。但是当存在解吸作用时,Langmuir公式得不到较好的拟合效果,因为NAP部分可释放入水体。Zhou等[10]对Langmuir方程进行了修正,修正的Langmuir方程可以很好地拟合同时存在吸附和解吸作用的过程。并且,Langmuir方程和修正的Langmuir方程具有一定的物理意义,如其中的Qm和K与泥沙的矿物成分(Fe和Al含量)相关,可以理解为铁和铝在吸附和释放磷元素中的主导作用。另外,水体的pH值、氧化还原电位势能对泥沙-磷的吸附过程产生影响,Langmuir方程可以有效地反映出泥沙-磷吸附力学机理[10]。其他几种计算式目前的应用没有Langmuir方程应用广泛。因此本研究的公式推导以Langmuir方程和修正的Langmuir方程为基础。
3 磷与悬移质泥沙吸附-解吸公式推导
吸附-解吸过程发生于水体中的溶解磷酸盐和悬移质泥沙之间。吸附过程即溶解磷酸盐(主要为正磷酸盐)与悬移质泥沙颗粒发生相互作用。解吸过程是吸附过程的逆过程,是由泥沙颗粒释放出磷酸盐成分。
因为由悬移质泥沙对磷酸盐的吸附-解吸过程的反应速率比生物反应过程要快得多,可以假设存在这样的吸附平衡状态[7]:当有磷溶液输入到河流中时,溶解态磷和颗粒态磷立即向平衡状态进行分配,即总磷在“平衡态”的溶解态磷浓度和固相的颗粒态磷浓度之间的再次分配。
3.1 不考虑NAP作用的公式推导
因为是在很短的时间内达到吸附-解吸平衡状态,因此可以假设在吸附之前和之后,磷-水-悬移质泥沙组成的溶液体积V不变。根据质量守恒法则,溶液中的磷的总量为常数值,即

式中:Cp0,Cd0分别为颗粒态磷和溶解态磷的初始浓度(mg/L);s为悬移质泥沙浓度(mg/L);V为磷-水-泥沙混合体的体积(L);Cp,Cd分别为达到吸附平衡态后的颗粒态和溶解态磷的浓度(mg/L),即:

其中C0为混合体溶液中磷的总浓度(mg/L),可表示为C0=Cp0+Cd0。
将式(8)和式(9)代入式(4),化简后可得到方程

利用根与系数关系,可求得


结合式(9)和式(12),可得到溶解态磷浓度的计算公式为

Cp和Cd由溶质的初始浓度C0、吸附常数K和吸附能力Qm,以及悬移质泥沙浓度s决定。可以看出Cp/Cd不是一个常数值。
3.2 考虑NAP作用的公式推导
首先,不做任何假设,直接求解修正的Langmuir方程中的Cd,可得到一个关于Cd的二次方程式,即


同样,根据根与系数关系,求解Cd可得
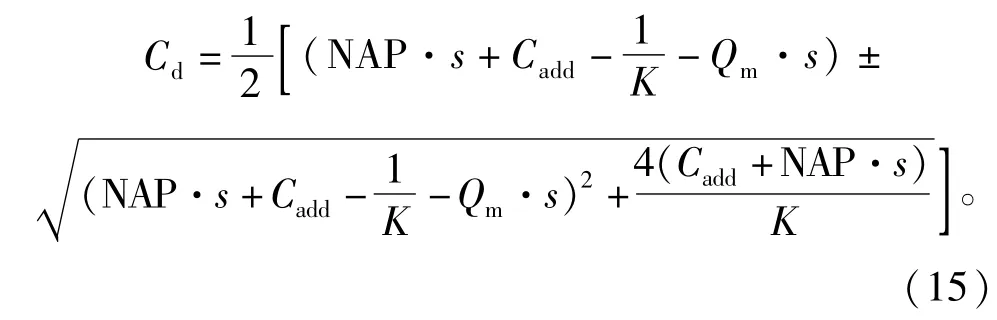
如果对式(15)取减号,因为有
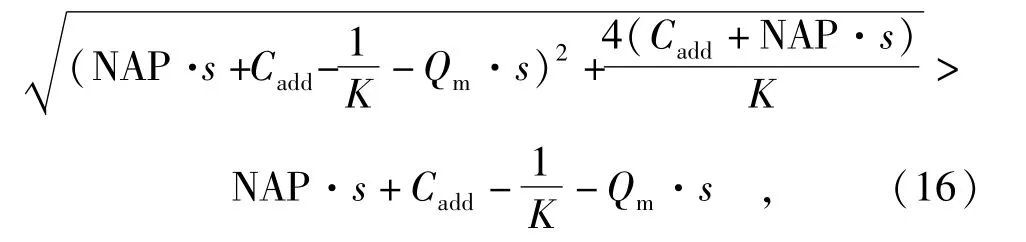
则Cd﹤0,没有物理意义,因此对式(15)只能取加号,可得考虑NAP作用下达到吸附平衡态后溶解态磷浓度的计算公式为

(1)假设Cadd为河流短时间内磷初始浓度的变化值,即。当Cadd远小于时,即不考虑NAP部分的作用,联合式(9),可得到颗粒态磷Cp的计算公式为
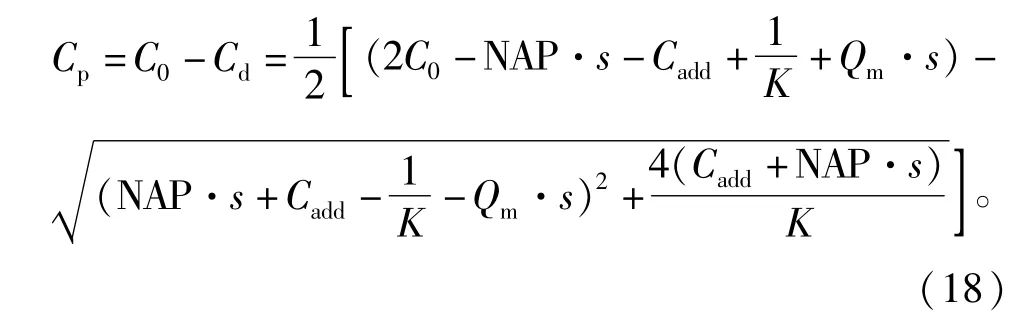
(2)当Cadd=0,即初始含磷溶液浓度没有变化或没有添加新的磷溶液,并且当时(即原始溶液中所有的磷均为可交换性磷),式(17)将退化为式(13),即Langumir公式推导出的溶解态磷计算式是由修正的Langumir公式推导出的溶解态磷计算式的一个特例。
4 吸附-解吸公式的验证
香溪河自北向南流经湖北省的兴山县和秭归县,是三峡库区内长江的一级支流,距离三峡大坝很近(仅36 km),由于上游存在严重的面源污染和磷矿开采等造成的点源污染,造成近年内香溪库湾水质恶化,发生了很多次水华事件。如图1,三峡大学香溪河野外生态试验站在香溪河沿程布置了11个测点,监测香溪河水华期间的水质演变过程。针对香溪河开展的水华监测和分析研究成果较多,资料丰富,因此本研究采用香溪河泥沙与总磷的室内实验和野外现场监测数据,分别对以上推导的公式进行验证。本研究的公式验证,以水体中的总磷(TP)作为初始溶解质浓度,将吸附平衡后水体中的正磷酸盐(PO4)作为溶解态磷浓度。
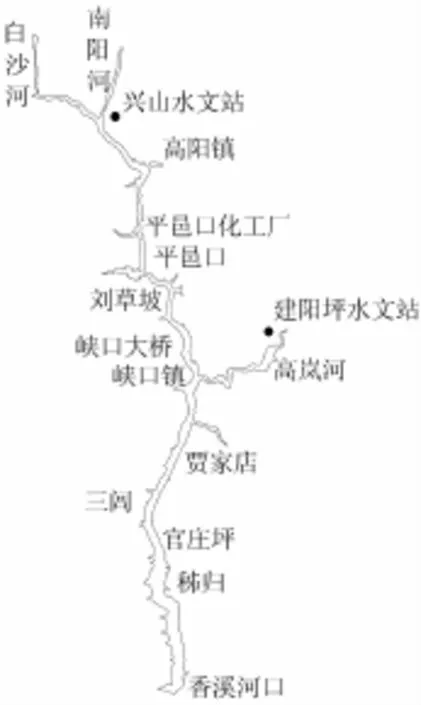
图1 香溪河平面示意图Fig.1 Schematicmap of Xiangxi River
4.1 室内实验数据验证公式
首先,采用香溪河泥沙与磷吸附的室内实验数据来验证公式[11-14]。实验温度20℃,实验中磷初始浓度分别为0,0.5,1,2,3,4,5,6 mg/L,在50 ml的溶液中加入0.5 g干燥泥沙并震荡至均匀,放置48 h后,吸附过程达到平衡。本研究采用这些实验数据拟合香溪河磷与悬移质泥沙吸附过程,并率定相关计算公式中的系数。如图2,拟合结果表明:溶液中的磷酸盐浓度和吸附量可以用Langmuir方程和修正的Langmuir方程表示。最大吸附量Qmax、吸附速率系数K和NAP由实验数据拟合获得。各公式的拟合系数见表1。
如图2所示,在初始磷浓度较高的情况下(C0>1 mg/L),Langmuir方程对磷吸附平衡过程的拟合效果与修正的Langmuir方程相差不大,但当初始磷浓度较低时(C0﹤1 mg/L),Langmuir方程的误差逐渐增大,并且不能拟合出低浓度磷溶液时由泥沙颗粒释放磷的过程,而修正的Langmuir方程可以较好地拟合整个吸附-解吸过程(图2和图3中y轴的负值浓度表示由泥沙颗粒释放一定浓度的磷),见表1,修正的Langmuir方程的拟合系数R2达0.967。

图2 不同初始磷浓度吸附等温曲线拟合Fig.2 Adsorption isotherm regression at different initial TP concentration

表1 拟合公式参数Table 1 Coefficients of the regression formula
如图3所示,分别采用由Langmuir方程和修正后的Langmuir方程推导的颗粒态和溶解态磷计算公式,计算值与实验观测值符合较好。由图3(a)可见由修正的Langmuir方程推导出的计算公式能更好地计算出较低初始磷浓度时的颗粒态磷浓度。由图3(b)可见Langmuir方程推导的溶解态磷浓度计算式的计算值比实测值偏大,拟合系数为0.832,而由修正的Langmuir方程推导出的计算公式对吸附-解吸过程的拟合系数可达0.953。可见,式(17)能更精确地计算溶解态磷浓度。

图3 不同初始磷浓度吸附平衡后的磷浓度Fig.3 Concentrations of phosphorus versus initial concentrations at equilibrium
4.2 采用香溪河现场实测数据验证公式
使用2007年9月香溪河发生水华期间监测到的水质数据,对推导的公式进行验证[12-13]。验证过程中,有关参数采用Wang et al(2009)[11]室内实验数据拟合值。本研究选择香溪河口、峡口镇和高阳镇3个代表性的测点监测数据。如图4,香溪河口处的悬移质泥沙浓度受长江干流较高泥沙浓度水体的倒灌影响,浓度较香溪河上游要大且波动也很明显;高阳镇的悬移质泥沙浓度较河口处低且波动较小,但受上游来沙影响,浓度较峡口镇大;峡口镇处于低流速区,大量悬移质泥沙沉积于河床,因此悬移质泥沙浓度低且波动很小。

图4 香溪河实测悬移质泥沙浓度(2007年)Fig.4 M easured concentration of suspended sediment in Xiangxi River(2007)
如图5,将总磷浓度作为初始磷浓度,实测的可溶性磷酸盐(PO4)浓度作为溶解态磷浓度(Cd),研究果表明:在考虑了香溪河实测悬移质泥沙浓度的情况下(图4),由修正的Langmuir方程推导的公式计算得到的溶解态磷浓度与实测浓度过程符合良好,表明推导的公式具有良好的计算精度,可以将溶解态和颗粒态的2部分量精确地区分开来,为水生生态模型的精确模拟奠定基础。

图5 溶解态磷计算值与实测值比较Fig.5 Calculated and observed concentrations of dissolved phosphorus
如图6所示,香溪河口的泥沙浓度高,因此Cp/Cd值的波动较大,范围在0.5~1.5之间。高阳镇的泥沙浓度也较大但较河口的要小,因此Cp/Cd的波动范围在0.8~1.6之间,峡口镇泥沙浓度小且基本无波动,因此Cp/Cd≈1.1。可见,当悬移质泥沙浓度高时不能采用线性计算公式,需要采用由修正的Langmuir模型推导的颗粒态与溶解态磷浓度计算公式。
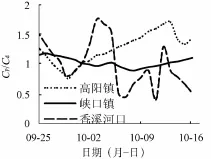
图6 颗粒态与溶解态磷浓度比值变化过程Fig.6 Variation of the ratio of PP to DP
另外,由以上的公式推导过程可以看出:泥沙与磷物质间的吸附-解吸过程受到众多因素的影响,本研究得到的计算公式具有一定的局限性,没有研究不同粒径泥沙的吸附过程,根据香溪河的水沙条件状况,建议公式使用范围为泥沙级配分布均匀且较细(D50﹤0.1 mm),有一定含沙浓度(C>0.1 kg/m3)的水体中的营养物质转换计算。
5 结 论
本研究分别基于拟合磷与泥沙颗粒吸附-解吸过程的Langmuir方程和修正的Langmuir方程,推导了用于计算附着于泥沙颗粒的颗粒态磷浓度和溶解于水体中的溶解态磷浓度的计算公式,该计算公式与泥沙颗粒吸附磷的最大能力、吸附速率系数和悬移质泥沙浓度有关,当悬移质泥沙浓度较高时,基于修正的Langmuir方程推导的颗粒态磷与溶解态磷浓度计算公式(式(17)和式(18))可更精确地计算溶解态与颗粒态磷浓度,并且可计算同时存在磷吸附-解吸过程下的溶解态与颗粒态磷浓度。
推导的颗粒态磷与溶解态磷浓度计算公式可以很好地计算出香溪河泥沙浓度较高情况下的颗粒态和溶解态磷的浓度,进一步证明线性方程更适用于泥沙浓度很低的条件。在泥沙浓度较高以及存在吸附-解吸过程时,需要采用基于修正的Langmuir方程推导的计算公式(式(17)和式(18))。最后给出了本公式的使用限制条件。本研究推导的公式可以应用于生态动力学模型中泥沙与营养物质的耦合计算。
[1]CHAO X B,JIA Y F,CHARLESM C,et al.Development and Application ofa Phosphorus Model for a Shallow Oxbow Lake[J].Journal of Environmental Engineering(ASCE),2006,132(11):1498-1507.
[2]惠二青,江春波,刘德富,等.动水条件下悬浮态泥沙颗粒吸附TP规律探讨[J].泥沙研究,2009,(2):34-38.(HUIEr-qing,JIANG Chun-bo,LIU De-fu,et al.Phosphorus Adsorption Rule of the Suspended Silt in the TurbulentWater Body[J].Journal of Sediment Research,2009,(2):34-38.(in Chinese))
[3]肖 洋,陆 奇,成浩科,等.泥沙表面特性及其对磷吸附的影响[J].泥沙研究,2011,(6):64-68.(XIAO Yang,LU Qi,CHENG Hao-ke,et al.Surface Properties of Sediments and Its Effect on Phosphorus Adsorption[J].Journal of Sediment Research,2011,(6):64-68.(in Chinese))
[4]禹雪中,钟德钰,李锦秀,等.水环境中泥沙作用研究进展及分析[J].泥沙研究,2004,(6):75-80.(YU Xue-zhong,ZHONG De-yu,LI Jin-xiu,et al.Review of Study on Sediment in Water Environment[J].Journal of Sediment Research,2004,(6):75-80.
[5]HUANG SL,WAN ZH,SMITH P.NumericalModeling of Heavy Metal Pollutant Transport-transformation in Fluvial Rivers:A Review[J].International Journal of Sediment Research,2007,22(1):16-26.
[6]黄岁梁,万兆惠,王兰香.重金属污染物动态吸附实验及数学模拟[J].水动力学研究与进展A辑,1994,9(4):437-447.(HUANG Sui-liang,WAN Zhao-hui,WANG Lan-xiang.Study of Dynamic Experiment and Mathematical Modeling on Sediment Adsorption of Heavy Metal Pollutant[J].Journal of Hydrodynamics,Series A,1994,9(4):437-447.(in Chinese))
[7]CHAO X B,JIA Y F,DOUGLASSHIELDSJR F,etal.Numerical Modeling ofWater Quality and Sediment Related Process[J].Ecological Modeling,2007,201(3/4):385-397.
[8]付长营,陶 敏,方 涛,等.三峡水库香溪河库湾沉积物对磷的吸附特征研究[J].水生生物学报,2006,30(1):31-36.(FU Chang-ying,TAO Min,FANG Tao,etal.Characteristics of Phosphorus Sorption in Sediment of Three Gorges Reservoir Xiangxi Bay[J].Acta Hydrobiologica Sinica,2006,30(1):31-36.(in Chinese))
[9]CAO Zhi-jing,ZHANG Xin-bao,AINan-shan.Effect of Sediment on Concentration of Dissolved Phosphorus in the Three Gorges Reservoir[J].International Journal of Sediment Research,2011,26(1):87-95.
[10]ZHOU Ai-min,TANG Hong-xiao,WANG Dong-sheng.Phosphorous Adsorption on Natural Sediments:Modeling and Effects of pH and Sediment Composition[J].Water Resources,2005,(39):1245-1254.
[11]WANG Y,SHEN Z Y,NIU J F,et al.Adsorption of Phosphorus on Sediments from the Three-Gorges Reservoir(China)and the Relation with Sediment Compositions[J].Journal of Hazardous Materials,2009,(162):92-98.
[12]李 健.香溪河水华数值模拟研究[D].北京:清华大学,2012.(LI Jian.Numerical Simulation of Xiangxi River Algal Blooms[D].Beijing:Tsinghua University,2012.(in Chinese))
[13]张 超.非点源污染模型研究及其在香溪河流域的应用[D].北京:清华大学,2008.(ZHANG Chao.Distributed Nonpoint Sources Pollution Modeling and Its Application in Xiangxi Watershed[D].Beijing:Tsinghua University,2008.(in Chinese))
[14]王 颖,沈珍瑶,呼丽娟,等.三峡水库主要支流沉积物的磷吸附-释放特性[J].环境科学学报,2008,28(8):1654-1661.(WANG Ying,SHEN Zhen-yao,HU Li-juan,etal.Adsorption and Release of Phosphorus from Sediments from the Main Branches of the Three-Gorges Reservoir[J].Acta Scientiae Circumstantiae,2008,28(8):1654-1661.(in Chinese) )
(编辑:陈 敏)
Calculation Formulas for Particulate and Dissolved Phosphorus Concentrations
LIJian,JIN Zhong-wu,YANGWen-jun
(River Department,Yangtze River Scientific Research Institute,Wuhan 430010,China)
The adsorption-desorption between phosphorus and suspended sediment particles in rivers or lakeswould influence the cycling process ofwater quality components.In this research,the calculation formulas for particulate phosphorus(PP)and dissolved phosphorus(DP)concentrations were deduced based on the classic Langmuir equation and themodified Langmuir equation,respectively.Furthermore,the experimental data and in-situ observed data of phosphorus and suspended sediment in XiangxiRiverwere used to verify the deduced formulas,and the calculated resultswere well consistentwith the observed data.When suspended sediment concentration was low,the linear equation could work well,butwhen suspended sediment concentration was relatively high,the deduced formula needs be used,especially when adsorption and desorption coexisted,the formula deduced bymodified Langmuir Equation needs be used.The research results could be applied for water quality and ecologicalmodeling.
suspended sediment;particulate phosphorus;dissolved phosphorus;concentration;adsorption-desorption;Xiangxi River
P342.3;X502
A
1001-5485(2015)01-0033-06
10.3969/j.issn.1001-5485.2015.01.007
2013-09-03;
2013-10-08
国家自然科学基金青年基金项目(51309021)
李 健(1984-),男,安徽金寨人,工程师,博士,研究方向为水生态环境数值模拟,(电话)15827130784(电子信箱)lijian_cky@hotmail.com。

