长江干流重庆主城河段造床流量计算

楚万强，李永丽，谢 龙

(1.黄河水利职业技术学院，河南 开封 475003；2.江苏省交通科学研究院股份有限公司，江苏 南京 210017)



长江干流重庆主城河段造床流量计算

楚万强1，李永丽1，谢 龙2

(1.黄河水利职业技术学院，河南 开封 475003；2.江苏省交通科学研究院股份有限公司，江苏 南京 210017)

为反映长江干流重庆主城河段河道特性，确定出造床流量，根据长江上游水文局1961—2007年的实测资料，利用马卡维耶夫法和频率分析法分别对造床流量进行了计算，通过对二者方法及计算结果的综合分析，推荐了寸滩河段及玄坛庙河段的造床流量值。通过多元回归分析，建立了造床流量与水力参数的经验公式，其结果可为各河段的航道治理以及同类型河段造床流量的确定提供参考。

航道工程；造床流量；频率分析

重庆主城河段干流段上起大渡口(距坝里程644.5 km)，下至铜锣峡(距坝里程598 km)，河段长36 km，流域面积2.85 km2。该河段地处长江上游丘陵宽谷河段,平面形态呈连续弯曲状，航道内礁石林立，滩险密布，航道条件极为复杂[1]。近十年来，随着西部大开发战略的实施，重庆地区水上运输需求日益旺盛，为了满足水运发展需求，交通运输部提出了“深下游、畅中游、延上游”的建设发展思路[2]，为此需要对目前上游部分滩险河段进行整治，切实提高其航道通过能力。在河道整治规划中，造床流量作为主要参数之一，常用来作为设计河流常年的断面和平面形态的依据。因此笔者主要研究该河段造床流量的特性及计算方法，为治理此类河段提供理论基础。

1 造床流量计算方法分析

造床流量Qf是造床强度与多年流量过程综合造床强度相等的单一流量[3]，它是河道演变中最重要的自变量，决定了河流的平均形态，对河床的塑造起着重要作用。由于造床强度是一个很模糊的概念，造床流量的计算很多，目前代表性的有以下几种方法。

1.1 马卡维耶夫法

前苏联学者马卡维耶夫认为河床的变化与造床强度及造床历时有关[4]。由于床面变化是河段输沙作用的结果，因此可用输沙率来表征造床强度；且造床历时可用该级强度对应的流量所占流量过程的频率确定[5]，因此将造床作用定义为：

G=QmPJ

(1)

式中：Q为流量；m为变指数，由Q～Qs的关系确定(Qs为输沙率)；J为水面比降；P为本级流量的频率密度，P=ΔP/ΔQ，ΔQ为流量分级，ΔP为ΔQ对应的频率。

1.2 频率分析法

钱宁[6]提出：“河床的演变不仅取决于上游来水来沙的绝对数量，还与它们的过程有关。”在对长江上游顺直河段多年数据统计、分析的基础上，钱宁认为造床流量接近于4年(P= 25%) 一遇的洪峰流量。

1.3 平滩流量法

韩其为[4]分析认为：河道水流从枯水流量逐渐增大的过程中，流速和床面切应力不断增大，造床作用增强，而水流漫滩后，水流分散且边滩阻力较大，主槽造床作用减弱，因此平滩流量法把河道水位与河漫滩齐平时水位对应的流量作为造床流量。

由于此法适用于河槽宽浅、河漫滩宽阔(一般洪水漫滩长度可达到主槽的5～10倍)的冲击河段，而重庆河段属大比降山区河流，河槽断面主要呈“V”字形峡谷，滩唇高程与水位-流量关系不易准确标定，因此笔者不考虑此计算方法。

2 长江干流重庆主城河段造床流量计算

笔者根据长江上游水文局对长江干流寸滩、玄坛庙水文站1961—2007年的实测资料，对各方法分别进行计算。

2.1 马卡维耶夫法

2.1.1 计算步骤

将实测的日均流量汇总，找出流量值的最大值与最小值，以500 m3/s为步长划分流量区间，确定每一流量区间内的概率P，并计算每一区间内流量的加权平均值Q*；建立流量Q与坡降J的曲线关系，查找每一级平均流量Q*所对应的比降；建立水流输沙率Qs与流量Q的指数关系，确定变指数m的取值；然后根据式(1)计算每一级流量的造床作用，拟合G-Q的关系曲线，曲线峰值(即G的最大值)对应的流量即为造床流量。

2.1.2Q-J关系确定

天然河流中，由于水面比降难以施测，可根据该河段附近的两个水文站，其实测的水位差值除以距离即为水面坡降。寸滩河段的比降采用寸滩站和铜锣峡站的实施数据，玄坛庙河段的比降采用玄坛庙站和鹅公岩站的实测数据。

通过实测数据拟合各站流量-水面比降关系，其曲线关系如图1。

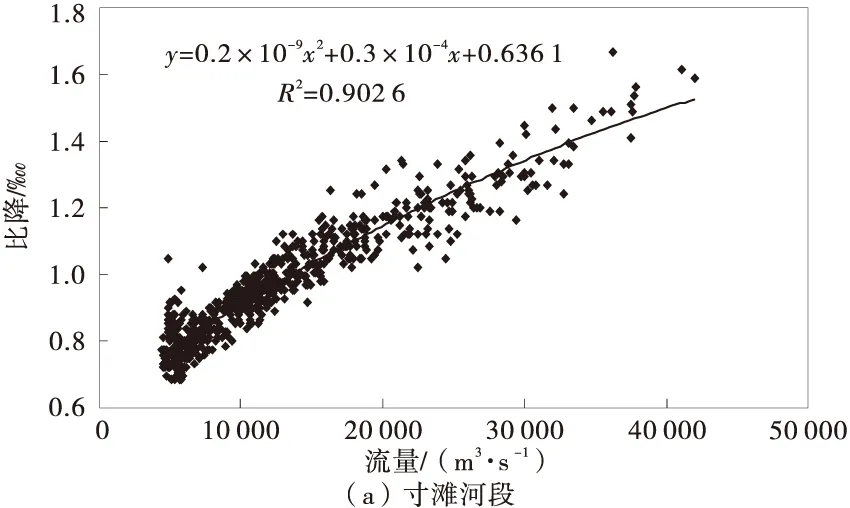
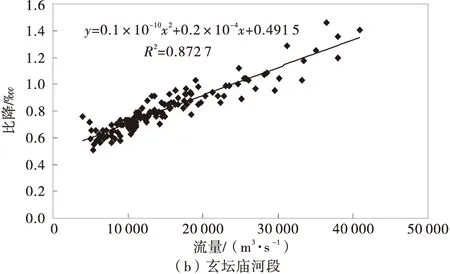
图1 Q-J曲线关系 Fig.1 Q-J curve relation

2.1.3Qs-Q关系确定

由于泥沙运动的能量来源于水流的切应力[7]，因此马卡维耶夫认为输沙率Qs可用流量Q和比降J来表征，通常情况下输沙率随水面比降变化较小，因此可忽略水面比降变化对其影响。分别建立各河段Qs-Q的关系(图2)，可确定寸滩河段变指数m=2.316，玄坛庙河段的m=2.612。

马卡维耶夫推荐冲积平原河流m=2，对比可知山区大比降河流输沙率受流量影响要大于冲积平原河流。

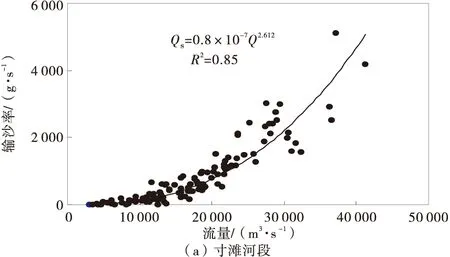
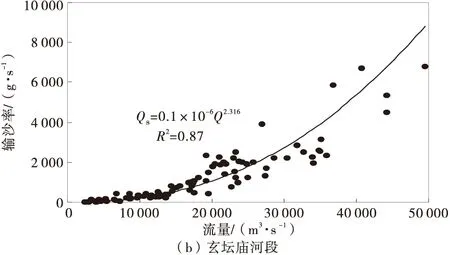
图2 Qs-Q曲线关系Fig.2 Qs-Q curve relation

2.1.4G-Q曲线拟合

根据式(1)分别计算各河段每级流量的造床作用G，点绘成曲线，如图3。从图中可知寸滩河段的造床流量为16 500～17 000 m3/s，玄坛庙河段的造床流量为14 500～16 000 m3/s。对比可知，在重庆主城河段，支流入汇后(寸滩河段)的造床作用要略大于入汇前(玄坛庙河段)。

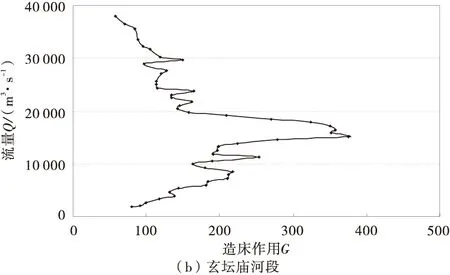
图3 G-Q曲线关系Fig.3 G-Q curve relation

2.2 频率分析法

根据洪水经验频率计算公式〔式(2)〕[8]，采用皮尔逊Ⅲ型水文频率分布曲线[9]，绘制各河段的洪峰流量经验频率曲线(图4)，对应可查出寸滩站的4年(P=25%) 一遇的洪峰流量为17 500 m3/s，即为造床流量，玄坛庙站的造床流量为13 800 m3/s：

(2)

式中：P(i)为样本中流量≥i的频率；m为样本中流量≥i的次数；n为样本总容量。

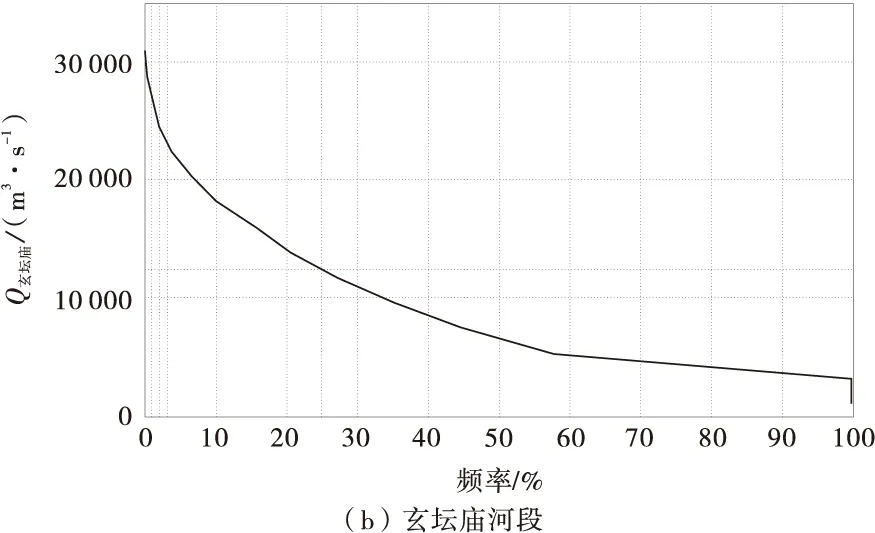
图4 P-Q曲线关系Fig.4 P-Q curve relation

3 计算结果分析

由于频率分析法是在对长江上游山区河流的统计基础上建立的经验公式，与实际值会有一定的误差，且大比降山区河流不同河段地形、边界条件差异较大，该经验公式在应用到具体河段时也会有一定的误差。马卡维耶夫法则较全面的从造床强度和造床历时两方面考虑了水流对河床的切应力作用[10]，通过具体河段的实测数据进行计算，误差相对较小。两种方法的计算结果如表1。

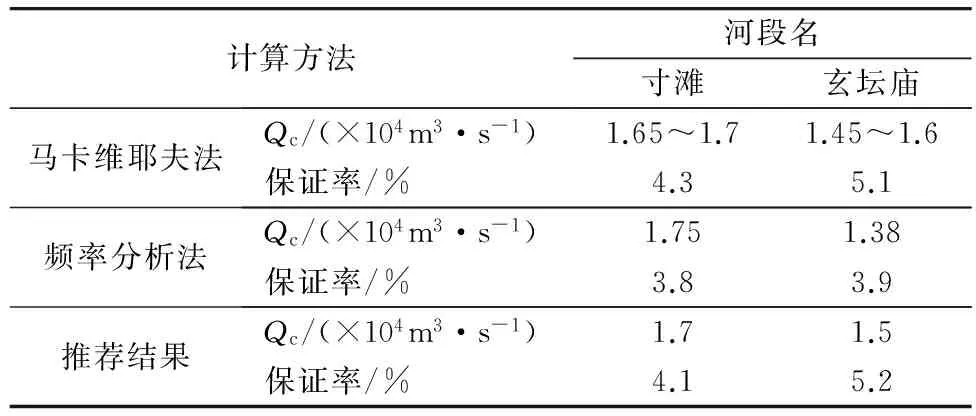
表1 长江干流重庆主城各河段造床流量计算

由表1数据看出，这两种计算方法所得结果较为相近，据分析，综合来看用马卡维耶夫法所得结果误差较小，因此推荐在参考马氏法计算结果基础上，寸滩河段的造床流量为17 000 m3/s，玄坛庙河段的造床流量为15 000 m3/s，前者(下游)略大于后者(上游)，这主要是因为两河段之间有嘉陵江支流入汇，流量增大所致。

4 长江干流重庆主城河段造床流量特性分析

河段的冲淤变化是水流与泥沙相互作用的结果，由河道的来水来沙情况、河床边界条件、河段输沙能力等因素决定。对具体河段来说，输水输沙是紧密相连的，因此可用某一特征流量来表征河段长期水沙条件变化，该特征流量即为造床流量。另外，水流对河床的造床作用与上游来水情况相关，反映河段来水情况的水力参数主要有多年平均流量、多年汛期平均流量等，这些特征参数与造床流量必定存在一定的联系。因此可将造床流量定义为：

(3)

式中：Q年为多年平均流量；Q汛为多年汛期平均流量；a，b，c，d，e均为待定系数。

根据实测资料，采用麦夸特迭代法对式(3)进行多元回归分析，可得寸滩河段的造床流量：

Qf寸滩=0.56Q年0.86+0.33Q汛0.53+172.2

(4)

玄坛庙河段的造床流量：

Qf玄坛庙=0.77Q年0.71+0.41Q汛0.60+23.62

(5)

5 结 论

1)笔者针对大比降山区河段，根据1961—2007年的实测资料，分别利用马卡维耶夫法和频率分析法对长江干流寸滩和玄坛庙河段的造床流量进行了计算，通过两种方法及其计算结果的对比推荐寸滩河段的造床流量为17 000 m3/s，玄坛庙河段的造床流量为15 000 m3/s。为大比降山区河流造床流量的确定提供了参考。

2)用造床流量这一特征流量来表征河段长期水沙变化，用水力参数来表征河段多年来水情况，分析这两者的相关性，并用多元线性回归确定待定系数，建立长江干流重庆主城河段造床流量的经验公式，可为科学预测该河段的造床流量提供参考。

[1] 谢龙.三峡变动回水区末端段复合水动力条件分析及对泥沙输移的影响[D].重庆:重庆交通大学,2013. Xie Long.Study on Compound Hydrodynamic Conditions in terminal of Fluctuating Backwater Reach of Three Gorge Reservoir and Its Influence of Sediment Transport [D].Chongqing:Chongqing Jiaotong University,2013.

[2] 谢龙,杨胜发,付旭辉,等.天白水电站溢洪道弯曲段流态优化试验[J].重庆交通大学学报:自然科学版,2013,32(2):310-312. Xie Long,Yang Shengfa,Fu Xuhui,et al.Flow pattern optimization experiment of bending section of Tianbai hydroelectric station spillway [J].Journal of Chongqing Jiaotong University:Natural Science,2013,32(2):310-312.

[3] 赵志舟,吕娜.长江上游急弯分汊河段通航整治汊道选择[J].水运工程,2009(10):112-117. Zhao Zhizhou,Lv Na.Regulation channel choice for the pebble shoals of branching reach with sharp bend shoal on the upper reach of the Yangtze River [J].Port & Waterway Engineering,2009(10):112-117.

[4] 韩其为.黄河下游输沙及冲淤的若干规律[J].泥沙研究,2004(3):1-13. Han Qiwei.Some rules of sediment transportation and deposition-scouring in the lower Yellow River [J].Journal of Sediment Research,2004(3):1-13.

[5] Colosimo C,Copertino V A,Vehri M.Friction factor evaluation on gravel-bed rivers [J].Journal of Hydraulic Engineering,1988,114(8):861-869.

[6] 钱宁.河床演变学[M].北京:科学出版社,1989. Qian Ning.River Bed Evolution Learning [M].Beijing:Science Press,1989.

[7] 张红武,张俊华,卜海磊,等.试论推移质输沙率公式[J].南水北调与水利科技,2011,9(6):140-145. Zhang Hongwu,Zhang Junhua,Bu Hailei,et al.Discussion of bed-load transport equations [J].South-to-North Water Diversion and Water Science & Technology,2011,9(6):140-145.

[8] 詹道江,徐向阳,陈元芳.工程水文学[M].4版.北京:中国水利水电出版社,2010. Zhan Daojiang,Xu Xiangyang,Chen Yuanfang.Engineering Hydrology [M].4th ed.Beijing:China WaterPower Press,2010.

[9] Wilcock P R.Critical shear stress of natural sediments [J].Journal of Hydraulic Engineering,1993,119(4):491-505.

[10] 李双江,谢龙.长江上游塘土坝河段水流特性及河床演变分析[J].重庆交通大学学报:自然科学版,2013,32(4):673-676. Li Shuangjiang,Xie Long.Riverbed evolution and water flow characteristics of Tangtuba Reach in the upper stream of Yangtze Rive [J].Journal of Chongqing Jiaotong University:Natural Science,2013,32(4):673-676.

Calculation of Dominant Discharge of Chongqing Urban Reach in Yangtze River Main Stream

Chu Wanqiang1, Li Yongli1, Xie Long2

(1. Yellow River Conservancy Technical Institute, Kaifeng 475003, Henan, China; 2. Jiangsu Transportation Institute, Nanjing 210017, Jiangsu, China)

To reflect the channel characteristics of Chongqing urban reach of the Yangtze River and to determine the discharge of forming the river bed, the dominant discharge was calculated by Makovieve method and frequency analysis method, which was based on the measured data of the Yangtze River committee hydrographic office from 1961 to 2007. Through the comprehensive analysis on the calculation results of the above two method, the bed-building discharge of Cuntan reach and Xuantanmiao reach was recommended. Finally, the empirical formula between the bed-building discharge and the hydraulic parameters was established through the multiple regression analysis, and its results could offer the reference for the channel governance of reaches and the determination of the dominant discharge of the reaches with the same kind.

waterway engineering; dominant discharge; frequency analysis

10.3969/j.issn.1674-0696.2015.02.15

2013-01-05；

2013-12-05

国家自然科学基金项目(50579041)

楚万强(1976—)，男，河南洛阳人，讲师，硕士，主要从事水利水电工程方面的研究。E-mail: 287109894@qq.com。

TV143

A

1674-0696(2015)02-069-03