地下工程围岩稳定性的非线性强度评价指标

吴恒滨，张学富

(1.重庆三峡学院 土木工程学院，重庆404100；2. 重庆交通大学 土木建筑学院，重庆 400074)



地下工程围岩稳定性的非线性强度评价指标

吴恒滨1，张学富2

(1.重庆三峡学院 土木工程学院，重庆404100；2. 重庆交通大学 土木建筑学院，重庆 400074)

通过分析Mohr-Coulomb和Drucker-Prager屈服准则现有的围岩屈服评价指标，提出了以I1，J2为基准的屈服评价指标。在线性屈服准则中两者是等价的，在非线性强度准则中，以I1为基准的屈服评价指标较小，建议采用以J2为基准的屈服评价指标。对于以J2为基准的广义Hoek-Brown准则的求解存在着数学上的困难，将其转换为等效强度参数代入Mohr-Coulomb准则屈服评价指标表达式，进而对围岩稳定性进行屈服评价。算例分析表明：隧道开挖支护后的等效塑性应变和屈服评价指标规律一致，验证了该屈服评价指标的正确性；隧道屈服评价指标可以直观的显示隧道应力集中程度及围岩安全状态的演绎规律，能够更准确的描述围岩受力状态。

岩土工程；围岩稳定性；屈服评价指标；Hoek-Brown准则

0 引 言

地下工程的开挖会导致围岩应力重分布，并产生应力集中，若围岩应力大于岩体强度，会使洞室产生塑性或破坏。与边坡工程不同，地下工程不能给出定量评价围岩稳定性的安全系数，从而导致地下工程在优化设计及指导施工方面存在着诸多问题。张黎明，等[1]和杨臻，等[2]试图通过强度折减技术给定地下工程安全系数，仍处于探索阶段。现阶段，地下工程围岩稳定性主要依靠现场监测数据及数值计算结果进行定性-半定量判断。根据监测资料，建立围岩的位移标准及允许变形值，借此了解围岩的力学性态较为直观且易于实施，然而，随着地下工程结构和围岩性态越来越复杂，使得围岩稳定要求的极限位移的确定更加困难[3-4]。通过数值计算，可以得到开挖过程中围岩变形特征及支护的受力状态，结合现场监测数据对地下工程信息化设计与施工具有重要指导意义。而围岩在集中应力作用下的损伤程度及安全状态的演绎规律尚不能准确显现出来[5]。

为此，诸多学者对地下工程围岩安全分区即屈服指标评价技术进行研究，尝试更准确的描述在开挖过程中围岩的受力状态。潘昌实[6]参照Mohr-Coulomb准则计算得出高斯点的强度发挥系数；杜丽惠，等[7]在反应单元材料的非线性特征时引入了破坏接近度的概念；沈才华，等[8]结合ANSYS软件根据等效应力和屈服应力之比来定量表述隧道围岩受力状态；张传庆[5]根据Mohr-Coulomb屈服准则在空间应力偏平面性质，提出了一个屈服接近度(Yield Approach Index，YAI)的新概念；李树忱，等[9]根据工程安全系数的定义，建立了隧道围岩最小安全系数法模型；蒋青青[10]将广义Hoek-Brown准则的等效Mohr-Coulomb准则抗剪强度参数进行点安全系数分析；吴恒滨，等[11-12]引入屈服接近度的概念对小净距大断面隧道合理净距进行研究。

综上所述，在地下工程围岩屈服指标评价中，表达式多样且应用多有局限性。根据前述工作成果，对屈服准则在应力空间中的一般表达式分析，提出以I1，J2为基准的地下工程围岩稳定性的非线性强度屈服评价指标，进一步通过工程实例进行验证。

1 围岩屈服评价指标

1.1 围岩屈服评价指标

对于一般受力下的岩土，所考虑的任何一个受力面，其极限抗剪强度通常可以用Coulomb定律表示：

τ=c-σntanφ

(1)

式中：τ为极限抗剪强度；σn为受剪面上的法向应力，以拉为正；c，φ分别为岩土材料的黏聚力及内摩擦角。

将式(1)推广为平面应力状态的Mohr-Coulomb条件：

(2)

式中：σ1，σ2，σ3分别为最大主应力、中主应力和最小主应力。

潘昌实[6]参照式(2)给出了材料强度发挥系数(S.M.F.)公式：

(3)

考虑到最小主应力符号问题，在式(3)中对σ1+σ3取绝对值。当S.M.F.≥1时，可认为材料已经进入塑性状态。

式(2)若用应力张量的第一不变量I1，应力偏量的第二不变量J2，应力洛德角θσ表示，即可写成应力空间的一般屈服条件：

(4)

张传庆[5]将空间应力状态下一点沿最不利路径到屈服面的距离与相应的最稳定参考点在相同罗德角方向上沿最不利应力路径到屈服面的距离之比定义为屈服接近度(YAI)，其表达式如式(5)：

(5)

式(5)的物理意义基本明确，认为屈服接近度在[0,1]之间。其中：等于0时，发生屈服；靠近1时，则相对安全。

同时，还给出了Drucker-Prager准则的屈服接近度公式：

(6)

式中：α,k分别为岩土材料黏聚力和内摩擦角相关系数。

根据Drucker-Prager准则[13]，式(7)给出了屈服接近度η的定义：

(7)

沈才华，等[8]根据ANSYS软件提供的计算过程给出了等效应力和屈服应力比值判断屈服评价指标的方法：

(8)

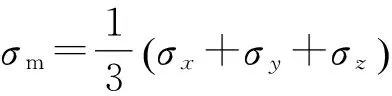
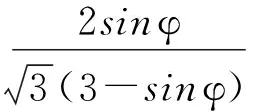
由式(8)可知，式中β，σy，3σm分别即为式(7)中的α，k，I1，将σe中式子部分稍加推导：

(9)

则式(9)和式(7)其实是等价的。

李树忱，等[9]借助工程中安全系数的概念，利用Mohr-Coulomb和Drucker-Prager强度准则，建立基于单元的安全系数Fs：

(10)

式(10)与式(3)区别在于主应力符号不同，两者都通过算例验证了其正确性。式(10)与式(8)则区别较为明显，其比值的物理意义有所变化。

1.2 非线性强度评价指标

根据前述工作成果，可认为材料屈服指标可以I1，J2为基准来进行评价。接下来主要介绍材料受剪破坏屈服情况，受拉屈服较为简单，可以直接用拉应力和岩体抗拉强度之比确定屈服程度。根据塑性理论可知，I1可以用来描述该点在偏平面上的投影点到原点的距离，而J2可以用来描述在偏平面上该点到中心处距离，它与偏平面上剪应力有关。任意一点的空间应力可以分解为应力张量的形式：

(11)

则屈服准则可以转化为用I1，J2，θσ这3个变量表示，其中Mohr-Coulomb准则可变换为式(4)，对式(4)进行变换：

(12)

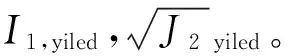
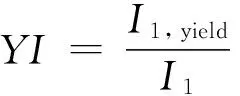
(13)

将式(4)代入式(13)即得Mohr-Coulomb准则屈服评价指标：

(14)

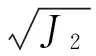
E．Hoek，等[14]于2002年提出经验的广义Hoek-Brown准则：

(15)

其中：σci为岩体单轴抗压强度；mb,s,a分别为经验参数。

将式(15)代入式(11)中，可得广义Hoek-Brown准则在应力空间中的表达式：

(16)

则基于I1的广义Hoek-Brown准则的屈服评价指标：

(17)

(18)

式中：σ3max为等效条件下最小主应力上限值。

柳群义，等[15]根据Hoek-Brown准则的等效抗剪强度参数代入式(5)屈服接近度进而对隧道稳定性进行分析。蒋青青[10]将Hoek-Brown准则的等效抗剪强度参数代入式(10)进行点安全系数分析。而式(10)为Drucker-Prager准则屈服评价指标公式，将等效Mohr-Coulomb准则参数代入Drucker-Prager准则屈服表达式，无疑会进一步加大Hoek-Brown准则屈服判断的误差。笔者建议直接采用式(17)或将式(18)算出的等效Mohr-Coulomb准则参数代入式(14)可得到围岩屈服评价指标。

笔者建议的方法较文献[5]提出的屈服接近度计算比较简单，非常容易推广到其他屈服准则，无需进行复杂的公式推导。对比现有研究成果，式(3)和式(10)应用具有局限性，式(5)和式(6)较为复杂复杂，笔者建议的方法具有明确的物理意义和良好的适用性，在岩土工程安全性评价方面显得更具有优势。

3 算例分析

某隧道断面为三心圆，半径为5.6m。为验证前述理论正确性，对该隧道进行弹塑性分析。模型共划分54 340个单元(图1)。隧道围岩按均质弹塑性考虑，屈服准则采用广义Hoek-Brown准则。支护采用复合式衬砌，按弹性材料考虑(材料基本物理力学参数见表2)。模型边界左右为100m，上边界取至地表，下边界取40m，隧道纵向长度取50m。

图1 数值计算模型Fig.1 Numerical analysis model

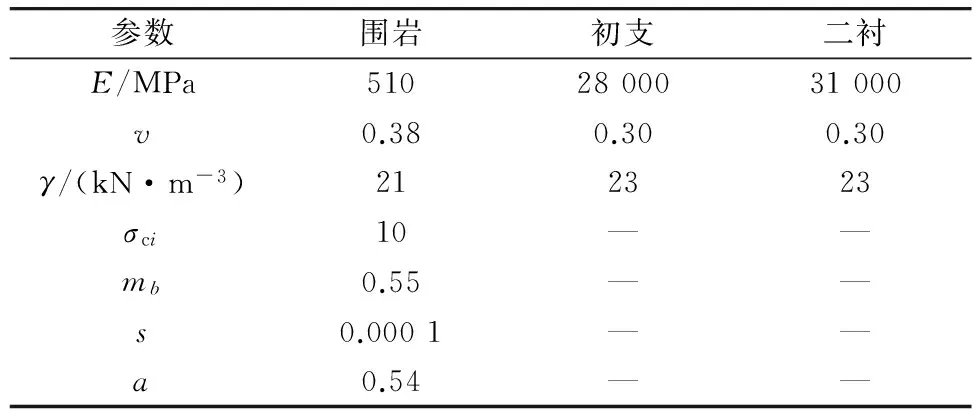
参数围岩初支二衬E/MPa5102800031000v0.380.300.30γ/(kN·m-3)212323σci10——mb0.55——s0.0001——a0.54——

鉴于FLAC3D软件前处理功能的缺陷，采用ANSYS软件建立有限元模型，然后导入FLAC3D对该隧道进行快速有限差分计算，并将围岩材料参数转换为等效Mohr-Coulomb准则强度参数，得到黏聚力为0.136 MPa，内摩擦角为21.7°。通过编制内部FISH命令，得到隧道开挖支护后的塑性应变和围岩屈服评价指标，将结果输入后处理软件Surfer绘制图形见图2、图3。

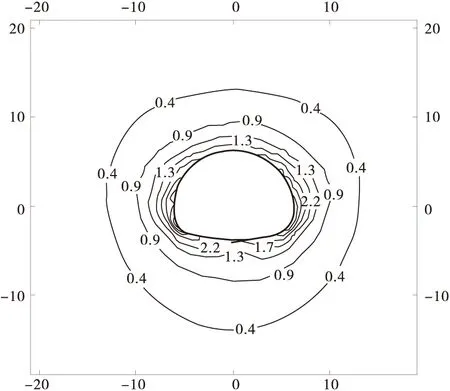
图2 隧道围岩塑性应变με/103

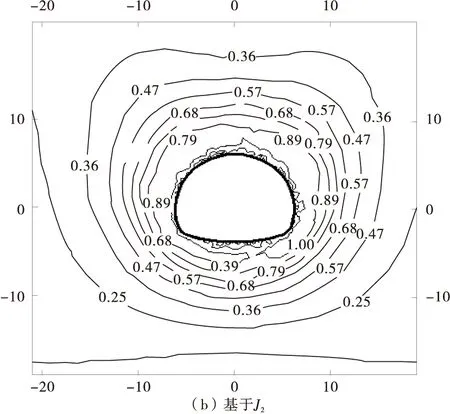
图3 隧道围岩屈服评价指标Fig.3 The YI of tunnel surrounding rock after support

从图2、图3可以看出，隧道围岩屈服评价指标大致呈圆形向外扩散，在隧道拱腰处较大，在仰拱处稍小一些。对比隧道围岩塑性应变图，其规律相似，可以验证笔者建议屈服评价指标的正确性。从应力空间图形知，等效Mohr-Coulomb准则强度参数和广义Hoek-Brown准则参数相比，在地应力区较为保守，在高应力区偏于危险。尽管基于I1得到的屈服评价指标较小，但由于围岩材料经过等效转换后，得到的屈服评价指标无法比较。

此外，围岩屈服评价指标整体不大，复合式衬砌支护可以满足工程的要求。隧道屈服评价指标可以直观的显示隧道应力集中程度及围岩安全状态的演绎规律，能够更准确的描述围岩受力状态，为地下工程围岩稳定性判定提供参考依据。

4 结 语

地下工程围岩稳定性判定是岩体力学的一项重要内容，它对指导设计与施工具有重要的工程价值。针对目前地下工程围岩稳定性判定存在的问题，以Mohr-coulomb准则和Drucker-Prager准则为例，对常用屈服准则屈服评价指标表达式进行分析，并提出以I1，J2为基准的屈服评价指标，可以非常方便的用于数值计算程序编制。从两者物理意义可知，以I1为基准的屈服评价指标较小，建议一般情况下以J2为基准，得到的围岩屈服评价较为保守。

对于非线性屈服准则，推导了广义Hoek-Brown准则屈服评价指标，可以直接通过以I1为基准得到屈服评价指标。对于以J2为基准的广义Hoek-Brown准则的显示解存在数学上的困难，通过等效强度参数，代入Mohr-Coulomb准则屈服评价指标评价指标，进而对围岩稳定性进行判定。

最后，通过工程算例分析，验证了笔者建议围岩稳定性屈服评价指标的正确性，隧道屈服评价指标可以直观的显示隧道应力集中程度及围岩安全状态的演绎规律，能够更准确的描述围岩受力状态，为地下工程围岩稳定性判定提供参考依据。

[1] 张黎明,郑颖人,王在泉,等.有限元强度折减法在公路隧道中的应用探讨[J].岩土力学,2007,28(1):97-106. Zhang Liming,Zheng Yingren,Wang Zaiquan,et al.Application of strength reduction finite element method to road tunnels[J].Rock and Soil Mechanics,2007,28(1):97-106.

[2] 杨臻,郑颖人,张红,等.岩质隧洞支护结构设计计算方法探索[J].岩土力学,2009,(增刊1):148-154. Yang Zhen,Zheng Yingren,Zhang Hong,et al.Exporting computational method of designing the supporting structure of rock tunnel[J].Rock and Soil Mechanics,2009,(Sup1):148-154.

[3] 高峰,薛佃立.大跨偏压软弱围岩双连拱隧道施工过程研究[J].重庆交通大学学报:自然科学版,2014,33(2):30-34. Gao Feng,Xue Dianli.Double-arch tunnel construction in large span bias weak surrounding rock[J].Journal of Chongqing Jiaotong University:Natural Science,2014,33(2):30-34.

[4] 靳宝成.杨河隧道的变形控制标准与支护措施的关系[J].重庆交通大学学报:自然科学版,2013,32(2):224-228. Jin Baocheng.Relationship between deformation control standard and supporting measures of yanghe tunnel[J].Journal of Chongqing Jiaotong University:Natural Science,2013,32(2):224-228.

[5] 张传庆.基于破坏接近度的岩石工程安全性评价方法的研究[D].武汉:中国科学院武汉岩土力学研究所,2006. Zhang Chuangqing.Study on method of safety evaluation for rock engineering based on failure approach index[D].Wuhan:Institute of Rock and Soil Mechanics,Chinese Academy of Sciences,2006.

[6] 潘昌实.隧道力学数值方法[M].北京:中国铁道出版社,1995. Pan Changshi.Numerical Analysis Method for Tunnels[M].Beijing:China Railway Publishing House,1995.

[7] 杜丽惠,黄丽清.考虑围岩蠕变特性的轴对称有限元非线性分析[J].水利学报,2001(1):85-89. Du Lihui,Huang Liqing.The nonlinear axisymmetric finite element method for analysis of surrounding rock in consideration of creeping [J].Journal of Hydraulic Engineering,2001(1) :85-89.

[8] 沈才华,刘松玉,童立元.卵砾石土层大跨公路隧道初期支护优化研究[J].岩石力学与工程学报,2008,27(增刊1):2984-2989. Shen Caihua,Liu Songyu,Tong Liyuan.Primary-supporting optimization for large-span road tunnels in gravel deposit layers[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(Sup1):2984-2989.

[9] 李树忱,李术才,徐帮树.隧道围岩稳定分析的最小安全系数法[J].岩土力学,2007,28(3):549-554. Li Shuchen,Li Shucai,Xu Bangshu.Minimum safety factor method for stability analysis of surrounding rockmass of tunnel[J].Rock and Soil Mechanics,2007,28(3):549-554.

[10] 蒋青青.基于Hoek-Brown准则点安全系数的边坡稳定性分析[J].中南大学学报:自然科学版,2009,40(3):786-790. Jiang Qingqing.Stability of point safety factor of slope based on Hoek-Brown criterion[J].Journal of Central South University:Science and Technology,2009,40(3):786-790.

[11] 吴恒滨,张学富,周元辅,等.小净距大断面隧道合理净距研究[J].重庆交通大学学报:自然科学版,2010,29(1):63-68. Wu Hengbin,Zhang Xuefu,Zhou Yuanfu,et al.Reasonable spacing of closely spaced tunnels with large cross-section[J].Journal of Chongqing Jiaotong University:Natural Science,2010,29(1):63-68.

[12] 吴恒滨.小净距大断面隧道施工力学特性及长期稳定性研究[D].重庆:重庆交通大学,2009. Wu Hengbin.Study on Construction Mechanical Characteristics and Long-Term Stability of Large Section Tunnels with Closely Spaced[D].Chongqing:Chongqing Jiaotong University,2009.

[13] 任松,姜德义,刘欣荣,等.用3D-Sigma分析岩盐溶腔围岩地应力场[J].地下空间,2003,23(4):414-416. Ren Song,Jiang Deyi,Liu Xinrong,et al.Analysis on ground stress of rock salt cavern’s surrounding rock with 3D-Sigma[J].Underground Space,2003,23(4):414-416.

[14] Hoek E,Carranza-Torres C,Corkum B.Hoek-Brown failure criterion-2002 edition [C]//Proc.NARMS-TAC Conference.Toronto:University of Toronto Press,2002,1:267-273.

[15] 柳群义,朱自强,钟正强,等.基于Hoek-Brown准则的隧道围岩屈服接近度分析[J].岩土力学,2009,30(8):2447-2451. Liu Qunyi,Zhu Ziqiang,Zhong Zhengqiang,et al.Yielding approach index for surrounding rock mass of tunnel based on Hoek-Brown criterion[J].Rock and Soil Mechanics,2009,30(8):2447-2451.

Nonlinear Strength Yield Index of Surrounding Rock Stability for Underground Opening

Wu Hengbin1，Zhang Xuefu2

(1.College of Civil Engineering, Chongqing Three Gorges University, Chongqing 404100, China; 2. School of Civil Engineering & Architecture, Chongqing Jiaotong University, Chongqing 400074,China)

According to the analysis of surrounding rock yield index of the Mohr-Coulomb criterion and Drucker-Prager yield criterion, yield index (YI) is proposed based onI1andJ2. Both two methods are equivalent in the linear yield criterion,YIbased onI1is smaller thanJ2in nonlinear yield criterion, andYIbasedJ2is suggested. In view of the solution for generalized Hoek-Brown criterion exist mathematical difficulty, the generalized Hoek-Brown strength parameters are converted into the equivalent strength parameters, the yield evaluation of surrounding rock stability is further performed by substituting them into theYIexpression of Mohr-Coulomb criterion. In addition, numerical experiments are conducted, and the results show that the law of equivalent plastic strain are similar to that ofYIafter tunnel excavation and support, the accuracy ofYIis verified.YIof tunnel can show the degree of stress concentration and the interpretation law of surrounding rock safety state, describe more accurately the stress state of surrounding rock.

geotechnical engineering；stability of surrounding rock；yield index(YI)；Hoek-Brown criterion

10.3969/j.issn.1674-0696.2015.02.07

2013-11-21；

2014-07-09

国家自然科学基金项目(408307425)；科技部基金支撑项目(2011BAK12B03)

吴恒滨(1984—)，男，山东聊城人，讲师，博士，主要从事岩土工程方面的研究。E-mail:hbw8456@163.com。

TU451

A

1674-0696(2015)02-028-05