自由阻尼结构损耗参数的换算方法*

张安付， 闫孝伟， 盛美萍， 吴晴晴

(1.西北工业大学航海学院 西安，710072) (2.中国船舶工业系统工程研究院 北京，100094)

自由阻尼结构损耗参数的换算方法*

张安付1， 闫孝伟2， 盛美萍1， 吴晴晴1

(1.西北工业大学航海学院 西安，710072) (2.中国船舶工业系统工程研究院 北京，100094)

在自由阻尼结构理论的基础上，建立了不同自由阻尼结构之间的结构损耗因子换算关系。针对自由阻尼板、壳结构开展了阻尼测试，换算结果与测试结果一致性良好，验证了换算方法的有效性。同时开展了换算系数和误差放大因子的仿真分析。仿真结果表明：对于弹性模量较高的阻尼层，换算系数随厚度比变化较小，换算精度较高；对于弹性模量较低的阻尼层，换算系数随厚度比变化较大，换算精度较低。建议阻尼层比目标基材层厚，且换算基材厚度小于目标基材厚度的2倍。该换算方法可用于预估一些难以测量的自由阻尼结构损耗参数，为大型简单圆柱壳结构敷阻尼层后损耗参数的获得以及多种阻尼层在大型圆柱壳结构上抑振性能的评比提供参考方案。

阻尼材料; 结构损耗因子; 换算方法; 误差放大因子

引 言

阻尼材料利用了材料中的黏弹性将振动机械能转化为热能消耗掉，从而达到结构降噪隐身的目的。目前，各种型式的阻尼材料已经广泛运用于航空航天、汽车、船舶等诸多领域。在潜艇中，振动源比较集中的艇体、舱壁等都大量采用阻尼材料抑制振动。结构损耗因子是表征结构损耗能量的能力，是评价阻尼材料抑振性能的重要参数，近年来已经提出了多种测量方法[1-3]。多数文献只针对梁板壳结构的损耗因子进行了计算仿真分析[4-6]，对于大型结构损耗因子的实际测量主要是通过自由衰减法测量结构的T60来实现[7-8]。

目前，由于诸多因素的限制，直接测量潜艇艇壳敷设阻尼层后的结构损耗因子往往难以实现。潜艇艇壳是圆柱形状，在不同的频段内，其振动特性可以与钢板或缩比圆柱壳模型的振动特性等效[9]。在实际中，通常将阻尼层敷在钢板基材上，通过测量钢板基材敷阻尼层后的结构损耗因子来评价阻尼层的抑振性能。然而，潜艇艇壳和钢板基材之间存在着很大的尺寸和结构差别，会导致试验结构敷阻尼层后的结构损耗因子并不能真实表达潜艇艇壳敷阻尼层后的结构损耗因子。

基于上述问题，笔者在自由阻尼结构理论基础上[10]，建立不同基材之间结构损耗因子的换算关系，分析换算过程中的误差放大特性[11-12]，使用钢质圆柱壳和钢板作为试验基材，测试基材敷阻尼层前后的结构损耗因子并计算出换算值，通过换算值和试验值比较，验证所得换算关系的有效性，为在工程中推算自由阻尼圆柱壳结构损耗参数提供参考方案。

1 换算关系的建立

1.1 换算方法理论

A，B两类基材，如图1所示，厚度分别为Ha，Hb。A，B类基材上敷相同的C类阻尼层，厚度为Hc。

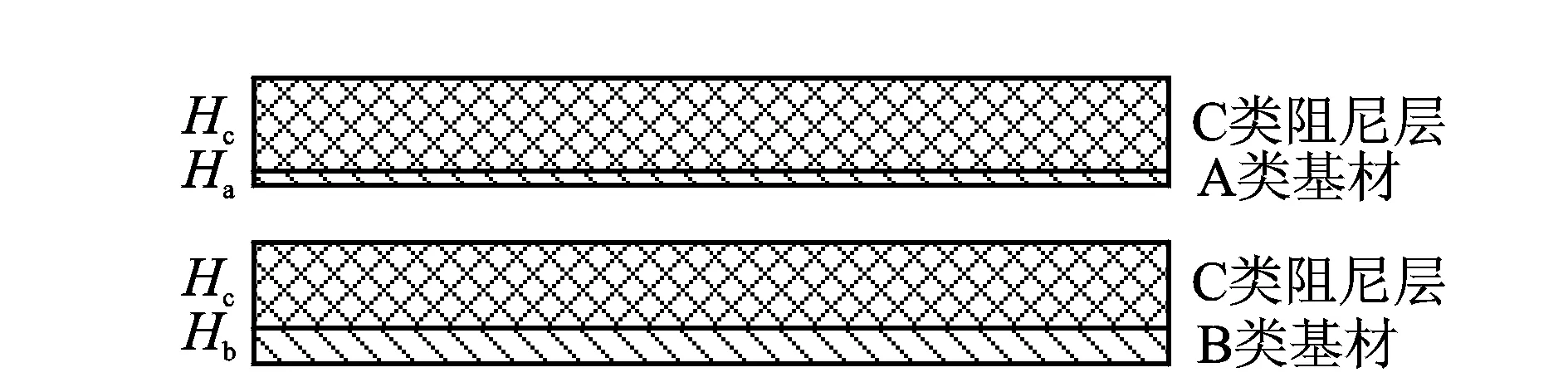
图1 两类自由阻尼结构模型Fig.1 Two kinds of unconstrained damping structure models

A类基材敷阻尼层后的结构损耗因子的表达式[10]为

(1)

B类基材敷阻尼层后的结构损耗因子的表达式为

(2)

其中：h1=Hc/Ha，h2=Hc/Hb，h1和h2为厚度比；e1=Ec/Ea，e2=Ec/Eb，e1和e2为弹性模量之比；Ea，Eb为A，B两类基材的弹性模量；Ec为阻尼材料的弹性模量；α1，α2为A，B两类基材自身的结构损耗因子；β为C类阻尼层的材料损耗因子。

将式(1)和式(2)相比，得到

(3)

式(3)表达了两类阻尼结构损耗参数之间的转换关系。可以看出两者的比值与厚度比、弹性模量比、材料损耗因子都有关系。

实际工程中，由于各种客观因素的存在，有些大型自由阻尼圆柱壳结构的损耗参数很难通过测试得到。对于这种情况，可以将式(3)变换成

(4)

通过测试、计算得到ηs2和比例因子λ就可以换算得到ηs1。A类基材可表示成目标基材，其敷设阻尼层后的损耗参数难以直接测量得到，如大型自由圆柱壳结构；B类基材可表示成换算基材，其敷设阻尼层后的损耗参数能方便测得，如钢板结构。式中，比例因子λ为ηs1与ηs2的比值，为式(3)的右边项。

这里的ηs2可以为自由阻尼钢板结构损耗因子。测试小型钢板结构损耗因子在实际中是可行的，而一些大型自由阻尼圆柱壳结构的损耗参数难以直接测得，因此，通过式(4)可以实现由测试得到的小型钢板结构损耗参数换算得到大型自由阻尼圆柱壳结构的损耗参数。

1.2 误差放大因子

由于式(4)中需要测量的参数有β，α1，α2，ηs24种损耗因子参数，这些参数的测试误差势必会影响到换算结果ηs1，因此有必要对式(4)进行误差分析。ηs1的绝对误差限ε(ηs1)可表示为

(5)

其中：ε(α1)，ε(α2)，ε(β)分别为测量目标基材、换算基材和阻尼层自身损耗参数产生的绝对误差限；ε(ηs2)为测量换算基材结构损耗参数产生的绝对误差限。

经误差估计的加减乘除运算后，绝对误差限ε(ηs1)可进一步表达为

(6)

其中

(7)

(8)

(9)

(10)

(11)

(12)

M2=1+2e1h1

(13)

(14)

M4=1+2e2h2

(15)

1.3 换算过程

虽然理论上目标基材和换算基材可以为不同材料，但是在实际操作中，为了消除因材料差异带来的不可预知的测试误差，需要设置换算基材的材料与目标基材相同，对于这种情况下的换算公式和误差放大因子，只需设置相关式中e1=e2即可得到。这里的目标基材的结构损耗因子α1和换算基材的结构损耗因子α2可能会因结构不同而有所差别，因此，各个公式里α1和α2不合并。

本研究换算方法有一定的工程应用背景。当需要知道一个大型圆柱壳在敷设阻尼层后的结构损耗因子，直接测试往往很难实施，本研究的换算方法可以提供一条间接获得大型圆柱壳结构损耗因子的途径。首先，通过测量钢板敷阻尼层前后的结构损耗因子得到参数α2和ηs2；其次，当阻尼层为无空腔的均匀阻尼材料时，可以使用特定的仪器(如黏弹性谱仪)或方法(如相位法)测量得到阻尼材料的材料损耗因子β；然后，通过测量大型圆柱壳的缩比模型获取结构的损耗因子α1(敷阻尼层前)，用于近似实际大型圆柱壳自身结构损耗因子;最后，经过式(4)的换算，即可得到大型圆柱壳的结构损耗因子ηs1。

若存在多个品种的阻尼层，可以设计相同数量的钢板基材和一个缩比模型，通过测试、换算，可得到大型圆柱壳敷设不同阻尼层的损耗参数，可以对各种阻尼层的减振效果进行判断，优选出抑振效果好的阻尼层。

本研究换算方法目前只能用于推算简单的相同结构，如典型梁、板、壳样品与梁、板、壳工程件之间的损耗因子的换算关系，不能推广到试样与实际不同的结构(如加筋)的损耗因子的推算。

2 试验验证

试验中，结构损耗因子采用自由衰减法测量，即对结构施加一定激励，停止激励后结构进行自由振动，自由振动的振幅衰减速度和阻尼直接相关。通过测量单次冲击后结构振动衰减60dB所需的时间，即混响时间T60，进而可以计算出结构损耗因子，计算公式为

(16)

其中：fn为第n个1/3倍频程的中心频率。

为检验本研究换算方法在实际工程中的有效性，设计了一个长度为3.6 m、直径为0.9 m、厚度为3 mm的钢质圆柱壳，一块1.3 m×1.1 m×5.5 m的钢质平板作为试验基材。阻尼层为橡胶，厚度为5 mm。弹性模量为2×107Pa，密度为1 140 kg/m3，材料损耗因子约为0.2。

由于本换算方法应用的背景为水下结构抑振性能的预估，故本次测试环境为可加压消声水罐，水罐内壁贴有吸声尖劈。使用钢索将结构自由悬挂于水罐中。试验采用冲击激励，激振系统为冲击装置，可为结构提供单次冲击，测试频率为50～5 000 Hz，测试系统如图2所示。

图2 测试系统示意图Fig.2 The diagram of measurement system

在试验中，采用冲击衰减法，测试了常压和2.0MPa两种压力下的4种结构，即钢板、自由阻尼钢板、钢壳、自由阻尼钢壳的结构损耗因子。部分通道实测时域数据如图3所示。

图3 4种结构振动衰减部分时域数据Fig.3 Part of time domain data of vibration attenuation for four structures

经式(4)计算，得到由自由阻尼钢板结构损耗因子换算到自由阻尼圆柱壳结构损耗因子的换算值，如图4所示。

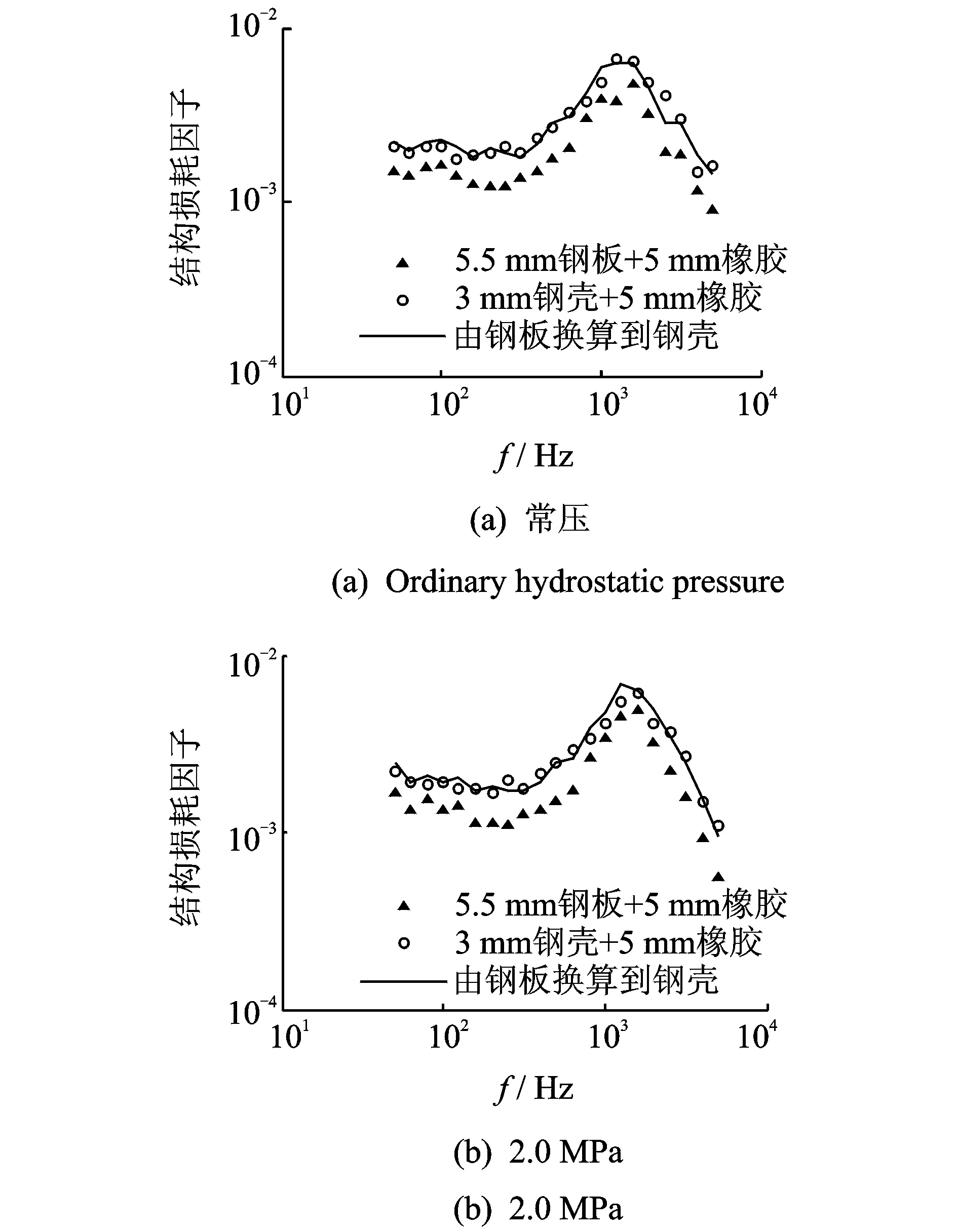
图4 水下钢板-钢壳结构损耗因子换算值与测试值比较Fig.4 The loss factor equivalent value and test value of steel plate-shell in water

通过由钢板换算得到的自由阻尼钢壳损耗因子换算值与自由阻尼钢壳的损耗因子测试值对比发现，两者的一致性很好，验证了本研究方法可以用于换算结构损耗因子。另外，通过图4中常水压和2.0 MPa水压的比较可以看出，水压对结构损耗因子的影响很小，没有显著影响本研究换算方法的精度。

测试中使用自由衰减法测试结构损耗因子，需要冲击装置在测试频段的每个1/3倍频程内都能激起足够多的振动能量，一般要求每个倍频程段内结构被激起的振动最高幅值比环境背景大20 dB。若结构在某个1/3倍频程内有模态，则结构在该倍频段内更容易被激起足够的振动能量，反之则不容易激起足够的振动能量。因此，钢板基材应通过特殊设计使得测试频段内每个1/3倍频程都存在模态，以减小信噪比不足带来的误差。被换算结构与钢板基材尺寸不同，模态分布不同，不能保证被换算结构测试频段内每个1/3倍频程都含有模态。被换算结构体积大，中高频段模态一般比较密集，满足有模态的条件，而在低频段可能由于某些1/3倍频程没有结构模态，导致能量不足，产生因信噪比不足引起的测试误差。

3 参数分析

对式(4)中的比例因子λ(e1,e2,h1,h1)进行仿真分析，这里取β=0.08，取6种弹性模量比，e1=e2=10-5，10-4，10-3，10-2，10-1和1，可以得到如图5所示的比例因子lgλ的数值随厚度比和弹性模量比变化的分布图，图中每个子图的横坐标和纵坐标均为阻尼层与基材的厚度比。同时，图5也可表示为绝对误差限ε(ηs2)前误差放大因子lgC4。

当图5显示为损耗因子比值lgλ时，黑色区域表示比例因子λ远大于1的区域；白色区域表示比例因子λ远小于1的区域；灰色区域表示λ在1附近。当lgλ=0时，λ=1，即ηs1=ηs2。从图5可以看出，对于弹性模量比较小的阻尼层，在h1，h2组成的坐标系中，比例因子λ值在比较大的区域内远离1，而且当换算基材和目标基材的厚度差距越大，λ值越远离1。对于弹性模量大的阻尼层，λ值在相当大的区域内接近1，当e1=e2=1时，λ值基本接近1。

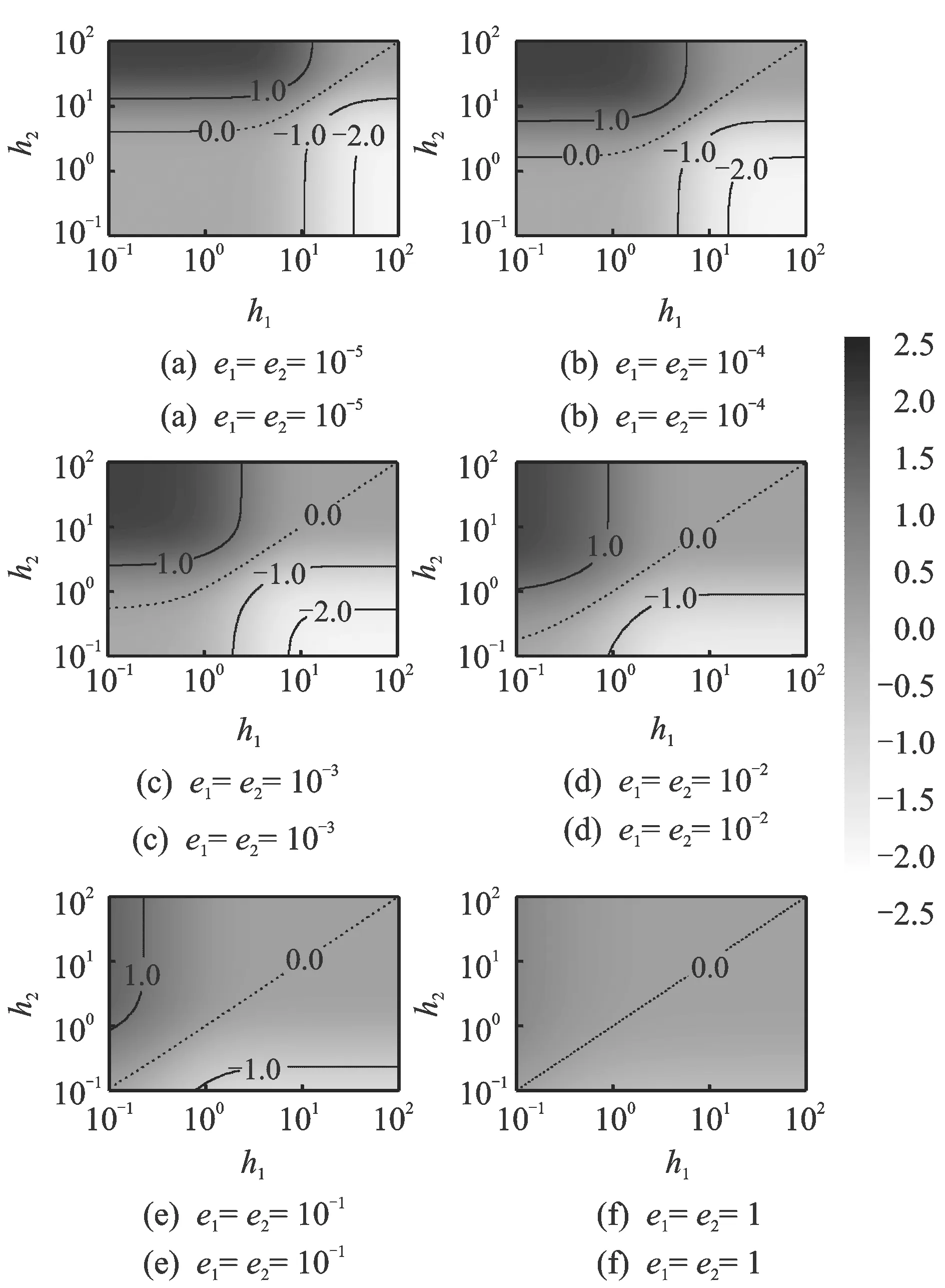
图5 比例因子lgλ和误差放大因子lgC4Fig.5 The scaling factor lgλ and error amplification factor lgC4

当图5显示为绝对误差限ε(ηs2)前的误差放大因子lgC4时，黑色区域表示误差放大因子C4远大于1，白色区域表示误差放大因子C4远小于1(对黑白区域的描述下文相同)。黑色区域是尽量要避免的区域，在黑色区域内，由于测试误差被远远放大，会导致换算结果ηs1不准确。

图6给出了绝对误差限ε(β)的误差放大因子lgC1的值。从图6可以看出，当弹性模量较小，h1<1，h2>1时，误差放大因子C1较大，随着阻尼层弹性模量的增大，C1趋于接近1。

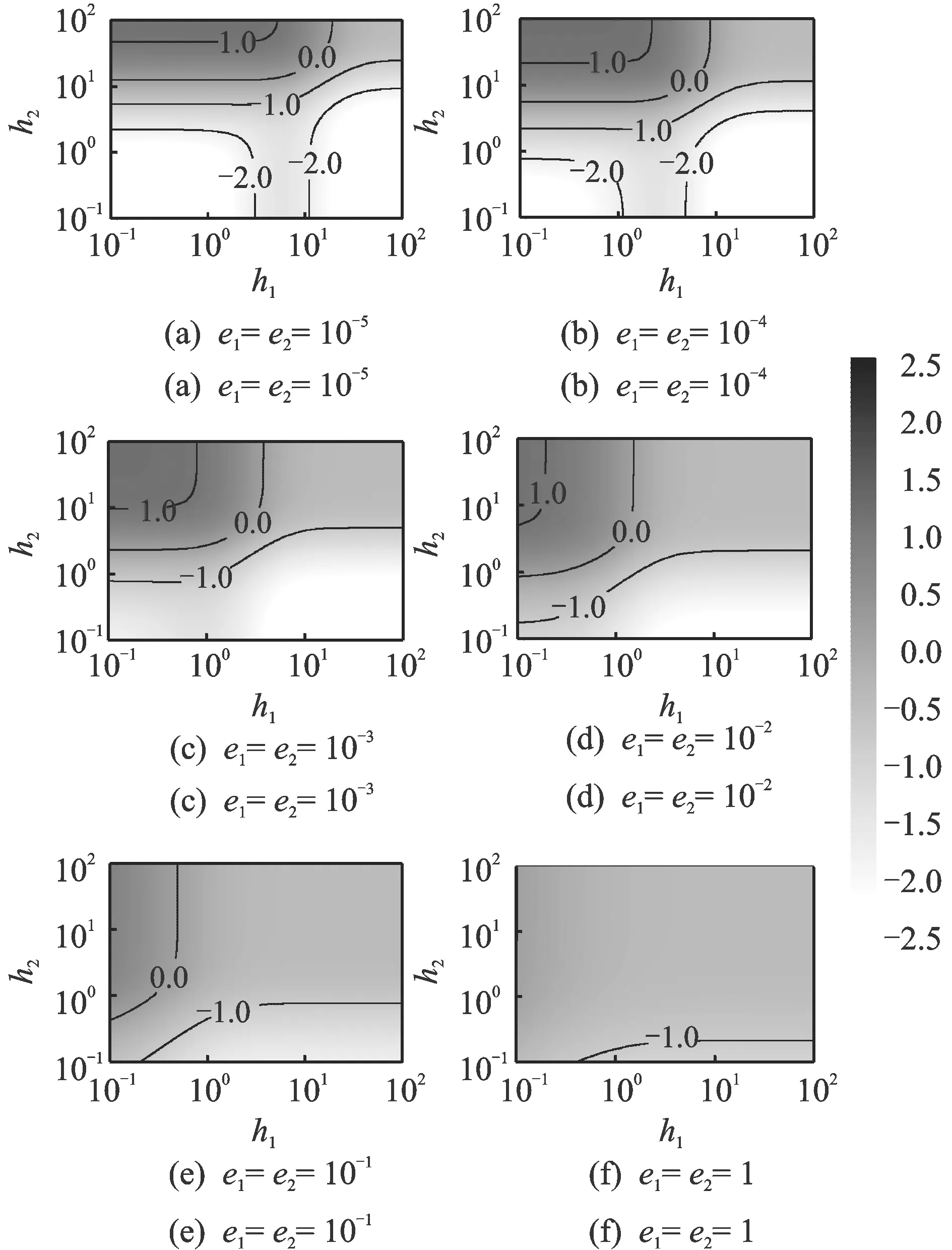
图6 绝对误差限ε(β)的误差放大因子lgC1值Fig.6 The error amplification factor lgC1 of absolute error limit ε(β)

图7给出了绝对误差限ε(α1)的误差放大因子lgC2的值，可以看出，当阻尼层弹性模量较小，误差放大因子C2较大的区域集中在云图的左下方，随着阻尼层弹性模量增大，C2逐渐减小。

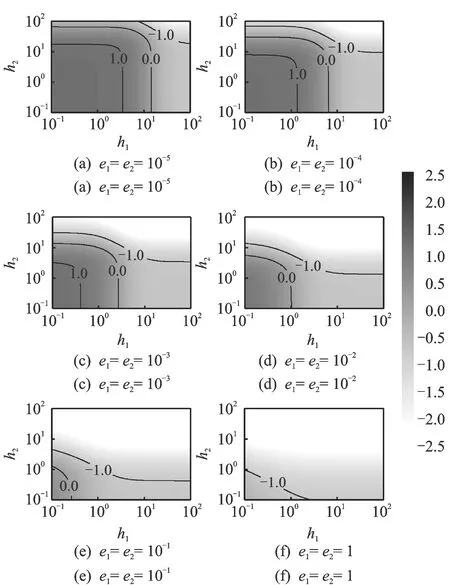
图7 绝对误差限ε(α1)的误差放大因子lgC2Fig.7 The error amplification factor lgC2of absolute error limit ε(α1)

图8给出了绝对误差限ε(α2)的误差放大因子lgC3的值。图中可以看出，C3>1的区域集中在总区域的左边。当h1<1时，误差放大因子C3值较大，随着阻尼层弹性模量的增大，误差放大因子C3>1的区域会向左边收缩。

图8 绝对误差限ε(α2)的误差放大因子lgC3Fig.8 The error amplification factor lgC3 of absolute error limit ε(α2)

比较绝对误差限ε(ηs2)，ε(β)，ε(α1)，ε(α2)前的误差放大因子可以看出，在一定的区域内，都会出现测试误差被放大的情况。综合误差放大因子的分析可以看出，提高阻尼层的弹性模量可以缩小误差放大因子大于1的区域。当阻尼层的弹性模量较小时，误差放大因子大于1的区域一般出现在云图的左上方和左下方，因此，为了避免测试误差被放大，一般建议换算基材的厚度小于目标基材的2倍且阻尼层比目标基材厚，这样，绝对误差的误差限ε(ηs2)，ε(β)，ε(α1)，ε(α2)的误差放大因子一般都小于10(或在10附近)。

借鉴前面的误差分析，经过计算可得到验证试验中ε(ηs2)，ε(β)，ε(α1)，ε(α2)前的误差放大因子分别为1.5，0.008 6～0.034 4，1.7～6.7， 2.4～9.7，均在10以内，这说明试验中各个损耗参数的测试误差没有明显地被放大，从而保证了换算过程的有效性。图4中换算值与测试值一致性良好，从侧面验证了误差分析的正确性。

综上所述，在实际工程中，一般建议阻尼层与基材的弹性模量比要大于10-5，换算基材厚度小于目标基材厚度的2倍，阻尼层比目标基材厚，以避免测试误差被远远放大。

4 结 论

1) 建立了同一阻尼层不同基材下结构损耗因子的换算关系，换算值与测试值一致性很好，验证了换算方法的正确性。

2) 对于不能直接测量的大型自由阻尼圆柱壳结构，可以通过换算得到其损耗参数的换算值，为自由阻尼圆柱壳结构敷设阻尼层的抑振效果预估提供参考方案。

3) 由于换算过程中的误差放大因子随阻尼材料的弹性模量减小而增加，为保证测量结果的精度，换算方法适合于弹性模量较大的阻尼材料，不适合于弹性模量特别小、特别薄的阻尼材料。为减少误差放大，一般建议阻尼层与基材的弹性模量比要大于10-5，换算基材厚度小于目标基材厚度的2倍，阻尼层比目标基材厚，以避免测试误差被远远放大。

[1] 胡卫强, 王敏庆, 刘志宏, 等. 阻尼材动态力学参数自动测试系统的设计[J]. 振动、测试与诊断, 2008, 28(4): 347-349.

Hu Weiqiang, Wang Minqing, Liu Zhihong, et al. An automatic test system for damping material's DMP test by swept sine half power bandwidth method[J]. Journal of Vibration,Measurement & Diagnosis, 2008, 28(4): 347-349.(in Chinese)

[2] 张教超, 王敏庆, 马建刚. 结构阻尼测声衰减时间测量方法[J]. 振动、测试与诊断, 2013, 33(2): 330-333.

Zhang Jiaochao, Wang Minqing, Ma Jiangang. Approach for determining structural damping by measurement of sound attenuation time[J]. Journal of Vibration, Measurement & Diagnosis, 2013, 33(2): 330-333.(in Chinese)

[3] Wu Lie, Agren A, Sundback U. A study of the initial decay rate of two-dimensional vibrating structures in relation to estimates of loss factor[J]. Journal of Sound and Vibration, 1997, 206(5): 663-684.

[4] Denys J M. The measurement of the loss factors of beams and plates with constrained and unconstrained damping layers: a critical assessment[J]. Journal of Sound and Vibration, 2007, 300: 744-762.

[5] Moita J S, Araújo A L, Soares C M M， et al. Finite element model for damping optimization of viscoelastic sandwich structures[J]. Advances in Engineering Software, 2013, 66: 34-39.

[6] Lu Jing, Xiang Yu, Huang Yuying, et al,. Transfer matrix method for analyzing vibration and damping characteristics of rotational shell with passive constrained layer damping treatment[J]. Acta Mechanica Solida Sinica, 2010, 23(4): 297-311.

[7] 赵志高，黄其柏.结构小阻尼测量的频域内幅值跟踪方法研究[J]. 华中科技大学学报, 2001, 29(6): 71-73.

Zhao Zhigao, Huang Qibai. An approach of light damping structure measurement by amplitude tracking in frequency domain[J]. Journal of Huazhong University of Science and Technology， 2001, 29(6): 71-73.(in Chinese)

[8] 宁方华, 张建.损耗因子测量的Hilbert变换法[J]. 山东工程学院学报, 2002, 16(1): 17-20.

Ning Fanghua, Zhang Jian. Hilbert transform in loss factor measurement[J]. Journal of Shandong Institute of Technolgy, 2002, 16(1): 17-20.(in Chinese)

[9] 阿·斯·尼基福罗夫. 船体结构声学设计[M]. 北京: 国防工业出版社, 1998:16-19.

[10]戴德沛. 阻尼减振降噪技术[M]. 西安：西安交通大学出版社, 1988:88-100.

[11]肖和业, 盛美萍, 陈永辉. 阻尼材料动态参数测量的波数方法[J]. 振动、测试与诊断, 2012,32(4): 665-669.

Xiao Heye, Sheng Meiping, Chen Yonghui. Wave number method for Young's modulus and loss factor measurement of damping material[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(4): 665-669.(in Chinese)

[12]朱蓓丽, 沈庆元.粘弹性材料复剪切模量的测量及误差分析[J]. 噪声与振动控制, 1999, 12:38-41.

Zhu Peili, Sheng Qingyuan. Measurement and error analysis of damping material's complex shear modulus[J]. Noise and Vibration Control, 1999, 12: 38-41.(in Chinese)

10.16450/j.cnki.issn.1004-6801.2015.03.029

2013-11-30；

2014-03-21

TB535.1

张安付，男，1986年8月生，博士研究生。主要研究方向为噪声与振动控制。曾发表《简支梁有效导纳仿真》(《振动、测试与诊断》2012年第32卷第5期)等论文。

E-mail:anfu1769@163.com