双树复小波包和ICA用于滚动轴承复合故障诊断*

胥永刚, 孟志鹏, 陆 明

(北京工业大学北京市精密测控技术与仪器工程技术研究中心 北京， 100124)

双树复小波包和ICA用于滚动轴承复合故障诊断*

胥永刚, 孟志鹏, 陆 明

(北京工业大学北京市精密测控技术与仪器工程技术研究中心 北京， 100124)

针对滚动轴承复合故障信号特征难以分离的问题，提出将双树复小波包变换和独立分量分析(independent component analysis，简称ICA)结合的方法应用到滚动轴承复合故障诊断中。首先，利用双树复小波包变换将复杂的、非平稳的复合故障信号分解为若干不同频带的分量；其次，引入ICA对各个分量所组成的混合信号进行盲源分离，从而尽可能消除频率混叠；最后，对从混合信号中分离出来的独立信号分量进行希尔伯特解调，即可实现对复合故障特征信息的分离和故障识别。试验结果表明，该方法可以有效地分离和提取轴承复合故障的特征频率，验证了方法的可行性和有效性。

双树复小波包变换； 独立分量分析； 盲源分离； 频率混叠； 复合故障

引 言

滚动轴承作为旋转机械最关键的零部件之一，其运行状态直接影响到整台机器的精度、可靠性及寿命等。滚动轴承故障是导致机械设备运行过程中产生故障的主要原因之一,对滚动轴承故障诊断技术进行研究具有十分重要的意义。目前，滚动轴承故障诊断方法大多只对单一故障进行了相关研究，而在实际工程应用中，故障往往不是单独出现的，而是同时发生几种故障形成复合故障。当机械设备出现复合故障时，针对非平稳的并且故障源数未知的混合信号，有效地从混合信号中分离出单一故障信号对于准确判断轴承故障十分重要。

双树复小波变换(dual-tree complex wavelet transform,简称 DTCWT)[1-2]是近几年发展起来的一种具有诸多优良特性的新型小波变换方法，具有近似平移不变性、良好的方向选择性、完全重构性、有限的数据冗余性和高效的计算效率等优良性质。但是双树复小波变换同传统小波变换一样，对高频部分没有继续进行细分。故提出双树复小波包变换[3]，对双树复小波变换中没有细分的高频部分作进一步的分解，从而提高信号整个频段的频率分辨率，减少信息的丢失。目前，双树复小波包变换在图像处理[4]、语音处理[5]和故障诊断[6-7]等领域已有相关应用。

独立分量分析(ICA)是盲源分离的一种特殊方法[8-9],其处理的对象是相互统计独立的信号源经线性组合而产生的一组混合信号,最终目的是从混合信号中分离出各自独立的信号分量。ICA在机械故障诊断、通信技术、生物医学等领域都有广泛的运用[8-11]。

双树复小波包变换相对传统离散小波包变换，频率混叠现象得到明显的抑制，但是仍然存在微小的频率混叠。笔者提出了基于双树复小波包变换和ICA的故障诊断方法，利用ICA消除双树复小波包变换的频率混叠问题，并将其应用于滚动轴承复合故障诊断中。试验结果表明，该方法可以有效地分离和提取滚动轴承复合故障的特征频率。

1 双树复小波包变换

双树复小波变换具有诸多优良的特性，但是同传统离散小波变换一样，对高频部分没有进行进一步细分。

传统的离散小波包变换(discrete wavelet packet transform ,简称DWPT)在分解时，由于每次分解都采用下抽样操作，这样使每次分解后信号的采样频率降低一半，时间分辨率也降低一半。所以一旦分解层数确定，频带的频率分辨率也就确定，分解的层数越多，频率分辨率越高，但是时间分辨率越低。同时，下抽样的操作不具有平移不变性，还会引起较大的频率混叠问题。此外，对信号的奇异点敏感，难以有效地提取信号的特征频率[7]。

针对传统小波包变换的缺陷和双树复小波变换的优良特性和不足之处，提出双树复小波包变换(dual-tree complex wavelet packet transform, 简称DT-CWPT)[3]。

双树复小波包变换的分解和重构实现非常简单，它由两个平行且使用不同的低通和高通滤波器的离散小波包变换构成，其两层分解和重构过程如图1所示。两个并行离散小波包变换，一个离散小波包变换可以看做实树，另一个小波包变换看做虚树，在信号的分解过程中可以形成互补，也能获得近似平移不变性。对双树复小波分解没有细分的高频部分也进行了分解，减少了信息的丢失。其中第1层分解，经过first_1滤波器组的为实树小波包分解。first_1滤波器有两行，第1行f1-0为低通滤波器，第1行f1-1为高通滤波器。经过first_2滤波器组的是虚部小波包分解。对于第2层以上的分解，为了保证两树在该层和所有前层上产生的延迟差的总和相对于原信号输入为一个采样周期，即两树对应滤波器的相频响应之间应有半个采样周期的群延迟, 且两滤波器的幅频响应相等，实树小波包分解交替使用Q_shift滤波器组h，同样虚部树分解交替使用Q_shift滤波器组g。在各层分解过程中采用了系数二分去除了多余的计算，提高了信号处理效率。双树复小波包变换的重构过程为分解的逆过程[3,6-7]。

图1 双树复小波包变换的分解和重构过程Fig.1 Decomposition and reconstruction process using dual-tree complex wavelet packet transform

同传统的离散小波包变换一样，由于在分解过程中隔点采样导致采样频率减半，而高频部分不满足采样定理而发生频率折叠，对高频部分继续分解就会产生频带交错。双树复小波包变换利用两树的信息互补，在一定程度抑制了频率混叠的程度，但还是存在微小的频率混叠的问题。

2 独立分量分析

独立分量分析的实质是在统计独立性的假设下，对多路观测信号进行盲分离，挖掘出隐含在观测信号中的独立源成分。

设N个观测信号X=[x1,x2,…,xN]T是由M个独立的信号源S=[s1,s2,…,sM]T的线性混合

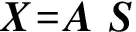
(1)

其中：A为N×M的未知混合矩阵。

盲源分离通过从观测信号中恢复出源信号矢量，即要找到一个分离矩阵W从混合信号中分离出相互独立的源信号，即

(2)

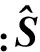
1) 对混合信号去除均值并白化处理；

2) 随机选择具有单位方差的初始分离矩阵W；

5) 如果分离矩阵收敛, 则迭代逼近过程结束, 否则返回步骤3。

得到分离矩阵W后，很容易求出源信号的估计

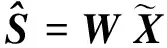
(3)

3 仿真分析

本方法的算法流程如图2所示。首先，利用DT-CWPT将原始信号分解为不同频带的分量；然后，由于分解后的分量存在一定的频率混叠，故将分解后不同分量和原始信号作为混合信号利用FastICA进行盲源分离得到各个独立的信号分量；最后，利用希尔伯特包络解调，即可有效地分离故障特征频率。

图2 基于DT-CWPT和ICA的诊断方法
Fig.2 The diagnosis method based on DT-CWPT and ICA

为了揭示双树复小波包变换在抑制频率混叠方面较传统离散小波包变换的优越性，构造如下信号

(4)

其中：x1(t)=sin(110πt)；x2(t)=sin(260πt)；

x3(t)=sin(580πt)；x4(t)=sin(640πt)。

该仿真信号的采样频率为800 Hz,采样点数为512点，分别进行2层分解。图3为传统离散小波包分解(db3小波)的波形及频谱，可以看出频率混叠较为严重，同时出现了70，270 Hz等虚假频率。图4为双树复小波包分解的波形及频谱，与图3相比较，频率混叠现象得到明显抑制，但仍然存在一定的频率混叠问题。

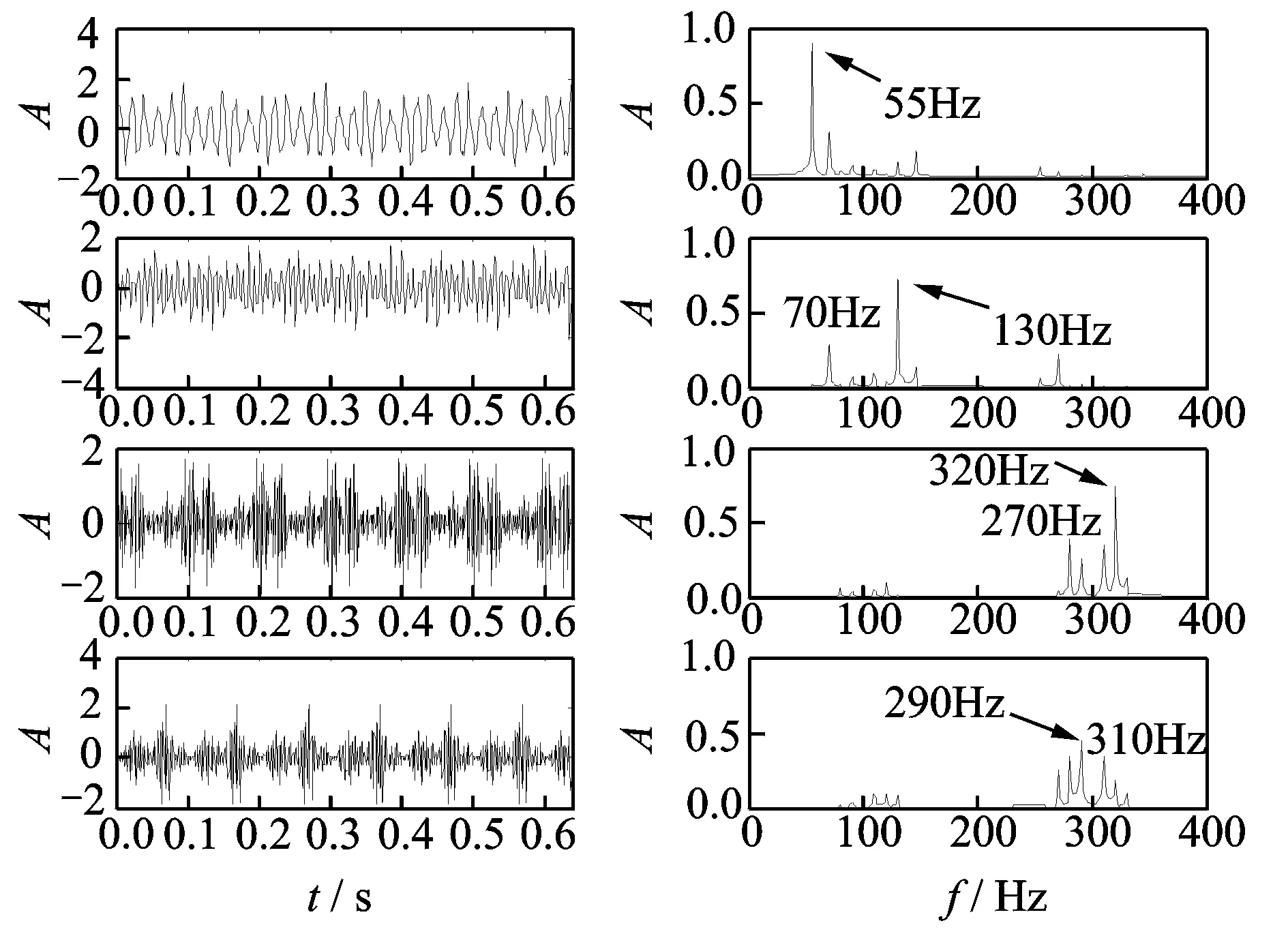
图3 2层传统离散小波包分解后的波形及频谱Fig.3 Waveforms and spectrums of 2 level CWPT decomposition

将双树复小波包分解后的4个分量和原始信号作为混合信号，利用FastICA进行盲源分离，得到的独立分量的波形及其频谱如图5所示。从盲源分离后的各个独立分量的波形和频谱图中可以看出，波形的周期性和光滑性更为理想，频率成分更为独立，已基本消除了频率混叠的现象。

图4 2层双树复小波包分解后的波形及频谱Fig.4 Waveforms and spectrums of 2 level DT-CWPT decomposition

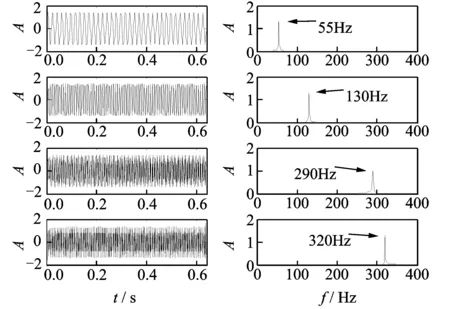
图5 FastICA 处理后波形及频谱Fig.5 Waveforms and spectrums of ICA

4 试验分析

滚动轴承故障模拟试验系统如图6所示，试验系统由轴承试验台、压电式加速度传感器、数据采集仪、笔记本电脑组成。将正常和有故障轴承依次安装在轴承试验台上，进行试验数据的采集，数据采集仪将采集数据传到电脑中，进行数据处理分析。

图6 滚动轴承故障模拟试验系统Fig.6 Bearing fault simulate experiment system

该试验的滚动轴承型号为6307，电机转速为1 496r/min，采样频率为15 360 Hz，模拟了试验台末端轴承外圈裂纹和内圈裂纹的复合故障，以及轴承外圈裂纹和滚动体点蚀的复合故障试验。其中，内外圈裂纹故障是利用线切割技术分别在轴承内圈和外圈加工了一条宽为0.5 mm、深为0.5 mm的槽来模拟。滚动体点蚀故障是采用电火花加工技术在轴承滚动体上加工了1个直径2 mm、深0.1 mm的小凹坑来模拟。

在滚动轴承运行过程中，一旦轴承部件出现裂纹、点蚀等缺陷，会产生冲击性振动，其振动频率即为轴承各部件的特征频率。在滚动轴承故障诊断过程中，利用信号处理方法检测出轴承零部件的特征频率，即可判断该零部件已产生故障。

经查询机械手册，6307轴承的滚动体直径d=13.64 mm，轴承节径D=57.5 mm，滚动体个数z=8，接触角α=0°，同时轴承内圈旋转频率fr=1 496/60=24.933 Hz，则外圈的特征为

(5)

内圈的特征频率为

(6)

滚动体的特征频率为

(7)

图7为滚动轴承同时存在内圈裂纹和外圈裂纹复合故障的原始时域波形及幅值谱，从波形和幅值谱中基本看不出故障特征信息，同时有明显的干扰成分。利用DT-CWPT对原始信号进行3层分解，得到8个频带分量a31～a38的波形如图8所示。

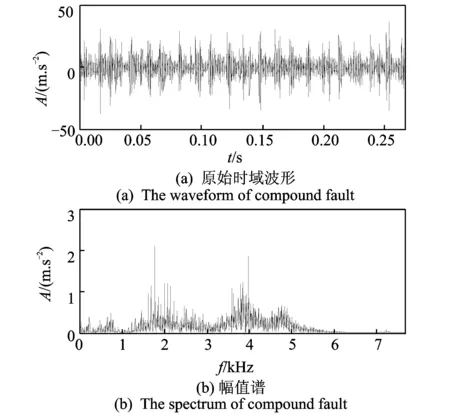
图7 内外圈裂纹复合故障波形和频谱Fig.7 Waveform and spectrum of inner and outer crack compound fault

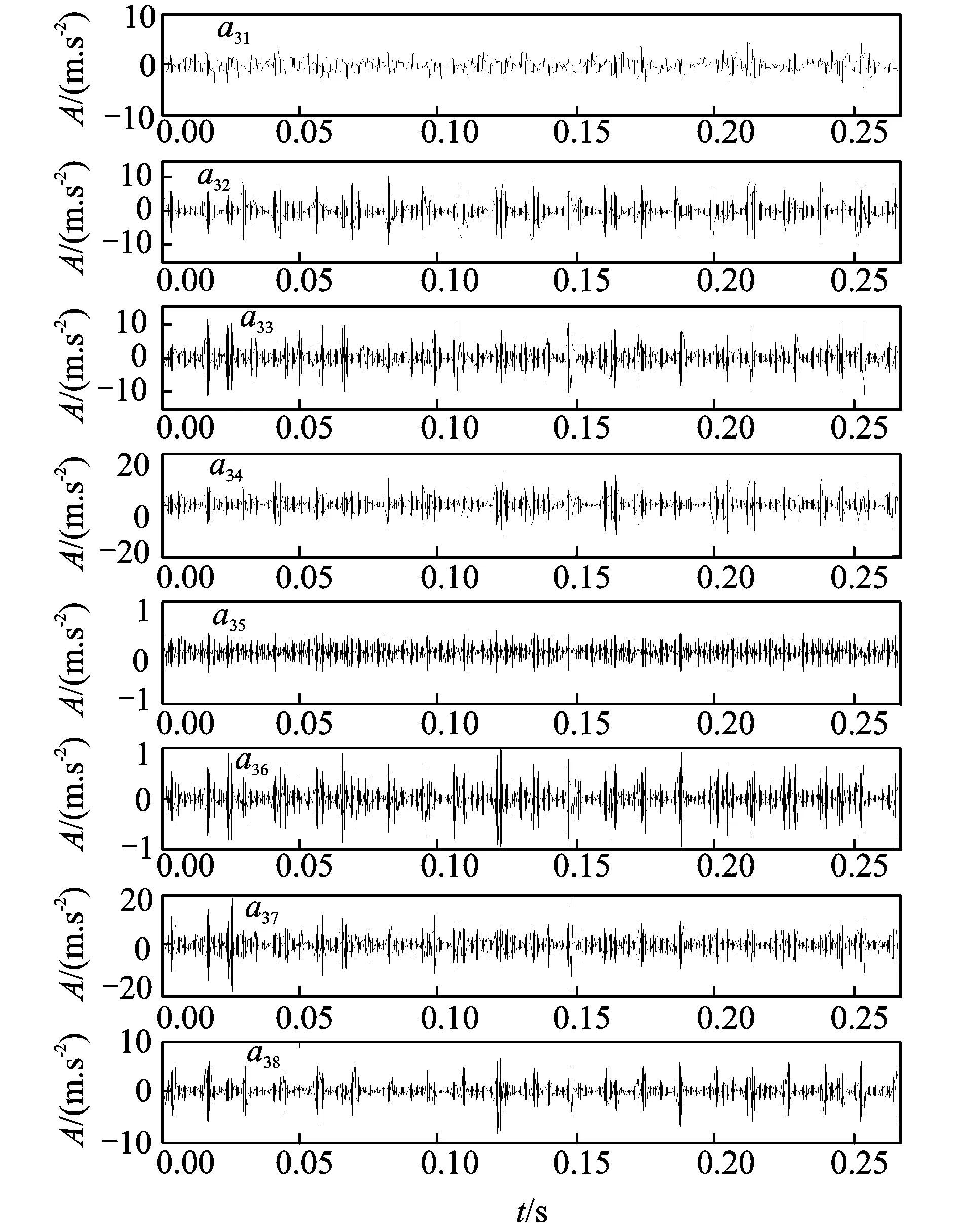
图8 双树复小波包分解结果Fig.8 Waveforms of DT-CWPT decomposition

将双树复小波包分解后的分量a32，a33，a34，a36，a37，a38以及原始信号作为混合信号(a31，a35明显为干扰成分，故去除)，利用FastICA进行盲源分离去除频率混叠得到各个独立的分量。图9所示为包含故障特征的两个独立分量的波形及其对应的希尔伯特包络解调谱。由图(b)中可以清楚地看到123.8，243.8，367.5 Hz的频率成分，与轴承内圈的特征频率122.738 Hz及其倍频非常接近，故可判断该轴承内圈存在故障。同样由图(d)中可以清楚地看到75，153.8，228.8 Hz…等频率成分，与轴承外圈的特征频率76.728 Hz及其倍频非常接近，故可判断该轴承外圈存在故障。

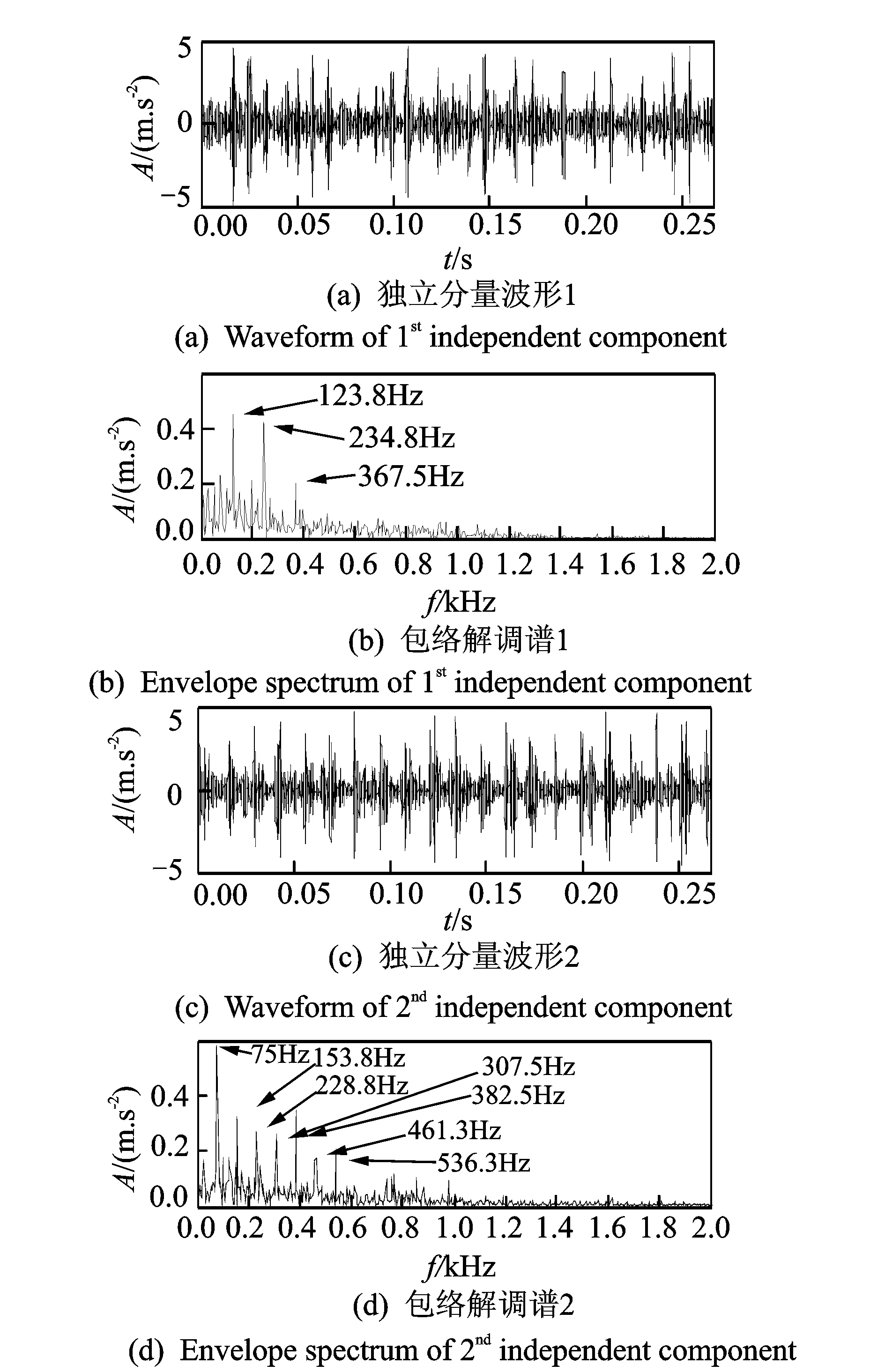
图9 内外圈复合故障FastICA分离后的波形及包络解调谱Fig.9 Waveform and envelope spectrums of inner and outer compound fault after FastICA

图10为轴承外圈裂纹和滚动体点蚀复合故障的信号时域波形和频谱。同样利用本方法进行分析，得到处理后的结果如图11所示。由图(b)中可以清楚地看到75 Hz的频率成分，与轴承外圈的特征频率76.728 Hz非常接近，故可判断该轴承外圈存在故障。同样由图(d)中可以清楚地看到52.5和105 Hz的频率成分，与轴承滚动体的特征频率51.171 Hz及其二倍频非常接近，故可判断该轴承滚动体存在故障，这与试验模拟外圈裂纹和滚动体点蚀复合故障事实相符。上述结果表明，本研究方法可以有效地分离和提取滚动轴承复合故障的特征信息。

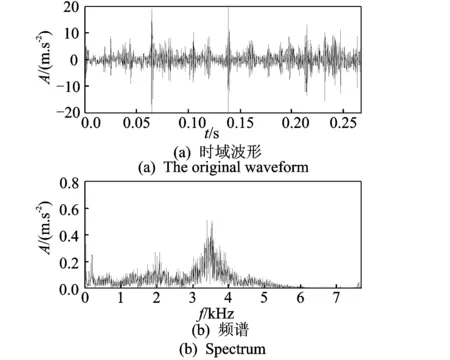
图10 外圈裂纹和滚动体点蚀复合故障波形和频谱Fig.10 Waveform and spectrum of outer crack and rolling element pitting compound fault

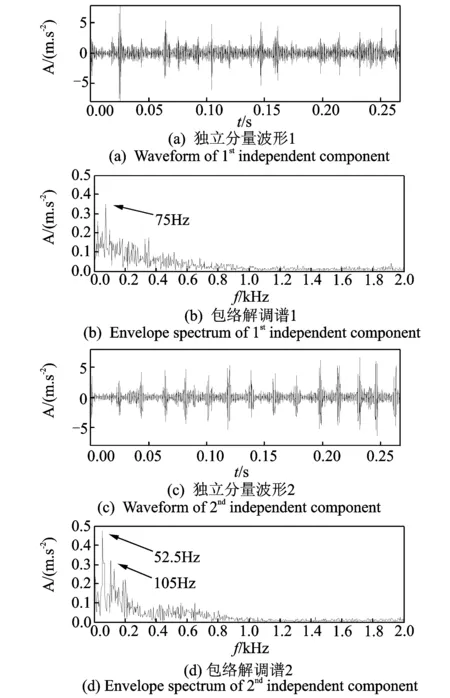
图11 外圈滚动体复合故障FastICA分离后的波形及包络解调谱Fig.11 Waveform and envelope spectrums of outer and rolling element compound fault after FastICA

5 结 论

1) 利用双树复小波包变换具有近似平移不变性、较小的频率混叠和有效降噪的优点，对复合故障信号进行分解，得到不同频段的分量，对比传统离散小波变换，双树复小波包分解效果更为理想。

2) 利用ICA对双树复小波包分解后的分量可以去除频率混叠。

3) 将双树复小波包变换与ICA结合的方法应用于复合故障诊断中，可以有效地的分离故障特征信息。

[1] Kingsbury N G. The dual-tree complex wavelet transform: a new technique for shift invariance and directional filters[J]. IEEE Digital Signal Processing Workshop,1998,98(1):2-5．

[2] Selesnick I W, Baraniuk R G, Kingsbury N G. The dual-tree complex wavelet transform[J]. IEEE Digital Signal Processing Magazine, 2005, 22(6): 123-151.

[3] Bayram I, Ivan W S. On the dual-tree complex wavelet packet and M-band transforms[J]. IEEE Transactions on Signal Processing, 2008, 56(6): 2298-2310.

[4] 翟振兴. 基于小波变换的信号去噪研究[D]. 重庆：重庆大学，2010.

[5] 王娜,郑德忠,刘永红.双树复小波包变换语音增强新算法[J].传感技术学报，2009,22(7):983-987.

Wang Na, Zheng Dezhong, Liu Yonghong. New method for speech enhancement based on dual tree complex wavelet packet transform[J]. Journal of Sensors and Actuators, 2009,22(7):983-987.(in Chinese)

[6] 吴定海,张培林,任国全，等.基于双树复小波包的发动机振动信号特征提取研究[J].振动与冲击,2010,29(4):160-164.

Wu Dinghai, Zhang Peilin, Ren Guoquan, et al. Feature extraction of an engine vibration signal based on dual tree wavelet package transformation[J]. Journal of Vibration and Shock, 2010, 29(4): 160-164. (in Chinese)

[7] 吴定海,张培林,张英堂，等.基于时频奇异谱和RVM的柴油机故障诊断研究[J].机械强度,2011,33(3):317-323.

Wu Dinghai, Zhang Peilin, Zhang Yingtang, et al. Study on diesel engine faults diagnosis based on time frequency singular value spectrum and RVM[J]. Journal of Mechanical Strength, 2011,33(3):317-323. (in Chinese)

[8] 胥永刚,张发启,何正嘉.独立分量分析及其在故障诊断中的应用[J].振动与冲击,2004,23(2):104-108.

Xu Yonggang, Zhang Faqi, He Zhengjia. Independent component analysis and its application to fault diagnosis [J].Journal of Vibration and Shock, 2004, 23(2):104-108. (in Chinese)

[9] 周晓峰, 杨世锡, 甘春标.一种旋转机械振动信号的盲源分离消噪方法[J].振动、测试与诊断,2012,32(5):714-717.

Zhou Xiaofeng, Yang Shixi, Gan Chunbiao. De-noising vibration signal of rotating machinery with blind sources separation[J]. Journal of Vibration, Measurement & Diagnosis, 2012,32(5):714-717. (in Chinese)

[10]艾延廷,费成巍,张凤玲,等.ICA在航空发动机振动信号盲源分离中的应用[J].振动、测试与诊断,2010,30(6):671-674.

Ai Yanting, Fei Chengwei, Zhang Fengling, et al. Blind source separation for aero-engines vibration signal by independent component analysis[J]. Journal of Vibration, Measurement & Diagnosis, 2010,30(6):671-674. (in Chinese)

[11]Hyvbrinen A, Oja E. Independent component analysis[J]. Neural Computing Surveys, 1999, 2: 94-128.

10.16450/j.cnki.issn.1004-6801.2015.03.018

*国家自然科学基金资助项目(51075009)；北京市优秀人才培养资助计划项目(2011D005015000006)

2013-02-24；

2013-04-09

TH133.3； TH165

胥永刚，男，1975年10月生，博士、副教授。主要研究方向为机械故障诊断、现代信号处理等。曾发表《双树复小波和奇异差分谱在滚动轴承故障诊断中的应用》(《振动工程学报》2013年第26卷第6期)等论文。 E-mail: xyg@bjut.edu.cn