一类偶数阶中立型泛函偏微分系统的振动准则*

罗李平，罗振国，杨 柳

(衡阳师范学院统计学院，湖南 衡阳 421002)



一类偶数阶中立型泛函偏微分系统的振动准则*

罗李平，罗振国，杨 柳

(衡阳师范学院统计学院，湖南 衡阳 421002)

考虑一类具连续滞量和非线性扩散项的偶数阶中立型泛函偏微分系统，利用一种基于一类核函数Φ(t,s,r)和Riccati变换的新技巧，建立了该类系统在Robin边值条件下所有解振动的若干新的充分条件。

振动性；泛函偏微分系统；偶数阶；中立型；核函数

在自然科学和工程技术研究中，许多现象都用(偏)微分系统作为其数学模型，但都是假定事物的变化规律只与当时状态有关，而与过去历史状态无关。但在实际问题中，一个系统将来的行为不仅依赖于现在的状态，也受过去状态的影响。因此，用传统的(偏)微分系统去描述系统状态只是一种近似，并不能精确描述，取而代之的是带有各种滞后量(特别是带时间滞后量)的(偏)微分系统，被统称为泛函(偏)微分系统。由于泛函(偏)微分系统充分考虑到历史因素(即滞后量)对系统的影响，故能更精确地描述实际现象，在物理学、生物数学、经济数学、自动控制、通讯理论等学科领域中都广泛地涉及到它。振动性理论作为泛函偏微分系统定性理论的重要分支之一，对其展开研究具有重要的理论价值和实用价值。近年来，关于泛函偏微分系统的振动性研究已取得了一些很好的结果[1-7]，但关于具连续滞量和非线性扩散项的泛函偏微分系统(尤其是高阶情形)的振动性的研究还不多见。本文的目的是着手研究如下的具连续滞量和非线性扩散项的偶数阶中立型泛函偏微分系统

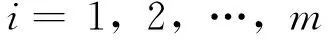
(E)

在Robin边值条件

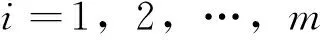
(B)

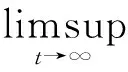
本文中，如不特别说明，总假设下列条件成立：

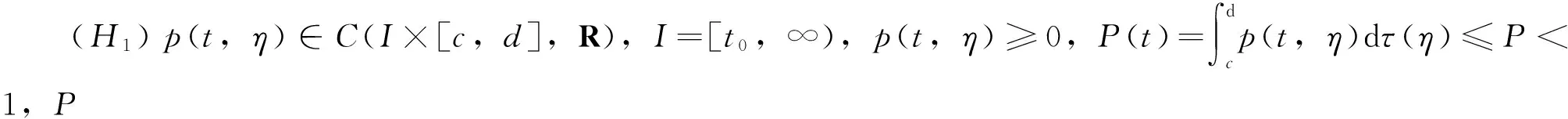
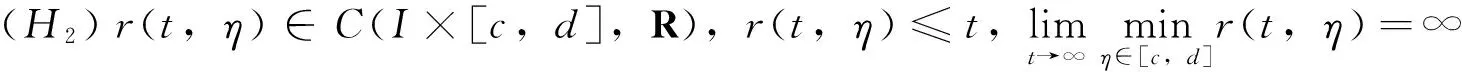
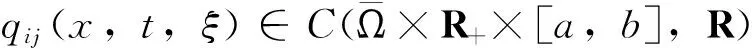
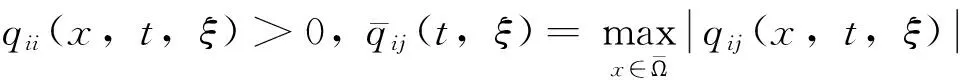
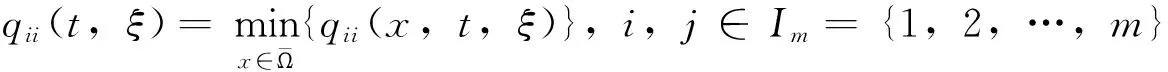
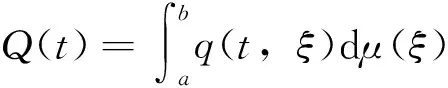
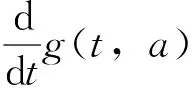
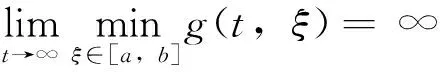
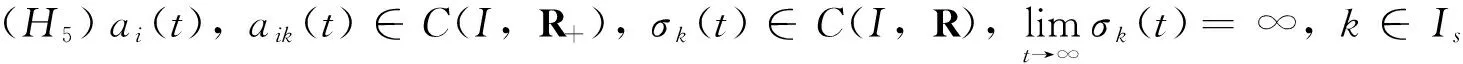
(H6)hi(ui),hik(ui)∈C1(R,R+)，

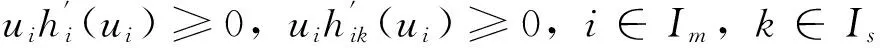
(H7)τ(η),μ(ξ)分别为[c,d]和[a,b]上非减函数。

1 定义及引理

定义1 称向量函数

为边值问题(E)、(B)的解，若它在G内满足方程组(E)且在∂Ω×R+上满足边界条件(B)。

定义2 称数值函数v(x,t)在G内振动，若对任意正数β，存在点(x0,t0)∈Ω×[β,∞)，使得v(x0,t0)=0，否则，称为非振动的；称边值问题(E)、(B)的解u(x,t)在G内振动，若它至少有一个分量作为数值函数是振动的；称边值问题(E)、(B)的解u(x,t)在G内非振动，若它的每一个分量作为数值函数都是非振动的。

定义3 设D={(t,s):t≥s≥t0}，称函数H=H(t,s)属于函数类X，记作H∈X，若H∈C(D,R)满足：当t≥t0时，H(t,t)=0；当t>s≥t0时，H(t,s)>0，并且在D上关于t和s有连续偏导数。

定义4 设E={(t,s,r):t≥s≥r≥t0},称函数Φ=Φ(t,s,r)属于函数类Y，记作Φ∈Y，若Φ∈C(E,R)满足：当t≥r≥t0时，Φ(t,t,r)=Φ(t,r,r)=0；当t>s>r≥t0时，Φ(t,s,r)>0，并且在E上关于s有连续偏导数。

设Φ∈Y，g(t)∈C([t0,R),R)，定义算子T[*;r,t]如下

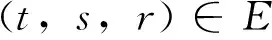
(1)

函数φ(t,s,r)定义为

(2)

注1 容易验证算子T[*;r,t]是线性算子，并且满足

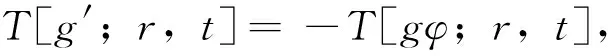
(3)

注2 易知对任意H1,H2∈X，有H1(t,s)H2(s,r)∈Y。

引理1[8]设y(t)∈Cn(I,R)为常号，在I上y(n)(t)≠0且满足y(n)(t)y(t)≤0，则

(i) 存在t1≥t0，使得y(i)(t)(i=1,2,…,n-1)在[t1,∞)上常号；

(ii) 存在l∈{0,1,2,…,n-1},n+l为奇数，使得

y(i)(t)>0,t≥t1,i=0,1,2,…,l；

(-1)i+ly(i)(t)>0,t≥t1,i=l+1,…,n

引理2[9]设y(t)满足引理1的条件，且y(n-1)(t)y(n)(t)≤0,t≥t1，则对每一θ∈(0,1)，存在常数N>0，使得

2 主要结果及其证明

定理1 若微分不等式

(4)

无最终正解，其中λ=1-P，N是某一正数，则边值问题(E)、(B)的所有解在G内振动。

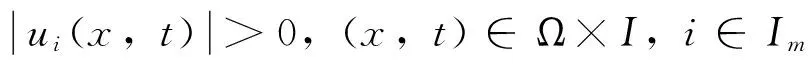
问题(E)两边关于x在Ω上积分，有

(5)

交换积分顺序有

(6)

利用Green公式，边界条件(B)及(H6)，得到

(7)

(8)

其中dS是∂Ω上的面积元素。

联合式(5)-式(8)，并注意到条件(H3)，(H5)，有

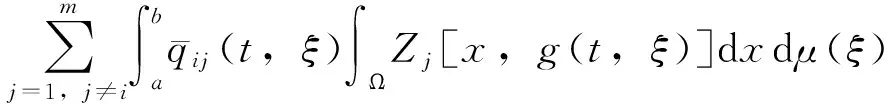
t≥t1，i∈Im

(9)

令Vi(t)=∫ΩZi(x,t)dx，t≥t1，i∈Im，显然Vi(t)>0，t≥t1，i∈Im，于是由式(9)有

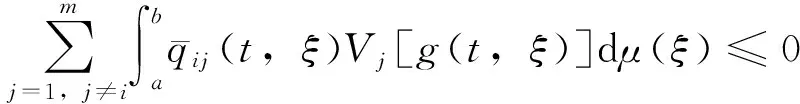
t≥t1，i∈Im

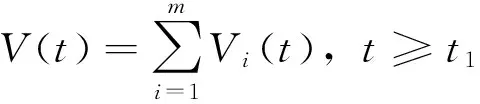
t≥t1

(10)

注意到

于是由式(10)有

(11)

令

(12)

则z(t)≥V(t)>0，并且结合式(11)有

t≥t1

(13)

于是由引理1知，存在t2≥t1，使得z′(t)>0和z(n-1)(t)>0，t≥t2。由式(12)有

(14)

联合式(13)和式(14)产生

(15)

令

(16)

则W(t)>0，t≥t2。因z(t)是增函数，g(t,ξ)关于t和ξ非减，故存在t3≥t2，使得

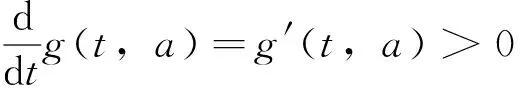
(17)

于是由式(15)- 式(17)有

即

(18)

此示W(t)是微分不等式(4)的一个最终正解，而这与定理1的题设矛盾。证毕。

定理2 若对任意r≥t0，存在函数Φ∈Y，使得

(19)

其中算子T和函数φ(t,s,r)分别由式(1)和式(2)定义，则边值问题(E)、(B)的所有解在G内振动。

证明 由定理1知，只需要证明在定理2的条件下，微分不等式(4)无最终正解即可。

假设微分不等式(4)存在一个解W(t)在[t0,∞)(t0>0)上无零点，不失一般性，不妨设W(t)>0，t∈[t1,∞)，t1≥t0。由不等式(4)有

t≥t1

(20)

对式(20)应用算子T[*;r,t](t≥r≥t1)，并利用式(3)可得

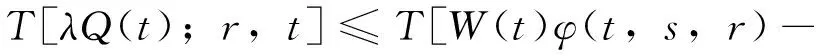
于是对任意t≥r≥t1，有

(21)

对式(21)取上极限，可得

此与式(19)相矛盾。证毕。

注3 由定理1可知，选择不同的核函数Φ(t,s,r)，通过简单的计算，可得到边值问题(E)、(B)不同的振动准则。

若取Φ(t,s,r)=H1(t,s)H2(s,r)，其中H1,H2∈X。由定理1可得如下定理。

定理3 若对任意r≥t0，存在函数H1,H2∈X，使得

其中h1,h2定义如下

(22)

h1,h2在D上局部可积，则边值问题(E)、(B)的所有解在G内振动。

若取Φ(t,s,r)=ρ(s)(t-s)α(s-r)β，其中ρ(s)∈C1(I,R+)，α,β>1为常数。由定理1可得如下定理。

定理4 若对任意r≥t0，存在函数ρ(s)∈C1(I,R+)和常数α,β>1，使得

则边值问题(E)、(B)的所有解在G内振动。

注4 我们可以看到，定理2-定理4中的结果都包含系数p和qij的积分，因此需要系数在整个区间I上的信息。然而根据Stum分离定理，振动性仅仅是一个区间性质。因此，下面对边值问题(E)、 (B)的区间振动性质做进一步的研究，建立了几个新的区间振动准则，这些准则仅仅是基于系数在I的一系列子区间上的信息。

定理5 若对任意r≥t0，存在函数Φ∈Y和常数v>u≥r，使得

其中算子T和函数φ(v,s,u)分别由式(1)和式(2)定义，则边值问题(E)、(B)的所有解在G内振动。

证明 同定理2的证明，将其中的t,r分别用v和u替换，容易看到微分不等式(4)的每一个解在区间(u,v)中至少有一个零点，即不等式(4)的每一个解在I上有任意大的零点，因此微分不等式(4)无最终正解。由定理1知，边值问题(E)、(B)的所有解在G内振动。证毕。

类似于注3的讨论，可得如下结果。

定理6 若对任意r≥t0，存在函数H1,H2∈X和常数v>u≥r，使得

其中h1,h2由式(22)定义，则边值问题(E)、(B)的所有解在G内振动。

定理7 若对任意r≥t0，存在函数ρ(s)∈C1(I,R+)和常数α,β>1，v>u≥r，使得

则边值问题(E)、(B)的所有解在G内振动。

[1]LIYK.Oscillationsofsystemsofhyperbolicdifferentialequationswithdeviatingarguments[J].ActaMathSinica, 1997, 40(1): 100-105.

[2]GUANXP,YANGJ.Oscillationofsystemsofnonlinearhyperbolicpartialfunctionaldifferentialequationsofneutraltype[J].JSysSci&MathScis, 1998, 18(2): 239-246.

[3]LIWN,CUIBT.Oscillationforsystemsofneutraldelayhyperbolicdifferentialequations[J].IndianJPureApplMath, 2000, 31: 933-948.

[4]DENGLH,GEWG,YUYH.Oscillationofsystemsofquasilinearparabolicfunctionaldifferentialequationsaboutboundaryvalueproblems[J].ActaMathApplSinica, 2001, 24(2): 295-301.

[5]LIWN,CUIBT,DEBNATHL.Oscillationofsystemsofcertainneutraldelayparabolicdifferentialequations[J].JApplMathStochasticAnal, 2003, 16(1): 83-94.

[6]WANGPG,WUYH.Oscillationofsolutionsforsystemsofhyperbolicequationsofneutraltype[J].ElectronicJournalofDifferentialEquations, 2004, 2004(80):1-8.

[7]DENGLH,MUCL.Oscillationofsolutionsofthesystemsofquasilinearhyperbolicequationsundernonlinearboundarycondition[J].ActaMathScientia, 2007, 27B(3): 656-662.

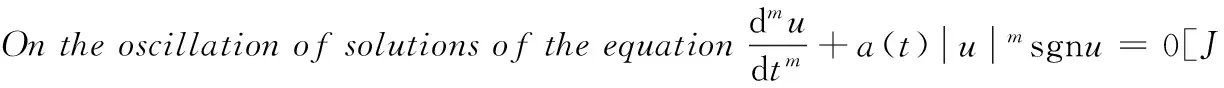
[9]PHILOSCG.Anewcriterionforoscillatoryandasymptoticbehaviorofdelaydifferentialequations[J].BullAcadPolSciSerSciMat, 1981, 29: 367-370.

Oscillation Criteria of Certain Even Order Neutral Functional Partial Differential Systems

LUOLiping,LUOZhenguo,YANGLiu

(College of Mathematics and Statistics, Hengyang Normal University, Hengyang 421002, China)

A class of even order neutral functional partial differential systems with continuous delay and nonlinear diffusion term is studied. By using a new technique based on a class of kernel functionsΦ(t,s,r)andRiccati’stransformation,somenewsufficientconditionsforoscillationofallsolutionsofsuchsystemsareestablishedunderRobin’sboundaryvaluecondition.

oscillation; functional partial differential system; even order; neutral type; kernel function

10.13471/j.cnki.acta.snus.2015.06.010

2015-04-08 基金项目：湖南省“十二五”重点建设学科资助项目(湘教发[2011]76)；湖南省自然科学基金青年资助项目(13JJ4098)

罗李平(1964年生)，男；研究方向：(脉冲)偏微分方程解的性态;E-mail:luolp3456034@163.com

O

A

0529-6579(2015)06-0050-05