太阳帆板驱动机构微振动建模及摩擦补偿研究
张可墨,张 强,程俊波
(北京控制工程研究所,北京 100190)
太阳帆板驱动机构微振动建模及摩擦补偿研究
张可墨,张 强,程俊波
(北京控制工程研究所,北京 100190)
从太阳帆板驱动机构(SADA)微振动产生机理出发,考虑电机谐波力矩和导电环摩擦力矩对电机输出力矩的影响,建立以永磁同步电机(PMSM)为驱动源的闭环SADA模型及其与挠性负载耦合的动力学方程.通过拟合电机低速运行时导电环摩擦力矩随转速的变化曲线,利用非线性最小二乘法辨识摩擦模型静态参数,并在电机闭环反馈调节机制中引入摩擦补偿环节.通过对比和分析摩擦补偿前后电机控制量以及帆板转速输出的变化,仿真结果表明摩擦补偿在一定程度上消除了摩擦对SADA低速运行性能的影响,为降低SADA对超静卫星平台和高性能载荷的影响以及展开对其微振动优化和抑制提供依据.
SADA;微振动;永磁同步电机;Striebeck摩擦;摩擦补偿.
0 引 言
目前太阳能是航天器最主要的能量来源.随着航天技术的发展和航天任务的复杂化,卫星多附有大型太阳电池阵结构,又称太阳帆板.卫星在轨运行期间,太阳帆板驱动机构(SADA,solar array drive assembly)一方面驱动太阳电池阵作相对转动,使其法线与太阳光射束重合以获取尽可能多的太阳能[1],另一方面将太阳能转化成电能输送到航天器本体中[2],为卫星在轨工作提供主要的电源.
作为航天器微振动源之一的太阳帆板驱动机构,正常运行过程中会产生频率丰富的扰动力和力矩,持续激发航天器结构振动与姿态抖动.随着中国高性能航天器的发展,搭载的有效载荷精度越来越高,同时也对卫星平台微振动提出了越来越严苛的要求.SADA微振动不仅会对有效载荷核心性能的实现产生不利影响,例如降低对地观测卫星的成像质量,增加激光通信卫星的误码率和导致空间科学实验无法开展等.特别是当太阳帆板为挠性结构时,SADA微振动可能会使帆板受激励,直接影响卫星姿态控制的精度和稳定度,严重时导致太阳帆板停转[3].
国外研究机构对SADA微振动机理[4-5]、建模[6-8]的研究全面深入,已形成较完备的试验数据库并成功应用于工程实践.国内研究多以步进电机作为驱动源,数学模型简单、试验数据零散.由于步进电机受脉冲控制,驱动过程中复杂的扰动力矩会导致帆板转速波动较大.印度ISRO公司则花了大量精力研究高性能低谐波力矩步进电机[9],以改善驱动平稳性.哈勃空间望远镜的两台SADA,采用直流无刷电机直接驱动方案,但还未有公开文献报道该SADA的详细指标和具体方案.考虑SADA驱动太阳帆板对整星姿态控制的扰动是高精、高稳卫星平台研制和应用的重要环节,很多SADA研制机构转而采用永磁同步电机(PMSM,permanent magnet synchronous motor)直接驱动并结合闭环反馈的技术方案,以实现负载的平滑驱动.
本文在研究SADA微振动产生机理的基础上,建立以PMSM为驱动源,SADA闭环驱动帆板的动力学模型.分析低速运行条件下Striebeck摩擦对电机输出力矩的影响,利用非线性最小二乘法辨识摩擦模型的静态参数,并在电机闭环反馈调节机制中引入摩擦补偿环节.通过仿真,验证SADA微振动模型的正确性,对比摩擦补偿前后电机控制量及帆板转速输出的变化,分析导电环摩擦对电机运行的影响.结果表明,摩擦补偿在一定程度上消除了摩擦对SADA低速运行性能的不良影响,为降低SADA对超静卫星平台和高性能载荷的影响提供了依据.
1 SADA微振动问题描述
SADA主要包括线路和机构两个部分,其中机构是SADA微振动的主要来源,包括驱动电机、从电机到输出轴的传动装置及其轴承、功率导电环、信号导电环、输出轴角位置传感器和机构结构本体等,如图1所示.

图1 闭环SADA对日定向示意图Fig.1 Diagram of a closed-loop SADA driven by PMSM
产生SADA微振动的两个重要因素是电机电磁力矩和机构摩擦力矩,这可由SADA驱动太阳帆板的动力学方程明显看出.式(1)给出了太阳帆板为刚性时最简单的动力学方程:
(1)
其中,J为太阳帆板沿驱动轴的转动惯量,Jm为电机转子的转动惯量,且Jm≪J,Ω为帆板转速,τe为电机电磁力矩,τf为机构摩擦力矩.通过以往经验结合试验发现,轴承组件摩擦力矩数值比导电环组件小1到3个数量级,因此认为机构中导电环摩擦是τf的主要来源.
1.1 永磁同步电机
太阳帆板驱动机构的核心部件是电机,采用正弦波永磁同步电机作为SADA驱动电机,以实现负载的平滑驱动.由于不含减速器组件,电机是在极低速的情况下运行的,故采用基于转子磁场定向的矢量控制(VC,vector control),以实现高性能的磁场定位控制.由于电流闭环采用直轴电流id和交轴电流iq进行反馈控制,而电枢绕组的实际电流是三相交流电流ia、ib和ic,因此必须经过3/2变换以及d-q旋转变换,得到以电流为状态变量的状态方程:
(2)
式中,ud、uq和id、iq分别表示定子侧d、q轴的电压和电流;Rs表示定子侧的电枢电阻;ω表示转子的电角速度;Ld、Lq表示定子侧d、q轴的电感;Ψr表示转子永磁体在定子绕组中产生的磁链,即转子永磁磁链.

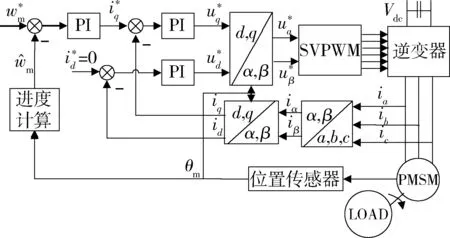
图2 基于转子磁场定向的永磁同步电机矢量控制方案Fig.2 Vector control of permanent magnet synchronous motor
1.2 导电环组件
导电环组件是SADA的重要组成部分,用于在存在相互运动的部件之间传递电信号或功率信号.电刷触点与滑环上表面发生相对运动,二者的接触摩擦会形成一定的扰振力,并通过滑环及电刷的安装结构传递至卫星安装界面.当前国内外大多数SADA研制机构都是从优化设计角度来减少摩擦,很少从模型补偿角度来消除摩擦的影响.
一般地,相互运动的接触面之间的摩擦力Ff与相对速度v间的关系可用非线性函数Ff=f(v)描述.目前工程上常用“静摩擦+库仑摩擦+粘性摩擦”[11]描述摩擦现象,如图3所示.摩擦同速度间的静态关系描述为:(1)库仑摩擦Fc,是非0速下的摩擦,只取决于速度或者角速度的符号(2)粘滞摩擦,与速度成比例,即粘性摩擦系数fv(3)静摩擦力Fs,是速度为0时的摩擦力,一般大于库仑摩擦力.

图3 库仑摩擦、粘性摩擦和静摩擦Fig.3 Coulomb friction, viscous friction and static friction
大量摩擦试验表明在有润滑的接触情况下, “静摩擦+库仑摩擦+粘性摩擦”模型不能解释太阳帆板转动速率处于临界转速附近时摩擦力矩产生的复杂扰动,即在相对滑动速度较低的范围内,随着相对速度的增加摩擦力反而下降的Striebeck效应[12].
2 SADA微振动模型
采用永磁同步电机驱动的SADA,电机转速Ωm、转角αm与帆板转速Ω、转角α的关系为αm=α,Ωm=Ω.
定子绕组电压方程为
(3)
定子绕组磁链方程为
(4)
电磁转矩方程为
τe=pn(iqψd-idψq)
=pn[ψriq+(Ld-Lq)idiq]
(5)
式中,pn表示转子极对数,Ψd、Ψq表示定子侧d、q轴的磁链,对于采用表贴式转子结构的永磁同步电机有Ld=Lq,电磁转矩可以简化为τe=pnψriq.设永磁同步电机转子永磁磁链ψr不变,即dψr/dt=0,定子绕组电压方程可以写为
(6)
假设电流采样结果能够真实地反映实际电流,则d、q两轴电压的PI调节量为
(7)

(8)

设旋变分辨率为Ks位,Ns为旋转当量,θs为旋变精度,函数[x]表示对x向0取整,n为白噪声,则旋变当前输出角度为
(9)
当前转速为
(10)
式中α-1为前一时刻输出转角,Tc为控制周期.
为抑制传感器噪声的影响,对差分转速进行FIR低通滤波
(11)
由于齿槽的存在,气隙不均匀,故气隙磁导率不是常数,由此会产生齿槽转矩.忽略电机绕组互感、外界干扰力矩和高次谐波分量,齿槽定位力矩只考虑4次谐波,设p′为定子齿槽数,则4阶齿槽力矩为
τcog=5%×pnψriqmaxsin(4p′α)
(12)
描述导电环摩擦力矩的Tustin模型为
τf=(τc+(τs-τc)e-|Ω|/Ωs)·sign(Ω)+fvΩ
(13)
式中,摩擦参数[τc,τs,Ωs,fv]由经验或实测确定.
帆板驱动力矩为
τ=τe-τcog-τf
(14)
太阳帆板运动学方程为

(15)
只考虑一阶挠性模态,挠性太阳帆板动力学方程为
(16)
式中,η、φ分别为模态坐标和模态速率,K为模态刚度,D为模态阻尼.设阻尼比为ξ,则D=2ξωf,K=ωf2,ωf为挠性模态频率.帆板刚度K及挠性耦合系数δ由帆板结构有限元分析给出.与卫星姿态动力学的接口关系为
TIs
(17)
3 摩擦补偿环节设计
3.1 摩擦模型及参数辨识
对于给定数据{(xi,yi),j=1,2,…,N},即导电环组件摩擦试验实测数据,估计参数使下列二乘误差最小[13]
(18)
式中,y=[y1,y2,…,yN]T,a=[a1,a2,…,an]T.设Vd为设计矩阵,由选用的拟合方法决定;拟合参数个数n由Vd决定.相应的拟合方程为
y=VdaT
(19)
出于数值计算稳定性考虑,对设计矩阵Vd实施QR分解,获得正交阵列Q和三角阵R后,拟合系数可由下式获得
(20)

(21)
式中,v=N-n是统计量的自由度.拟合系数的标准差sa及置信区间为
(22)
采用基于最小二乘原理的非线性方法拟合试验数据,得到导电环摩擦力矩与帆板转速之间的函数关系拟合结果,如图4所示.

图4 95%以上置信度的非线性拟合Fig.4 Nonlinear regression with 95% confidence intervals

(23)

J=1/2∑e2(α,Ωi)
(24)
极小化目标函数即可得到辨识结果,如图5所示.

图5 95%以上置信度的参数辨识Fig.5 Parameter estimation with 95% confidence intervals
3.2 摩擦补偿及电机PI控制
考虑加入一个过零点的正弦测试信号,以验证离线辨识结果的有效性及摩擦对电机控制系统的影响.从图6可以看出,电机转子转动前的摩擦力矩总是在正负最大静摩擦力矩之间跳跃,直到电机转矩大到足够克服静摩擦而进入部分液体润滑阶段,摩擦力矩才随着转速成比较好的线性关系.由于采用PI控制,转速跟踪没有出现过零点的失真.仿真结果表明,模型能够很好地反映零点附近低速运行情况下,摩擦环节对电机控制系统的影响.
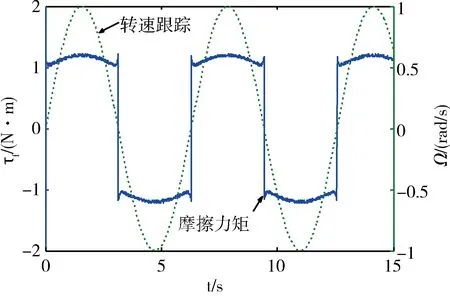
图6 正弦指令转速下的摩擦力矩Fig.6 Friction torque with sinusoid speed input
为消除摩擦力矩对电机运行的不良影响,将辨识得到的参数带入摩擦模型,将其产生的摩擦力矩估计值加入到控制力矩中.这种基于摩擦模型的补偿方法,实质是对永磁同步电机控制系统以电流的形式进行前馈补偿,将式(5)代入式(14)可得补偿电流为
(25)
式中if为基于辨识摩擦模型的前馈补偿电流.
4 仿真验证
设指令转速Ωd= 0.06(°)/s,其余参数如表1所示.

表1 仿真参数


图7 d、q两轴调节电压Fig.7 Modulating voltage of d、q axises
图9所示是摩擦力矩补偿前后转速跟踪指令变化情况,可以看出在补偿掉摩擦力矩后,帆板转速能很快响应至稳态.频谱分析显示,峰值频率不变但转速幅值降低了50%以上.

图8 d、q两轴电流Fig.8 Current of d、q axises

图9 帆板转速及转速频谱Fig.9 Solar cell array’s speed and it’s frequency spectrum
5 结 论
本文在建立闭环SADA永磁同步电机驱动帆板动力学模型的基础上,利用非线性最小二乘法辨识Striebeck摩擦模型的静态参数,在电机闭环反馈调节机制中设计并引入摩擦补偿环节.通过数学仿真,对比摩擦补偿前后电机控制量及帆板转速输出的变化,分析摩擦对低速条件下电机运行性能的影响.结果表明:摩擦补偿前,电机控制量和速度响应都出现了大的超调和振荡;摩擦补偿后,闭环SADA低速跟踪性能明显提高,在很大程度上克服了摩擦对低速运行性能的影响,也从另一方面说明摩擦补偿对抑制稳态极限环振荡有明显效果.
[1] 高星,王友平.太阳电池阵驱动机构的通用化、系列化和组合化设计[J].空间科学学报,2002,22(增刊Ⅱ):55-68. GAO X, WANG Y P. The universalization, serialization and modularization design of solar array drive assembly (SADA)[J]. Chinese Journal of Space Science, 2002,22(Ⅱ):55-68.
[2] 陈烈民. 航天器结构与机构[M].北京:中国科学技术出版社, 2005:358.
[3] 张宗美. 航天故障手册[M]. 北京:宇航出版社, 1994:171-200.
[4] CABILIC J, FOUMIER J P. Design consideration on the solar array drive mechanism developed for SPOT[C]// The 2ndSpace Tribology Workshop. Risley, UK: ESTL, 1980.
[5] ATLAS G, THOMIN G. Experiences of CNES and SEP on space mechanisms rotating at low speed[R]. Washington D.C: NASA, N87-29868, 1987.
[6] ETZLER C C. Dynamic analysis of a BAPTA-solar generator system[C]//The 1stEuropean Symposium on Space Mechanisim & Tribology, Neuchatel, Switz, 1983.
[7] ROGER F, SON N. Development of the Solar Array Deployment and Drive System for the XTE Spacecraft[R]. Washington D.C: NASA, N95-27284, 1995.
[8] MARIO C R, SEBASTIAO E C V. Development of a BAPTA mechanism for small satellites[C]//Astro-dynamics Specialist Conference. Girdwood, Alaska: AAS/AIAA, 1999.
[9] RAJAGOPAL K R, KRISHNASWAMY M,et al. An improved high resolution hybrid stepper motor for solar array drive of Indian remote sensing satellite[J]. IEEE Transactions on Industry Applications, 1997,33(4):906-913.
[10] 唐任远.现代永磁电机理论与设计[M].北京: 机械工业出版社,1997:252-264.
[11] 刘丽兰,刘宏昭,吴子英,等.机械系统中摩擦模型的研究进展[J].力学进展,2008,38(2):201-213. LIU L Y,LIU H Z,WU Z Y,et al.An overview of friction models in mechanical systems[J].Advances in Mechnics,2008,38(2): 201-213.
[12] ARMSTRONG H B. Stick slip and control in low-speed motion[J].IEEE Transactions on Automatic Control, 1993,38(10):1483-1496.
[13] 张志涌.精通Matlab R2011a[M]. 北京:北京航空航天大学出版社,2011:165-170.
Micro-Vibration Modeling of SADA and Friction Compensation for the Control of PMSM
ZHANG Kemo, ZHANG Qiang, CHENG Junbo
(BeijingInstituteofControlEngineering,Beijing100190,China)
From learning the mechanism of SADA (solar array drive assembly) micro-vibration, taking motor ripple torque and friction of slip-ring into account, a systemic model of the closed-loop SADA driven by PMSM (permanent magnet synchronous motor) is established. The coupling dynamical equation between flexible solar cell arrays and motor driver is built. The friction of slip-ring is modeled by Striebeck effect, whose parameters are identified off-line via nonlinear least square. Based on PI control strategy, the feed-forward compensation is presented with the estimated value of the identified model. The simulation results show that the model-based friction compensation can accurately estimate and compensate the friction nonlinearity with high precision and faster system response, by which the accuracy of speed tracking and performance of motor at low velocity are improved.
SADA; micro-vibration; PMSM; striebeck friction; friction compensation
2014-12-13
V414
A
1674-1579(2015)05-0033-06
10.3969/j.issn.1674-1579.2015.05.007
张可墨(1990—),女,硕士研究生,研究方向为航天器执行机构微振动特性和测试;张 强(1978—),男,高级工程师,研究方向为航天器执行机构技术;程俊波(1983—),男,博士研究生,研究方向为电机驱动与控制.

