一种基于串联解耦的陀螺飞轮摆角控制方法*
章晓明,李海军
(1.上海航天控制技术研究所,上海 200233;2.上海市空间智能控制技术重点实验室,上海 200233)
一种基于串联解耦的陀螺飞轮摆角控制方法*
章晓明1,2,李海军1,2
(1.上海航天控制技术研究所,上海 200233;2.上海市空间智能控制技术重点实验室,上海 200233)
陀螺飞轮通过挠性支撑的动量轮转子加减速及侧向摆动实现三轴控制力矩输出,飞轮转子两维侧摆伺服系统是实现三轴力矩输出功能的关键.高速转子两维侧摆运动存在强耦合,采用常规的PID控制器无法实现两通道独立输出控制力矩.给出了一种解耦控制方法,通过串联解耦矩阵实现两维摆角解耦控制,并通过实时计算解耦矩阵系数解决解耦矩阵随飞轮转子转速时变的问题.数值仿真结果验证了这种解耦控制方法的有效性.
陀螺飞轮;串联解耦;摆角控制.
0 引 言
陀螺飞轮是一种用于小卫星姿态控制的执行机构.它的结构类似于两自由度动力调谐陀螺,即用一个两自由度挠性支架支撑动量转子,挠性支架与驱动轴固连[1].驱动轴在电机拖动下高速旋转,并通过加减速在驱动轴方向上输出控制力矩.飞轮转子在一个两维力矩器作用下实现两自由度侧摆,通过改变飞轮动量矩的方向在与驱动轴垂直的平面内输出两轴控制力矩.因此陀螺飞轮是一种可以实现三轴力矩输出的执行机构.一台陀螺飞轮可以同时实现一台偏置动量飞轮和两台零动量反作用飞轮的功能,其自旋轴角动量为整星提供偏置角动量,并通过电机加减速(飞轮工作模式)以及转子有限转角侧摆运动(力矩陀螺工作模式)吸收环境干扰力矩.由于小卫星受到的干扰力矩较小,动量轮小范围内的侧摆运动即可满足小卫星对动量轮角动量吸收能力的要求.
国内外对陀螺飞轮的研究开始于20世纪90年代.1999年Tyc等[2]在第十三届美国AIAA会议上提出陀螺飞轮的构想,同时他们在会议上还宣告其样机已研制成功并阐述了其工作原理.随后Walkty等[3]对陀螺飞轮的动力学建模进行了叙述和分析.运用复数域分析法对经典控制算法(根轨迹法和频域分析法)进行改进,用于陀螺飞轮复系数模型分析,提出了陀螺飞轮系统的设计方案.该方案采用固定系数校正网络实现飞轮转子侧摆运动控制,未考虑高速飞轮转子在侧摆过程中的解耦问题及控制系统参数随飞轮转速改变而引起的变化[4].
本文在对陀螺飞轮摆角控制时变模型建模和分析基础上,提出了一种数字式串联解耦控制器设计方法,并通过数值仿真验证了这种解耦控制方法的有效性.
1 陀螺飞轮摆角控制模型
1.1 控制对象
陀螺飞轮结构如图1所示,摆角伺服系统包括挠性框架支撑的转子、两维力矩器、两维摆角传感器.挠性框架支撑的飞轮转子可实现两维侧摆,摆角范围±4°;两维摆角传感器利用变磁阻原理检测其两维摆角作为反馈信号[5];两维力矩器依据反馈控制信号对飞轮体施加控制力矩实现侧摆伺服控制.
1.2 控制对象传递函数
陀螺飞轮转子的动力学方程可写为[5]
(1)

(2)
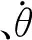
对式(1)进行拉式变换可以得到陀螺飞轮两维摆角与力矩器控制力矩及壳体角速度之间的传递函数矩阵(3).其中K、H是转子转速的函数,该系统是一个时变系统.
(3)
在系统开环条件下,转子侧摆运动表现出明显的耦合现象.图2是转子对一个通道控制力矩的开环响应特性曲线.从图示曲线可以明显看出其耦合特性及随转子转速变化的特性.

图2 陀螺飞轮摆角开环响应特性Fig.2 Swing angle characteristic under aopen-loop control
2 串联解耦控制器设计
定义
(4)
则式(3)可以写为式(5)
(5)
式(5)中与力矩器输出力矩相关的传递函数是系统的可控部分,与外界角速度相关的传递函数是系统不可控部分.可控部分的传递函数矩阵存在耦合项.为了实现两维摆角控制,希望通过一个矫正网络使该动态过程解耦,这样就可以将一个两输入、两输出的耦合系统简化为两个单输入、单输出系统,在此基础上进行综合设计.使用前馈补偿器解耦是较简单的方法,只需要在待解耦系统的前面串接一个前馈补偿器,使串联组合系统的传递函数成为对角的有理函数矩阵,即可实现系统解耦.
设解耦后的系统传递函数矩阵为N(s),前馈补偿传递函数矩阵为M(s),取
M(s)=G-1(s)N(s)
(6)
则该前馈环节与原系统串联
G(s)M(s)=G(s)G-1(s)N(s)=N(s)
(7)
即可获得所要的解耦系统.对(4)式求逆得到
(8)
并设解耦后的系统为一个Ⅱ型系统(9),这样就可以常值偏角跟踪常值角加速度输入,以零偏角跟踪常值角速度输入.
(9)
式(8)、(9)代入式(6)得到所求的解耦矩阵
(10)
解耦后系统的极点为0,是一个临界稳定系统,需要串联控制器才能保证系统稳定.控制器Gc(s)采用常规的PID矫正网络,其形式为
Mx(s)=kpβ(s)+kdsβ(s)+kiβ(s)/s,
My(s)=kpα(s)+kdsα(s)+kiα(s)/s
(11)
最终的控制器可由一个PID矫正网络加一个串联解耦网络组成,其系统框图见图3.
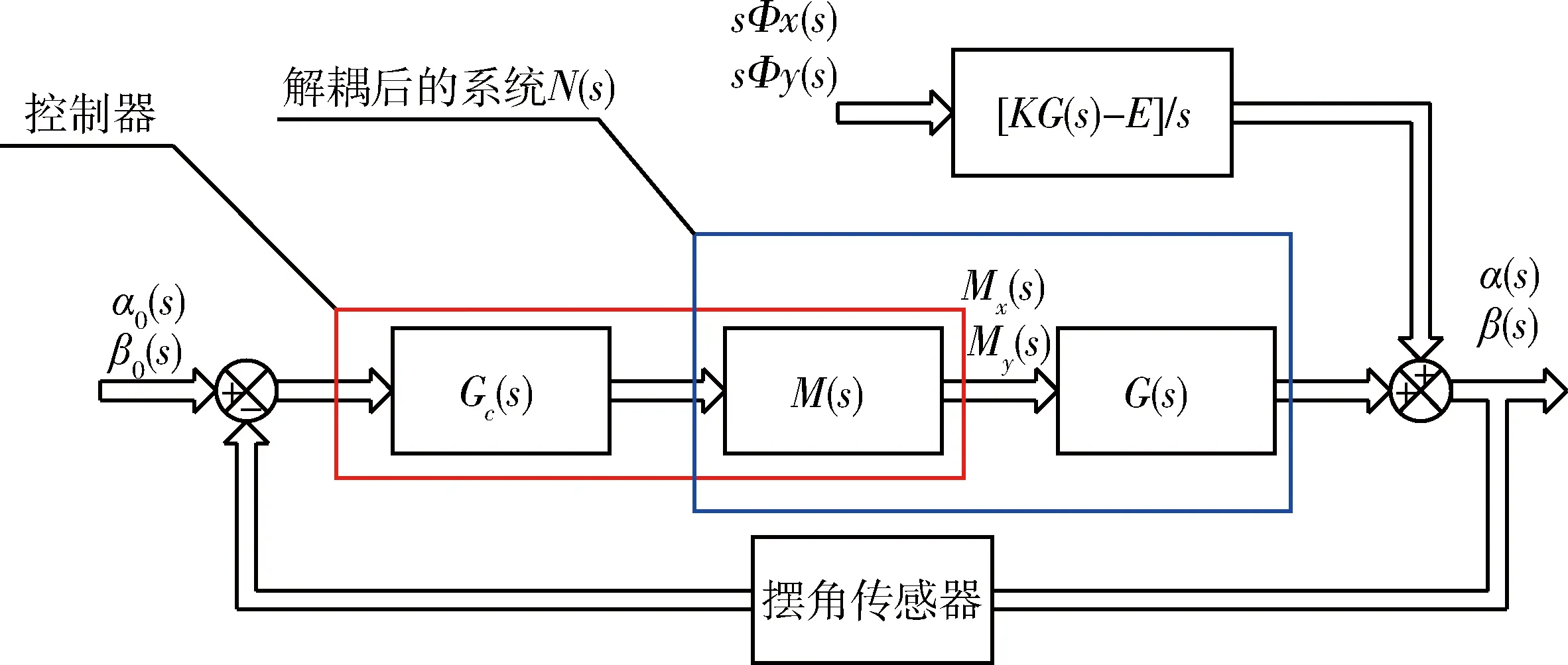
图3 串联解耦控制器框图Fig.3 Series system for decoupling control
3 系统时变性的解决方法
式(9)给出的解耦矩阵包含时变项K(剩余刚度)和H(转子角动量),它们是转子转速的函数.为了实现系统解耦,必须根据飞轮转速实测值在线更新解耦矩阵系数.这种控制方法可以用数字控制器实现,图4给出了数字控制器的执行流程图.

图4 数字控制器计算流程图Fig.4 Numeric controller flow chart
K和H的计算需要用到转子极转动惯量、赤道转动惯量、平衡环极转动惯量、赤道转动惯量.对一个实际的陀螺飞轮,这些惯量值是常量,通过CAD软件可以给出精确的设计值.通常陀螺飞轮这类精密的执行机构,其零部件经过精密加工制造而成,因此部件实际惯量值与设计值的偏差对闭环控制系统而言是可接受的.

图5 摆角解耦控制仿真曲线Fig.5 Swing angle characteristic under a close-loop control
4 解耦控制算法验证
针对某型陀螺飞轮的设计参数,采用本文设计的解耦矩阵进行数值计算验证解耦算法.计算参数为:
平衡环惯性张量
(12)
转子惯性张量
(13)
挠性框架刚度系数Kp=0.56(N·m)/rad,PID控制器采用常规的Ziegler-Nichols整定方法确定,两个通道采用同样的参数:kp=100,kd=0.1,ki=10.
图5是一组典型的仿真结果,仿真工况为飞轮转子转速从3 000 r/min加速至3 500 r/min;同时,对转子两维摆角伺服系统输入阶跃指令,使其分别在两个摆动方向上偏转4°并保持稳定.图中给出了摆角响应特性及力矩器输出力矩特性.在前1 s内,转子摆角从0°位移动到4°,此后在4°位置上保持稳定.力矩器输出力矩在前1 s内经历一个动态过程,而后保持常值,该常值力矩用于平衡挠性框架在高转速下产生的动力反弹性力矩,使转子稳定地绕倾斜轴线旋转.从图中曲线可知,采用本文设计的解耦控制算法较好地实现了高速转子两维摆角解耦控制,在时变参数条件下能够实现系统解耦及稳定控制.
5 结 论
陀螺飞轮高速转子两维摆角伺服控制系统的传递函数是一个双输入、双输出时变系统,两个通道存在较明显的耦合效应,采用常规的单通道PID控制器无法实现两维摆角独立控制.本文采用串联解耦方法设计了一种解耦网络,采用该校正网络将陀螺飞轮高速转子两维摆角的传递函数改造为两个相互独立的单输入单输出系统,串联解耦后再采用常规的PID控制器实现系统稳定控制.考虑到两维摆角控制对象的传递函数是飞轮转子自旋转速的函数,可以通过实时计算解耦矩阵系数来消除解耦矩阵随飞轮转子转速时变的问题.最后通过一组典型工况下的数值仿真结论验证了解耦控制方法的可行性.
[1] TYC G, STALEY DA,虎刚.陀螺飞轮——一种用于航天器三轴姿态控制的新型执行机构/敏感器[J].控制工程,2001(3):32-40.
[2] TYC G, STALEY D A, WHITEHEAD W R, et al. Gyrowheel-an gyrowheel an innovative new actuator/sensor for 3 axis spacecraft attitude control[C]//Proceedings of the 13thAnnual AIAA/USU Conference on Small Satellites.Washington D.C.:AIAA,1999:1-13.
[3] WALKTY I, PETERSEN J, DOHERTY T, et al. SCISAT-1 ACE mission C&DH unit development[C]//Proceeding of 14thAnnual/USU Conference on Small Satellites.2000:1-13.
[4] HARRISON P T.Development and testing of a GyroWheel based control system for the SCISAT-1 scientific satellite[M].[S.l.]:[s.n.],2004.
[5] 刘希珠,雷田玉.陀螺力学基础[M].北京:清华大学出版社.1987:200-201
A Control Method of Gyrowheel’s Swing Angle Based on Series Decoupling
ZHANG Xiaoming1,2, LI Haijun1,2
(1.ShanghaiInstituteofSpaceflightControlTechnology,Shanghai200233,China;2.ShanghaiKeyLaboratoryofSpaceIntelligentControlTechnology,Shanghai200233,China)
A gryowheel can output torques in three directions via changing the angular momentum’s amplitude or direction. The servo system for swing angle control is the key to achieving the function of triaxial torque output. There is a strong coupling between the high-speed rotor’s swings in two directions so that the output torques in two directions independently is unavailable under normal PID control methods. A method for decoupling control is provided via adding a series of system matrices and creating two decoupling systems. The coefficients of the series of system matrices are changing as rotor speed changing. It can be solved by calculating the coefficients in a real time digital control processor. Numerical simulation result shows the feasibility of this control method.
gyrowheel; series decoupling; swing angle control
*国防科工局民用航天预先研究课题资助项目.
2015-03-12
V448
A
1674-1579(2015)05-0023-05
10.3969/j.issn.1674-1579.2015.05.005
章晓明(1983—), 工程师,专业:机械设计制造及其自动化,研究方向:空间执行机构研究;李海军(1980—),高级工程师,专业:导航,制导与控制,研究方向:飞行器控制与导航.

