串并混联空间机械臂全自由度轨迹规划算法*
王 勇,唐 强,徐拴锋,朱志斌,何英姿,魏春岭
(1.北京控制工程研究所,北京 100190; 2.空间智能控制技术重点实验室,北京 100190)
串并混联空间机械臂全自由度轨迹规划算法*
王 勇1,2,唐 强1,2,徐拴锋1,2,朱志斌1,2,何英姿1,2,魏春岭1,2
(1.北京控制工程研究所,北京 100190; 2.空间智能控制技术重点实验室,北京 100190)
目前,国内外对串并混联空间机械臂的研究较少;而且大多在舍弃冗余自由度的情况下进行轨迹规划.针对7自由度串并混联空间机械臂,提出了一种基于解析解、并且充分放开全部7个自由度的机械臂轨迹规划算法.该规划算法既扩大了串并混联空间机械臂的规划可达空间,又保证了规划的实时性,同时还保留了结构承载能力强的优点,可以充分发挥其作为空间抓捕用臂的优势.通过仿真和地面空间操作抓捕试验,验证了算法的有效性.
空间机器人;空间操作;轨迹规划;串并混联;冗余自由度.
0 引 言
近年来,以美欧俄日为代表的航天大国正在大力发展空间操作控制技术,并开展了相关的在轨飞行演示验证[1-4].因此,大力推进空间操作关键技术攻关非常重要,这将有助于中国在空间维护和操作领域中占据优势地位.
与地面固定基座机器人不同,空间机器人处于失重环境下,且由于任务需要,空间机械连杆多为细长,材料也多选用轻质材料.对于传统的串联机械臂,其工作空间大、结构灵巧,但承载能力不足.串联构型的空间机械臂在运行过程中,难免会给机器人系统引入较大振动,机械臂的颤动或变形可能会导致目标抓取失败、设备损坏等问题.并联机械臂承载能力强、结构紧凑,但其缺点是工作空间小.串并混联机械臂则兼顾上述两种机械臂的优点[5].将一部串联机械臂安装于另一部并联机械臂上,这种结构不仅具有较高的刚度,而且末端定位精度也有较大提升[6-7].
在对目标进行近距离操作时,考虑到安全性和节省燃料等要求,空间机械臂的基座通常是自由漂浮的[8].无论是否对基座进行控制,由于参数不确定性和各种干扰等因素,在抓捕过程中,基座的实际位姿与期望位姿相比均会具有一定的偏差[9],这就对空间机械臂的性能,尤其是其运动范围提出了较高要求.即使采用了串并混联的结构设计,并联机构部分也会对机械臂系统的运动空间带来一定的影响,若不针对其运动范围进行改进,较大的基座停靠位姿偏差可能就会在客观上直接导致机械臂无法对目标完成抓捕.通常来讲,机械臂一旦设计完成,其可运动范围就由轨迹规划及控制算法来决定了.常见的机械臂轨迹规划大都是针对时间或能量最优进行设计的[10-11],这种算法计算复杂度高、也很少特别针对可运动范围进行优化.
为此,本文设计了一条7自由度串并混联空间机械臂原理样机,其具有一个冗余自由度.同时,为了扩大机械臂的工作空间,提出了一种基于解析解、并且充分利用全部7个自由度的机械臂轨迹规划算法.进而,通过仿真以及在6自由度气浮台上进行的空间抓捕试验,对算法的有效性进行了分析和验证.
1 串并混联机械臂的逆运动学解算
1.1 串并混联机械臂的模型及坐标系定义
人类的手臂由肩部、上臂、前臂、手腕、手等部分组成,其中,在进行运动时,通常是肩部受力最大,这与机械臂在进行抓捕等操作时一致,为了适应这种力的分配情况,设计了一种新型的7自由度串并混联机械臂,并将其作为空间抓捕机械臂的原型样机,如图1所示.机械臂由下臂、上臂两部分组成,具有7个自由度.其中,下臂采用3支链并联形式,具有3个自由度,其中主支链为UP形式,2根辅支链为UPS形式(U表示虎克铰,P表示移动副,S表示球铰);上臂采用4自由度串联形式.

图1 7自由度串并混联机械臂Fig.1 7 DOFs series-parallel manipulator
图1中可以看到,UP支链的两个转动轴与肘部的方位转动轴交于一点,因此,该构型的机械臂具有解析形式的反解结果.解析解一个很大的优势就是使机械臂的控制和规划(如力控制等)可以充分满足实时性的需求.由于机构具有7个自由度,当给定末端位姿,理论上各关节的输入值具有无数个解,因此,求解时必须固定其中一个自由度.考虑到控制实时性要求,将并联部分UP支链伸长量给定,并联臂此时仅具有2个转动自由度(可视为绕UP支链虎克铰的两个转动),此时机械臂等效为一个6自由度的串联机械臂.等效的机械臂模型及坐标系定义如图2所示.
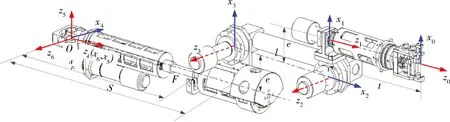
图2 机械臂模型及坐标系定义Fig.2 Model and reference frame definition of manipulator
1.2 串并混联机械臂的逆运动学解算
与运动学解算过程相反,当机器人末端工具坐标系与目标位姿矩阵重合时,求各关节转角θi的过程称为逆运动学解算,下面将简要叙述求取过程.首先,根据图2列出DH参数[12],如表1所示.其中,表中各变量含义已在图2中进行标注.
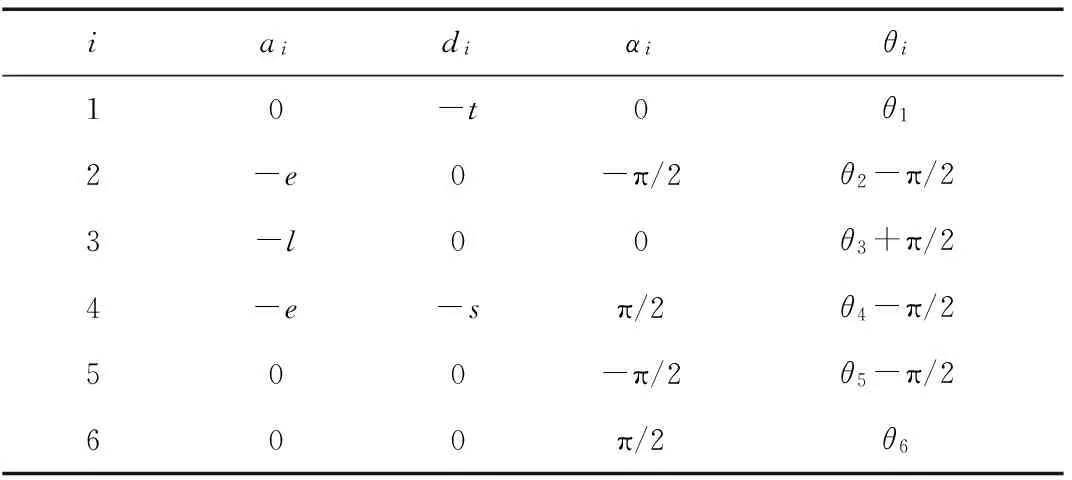
表1 机械臂模型的DH参数
(1)
(1)求解θ3
令

定义:
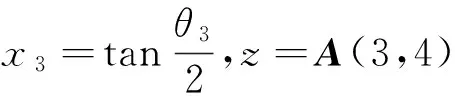
r=A(1,4)2+A(2,4)2+A(3,4)2
其中,A(i,j)表示A矩阵的第i行、第j列元素.借助于坐标系4、5、6的原点汇于一点这一特点,可以得到关于x3的一元四次方程,形式如下:
(2)
其中,
C4θ3= 4e2l2-4e2r+4e2z2-4el3+4elr-4els2+
l4-2l2r+2l2s2+r2-2rs2+s4,
C3θ3=8l3s-16el2s+8ls3-8rls,
C2θ3=-8e2l2-8e2r+8e2z2+2l4-4l2r+
20l2s2+2r2-4rs2+2s4,
C1θ3=8l3s+16el2s+8ls3-8rls,
C0θ3=4e2l2-4e2r+4e2z2+4el3-4elr+4els2+
l4-2l2r+2l2s2+r2-2rs2+s4.
利用牛顿迭代法,即可实现x3的求取,进而可以得到θ3=2arctan(x3).
(2)求解θ2
(3)
其中,

C2θ2= -2e2-l2+2le-2e2m+2esn+
2elm-s2-2lsn,
C1θ2=4sme+4e2n,
C0θ2=r-2e2-l2-2le+2e2m-2esn+
2elm-s2-2lsn.
通过式(3)可以解出x2,求得的多根需要再代入式(4)中进行验证:
(4)
其中,
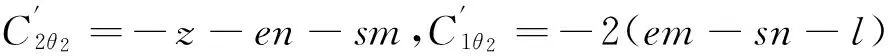

(3)求解θ1

(5)
其中,

C2θ1=qsm+qen-e+pl-pem+psn+p4x,
C1θ1=0,
C0θ1=p4x-qsm-qen+e-pl+pem-psn.
p4x为4、5、6三个坐标系相交的原点在机械臂基坐标系下的x坐标,可由DH参数直接计算得到.
通过式(5)可以解出x1,求得的多根需要再代入下式进行验证
(6)
其中,


选取满足要求的解,可以解出θ1=2arctan(x1).
(4)求解θ4、θ5、θ6
令
(7)


θ5=-arccos(-Tp(2,3)),θ5≠kπ(k为整数),
(8)
其中,Tp(i,j)表示Tp矩阵的第i行、第j列元素.
在1.1节中已经提到,解算时UP支链伸长量是给定的,θ6和θ5是为了求解虚拟出来的转角,因此,还需要给出UPS支链对应的长度.图3是并联部分的模型及坐标系定义.

图3 机械臂并联结构模型及坐标系Fig.3 Model and reference frame definition of manipulator parallel structure
根据几何关系很容易得到UPS支链长度
(9)
(10)
2 全自由度轨迹规划算法
2.1 固定的UP支链对机械臂可达空间的影响
为了得到唯一的解析解,在求解过程中,固定了UP支链的长度.根据图3中并联结构模型示意图可知,机械臂并联部分的可达空间由2个虚拟的转角θ6和θ5反映.这两个转角不仅会随着UPS支链的变化而变化,UP支链的变化对也会对其造成影响.图4为θ6和θ5随着UP支链长度s的变化而变化情况.

图4 虚拟转角受UP支链长度的影响Fig.4 Influence on virtual DOFs from UP-chain length
可以看到,当UP支链长度s取不同数值时,机械臂的运动范围是不同的.在传统的轨迹规划算法中,UP支链长度s往往是固定的,这样带来的问题就是,无法控制机械臂到达能力所及的极限范围.为此,本文提出了一种基于解析解、并充分放开UP支链长度的轨迹规划算法.
2.2 轨迹规划算法
通过上面的分析可以知道,在规划机械臂的运动轨迹时,为了尽可能的扩大其运动范围,需要在规划过程中将冗余的自由度s放开.一旦放开s以后,从理论上看,机械臂末端的可达空间将扩大为不同s情况下机械臂可达空间的合集.此时,虽然机械臂末端的可达空间增大了,但若在规划时让末端按照固定轨迹,如直线连续运动,可以发现,由于运动过程中无法穿越奇异区域,机械臂的连续运动空间依然不会很大,而若采用复杂的轨迹规划又会给实际运行带来不必要的困难.因此,在机械臂轨迹规划过程中,将规划做在了关节空间上,而不是笛卡尔空间上.基于上述思路,本文提出的机械臂轨迹规划算法流程如图5所示.

图5 全自由度轨迹规划算法Fig.5 Trajectory-planning algorithm based on the full DOFs
利用逆运动学解析公式得到目标机器人构型之后,与当前机器人构型做差值等分,计算得到的步长即可作为机械臂各关节的控制量输入.每个周期在更新机器人最新构型后,循环执行差值等分,直至机器人运动到目标点和目标姿态.
3 仿真和试验
在仿真中,通过计算雅克比矩阵的条件数[13],给出了当s分别为不同数值、以及根据本文算法动态变化时,机械臂的运动范围,如图6所示.仿真过程中,机械臂末端期望Z坐标取固定值,机械臂期望姿态亦保持恒定不变,只针对XY平面进行分析比较;浅色区域表示机械臂在该点处奇异,深色区域表示机械臂在该点处存在唯一的逆运动学解;图中坐标系为机械臂基坐标系.
图6(a)是当UP支链的长度s=550 mm时,机械臂末端在XY平面上可达空间的奇异性情况;图6(b)是s=580 mm时的情况;图6(c)是s=600 mm时的情况;图6(d)是s=620 mm时的情况;图6(e)是s=650 mm时的情况;图6(f)是本文算法提出的s动态变化时的情况.可以看到,s的动态变化使得机械臂的可达空间实现了不同s情况下可达空间的集合,因而,也就增大了机械臂的运动范围.仿真结果证实了本文提出的轨迹规划算法的有效性.
在试验中,同样固定机械臂末端期望Z坐标和姿态,控制机械臂前伸,并对其前伸轨迹进行分析.图7记录了前伸过程中,机械臂末端X、Y坐标在机械臂基坐标系下的轨迹.

图7 机械臂末端轨迹Fig.7 Manipulator end-effector trajectory
从图7中可以看到,机械臂沿着X方向前伸了大约410 mm,而从图6的机械臂XY平面可达空间上可以看出,当机械臂前伸(末端Y坐标从350 mm变为380 mm过程条件下)时,无论UP支链的长度s固定为何值,沿着X方向的可移动距离大概都在320 mm左右,而本文提出的轨迹规划算法可使机械臂沿X方向的移动距离超过500 mm,大大增加了其运动空间.
此外,还在大型花岗岩平台上,利用6自由度气浮台、手眼双目相机等设备,进行了空间操作抓捕全物理试验.试验结果表明本文轨迹规划算法明显提高了抓捕机械臂的运动能力.
4 结 论
本文通过将7自由度串并混联机械臂的UP支链伸长量固定,将其等效为一个6自由度形式的串联机械臂,进而得到解析的逆运动学反解.在规划过程中,又将UP支链伸长量进行了释放,提出了一种基于解析解的全自由度轨迹规划算法.
解析解的存在,保证了规划算法的实时性,将为以后引入力控制等复杂策略奠定基础;而全自由度轨迹规划则在最大程度上扩大了串并混联机械臂的可达空间.
试验结果表明,本文算法在保留串并混联机械臂承载能力强、结构紧凑的优点之上,使机械臂的规划可达空间大大提升,客观上提升了对目标星进行抓捕和连接的能力,在未来空间机械臂在轨维修维护任务中具有广泛的应用前景.
[1] STOLL E, LETSCHNIK J, WALTER U,et al. On-orbit servicing[J]. IEEE Robotics and Automation Magazine, 2009,16(4): 29-33.
[2] YOSHIDA K. Engineering test satellite VII flight experiments for space robot dynamics and control: theories on laboratory test beds ten years ago, now in orbit[J]. The International Journal of Robotics Research,2003,22(5): 321-335.
[3] WEISMULLER T, LEINZ M. GNC technology demonstrated by the orbital express autonomous rendezvous and capture sensor system[C]//The 29thAAS Guidance and Control Conference, Breckenridge, CO, USA: AAS, 2006:6-16.
[4] BROOK S, DAVID B. DARPA Phoenix payload orbital delivery (POD) system: “FedEx to GEO”[R]. San Diego, USA: AIAA, 2013.
[5] WALDRON K J, HUNT K H. Series-parallel dualities in actively coordinated mechanisms [J]. The International Journal of Robotics Research, 1991,10(5): 437-480.
[6] ROTH B, WALDRON K J, RAGHAVAN M. Kinematics of a hybrid series-parallel manipulator system [J]. Journal of Dynamic System, Measurement, and Control, 1989,111: 211-221.
[7] ZOPPI M, ZLATANOV D, Molfino R. On the velocity analysis of interconnected chains mechanisms[J]. Mechanism and Machine Theory, 2006,41(11): 1346-1358.
[8] PAPADOPOULOS E. On the dynamics and control of space manipulators [D]. Cambridge:Department of Mechanical Engineering, Massachusetts Institute of Technology, 1990.
[9] SLOTINE J J E, LI W. Composite adaptive control of robot manipulators [J]. Automatica, 1989, 25(4): 509-519.
[10] FOURQUET J Y. Optimal control theory and complexity of the time optimal problem for rigid manipulators [C]// Proceedings of the IEEE/RSJ Conference on Intelligent Robots and Systems, Yokohama, Japan: IEEE Industrial Electronics Society, 1993,84-90.
[11] LATOMBE J C. Robot motion planning [M]. Norwell: Kluwer, 1991:22-37.
[12] SPONG M W, VIDYASAGAR M. Robot dynamics and control [M]. New York, USA: John Willey & Sons, Inc., 1989:57-94.
[13] 张贤达. 矩阵分析与应用[M]. 北京: 清华大学出版社, 2004:341-400.
Trajectory-Planning Algorithm for Series-Parallel Space Manipulator Based on the Full DOFs
WANG Yong1,2, TANG Qiang1,2, XU Shuanfeng1,2, ZHU Zhibin1,2,HE Yingzi1,2, WEI Chunling1,2
(1.BeijingInstituteofControlEngineering,Beijing100190,China;2.ScienceandTechnologyonSpaceIntelligentControlLaboratory,Beijing100190,China)
There are few researches so far focusing on the series-parallel manipulator for space manipulators, where also the trajectory-planning algorithms are usually without resort to the redundant DOFs. This paper proposes a novel trajectory-planning algorithm for a 7 DOFs series-parallel space manipulator, which is based on the analytical solutions of the inverse kinematics, and makes use of all the 7 DOFs. The algorithm enlarges the reachable space of the manipulator, ensures real-time implementation of the planning, and also maintains the high load capacity due to the series-parallel structure. These facilitate the series-parallel space manipulator to capture the targets during the space operation. Through simulations and experiments for space operation on the ground, the efficiency of the algorithm is verified.
space Robot; space operation; trajectory-planning; series-parallel; redundant DOFs
*重点实验室基金资助项目(9140C59020611HT05).
2015-05-29
TP241.3
A
1674-1579(2015)05-0013-06
10.3969/j.issn.1674-1579.2015.05.003
王 勇(1982—),男,工程师,博士,研究方向为空间机器人在轨操作控制技术,移动机器人建图、定位、路径规划、导航技术等;唐 强(1981—),男,工程师,博士,研究方向为空间机器人在轨操作控制技术,高稳定度航天器控制技术,高速、高精度机器人运动控制技术等;徐拴锋(1983—),男,工程师,博士,研究方向为空间机器人在轨操作控制技术,空间机械臂动力学与控制技术等;朱志斌(1981—),男,高级工程师,博士,研究方向为空间机器人在轨操作控制技术,地面试验验证技术等.

