中国系统重要性银行附加资本计提机制研究基于CopulaCoVaR模型

潘凌遥 蒋晓泉 费紫微

摘要：在CoVaR风险度量框架的基础上建立系统重要性银行附加资本计提机制，旨在将风险溢出与资本计提挂钩。运用Copula-CoVaR模型测算商业银行对银行体系的风险溢出效应，考虑到额外的资本对溢出风险吸收作用，在控制每一家银行对银行系统的风险溢出一致的基础上确定银行的资本充足水平，进而确定对应的系统重要性银行附加资本的计提比例。

关键词： CopulaCoVaR模型；风险溢出；系统重要性银行附加资本

中图分类号：F832.2文献标识码：A文章编号：1003-7217（2015）03-0023-06

一、引言

2008年肇始于美国并蔓延至全球的金融危机发生以后，各国监管当局都提出要加强宏观审慎管理，而宏观审慎管理的目标就是为了防范系统性风险。如何进行系统性风险防范受到了理论界和实务界前所未有的重视。国际货币基金组织、金融稳定理事会和国际清算银行（2009）认为，系统性风险是由于金融体系整体或局部受到破坏导致金融服务中断、对实体经济具有潜在负面影响的风险[1]。在《巴塞尔协议III》中规定银行必须构建资本防线应对系统性风险，其中就包括逆周期超额资本和系统重要性银行附加资本[2]。这两者都针对系统性风险，可以将其统称为系统性风险资本。

在内部评级法的视角下，资本与银行的风险大小直接挂钩，商业银行面临多大的风险就必须拥有足量的资本与之相匹配。《巴塞尔协议III》提出的逆周期超额资本和系统重要性银行附加资本虽然针对的都是风险，但是两者的计提是基于不同的计提框架，而且这些计提框架没有与系统性风险的大小挂钩，这会与商业银行经济资本管理产生矛盾[3]。

2014年12月9日，美联储推出了一项针对系统重要性银行附加资本要求的提案，根据系统重要性银行对金融系统带来的潜在风险，必须留存1%～4.5%的风险加权资产以应对潜在风险，即提出了1%～4.5%的附加资本要求。

可见，科学地测度银行业系统性风险，将商业银行附加资本的计提与该银行对银行业的系统性风险贡献对应起来是当前宏观审慎管理所需要解决的前沿问题。

根据研究视角的不同，系统性风险的测度方法大致可以分为以下几类：（1）基于宏观数据的测度方法。如KLR模型（Kaminsky、Lizondo & Reinhart，1998）[4]、FR模型（Frankel & Rose，1996）[5]等。Borio（2009）也构建了宏观经济早期预警指标，并用来预测银行部门危机发生的概率[6]。（2）基于银行间关联性的测度方法。IMF（2009）[7]在金融稳定报告中详细介绍了四种基于关联研究法的测量系统性风险的模型：网络传导分析法（Allen & Babus，2008）、共同风险模型法（Brunnermeier，2009）、困境依赖矩阵（Segoviano & Goodhart，2009）和违约强度模型法（Giesecke & Kim，2009）。（3）基于投资组合理论的测度方法。这种方法采用股票市场数据，把整个金融体系看作是各个金融机构组成的投资组合，用损失的波动（Avesani & Pascual，2006）[8]、风险价值VaR（Inui & Kijima，2005）[9]、期望亏损ES（Yamai et al，2005）[10]、条件风险价值CoVaR[11]、边际期望损失法（Brownlees & Engle，2010） [12]等来衡量系统性风险。（4）前瞻性的测度方法：未定权益分析法（CCA）（Gray，2007）[13]。

尽管金融危机以来对于系统性风险测量的方法研究取得了一定的的成果，但是由于系统性风险测量对数据和模型的要求很高，不能与商业银行的资本直接挂钩。CoVaR方法是最新提出的一种系统性风险度量方法，利用公开市场数据就能对商业银行的溢出效应进行度量。

值得注意的是，系统性风险首先是风险，它强调的是当银行受到冲击时对外部的造成巨大负面影响的概率。这种影响与银行的财务状况是分不开的。当银行具备较为稳健的财务状况，其抵御冲击的能力提高，进而对外界造成巨大负面影响的概率就会下降，系统性风险也就随之降低。资本覆盖风险，商业银行的风险溢出程度与资本充足情况紧密相关。当资本较为充足时，银行可以通过资本吸收外部冲击带来的损失，从而降低自身风险的溢出效应；反过来，当资本不够充足时，银行内部消化损失的能力明显不足，其风险的外溢效应也会随之增加。因此，银行可以通过计提额外的资本来降低风险溢出效应，减少其对系统的冲击。基于此，本文拟采用Copula-CoVaR模型来计提系统重要性银行附加资本。

二、CopulaCoVaR模型

（一）CoVaR模型

金融机构j的无条件风险价值VaR的定义为：

Pr （Xj≤VaRj）=q（1）

其中，Pr 表示概率，式（1）表示银行的损失Xj超过某一数值VaRj的概率为q。关于CoVaR，根据Adrian和Brunnermeier（2008）的定义，设有i，j两个金融机构，将此时的条件VaR值记为CoVaRj/iq，表示当i金融机构出现问题时，j金融机构的风险水平。用公式简单表示为：

Pr （Xj≤CoVaRj/C（i）q|C（i））=q（2）

其中，C（i）表示i金融机构的某些风险事件，q是分位点。CoVaRj/iq不仅包含了j金融机构自身的无条件风险价值VaRj，也包含了i金融机构对它的风险溢出效应。关于i金融机构对j的溢出效应ΔCoVaRj/iq可以定义为：

ΔCoVaRj/iq=CoVaRj/Xi=VaRiq-VaRj（3）

商业银行内部评级法中关于资本要求的计算，是根据银行在一定置信水平下无条件风险价值与预期损失的差额来确定。CoVaR模型能较好地将风险溢出效应与无条件风险价值放在同一计算框架内，使较为准确地计提系统重要性银行附加资本成为可能。

（二）Copula连接函数

Copula函数簇是一类将各研究对象的联合分布与各对象的边缘分布连接在一起的函数。它可以反映较为复杂的多元分布，并将多元分布分解为多个边缘分布与一个Copula函数的形式。Copula理论最早是Sklar1959年提出，他认为可以将一个联合分布分解成k个边缘分布和一个Copula函数，Copula函数描述了变量之间的相关性。

根据多元Sklar定理，如果F（·，…，·）为具有边缘分布F1（·），F2（·），…，FN（·）的联合分布函数，那么存在一个Copula函数C（·，…，·），满足：F（x1，x2，…，xN）=C（F1（x1），F2（x2），…，FN（xN））。

如果F1（·），F2（·），…，FN（·）是连续的，则C（·，…，·）唯一确定；反之，如果F1（·），F2（·），…，FN（·）为一元分布，C（·，…，·）为相应的Copula函数，那么由上式定义的F（·，…，·）为具有边缘分布F1（·），F2（·），…，FN（·）的联合分布函数。

同时，也可以得到多元分布的概率密度函数：

f（x1，x2，…，xN）=c（F1（x1），F2（x2），…，FN（xN））∏Nn=1fn（xn），其中，c（u1，u2，…，uN）=C（u1，u2，…，uN）u1u2…uN，fn（xn）是边缘分布Fn（xn）的密度函数，n=1，…，N。

财经理论与实践（双月刊）2015年第3期2015年第3期（总第195期）潘凌遥，蒋晓泉等：中国系统重要性银行附加资本计提机制研究基于CopulaCoVaR模型

（三） CoVaR的计算

根据CoVaR模型中关于CoVaR值的计算，是当i金融机构出现问题时，j金融机构的风险水平。

若收益率序列Xi，Xj，概率密度函数分别为fi（xi），fj（xj），它们的联合概率密度函数为f（xi，xj），此时Xi的条件密度函数为：

fi|j（xi|xj）=f（xi，xj）fj（xj）（4）

将Copula函数与式（4）相结合，进一步可以得到：fi|j（xi|xj）=c（Fi（xi），Fj（xj））fi（xi）fj（xj）fj（xj）=c（Fi（xi），Fj（xj））fi（xi），此时i金融机构的CoVaR值可以通过反解式（5）得到。

∫q-∞CoVaRi|jc（Fi（xi），Fj（VaRjq））fi（xi）dxi=q（5）

三、风险溢出效应度量

（一） 数据来源与数据预处理

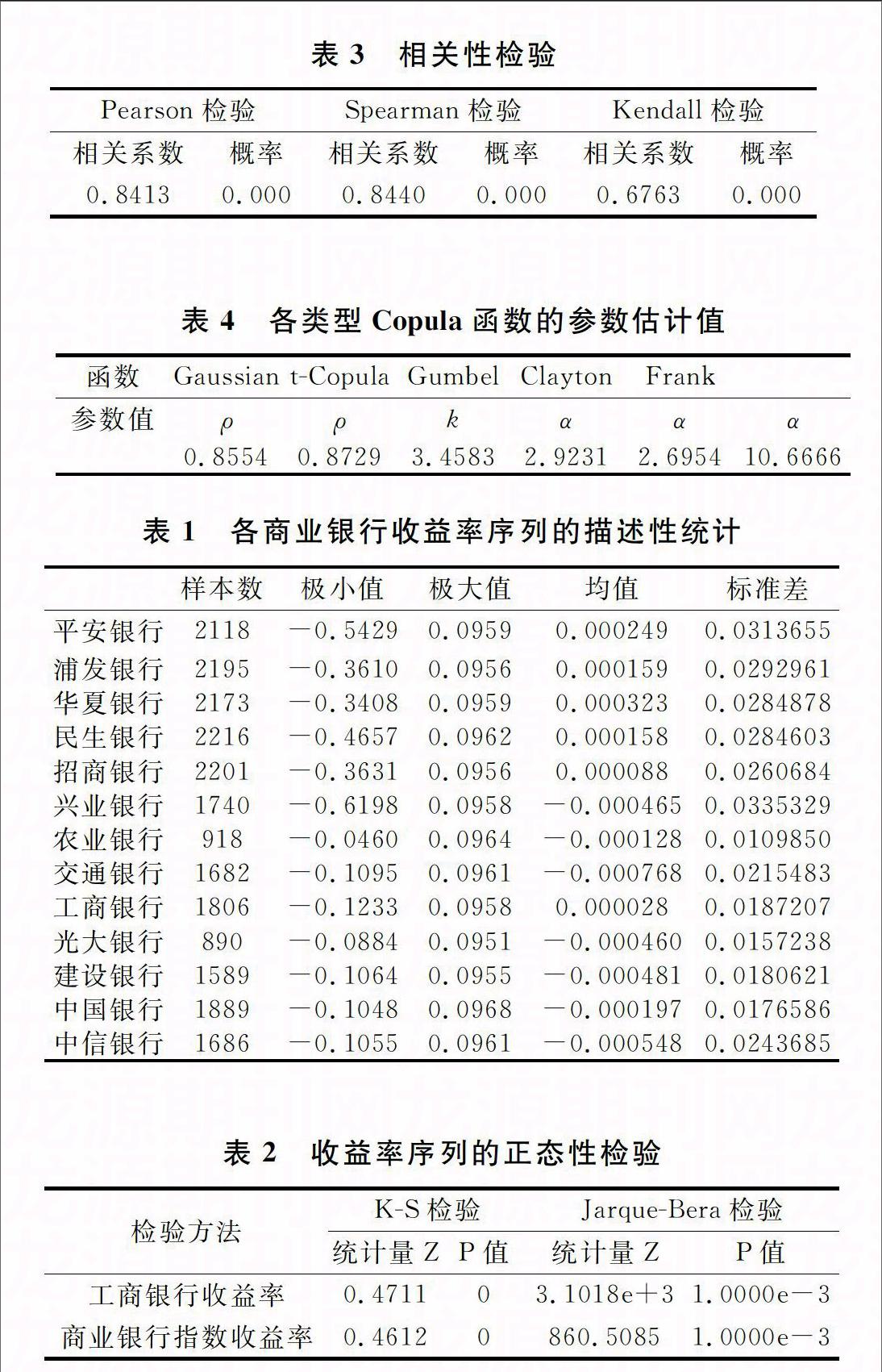
在计算风险溢出效应之前，首先要确定各上市银行与商业银行指数之间的相依结构。考虑到宁波银行、南京银行、北京银行是城市商业银行，其余13家为全国性商业银行，就资产规模而言，2014年一季度规模最大的城商行北京银行的资产为规模最小的股份制商业银行平安银行的60%，此外，13家商业银行的总资产占全国所有银行资产的78.02%，故选择这13家银行作为系统重要性银行附加资本计提的分析样本。为了能使数据更好地反映银行收益率变化情况，选取13家上市银行2005年1月～2014年5月股票市场日收盘价数据。衡量银行体系整体的指标选用WIND数据库中的商业银行指数数据，其成分为16家上市银行，通过对股票价格赋予一定的权重计算得到。上市银行的日收益率μt=ln Pt-ln Pt-1，Pt为该日的收盘价，各收益率序列的描述性统计如表1所示，商业银行指数的收益率随后也作相同处理。

（二） 相关性检验

采用Pearson相关性检验、Spearman秩相关检验和Kendall秩相关检验对工商银行收益率序列以及商业银行指数收益率序列的相关性进行分析，结果如表3所示。

从表3可以看出，三种相关性检验的P值都为零，表明两个收益率序列之间存在十分显著的相关关系，同时相关系数均为正值且较大，说明工商银行的收益率序列与商业银行指数收益率序列正向相关。

（三）Copula函数估计

Copula函数有很多，需要在这些Copula函数中选出最合适的来描述工商银行收益率序列以及商业银行指数收益率序列的边缘分布的相依结构。选择5种常用的Copula函数，包括椭圆型Copula函数族中的GussianCopula和tCopula，以及阿基米德Copula函数族中的GumbelCopula、ClaytonCopula和FrankCopula，来拟合二个收益率序列的联合分布。另外，拟合函数与原始序列之间的平方欧式距离越小能表明拟合效果越佳，因此，通过计算各类型Copula拟合函数的平方欧式距离来筛选最优拟合函数。不同Copula函数拟合的参数估计值如表4所示。

10.6666其中，ρ为线性相关系数，k为自由度，α为阿基米德函数族中的参数。在得到这些参数的基础上，进一步考察这些函数的拟合效果。

如果（xi，yi）是二维联合分布（X，Y）的样本点，记X和Y的经验分布函数为Fn（x）和Fn（y），此时样本的经验Copula函数如下：

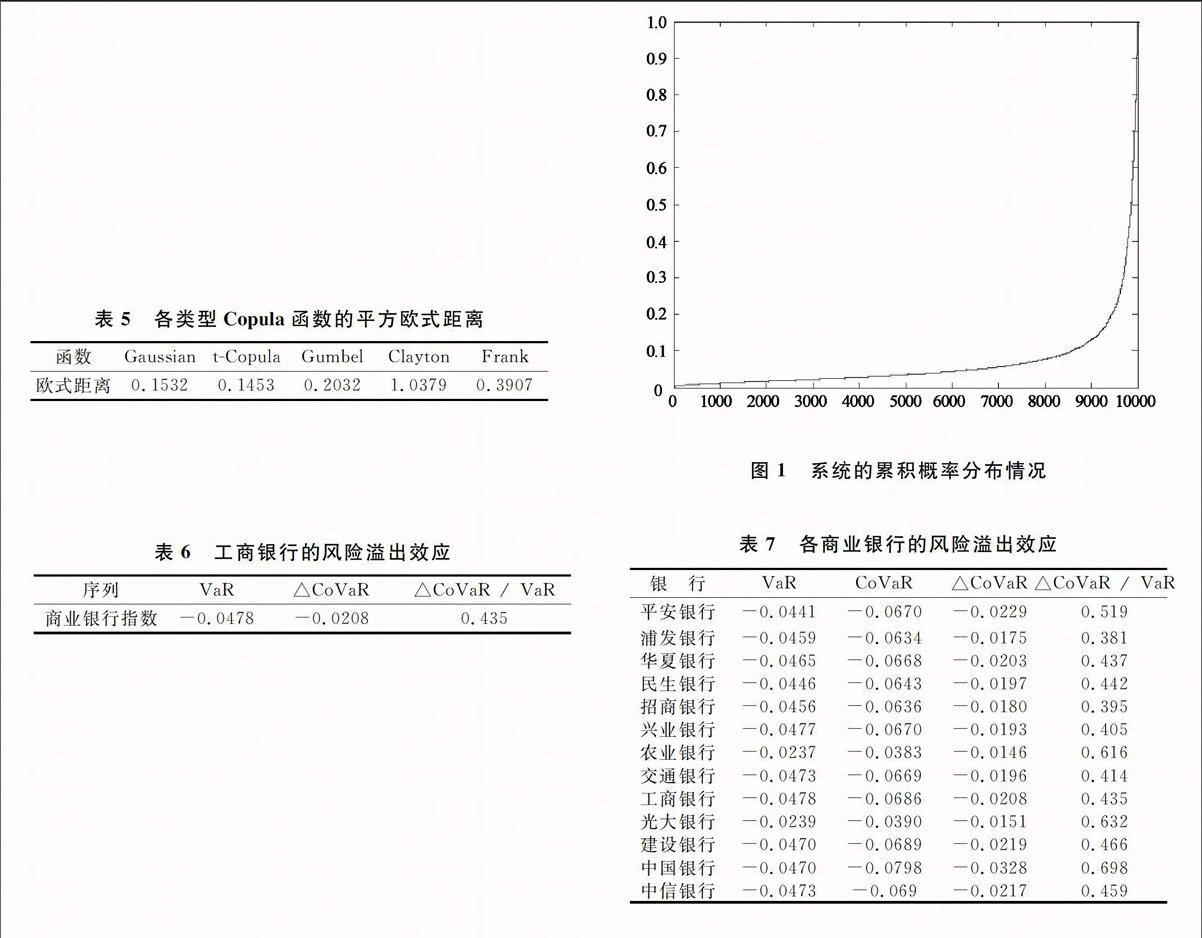
函数的平方欧式距离如表5所示。

平方欧式距离越小，表明Copula函数的拟合效果越好。从表5可知，tCopula函数的平方欧式距离最小，拟合优度最高，故将其作为衡量工商银行收益率与商业银行指数收益率联合分布的Copula函数。

（四）CoVaR的计算

在考虑风险溢出效应的时候，考察的时点是当银行出现危机的时候，而银行出现危机的情况一般用较为极端的分位点表示，一般可以选用1%、2.5%、5%等分位点，考虑到样本的大小以及从表1中体现出来的收益率数据异常情况可能会对结果造成影响，本文选用2.5%分位点来计算风险溢出效应。根据上述tCopula函数的参数估计结果，采用Monte Carlo模拟来计算工商银行对整个系统的风险贡献。第一步，根据随机生成满足上述tCopula函数的两列概率序列，每一序列含有1000个数据；第二步，筛选出当工商银行处于2.5%的分位点时，整个系统的累积概率值；第三步，重复上述过程10000次。由此，就得到了当工商银行处于危机状态下整个系统的累积概率的分布情况，按从小到大排列后得到图1。根据CoVaR的定义，当工商银行处于危机时，整个系统在分位点2.5%的累积概率为0.0060，根据商业银行指数的原始收益率序列可以计算出相应的收益率值，进一步就可以得到工商银行对整个银行体系的系统性风险贡献为43.5%。（五）各商业银行的风险溢出效应

与工商银行的算法相同，可以得到另外12家上市商业银行的风险溢出效应。从表7可以发现，风险的溢出效应在各银行之间存在较大的区别，风险溢出水平最低的是浦发银行，仅为38.1%，风险溢出水平最高的是中国银行为69.8%，测算过程中还出现工商银行、建设银行的风险溢出较平安银行低的现象。银行的资本是用来覆盖风险的，资本充足情况的不同就会导致风险溢出情况存在差别。根据各商业银行2013年半年报和年报，平安银行的资本充足水平仅为8.78%和9.9%，而工商银行和建设银行的资本充足率都超过了13%。也就是说，工商银行和建设银行可以利用超额的资本内部消化风险，减少风险溢出效应，因此才会出现诸如上表的情形。如果平安银行的资本充足率达到与工商银行一个水平，那么，它的风险溢出将会大大降低。

四、商业银行系统重要性银行附加资本的计提

上面的分析给了我们一个启示，在用CoVaR模型测算商业银行风险溢出的时候，银行的资本充足情况对风险溢出效应存在较大的影响，因此，在考察系统重要性银行附加资本计提的时候要控制各商业银行具有相同的风险溢出水平。

我们将各商业银行的风险溢出水平控制在零溢出计算各商业银行的资本充足情况。零溢出也就意味着此时的CoVaR就是各商业银行所对应的银行系统VaR值，根据银行系统VaR值找出相应的原始序列的分位点，并读取该点的收益率值。

具体的求解思路如下：

第一步，与前面的模拟过程一样，根据最优的Copula函数随机产生符合条件的累积概率u（x），v（y），每次产生10000组数据，这一过程模拟1000次；

第二步，每一次模拟v（y）都按照u（x）的大小进行排序；

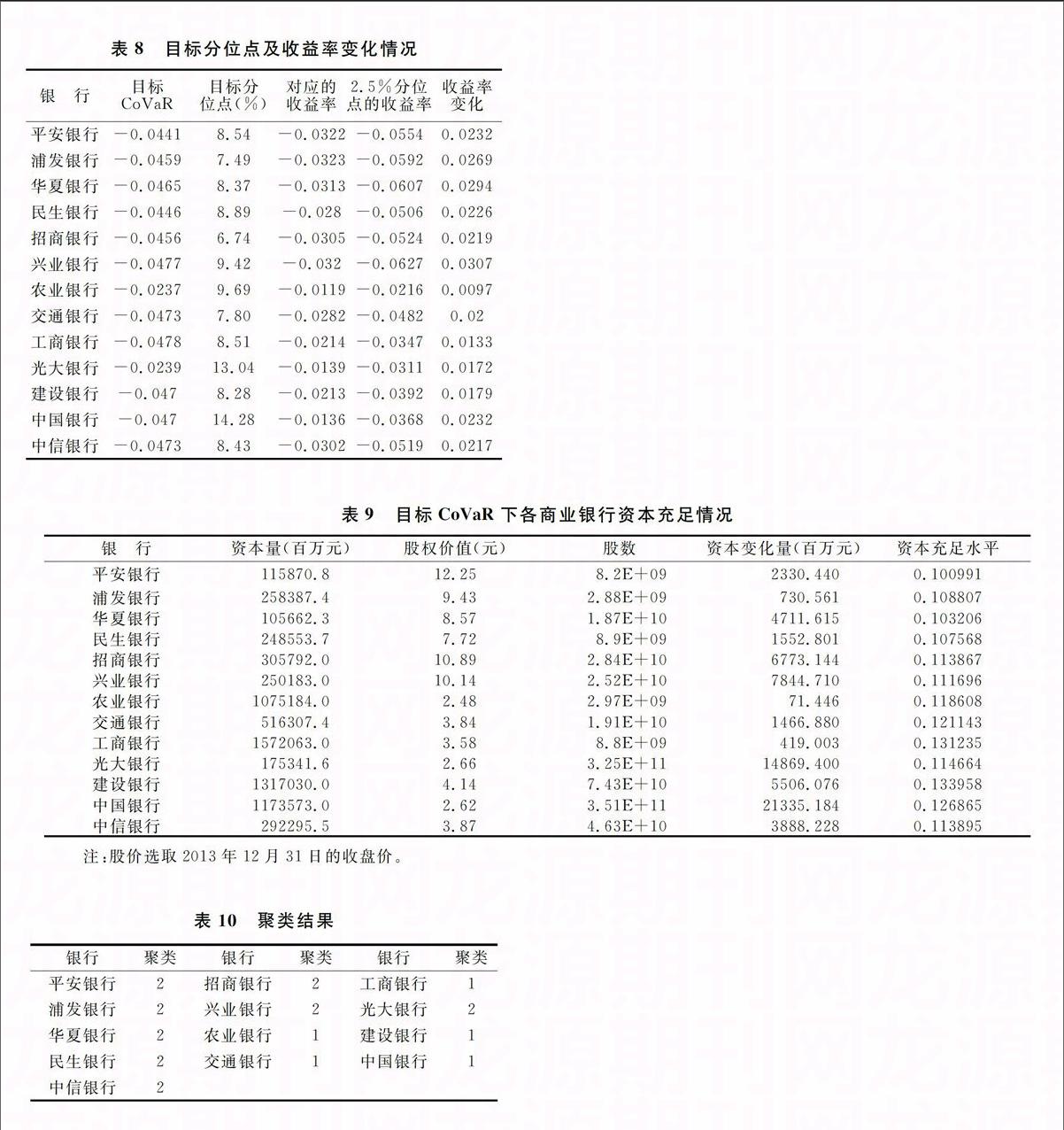
第三步，对每一分位点上的u（x），读取2.5%分位点的v（y），依照模拟过程，这样的v（y）共有10000个，将该序列记为p；第四步，对p中的序列值编号为1～10000，将目标CoVaR在序列p中找出，对应的编号与10000比值就是u（x）的目标分位点；第五步，在原始收益率序列中读取目标分位点的值。计算结果如表8所示。

1.对2013年商业银行的系统重要性银行附加资本进行计算。重点是如何将收益率的变化与银行资本结合起来，考察在目标CoVaR下银行的资本充足水平。用收盘价来表示银行的股权价值，当控制银行的风险溢出效应的比例时，银行股票收益率的变化乘以股票收盘价就能直接计算出股权价值的变化，而股权价值的变化量就是商业银行需要计提的系统性风险资本。计算结果如表9所示。可以得到银行零风险溢出时，上市银行新的资本充足水平，从而可以对系统重要性银行附加资本进行综合有效评估。根据表9所示，国有股份制商业银行比其他股份制银行需要更高的系统重要性银行附加资本。

采用K均值聚类对表9的资本充足水平进行分类，结果见表10。聚类的结果表明，系统重要性第一梯队包括建设银行、工商银行、中国银行、交通银行和农业银行，剩下的银行都属于第二梯队。对于我国而言，不仅仅上市银行存在系统性风险，只能说风险较为集中于这些银行，为了能控制系统性风险的累积，进而防止危机的发生，不管是第一梯队还是第二梯队的银行都应该为自身溢出的风险负责。

2.根据商业银行零风险溢出的情况来确定系统重要性银行附加资本计提机制。最优的系统重要性银行附加资本计提自然是能甄别银行的不同风险状况，针对不同银行进行差异化的系统性风险资本计提，有多大的风险溢出就计提相应的资本。但监管的一个原则就是要简单明了，操作简便，因此，我们根据上面两种分类来确定系统重要性银行附加资本比例。

以第二梯队为例，将第二梯队的银行看成一个整体，在零风险溢出的情况下，整体的资本等于新的资本充足水平与各银行风险加权资产乘积之和。系统性风险资本的计提，就是要在8%的最低资本充率要求与2.5%留存超额要求的基础上，也就是说在10.5%的资本充足水平基础上进行计提。采用的方法是当第二梯队的银行同时提高一定比例的资本，使得它们的资本之和与零风险溢出情况下整体的资本接近。控制精度在0.1%，通过matlab编程可以计算得到第一梯队和第二梯队的系统重要性银行附加计提比例如表11。

与《巴塞尔协议III》规定的一样，系统重要性银行附加资本必须是商业银行的普通股资本。我国《商业银行资本管理办法（试行）》要求商业银行满足5%的普通股最低要求，2.5%的储备资本要求，这就使得商业银行的普通股比例要达到7.5%，外加系统重要性银行附加资本，这也就意味着第一梯队商业银行的普通股最低要求要达到9.73%，而第二梯队商业银行要达到8.03%。

五、结论

系统性风险的度量是一复杂的系统工程，对其准确的度量还有很长的路要走，而以防范系统性风险为目的的宏观审慎管理框架体系的构建和完善仍存在颇多阻碍。本文的主要工作是依托CoVaR风险度量框架，将商业银行风险溢出效应与商业银行的资本结合起来，体现了资本覆盖风险的理念，弥补了系统重要性银行附加资本计提不与系统性风险大小对应的不足，为系统重要性银行附加资本的计提提供依据。

这一系统重要性银行附加资本计提框架是开放的，随着商业银行数据的积累，运用Copula-CoVaR模型可以考虑更为极端的情形来捕捉系统性风险。监管当局也可以根据经济形势如果认为零溢出对于银行体系而言过于严格，可以控制风险溢出的比例为某一合理正值，减小银行资本补充压力来刺激经济增长。随着监管技术的进步和监管人员素质的提高，监管当局可以采用更差异化的方法实现系统性风险计提，实现对每一家银行确定系统重要性银行附加计提比例。

参考文献：

[1]FSB. Guidance to assess the systemic importance of financial institutions， markets and instruments： initial considerations[J]. Report to G20 Finance Ministers and Governors， 2009.

[2]Basel Committee on Banking Supervision. Basel Ⅲ：A global regulatory framework for more resilient banks and banking systems [OL]， 2010. www.bis.org/publ/bcbs189_dec2010.pdf.

[3]彭建刚，潘凌遥. 关于商业银行资本协调管理的几个问题[J]. 湖南大学学报（社会科学版），2014，（3）：36-40.

[4]Kaminsky G L， Lizondo S and Reinhart C M. Leading indicators of currency crises[R]， IMF staff paper， 1998.

[5]Frankel J A， Rose A K. Currency crashes in emerging markets： An empirical treatment[J]. Journal of international Economics， 1996， 41（3）： 351-366.

[6]Borio C. Implementing the macroprudential approach to financial regulation and supervision[J]. Financial Stability Review， 2009 （13）： 31-41.

[7]International Monetary fund. Global Financial Stability Report： Responding to the Financial Crisis and Measuring Systemic Risks[M]. World Economic and Financial Surveys，2009.

[8]Pascual A G， Li J. A new risk indicator and stress testing tool： A multifactor Nthtodefault CDS basket[M]. International Monetary Fund， 2006.

[9]Inui K， Kijima M， Kitano A. VaR is subject to a significant positive bias[J]. Statistics & probability letters， 2005， 72（4）： 299-311.

[10]Yamai Y， Yoshiba T. Valueatrisk versus expected shortfall： A practical perspective[J]. Journal of Banking & Finance， 2005， 29（4）： 997-1015.

[11]Adrian T， Brunnermeier M K. CoVaR[R]. National Bureau of Economic Research， 2011.

[12]Brownlees C， Engle R. Volatility， correlation and tails for systemic risk measurement[J]. Working paper， New York University Stern School of business， 2010.

[13]Gray D F， Merton R C， Bodie Z. New framework for measuring and managing macrofinancial risk and financial stability[R]. National Bureau of Economic Research， 2007.

（责任编辑：宁晓青）