宏观审慎政策与银行风险承担研究
沈沛龙++王晓婷

摘要:针对宏观审慎政策中的逆周期政策工具对银行风险承担产生的影响进行了分析。在理论上研究了逆周期政策工具所带来的宏观和微观效应,并运用动态面板数据广义矩估计方法进行了实证分析。研究发现,在信贷扩张期杠杆率、贷款损失准备金率的上升会使银行的当期风险承担水平增加,资本充足率的提高使风险承担降低。而滞后六个月的资本充足率、杠杆率、贷款损失准备金率的上升可以显著降低当期的风险承担水平,宏观审慎政策工具的宏观效应和微观效应一致。
关键词: 宏观审慎政策;银行风险承担;逆周期;广义矩估计
中图分类号:F832.2文献标识码:A文章编号:1003-7217(2015)03-0009-07
一、引言
2008年美国金融危机爆发后并迅速蔓延,暴露了对金融系统稳定性负责的全面政策框架的缺失。危机后国际金融监管组织和各国监管当局开始制定和实施以降低金融体系系统性风险为目标的宏观审慎政策。
宏观审慎政策的作用机理即通过一系列的政策工具影响个体金融机构的资产负债表及其经营策略,从而作用于金融机构的信贷供给,进一步影响信贷供给总量及价格,以达到减少系统性风险的目的。宏观审慎政策工具及监管标准都是针对个体金融机构制定的,这些宏观审慎政策工具在消除金融体系顺周期性和跨部门风险的同时,对个体金融机构的风险承担也会产生一定的效应与影响。宏观审慎政策的宏观效应与微观效应是否一致及微观效应能否促进宏观效应的实现,并达到减小金融体系的顺周期性和降低系统性风险的目的,仍是理论界关注的重要问题之一。本文试图通过采用改进后的贷款组合信用风险模型与差分GMM模型从理论与实证两方面对宏观审慎政策工具对银行风险承担产生的具体影响与效应进行分析,从而进一步考察宏观审慎政策微观效应与宏观效应之间的关系,为更好地保障宏观审慎政策的实施效果提供理论依据。
二、文献综述
“宏观审慎”一词产生于1979年6月召开的库克委员会,会议中讨论了关于向发展中国家提供贷款能否影响其宏观经济和金融系统稳定性的问题。而“宏观审慎政策”则最早出现在1986年4月国际清算银行(BIS)关于国际银行业金融创新的报告中,该报告指出宏观审慎政策针对由金融创新造成的衍生品市场和证券市场相互关联的问题,促进了金融体系和支付机制的安全和稳健(BIS,1986)[1]。此后,此概念逐步发展为防范顺周期与跨部门两个维度的风险(Borio,2001)[2]和金融体系系统性风险(Crockett,2000)[3]的政策框架。
宏观审慎政策主要是为了防范金融体系的系统性风险及其对实体经济的溢出效应,并主要通过资本管理控制多个金融机构面临共同冲击时所造成的资产负债表萎缩而带来的社会成本(Hanson et al,2010)[4]。
宏观审慎政策工具虽然目的在于增强金融体系的稳定性,但也会影响到金融市场参与者的动机和行为,进而影响个体金融机构的风险承担。就此而言,Jokipii & Milne(2009)认为风险承担取决于资本缓冲的大小,资本和风险的关系取决于银行持有的资本高于监管要求的数量。当资本缓冲较低时,银行需要寻找到更多的资本的同时降低了风险承担,银行有大量资本缓冲时就会提高风险承担[5]。Terhi & Alistair(2010)运用GMM模型对1986~2006年美国银行业数据分析后发现,资本缓冲和银行风险承担存在正相关关系[6]。Cordella & Pienknagura(2013)运用模型分析了不同宏观审慎政策工具最低资本要求、存款税等政策工具对单个银行风险选择的影响,认为最低资本要求的提高、存款税的附加和流动性工具的实施降低了银行的风险承担[7]。宋琴和郑振龙(2010)提出资本与银行风险承担同市场集中度有关,市场集中度低时资本监管可以降低银行的风险承担[8]。从微观效应来看,刘胜会(2011)认为宏观审慎政策会从微观方面影响到银行的收入结构、资本运营、风险控制等经营策略[9]。
目前,有关宏观审慎政策对个体银行风险承担影响的文献主要集中于研究单一政策工具对银行风险承担的影响,且忽略了不同经济周期阶段政策工具对风险承担影响可能有所差异这一事实[10,11]。本文试从理论和实证两方面研究宏观审慎政策中逆周期资本缓冲、最大杠杆率和动态贷款损失准备金三个逆周期政策工具在不同周期阶段对银行风险承担所产生的影响。
三、宏观审慎政策工具的宏观效应和微观效应
宏观审慎政策工具虽然以其宏观效应的实现为主要目标,但对个体银行所产生的微观效应也不容忽视。目前,宏观审慎政策工具主要包括针对金融系统顺周期性的逆周期政策工具和针对跨部门风险而制定的对系统重要性金融机构及影子银行体系管理的一系列政策工具。以下针对逆周期政策工具的宏观及微观效应进行理论分析,并考察其宏观和微观效应是否具有一致性。
(一)逆周期政策工具
虽然在逆周期政策中所包含的政策工具目前还没有统一定论,但运用银行资本、杠杆率和贷款损失准备金等工具实施逆周期管理已受到广泛认可[12]。本文以中国银监会于2011年在《关于中国银行业实施新监管标准的指导意见》中提出的杠杆率、逆周期资本缓冲和动态贷款损失准备金三种主要政策工具为分析对象进行研究。
逆周期政策中对资本的要求主要包括超额留存资本和逆周期资本缓冲。巴塞尔委员会、国际会计准则委员会积极制定前瞻性的计算预期损失的方法,通过预期损失准备金来减轻金融体系的顺周期性。目前中国银监会也鼓励金融企业运用动态拨备原理,采取逆周期计提办法,以达到增强财务缓冲能力和吸收损失的目的。杠杆率是商业银行特定资本与调整后资产的比率,反映了银行自有资金和负债之间的关系,是衡量银行风险的重要指标。对杠杆率的限制约束了银行高杠杆经营行为,减少了监管套利现象,从而降低银行风险。
财经理论与实践(双月刊)2015年第3期2015年第3期(总第195期)沈沛龙,王晓婷:宏观审慎政策与银行风险承担研究
(二)逆周期政策工具的宏观效应
逆周期政策通过在不同周期阶段对政策工具制定不同的监管标准,以降低金融体系的系统性风险及其对宏观经济的溢出效应,在经济上行时限制系统性风险的积累,并在经济下行时弥补损失限制系统性风险的扩张,通过缓冲器的作用达到熨平经济周期的目的,促进经济的稳定和持续发展。当信贷增长过快及经济周期处于扩张阶段时,通过用超额资本和超额贷款损失准备金抵御潜在损失,并运用杠杆率限制银行资产的过度扩张;当信贷周期处于紧缩阶段时,银行运用自身资本吸收损失缓冲风险,而无需大规模减少资产以阻断信用创造功能。因此,无论经济周期扩张还是紧缩阶段,逆周期政策工具都可以起到稳定器的作用。严格审慎的监管标准会减小经济周期的幅度,从而使金融机构稳健运行,并使实体经济的产出波动减小。而且,一个稳健的银行体系不易陷入困境遭遇危机。总之,不论在信贷发展的扩张还是收缩阶段,逆周期政策都能降低系统性风险。
(三)逆周期政策工具的微观效应
在宏观审慎政策工具的宏观效应中,每种工具在经济周期的上行和下行阶段都能降低其风险,那么,这些政策工具在微观层面对银行的风险承担又会有何影响?下面从理论上分析逆周期政策工具在微观方面对单个金融机构风险承担的作用。
本文借鉴Ariccia et al(2010)提出的贷款组合信用风险模型,该模型从信贷渠道考虑银行通过有成本的监管来降低信贷风险[13],在其基础上加入了当实施逆周期政策时,资本要求、杠杆率及贷款损失准备金的变化对银行风险承担的影响。
中国银行业市场由于进入具有一定壁垒,经营业务差别较小,接近于垄断竞争市场,所以,本文基于垄断竞争市场假设对其进行分析。垄断竞争银行面临斜率为负的需求曲线:
l=s-drl(1)
其中l为贷款总量,s为金融市场的借贷总需求,rl为银行的贷款利率,d为贷款对利率的敏感度。
引入新变量贷款偿还比例q代表银行的管理水平,银行通过提高管理水平增强贷款偿还的可能性,贷款偿还比例q越大,则银行风险承担越小,所以,假设银行贷款每单位管理成本为12cq2(其中c为系数,q∈[0,1])。
假设银行的资金来源为存款和资本,资本在其中占比为k,存款占比为1-k。不实施宏观审慎政策时,考虑最低资本要求时银行利润为:
P1=q1[r1-rd(1-k)]-rck-(1-q1)m-cq212(s-dr1)(2)
其中rl为存款利率,rd为贷款利率,rc为资本成本率,m为贷款损失准备金计提率。当利润最大化时,由P1q1=rl-rd1-k+m-cq=0,得:q*1rl-rd1-k+mc。可以看出,银行风险承担主要与存款利率、贷款利率、资本占比及贷款损失准备金有关。
当实施逆周期政策时,考虑逆周期资本缓冲要求、动态拨备和杠杆率时,银行利润为:
P2={q2[r1-rd(1-k-h)]-rc(k+h)-
(1-q2)(m+n)-cq222}(s-dr1)(3)
其中h为逆周期资本缓冲政策中对资本的附加要求,n为对贷款损失准备金的附加要求,则(k+h)为杠杆率。
当利润最大化时,由P2q2=rl-rd1-k-h+m+n-cq2=0,得:q*2rl-rd1-k-h+m+nc。
通过以上分析过程可以看出,在经济周期的上行期,由于逆周期政策的实施,分子中h和k的存在,若贷款偿还比例增加,则银行的风险承担减少。但经济下行时,取消对银行的资本附加和拨备附加要求,如果资本量没有减少并补充损失,那么,银行就有动机持有高风险的资产,从而增加银行的风险承担。银行自身的风险承担则相对于经济周期上行时有所增加。但是,在上行期多计提的资本可以吸收由冲击带来的损失,同时保证银行不必为了维持一定的资本充足率而缩减资产和减少新贷款的发放。所以,逆周期政策的实施虽然在经济下行期加大了单个银行运营的风险承担,但从另一个角度提高了银行损失吸收能力并减轻了信贷中断现象,从而能够继续支持实体经济发展。
但如果回报不固定,只是追求特定资本结构下的利润最大化时,资本和风险承担存在正相关关系,由于银行资本数量是增加的,其风险偏好也在增加。所以,即使理论上资本的增加会降低银行的风险承担,但这一作用还需通过实证分析进行验证。贷款损失准备金和逆周期资本缓冲吸收损失的原理类似,只是损失准备金抵御的是预期损失,而资本抵御的是非预期损失。但当经济环境突然发生变化时,无法准确界定损失属于预期损失还是非预期损失。所以,损失准备金对银行风险承担的作用也需进一步认定。
同时,理论模型仅解释了政策工具对当期银行风险承担的影响,但逆周期政策是以滞后期为出发点设计的,所以,滞后期对风险承担的影响还需通过实证分析。
四、宏观审慎政策工具与银行风险承担实证分析
宏观审慎政策中的逆周期政策主要依靠信贷扩张或经济上行期积累的资本和准备金防范经济下行期的风险,所以,实证部分主要通过检验宏观审慎政策工具对未来时期银行风险承担的作用和信贷扩张期宏观审慎政策工具对当期风险承担的影响。根据中国银监会《关于中国银行业实施新监管标准的指导意见》的规定,中国银行业自2012年1月1日起实施包括逆周期资本缓冲、杠杆率和动态贷款损失准备金三个政策工具的新监管标准,现有银行公开披露资料中对宏观审慎政策工具的披露数据年份较少,所以,在实证部分通过分析银行在不同时期这三个政策工具和银行风险承担间的关系,推断宏观审慎政策工具可能对银行风险承担造成的影响,为实际宏观审慎政策的实施提供一定理论依据。
(一)变量选择
1.因变量。选用Z值和不良贷款率(nl)作为银行风险承担的因变量。借鉴Laeven & Levine(2009)的研究,银行的风险承担可以用代表银行距离破产的风险距离Z值来衡量[14]。Z值的计算公式为:
Z=ROA+C/Aσ(ROA) (4)
其中ROA为银行总资产收益率,C为资本总量,A为资产总量,σ为ROA的标准差。Z值越高则银行破产概率越小,经营状况越稳定。
不良贷款率为银行不良贷款总量占总贷款余额的比重。由于贷款业务目前仍是中国银行业的主要业务,不良贷款率是银行信贷资产安全性和信用风险的重要指标,选用不良贷款率作为银行风险承担变量具有一定合理性。
2.控制变量。
由于一国的宏观经济发展、货币市场和银行自身经营状况都可能会影响到银行的风险承担,所以,选取代表宏观经济发展情况的国内生产总值增长率(gdp)、代表货币资金存量的广义货币供给量(m2)、衡量银行间资金供求变化的银行同业拆借加权平均周利率(shibor)和代表银行规模的银行总资产值(size)及代表银行收益的总资产收益率(roc)作为研究宏观审慎政策工具对银行风险承担影响的控制变量。
3.解释变量。宏观审慎政策工具选用资本充足率(car)、杠杆率(l)、拨备覆盖率(npc)、贷款损失准备金率(p)及代表中国信贷周期的虚拟变量(d)。
虚拟变量根据巴塞尔委员会公布计提逆周期资本办法(BCBS,2010)计算的中国信贷周期[13],同时引入交叉项d×car、d×l、d×p检验信贷扩张期不同政策工具对银行风险承担的影响。
在判断实施逆周期政策的时间点及监管要求时,巴塞尔委员会在经过对数据指标大量分析和仔细论证之后,提出了逆周期政策应建立在信贷总额/GDP指标及偏离长期趋势程度基础上。巴塞尔委员会在对中国进行实证分析时,采用的是中央银行对金融业私营部门的所有信贷(BCBS,2010)[15],GDP值为名义GDP值,则:
R=CREDITGDP(5)
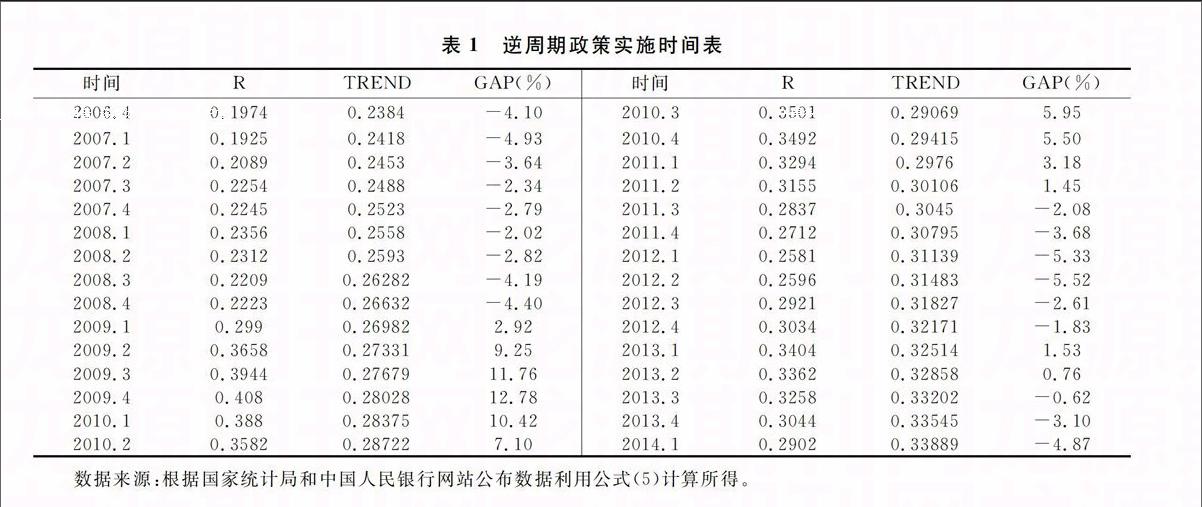
其中CREDIT为信贷总额。鉴于HP滤波方法可以对近期数据给予更高的权重,巴塞尔委员会建议使用高平滑参数(400000)的HP滤波法计算出R长期趋势TREND,并计算出其差值GAP。当GAP小于2%时则不需要计提逆周期缓冲资本;当GAP处于2%~10%之间时,GAP每提高1%,则多计提0.3125%的缓冲资本;当GAP大于10%时,则计提2.5%的缓冲资本。
为了增强数据的准确性,虽然在分析银行风险承担时采取的时间段是从2006~2013年的半年度数据,但对实施时间点的计算,采取了2002年4季度~2014年1季度共46个数据进行分析。表1中截取了2006年第4季度~2014年第一季度数据,结果显示我国需要实施逆周期政策的时间段为2009年第一季度~2011年第一季度,其余时间不需实施逆周期政策。(二)模型建立与实证分析
选取16家上市银行作为分析对象,但由于上市银行中的北京银行、南京银行、光大银行和农业银行披露数据年份较短,将其剔除。选取余下的12家银行对其2006年末~2013年末的半年度数据进行分析。
首先,对以上各解释变量、控制变量及因变量的相关性进行检验。对相关系数进行显著性分析发现,size和m2均与风险承担变量在10%水平上不显著,car与风险承担变量在10%水平上显著,其余变量相关系数均在5%水平显著,所以,在分析中将银行规模和货币供应量增长率两个变量剔除。另外,在进行初步回归分析时,发现多个解释变量和Z值的关系不显著,所以将Z值剔除,究其原因可能是数据长度较短,间隔时间较长,不符合Z值对数据长度的要求。同时,在分析选取的样本银行中,五家银行均被银监会认定为中国系统重要性银行,其余也均为上市银行,由于存在政府隐性担保和银行破产制度方面的缺失,银行破产可能性较小,所以,采用Z值分析也有一定的不合理性。
1.单位根检验与协整检验。
为了避免分析时出现伪回归现象,首先对面板数据进行单位根平稳性检验。分析采用了相同根单位根LLC检验和不同根单位根FisherADF检验两种单位根检验方式。表2为单位根检验结果,结果显示变量均为平稳序列,不存在单位根。
在单位根检验各变量均平稳后进行协整检验,以检验各变量间是否存在长期的均衡关系。协整检验结果见表3,对面板数据进行协整检验后得到4个统计量,Gt和Ga为组统计量,检验数据在异质性条件下是否存在协整关系;Pt和Pa为面板统计量,检验数据在同质性条件下是否存在协整关系。从表3可以看出,自变量car、l、npc与nl分别进行协整检验时都存在协整关系,而将car、l、npc和nl同时进行协整检验时则不存在协整关系。
2.模型建立及结果分析。
由于银行风险承担具有一定的延续性,会受到银行之前风险承担水平的影响,所以,在建立模型时将因变量的滞后一期变量作为解释变量来研究风险承担的延续性。由于在动态面板数据中,因变量的滞后一期作为解释变量会导致解释变量的内生性,而其他解释变量也存在潜在的内生性,所以,通过构建一组与内生解释变量相关而与随机扰动项不相关工具变量,以克服变量内生性所造成的估计偏差问题,进而得到稳健的估计结果。广义距估计(Generalized Method of Moment, GMM)是基于模型需满足的矩条件的参数估计方法,不考虑随机扰动项的准确分布,允许随机扰动项存在自相关和异方差等情况,且当样本量足够大时,估计渐进有效。
本文采用Arellano& Bond(1991)提出的差分GMM模型进行估计,差分GMM模型将动态面板数据模型进行差分后内生变量的滞后变量作为工具变量进行分析[16]。构建以下四个模型:
1注:括号内为Z统计量值,*、**、***分别表示在90%、95%、99%的置信水平下拒绝参数不显著的原假设。
数据来源:根据各银行年度报告、半年度报告,国家统计局、中国人民银行、上海银行间同业拆放利率网站数据计算所得。
对数据进行差分GMM回归,结果见表4。首先,检验引入的工具变量是否有效。由于模型中引入了内生变量的工具变量,需进行过度识别检验以检验模型中使用的工具变量是否外生及有效,表4最后一行显示,各方程的Sargan统计量均无法拒绝工具变量有效的原假设,即使用的工具变量有效。其次,检验是否可以用差分GMM模型进行估计。差分GMM模型所要满足的前提条件是扰动项不存在自相关,所以,要对扰动项进行相关性检验,表4中显示所有方程的扰动项均不存在二阶自相关,使用差分GMM模型估计是有效的。
对模型结果进行分析时,首先考察各控制变量和银行风险承担间的关系,gdp在方程(6)、(7)、(9)中都会显著影响到风险承担,且系数为负,说明在经济高速增长时期,银行的风险承担是降低的,而在经济下行期,由于贷款人信用及经营环境的变化,风险承担增加。Shibor对风险承担只有在方程(6)和方程(7)中显著,且系数均为正。Shibor作为银行间市场利率反映银行间市场的供求状况,Shibor的上升意味着银行间市场资金供不应求,亦即银行对短期流动性需求上升,意味着银行经营成本和流动性风险的上升,也会使银行的风险承担增加。Roc和银行风险承担的相关关系较弱,只有方程(9)在10%的显著性水平上相关,在一定程度上能解释风险和收益同向变化的现象。
接下来分析解释变量与银行风险承担间关系。4个方程的回归结果均显示滞后一期的nl可以在1%的显著性水平上影响当期的nl,且系数为正,说明银行的风险承担具有延续性,如果当前银行的风险承担增加,则六个月之后银行的风险承担也会增加。这是由于银行风险承担与其管理水平及经营策略有关,管理水平较好或风险偏好较低的当期银行风险承担较小,由于其管理政策的一致性,所以未来的风险承担水平也较小;反之管理水平较差和偏好风险的银行当前和未来的风险承担水平也都较大。说明若要银行未来风险承担水平降低,则要从当前管理策略入手,提高风险管理水平。
分析宏观审慎政策工具对银行风险承担影响时,观察政策工具对当期风险承担的影响。在整个分析期内,当期资本充足率和银行风险承担在方程(6)~(8)中都是呈同向变化的,资本充足率的上升意味着风险承担的增加。在信贷扩张期,宏观审慎政策工具对银行风险承担的影响主要观察d及交叉项car×d、l×d及p×d的系数。d的系数在方程(6)、(7)中为正,在方程(8)、(9)中为负,所以,无法直观定论信贷周期和风险承担的联系。car×d在方程(6)、(7)中显著为负,说明上行期资本充足率的提高意味着当期风险承担的降低。l×d及p×d系数均为正,说明上行期对杠杆率和损失准备金要求的提高会增加当期的风险承担。
在信贷扩张时期,资本充足率与杠杆率对风险承担的影响是不同的,资本充足率提高可以降低风险承担,而杠杆率的提高则会增加风险承担。资本充足率和杠杆率的区别在于其分母,资本充足率的分母为风险加权资产,是根据资产风险大小不同赋予不同权重而得到的风险加权资产,而杠杆率的分母为总资产。资本充足率提高,降低当期风险承担,可能是由于银行降低了风险资产持有数量而使风险承担降低。经济上行期,银行持有资产风险降低,在不变资本充足率要求下,银行会扩张业务,通过增持资产或冒险经营方式寻求利润最大化。而如果面临较高的资本要求,银行可减少风险加权资产的持有或增加资本来满足监管标准。减少风险加权资产的数量说明银行将风险级别较高的资产转换成风险级别较低的资产,或减少了高风险资产的持有,以此降低银行的经营风险。Das& N.R. Sy(2012)通过研究也发现,持有较少风险加权资产的银行在美国金融危机和欧债危机期间表现更好[17]。相反,资本的增加可能会引起风险的上升,而损失准备金的提高也会引起当期的风险上升。宏观审慎政策工具中逆周期资本要求和动态损失准备金要求在短期内会增加银行运营成本,降低个体银行的经营效率,削弱其竞争力。当银行面临资本需求时,会通过留存收益和发行股票或者减少贷款资产来提高资本水平,资本的增加意味着贷款息差同幅度地改变,高息差和更严格的贷款标准将减少家庭和企业的消费,在没有额外的非价格限制时,会增加银行的信贷成本。这些会降低银行的盈利能力和面临存贷息差上升的压力。在短期内银行会增加向借款人收取的利息或减少新增贷款的数量,银行贷款成本的增加和供给的减少会影响其利润。银行资本通过影响贷款净收益影响风险承担水平,为了维持一定的回报,银行会承担更高的风险,形成风险共担效应。
由于逆周期政策的原理是在上行期积累准备金和资本,在下行期使用。而经济环境变化往往是突然的,危机发生也是在较短时间内发生的。所以,在分析滞后期政策工具的微观效应时仅考察政策工具对滞后一期,亦即半年后银行风险承担的影响。除方程(9)中l(-1)外,在其余含有car(-1)、l(-1)、npc(-1)变量方程结果均显示变量系数显著为负,即滞后六个月的资本充足率、杠杆率、拨备覆盖率的上升可以显著降低当期的风险承担水平,这一结果为实施逆周期政策提供了依据。
综上分析,逆周期政策的实施并不会降低当前银行的风险承担水平,而会降低未来时期银行风险承担水平,与其政策目标一致。
五、结论
以降低金融体系系统性风险和减少金融体系对宏观经济溢出效应为目标的宏观审慎监管具有特有的宏观效应和微观效应。本文在理论研究部分对宏观审慎监管产生的宏观效应和微观效应进行了分析,在实证研究部分结合资本充足率、杠杆率和贷款损失准备金率这三个宏观审慎政策的代理政策工具,就宏观审慎政策工具对银行风险承担进行了分析。在宏观方面,宏观审慎政策可以通过在经济上行时限制系统性风险积累,经济下行时弥补损失,限制系统性风险的扩张,通过缓冲器的作用熨平经济周期。在微观方面,资本充足率、杠杆率和贷款损失准备金的提高会增加当期银行的风险承担,但显著降低了银行未来时期的风险承担,与其宏观效应具有一致性。综上所述,宏观审慎政策对银行风险承担的影响并不是体现在当前阶段,而是会降低未来时期银行的风险承担,宏观审慎政策工具的宏观效应和微观效应及其目标具有一致性。但对当期银行风险承担的监管和控制,并不能通过宏观审慎政策实现。
参考文献:
[1]Bank for International Settlements. Recent innovations in international banking[R]. Basel, April 1986.
[2]Borio,C, Furfine,C, Lowe,P. Procyclicality of the financial system and financial stability issues and policy options[R]. BIS Working Papers, March 2001.
[3]Crockett, A. Marrying the microand macroprudential dimensions of financial stability [C]. BIS Speeches, September 2000.
[4]Hanson, S,Kashyap, A,Stein, J. A Macroprudential approach to financial regulation [R]. Chicago Booth Research Paper, No.58, 2010.
[5]Jokipii,T,Milne,A.Bank capital buffer and risk adjustment decisions[R].Swiss National Working Paper, September 2009.
[6]Terhi, J,Alistair, M. Bank capital buffer and risk adjustment decisions [J] .Journal of Financial Stability,2010,(7) :165-178.
[7]Cordella,T, Pienknagura, S. Macro prudential policies from a micro prudential angle [R].Policy Research Working Paper, December,2013.
[8]宋琴, 郑振龙.市场结构、资本监管与银行风险承担[J]. 金融研究,2010,(11):15-21.
[9]刘胜会. 从银行业视角看宏观审慎政策的微观影响[J]. 金融论坛,2011,(10):9-16.
[10]彭建刚,王佳,邹克.宏观审慎视角下有贷期限错配流动性风险的识别与控制[J].财经理论与实践,2014,(4):2-8.
[11]彭建刚,吕志华.论我国金融业宏观审慎管理制度研究的基本框架[J].财经理论与实践,2012,(1):2-7.
[12]IMF. Macropmdential policy:an organizing framework[R].2011.
[13]Ariccia, G,Laeven,L,Marquez,R. Monetary policy, leverage, and bank risk taking [R], IMF Working Paper, December,2010.
[14]Laeven L, Levine R. Bank governance, regulation, and risk taking [J]. Journal of Financial Economics, 2009,(2):259-275.
[15]Basel Committee on Banking Supervision. Basel III:a global regulatory framework for more resilient banks and banking systems [EB/OL], www.bis.org/publ/bcbs189. pdf, 2010.
[16]Arellano M,Bond,S.Some tests of specification for panel data:monte Carlo evidence and an application to employment equations[J]. The Review of Economic Studies,1991,(58):277-297.
[17]Das, S,N.R.Sy, A. How risky are banks' risk weighted assets?evidence from the financial crisis[R]. IMF Working Paper, January 2012.
(责任编辑:宁晓青)

