基于空间矢量调制的PMSM直接转矩控制研究

王科良，朱志宇，金 贺，严 岩

（江苏科技大学 电子信息学院，江苏 镇江 212000）

永磁同步电机以其体积小、结构简单、损耗小、运行可靠，以及其具有其他电机所无法比拟的高效率、高功率因素等优点而得到人们越来越多的关注，并在工业领域已获得广泛的应用。

上世纪八十年代初期由德国鲁尔大学教授Depenbrock提出的直接转矩控制（Direct Torque Control，DTC）是继矢量控制技术之后发展起来的一种新型的具有高性能的交流调速技术。它采取定子磁链定向，直接对电机的磁链和转矩进行控制，使电机转矩响应迅速[1]。其特点为结构简单，不依赖转子参数，转矩响应迅速。自其被提出以来，已获得了极大的发展，成为了交流调速的主流。

但传统DTC由于控制周期内只有一个电压矢量，磁链和转矩不能很好地跟踪系统给定值，使永磁同步电机在运行中产生较大的脉动[2]。为了解决此问题，将空间电压矢量调制技术与DTC相结合，通过减少单个电压矢量在一个控制周期内作用的时问，及合成矢量的方法，解决电机脉动过大的问题。

1 永磁同步电机的数学模型

为了便于分析，建立电机的数学模型前作如下假设[3]：1）忽略铁心饱和、涡流和磁滞损耗；2）永磁转子没有阻尼作用；3）三相定子绕组在空间呈星形对称分布，定子各绕组的电枢电阻和电感相等；4）感应电动势及气隙磁场均按正弦分布，且不计磁场的各项谐波。

基于上述假设并运用坐标变换理论便可得到d-q同步旋转坐标系中PMSM数学模型：

1）定子电压方程：

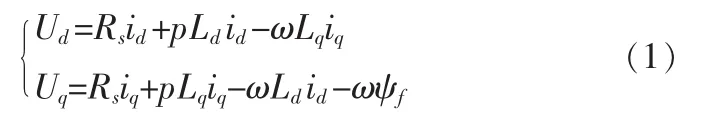
2）定子磁链方程：

3）电磁转矩方程：

其中：Ud、Uq为定子电压矢量 Us的 d、q 轴分量；id、iq为定子电流矢量is的d、q轴分量；Rs为定子绕组电阻；Ld、Lq为电机的d、q轴电感；np为电机极对数；ω为转子的电角速度；P为微分算子；Ψf为转子永磁体励磁磁链；Te为电磁转距。

2 永磁同步电机直接转矩控制

2.1 直接转矩控制

PMSM各矢量的关系如图1所示。

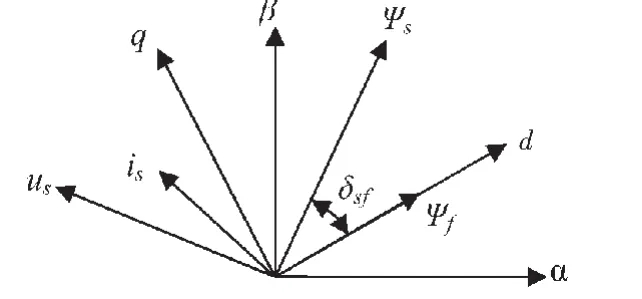
图1 矢量关系图Fig.1 Vectors relations

定子磁链在d-q轴投影分量分别如下：

式中，δsf是定子磁链 ψs与转子磁链 ψf之间的夹角，称为转矩角。

将式（4）带入式（2），可求得：

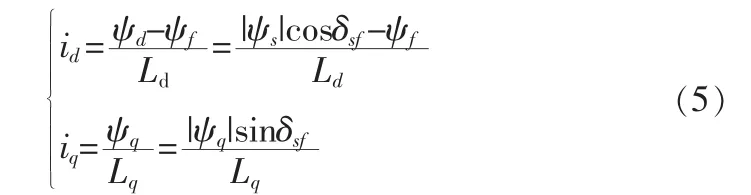
将式（5）带入式（3），可得：

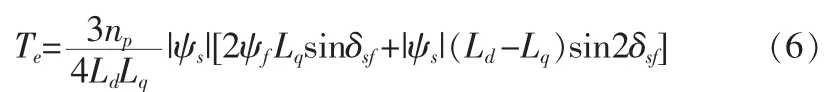
对于表面式永磁同步电机，有Ld=Lq，所以式（6）可表示为：

忽略温度对永磁材料的影响，ψs则为定值。由式（7）可知，当|ψs|保持为定值时，电动机的转矩就会随转矩角的变化而变化。考虑到PMSM的电气时间常数比转子的机械时间常数小得多，因此在瞬态时，定子磁链的旋转速度较转子磁链的旋转速度更容易改变，也就是说转矩角δsf是可以迅速调节的[4]。因此可以通过调节转矩角，达到对电动机转矩的直接控制。

2.2 定子磁链和电磁转矩控制

永磁同步电机直接转矩控制中，通常采用电压空间矢量的分析方法。三相电压型逆变器共有8种开关状态，状态描述了8个基本电压空间矢量，其中6个为幅值相等，相位互差60°的非零矢量，U1～U6，2 个为零矢量，U0、U7。 如图 2 所示。

图2 空间电压矢量扇区分布图Fig.2 Voltage vectors and zoning

在α-β坐标系下，相绕组电压方程可以表示为：

由式（8）可以得到定子磁链为：

当电动机转速不是很低时，定子电阻压降在式中所占的成分很小，可忽略不计。则：

即可以通过控制电压矢量来改变定子磁链的旋转速度，而转子磁链的旋转速度和定子电压空间矢量无直接关系，因此转子磁链的旋转速度不会发生突变。这就表明可以通过施加合适的电压空间矢量，来改变转矩角 δsf的大小，从而达到改变转矩的目的。

由式（10）可知，定子磁链矢量 ψs与电压空间矢量 Us是正交的，所以定子磁链矢量运行轨迹是沿着所施加的电压空间矢量的方向旋转的。对于每一个施加的电压空间矢量，均可沿定子磁链矢量ψs的运行轨迹方向分解为切向分量和径向分量，如图3所示，径向分量的作用直接影响定子磁链ψs的幅值，切向分量的作用直接影响定子磁链ψs的旋转方向和旋转速度。所以，可以通过选择合适的电压空间矢量来独立地控制这两个分量，也就实现了对定子磁链的电磁转矩的解耦控制[5]。

图3 基本电压空间矢量分解Fig.3 Basic voltage vectors disintegration

3 PMSM空间矢量调制直接转矩控制

3.1 空间电压矢量调制

通过选择合适的电压空间矢量来独立地控制这两个分量，也就实现了对定子磁链的电磁转矩的解耦控制，但传统的DTC中一个基本电压矢量作用整个周期，在低速时会产生脉动。

可以采用是空间电压矢量调制（SVPWM）的线性组合的控制策略，该控制策略通过合理控制两个相邻基本电压矢量及其和零矢量之间的切换，在每一个开关周期Ts内去逼近旋转参考矢量Ur，使合成电压矢量的运动轨迹逼近圆形[6]。如图2所示，以扇区Ⅰ为例，在一个采样周期内，Ur可由基本电压矢量U4、U6及零矢量U0、U7合成，通过控制逆变器输出电压矢量U4、U6及U0、U7的切换时刻，就可以逼近参考电压Ur。根据空间矢量作用等效的原则有[7]：

式中 ：T0、T4、T6、T7分别为 电压矢量 U0、U4、U6、U7的作用时间，Ts为采样周期。零矢量作用时，磁链矢量的末端始终不变。当欲合成的矢量在其它区域时，方法相同。

3.2 永磁同步电机的SVM-DTC

基于SVPWM的PMSM直接转矩控制系统结构图如图4所示。用SVM技术，通过两个相邻基本电压空间矢量和零电压矢量的线性组合与来与参考电压矢量Ur等效，能够精确补偿定子磁链和电磁转矩偏差。SVM模块之后，系统输出6路PWM，驱动电压型逆变器，实现磁链和转矩的准确、平滑控制，进而控制电机稳定运行。

采用SVM技术取代了滞环比较器和开关电压矢量选择表，改变了传统DTC在一个采样周期Ts内输出单个电压矢量的缺陷，能够在一个采样周期Ts内输出多个基本电压矢量，从而大大降低了磁链和转矩脉动，SVM技术使得逆变器开关频率也保持恒定。

4 PMSM空间矢量直接转矩控制系统仿真结果及其分析

图4 PMSM空间矢量直接转矩控制结构图Fig.4 PMSM SVM－DTC structure

根据控制的基本原理，并参照图4搭建出系统的仿真模型，如图5所示。电机参数如下：Ld=Lq=8.5 mH，Rs=1 Ω，Ψf=0.175 Wb，np=2，转动惯量 J=0.000 8 kg·m2，磁链给定为|Ψ*s|=0.66 Wb，母线电压Udc=480 V。设定仿真时间为 0.14 s，电机转速给定值为50 rad/s，在0.1 s阶跃为100 rad/s。负载转矩在0.05 s时从0 N·m 阶跃为5 N·m。

仿真结果波形如图6～图8所示。

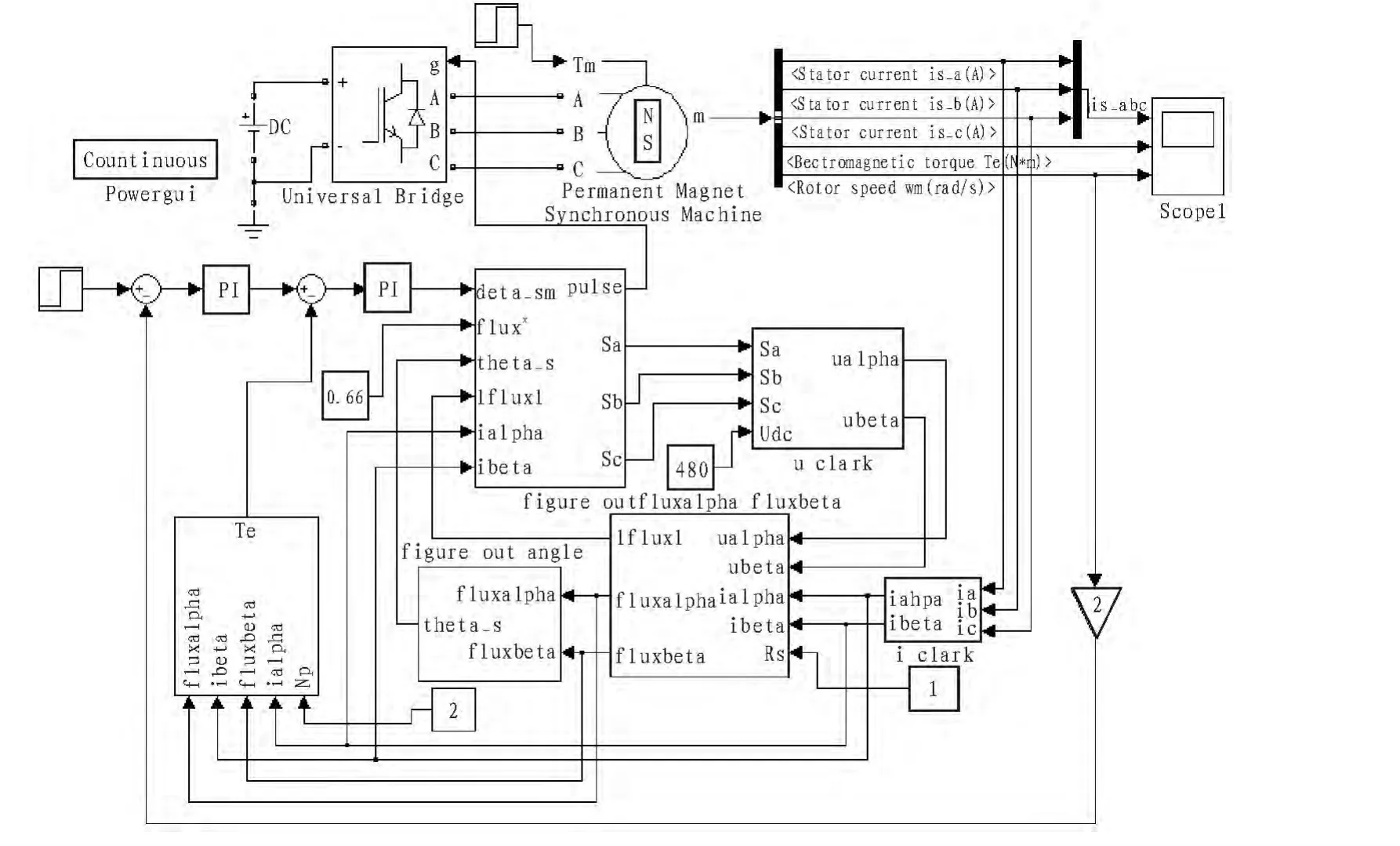
图5 系统仿真模型Fig.5 Simulation model of the system

从仿真结果图6中可以看出，磁链沿着圆形轨迹运动。从图7可以看出三相电流按正弦规律变化，说明电机的运作正常。永磁同步电动机空间矢量调制直接转矩控制系统转速响应较快，并能快速的跟随给定的变化，稳态误差也较小。

图8为电子磁链所在的扇区图，可以看出扇区号依次递增，并呈现周期性，并在电机运行速度增加一倍时，定子磁链运行一周的周期时间缩短一半。亦证明电机运作正常，定子磁链沿圆形轨迹运行。

5 结束语

本文主要对PMSM直接转矩控制原理进行分析研究，并提出了基于空间矢量调制的直接转矩控制。利用SIMULINK进行仿真，仿真结果显示此系统能很好的实现圆形磁链，转速，转矩的快速响应，较小的稳态误差，可以证明控制方案及仿真模型是正确的。将PMSM直接转矩控制不断发展完善的理论应用于生产实践，必能产生极大的社会、经济效益。

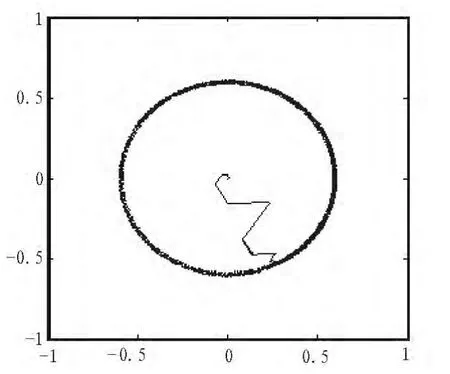
图6 定子磁链轨迹Fig.6 Flux linkage trail rout

图7 相电流及转矩、转速响应曲线Fig.7 Simulation results of phase current and torqu and rotation speed

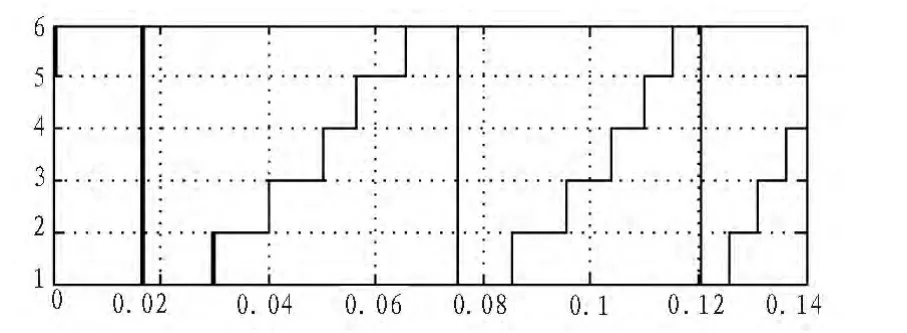
图8 定子磁链所处扇区示意图Fig.8 Sector of flux in

[1]周扬忠，胡育文.交流电动机直接转矩控制[M].北京：机械工业出版社，2009.

[2]GIUSEPPE S B，MARIAN P K.Direct torque control of PWM inverterfed AC motors-a survey[J].IEEE Transactions on Industrial Electronics，2004，51（4）:744－757.

[3]暨绵浩.永磁同步电动机及其调速系统综述和展望[J].微特电机，2007，35（3）:49－52.JI Jin-hao.Summary and outlook of PMSM and speed control system[J].Weite Motor，2007，35（3）:49－52.

[4]韩如成，潘峰，智泽英.直接转矩控制理论及应用[M].北京：电子工业出版社，2012.

[5]刘英培.PMSM直接转矩控制方法及实验研究[D].天津：天津大学，2010.

[6]陈伯时.电力拖动自动控制系统[M].北京：机械工业出版社，2006.

[7]赵洪涛.空间矢量脉宽调制方法与三相四桥臂逆变器研究[D].武汉：空军雷达学院，2005.