高中数学中知识交汇试题的处理方法
穆雪霞
石家庄市第二十三中学
高中数学中知识交汇试题的处理方法
穆雪霞
石家庄市第二十三中学
高中数学知识交汇试题的出现不仅是高中数学学科特征发展的需要,也是提高学生综合分析能力的关键。近几年的高考中,数学知识的交汇问题出现的频率越来越高。高中数学知识交汇问题出现的原因及怎样解决这类题的教学方法已经成为一线教师迫切需要解决的问题了。下面,笔者就结合多年的教学实践和经验来谈谈自己的一些想法与做法。
高中数学;知识交汇;处理方法
一、高中数学知识交汇问题出现的原因
1、学科特点发展的需要
高中数学是一门科学的、严密的自然科学知识,所以,数学学科的系统性和严密性决定了数学知识之间深刻的内在联系,它包括各部分知识的纵向联系和横向联系。所以说,高中数学知识交汇问题的出现是学科特点发展的需要。
2、高考命题发展的需要
研读《普通高等学校招生全国统一考试大纲》,不难发现:《大纲》一方面突出并强调了对主干知识以及知识和知识之间相互交汇与综合的考查,另一方面向我们昭示了“在知识网络交汇点处设计试题”,由此可见,高中数学知识交汇问题是新课程背景下必将坚持的高考命题方向。
二、走出高中数学知识交汇问题的误区
高中数学知识交汇问题其实就是把两个或几个有关的知识点结合起来,全面地考察学生能力的一种综合性试题。所以说,高中数学知识交汇问题绝对不是高中数学知识之间的机械的拼凑。
三、高中数学知识交汇问题的类型
高中数学知识交汇问题的类型有多种多样,下面,就从两个大方面来说说其类型:
1、传统知识点之间的交汇
向量与三角交汇;向量与解析几何交汇;向量与数列交汇;导数与函数、不等式交汇;导数与数列;导数与三角交汇;数列与函数交汇;数列与解析几何交汇;概率与数列交汇;立几与导数、概率交汇。
2、新增知识点的交汇
以算法为主线的交汇;以概率(几何概型)为主线的交汇;以线性规划为主线交汇。
四、高中数学中知识交汇试题的处理方法——以数列的交汇为例
数列作为一种特殊的函数,是反映自然规律的基本数学模型。新课程强调用函数的背景和研究方法来认识、研究数列,体会数列的函数背景,感受数列是研究现实问题情境的数学模型。接下来,举几个实例来阐述。
1、数列与函数的综合
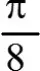
①、求证:y1+y2为定值;
③、在②的条件下,若
(n∈N*),Tn为数列{an}的前n项的和,若Tn<m(Sn+1+1)对一切
n∈N*都成立,试求实数m的取值范围。
试题分析:本例题就是一个比较典型的数列与函数交汇的问题,在解决整个问题中,用到了函数问题、数列问题、中点问题、倒数相加问题、参数分离问题等。虽然是一个题,但是涉及的知识点却是方方面面。
方法总结:数列与函数交汇问题的常见类型及解法
(1)已知函数条件,解决数列问题,此类问题一般利用函数的性质、图象研究数列问题。
(2)已知数列条件,解决函数问题,解决此类问题一般要充分利用数列的范围、分式、求和方法对式子化简变形。另外,解题时要注意数列与函数的内在联系,灵活运用函数的思想方法求解。
2、数列与不等式的综合
典型例题:(2013·宁波模拟)设公比大于零的等比数列{an}的前n项和为Sn,且a1=1,S4=5S2,数列{bn}的前n项和为Tn,满足b1= 1,Tn=n2bn,n∈N*.
(1)求数列{an},{bn}的通项公式。
(2)设cn=(Sn+1)(nbn-λ),若数列{cn}是单调递减数列,求实数λ的取值范围。
试题分析:(1)数列{an},{bn}的通项公式的求解思路:
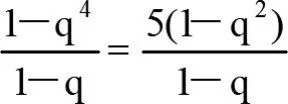
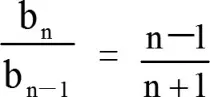
方法总结:证明与数列交汇的不等式问题的常用方法
(1)作差比较法证明。
(2)判断数列的单调性,根据数列的取值范围证明。
(3)合理利用放缩法证明。
高中数学知识交汇问题的类型有多种多样,在此只是列举数交汇的问题,选取的例题多是高考模拟试题和典型试题。解法和试题分析及规律总结有自己的观点,也有别人的成果。不足之处,望给位同仁批评指教。
[1]喻波.运用数学思想方法发展学生思维能力[J].成都教育学院学报,2001(06).
[2]陈克胜.基于数学文化的数学课程再思考[J]数学教育学报,2009(01).
穆雪霞(1981-),女,籍贯:河北省邢台市;单位:石家庄市第二十三中学。

