无粘结预应力对简支梁自振频率的试验研究
刘 森
(黑龙江省大庆地区防洪工程管理处,黑龙江 大庆 163311)
无粘结预应力对简支梁自振频率的试验研究
刘 森
(黑龙江省大庆地区防洪工程管理处,黑龙江 大庆 163311)
对4片不同形式布置的预应力筋和混凝土强度的试验梁模型进行室内试验研究,梁在不同预应力等级和竖向荷载的条件下,进行自振频率数据采集,进而找出自振频率(动刚度)与有效预应力之间的内在联系,确定预应力变化对不同预应力筋布置形式和混凝土强度等级的梁的影响效果。
有效预应力,频率,试验,无粘结预应力
0 引言
目前,在桥梁设计时,有效预应力的值仅仅是根据规范中的理论公式来估算各项预应力损失后计算的[1],同时在施工过程中,预应力的控制也仅仅停留在施工张拉技术的基础上。但在实际建设和运营中,许多因素是无法确定的,如施工误差、施工错误、混凝土收缩徐变、预应力损失等,特别是在桥梁建成后的运营过程中,由于混凝土的老化及车辆荷载的重复作用和超载等原因造成混凝土的开裂,以及在施工和设计过程中的误差等。上述原因都会使结构中实际预应力与设计值有一定的差距[2]。因此,预应力混凝土结构中有效预应力的测试评估就显得尤为必要。
国内外许多研究工作者在预应力桥梁动力特性的理论研究和试验分析等方面做了大量工作,提出了各种分析理论,也获得了大量研究数据。但是对于预应力如何影响桥梁,各方面的观点还存在较大的分歧,并未形成统一的理论。但有效预应力的存在必将与结构的某些力学参数有一定的关系,如结构动刚度(频率、阻尼)[3]。本论文的目的就是通过分析有效预应力与结构自振频率间的关系,以反映预应力钢筋的受力状态。
1 试验简介
1.1 试验梁设计
本次试验设计制作了4根结构形式相同,但预应力筋布置不同的试验梁,截面尺寸均为200 mm×200 mm,梁总长为3 100 mm,计算跨径为3 000 mm,预应力筋采用1束7Φs15.2 mm的1860级钢绞线,公称截面面积为139 mm2,锚垫板采用200(100)mm×200 mm×10 mm的Q235钢板,底部和顶部主筋分别采用2根直径为12 mm的HRB335钢筋,箍筋采用直径为8 mm的R235钢筋,设计混凝土标号采用C30和C40,4根试验梁预留管道预应力筋张拉后均不灌浆,确保预应力筋处于无粘结状态。P1梁的纵向预应力筋为通过截面形心的直线预应力筋,P2梁为存在5 cm偏心距的直线预应力筋[4],P3,P4梁为曲线配置预应力筋,P3梁采用C30混凝土,P4梁采用C40混凝土,试验梁的构造示意图如图1所示。
1.2 试验梁材料性质
为确保试验和理论计算的准确性,在进行动力试验前对材料性质进行试验,各试验材料参数见表1,表2。

表1 钢材力学指标
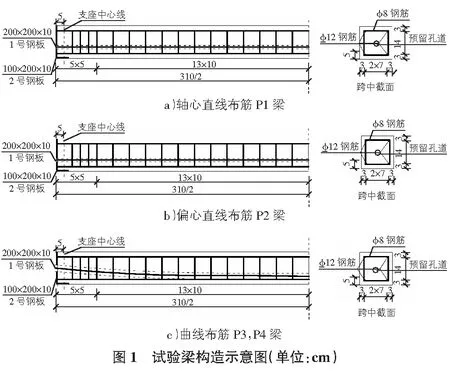
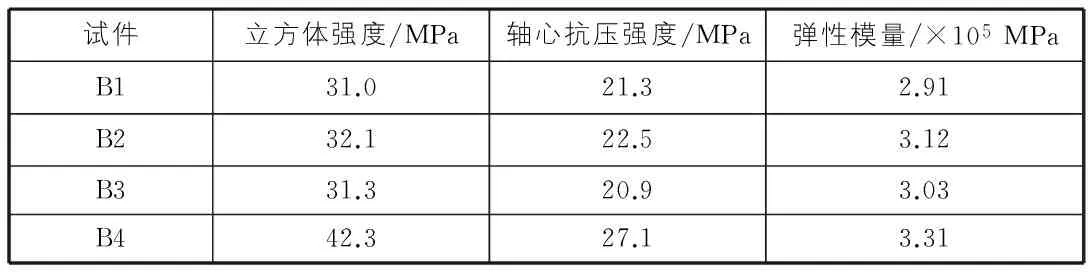
表2 混凝土力学指标
1.3 动力试验
本次试验的仪器设备有:DHDAS-5937动力测试系统、压力传感器、穿心式千斤顶、位移计、应变片、裂缝观测仪和冲击锤等。
混凝土梁中微小裂缝会对梁的动力参数产生明显的影响,因此明确预加力的大小将使梁中产生拉应力及裂缝至关重要。本文张拉控制应力的控制条件为梁不失稳、出现反拱时受拉区不产生裂缝。试验时分级张拉预应力筋,并逐级量测各试验梁的频率,经计算试验梁的最大张拉控制应力为120 kN,每级预应力筋的张拉力通过压力传感器进行控制。
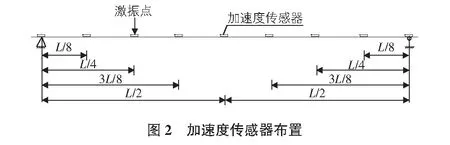
在试验梁的支点,L/8,L/4,3L/8,L/2截面以及对称截面的顶面各布设一个加速度传感器,共9个测点,如图2所示。
2 试验结果分析
记录在每级纵向荷载作用时试验梁自由振动的频率。对这四种无粘结预应力简支梁的前两阶自振频率进行计算,试验中不考虑混凝土材料的非线性特性。通过采用傅里叶变换(FFT)、频率分析,得到试验梁的频率、振型。
2.1 频率随预应力大小变化
P1~P4梁前两阶频率值与预应力值的回归方程见表3。
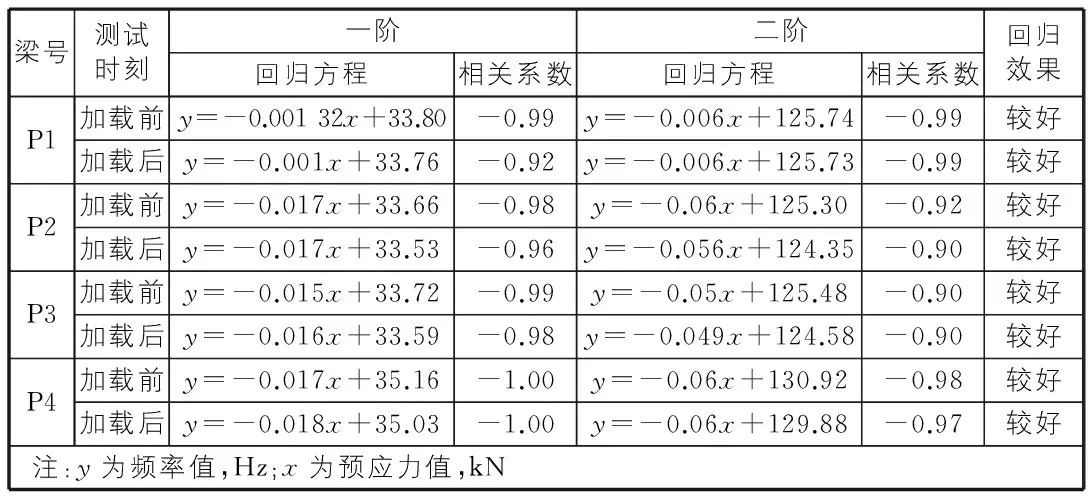
表3 P1~P4梁前两阶频率值与预应力值的回归方程
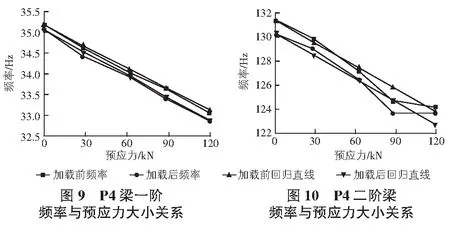
P1~P4梁频率随预应力变化曲线如图3~图10所示。

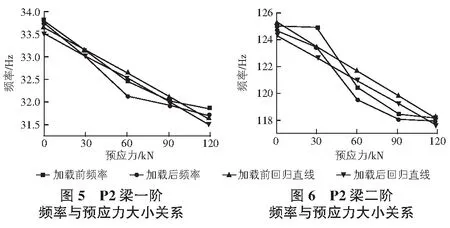
由表3的线性回归方程知试验所选4片梁(P1,P2,P3,P4)的一、二阶频率变化均与预应力变化有着较好的相关性,且效果较好。相关系数均为负数和图3~图10可以看出预应力混凝土梁的实测频率随预应力的增加而总体呈现出减小的趋势。竖向加载后的试验梁的一、二阶实测频率也随预应力的增加而减小,且加载后的一、二阶频率均不大于竖向加载前试验梁的频率。

在预应力增加至120 kN左右时:P1梁加载前一阶频率减少0.44%、二阶频率减少0.56%,加载后一阶频率减少0.29%、二阶频率减少0.56%;P2梁加载前一阶频率减少5.77%、二阶频率减少5.52%,加载后一阶频率减少6.02%、二阶频率减少5.51%;P3梁加载前一阶频率减少5.03%、二阶频率减少4.52%,加载后一阶频率减少5.48%、二阶频率减少4.97%;P4梁加载前一阶频率减少6.00%、二阶频率减少5.42%,加载后一阶频率减少6.27%、二阶频率减少4.75%。
2.2 频率随预应力筋布置变化
P1~P3梁不同预应力筋布置对梁频率影响的对比如图11,图12所示。
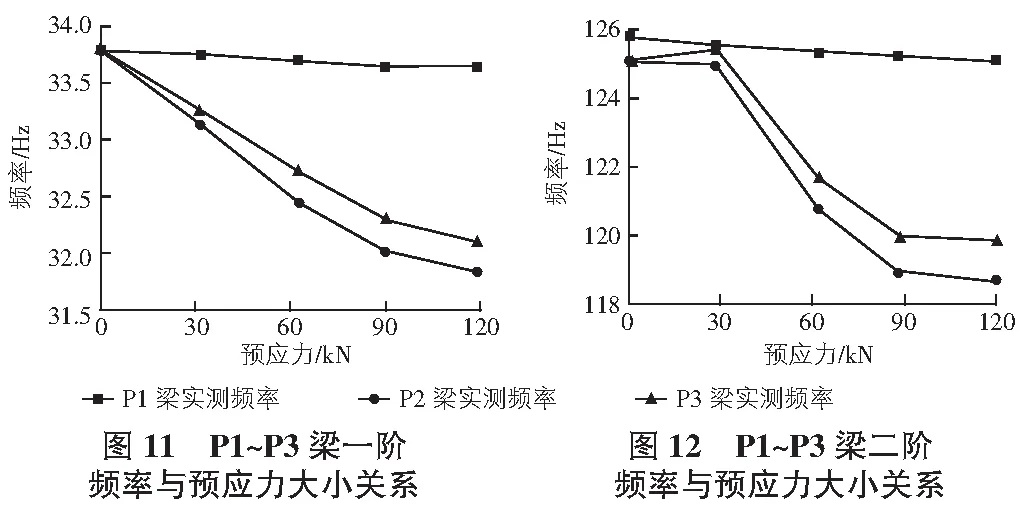
由图11,图12知,P2梁一、二阶频率变化最明显,P1梁一、二阶频率变化较小,表明预应力对通过截面形心的P1梁一、二阶频率影响要小于预应力对其余两片存在偏心距的梁(P2,P3)的影响。预应力对偏心直线预应力筋梁P2的一、二阶频率影响要大于其对偏心曲线预应力筋梁P3的一、二阶频率影响。
2.3 动刚度随预应力大小变化
根据理论计算公式计算动刚度,动刚度计算汇总表见表4。

表4 P1~P4梁动刚度计算汇总表
由表4知,P1~P4梁的动刚度均随预应力的增加而减小。在预应力筋布置形式相同,混凝土强度不同时,预应力对混凝土强度等级高的P4的动刚度影响最显著。在同等级混凝土强度的情况下,预应力对偏心直管道预应力筋的P2梁影响最大,对预应力筋通过截面形心的P1梁影响最小。
在预应力增加至120 kN左右时:P1梁动刚度减少0.83%;P2梁动刚度减少11.11%;P3梁动刚度减少9.72%;P4梁动刚度减少11.54%。
3 结语
本文通过对4片不同形式布置的预应力筋和混凝土强度的试验梁模型进行室内试验研究,得到以下结论:
1)试验梁的实测频率随预应力的增加而呈现出减小的趋势;不同预应力筋布置形式下,预应力对通过截面形心的P1梁的频率影响最小,对偏心直线预应力筋的P2梁的频率影响最大;不同混凝土强度梁的阶频率对比:P4梁的频率均高于P3梁,说明混凝土强度越高其频率越高,P4梁的频率回归曲线的斜率均大于P3梁,说明预应力对混凝土强度高的梁的频率的影响比混凝土强度低的梁显著。
2)根据频率值计算的动刚度值也随预应力的增加而减小,在预应力增加至120 kN左右时:P1梁动刚度减少0.83%;P2梁动刚度减少11.11%;P3梁动刚度减少9.72%;P4梁动刚度减少11.54%。
[1] 刘丹娜.利用钻孔法对在役桥梁进行有效预应力的估计[D].武汉:武汉理工大学,2008.
[2] 谢功元.在役混凝土梁永存预应力试验研究[D].西安:长安大学,2004.
[3] 缪 伟.预应力简支T梁有效预应力评估研究[D].西安:长安大学,2005.
[4] 张冬久,孙全胜.预应力对PC梁动静刚度影响的试验研究[J].低温建筑技术,2013(7):72-75.
Experimental research of unbounded prestressing to self-vibration frequency of the beam
Liu Sen
(DepartmentofFlood-ControlledManagementofDaqingDistrictinHeilongjiang,Daqing163311,China)
This article through to four slices of different arrangement forms of prestressed steel beam and concrete strength test beam model of indoor experimental study, the test beam under the condition of different prestress level and vertical load, collect natural frequency date of vibration, and then find out vibration frequency (dynamic stiffness) and the inner link between effective prestress, determine prestress change on different arrangement of prestressed steel beam and the influence of strength grade of concrete beam effect.
effective prestress, frequency, test, unbounded prestress
2015-01-04
刘 森(1964- ),男,高级工程师
1009-6825(2015)08-0173-03
U441.5
A

