GIS数据尺度变换中的信息熵变化

艾 廷 华，何 亚 坤,杜 欣

(武汉大学资源与环境科学学院，湖北 武汉 430079)



GIS数据尺度变换中的信息熵变化

艾 廷 华，何 亚 坤,杜 欣

(武汉大学资源与环境科学学院，湖北 武汉 430079)

基于Shannon信息熵原理的GIS数据信息量表达属于语言学信息体系中的语法层次，描述了空间目标分布结构上的不确定性特征。该文将该信息量测度方法应用于空间数据的尺度变换中，考察尺度变换中空间数据语法结构在统计意义上的变化特点，进而通过信息熵的变化发掘尺度变化中空间数据信息量的变化规律。基于空间目标群的Voronoi图剖分建立信息熵度量，以空间尺度变换中的移位、合并两种典型操作为案例，研究了面状目标群尺度变换中信息量衰减的初步规律，并尝试将其结论用于地图综合方法质量评价。

空间尺度变换;信息熵;地图综合;Voronoi图

0 引言

旨在压缩数据量、简化表达、概括主体特征的地图综合技术是空间数据处理的经典方法，是传统系列比例尺地图生产、跨尺度地图更新的技术支持。在地理信息服务新技术背景下，以海量空间数据为代表的“大数据”时代[1]需要在网络上实时传输用户感兴趣的信息内容，海量化、多元化、实时化、网络化的技术需求使得空间数据的处理、传输与分析都需要自动综合与尺度变换的支持，这对新技术背景下地图综合的研究提出了新的挑战。

顾及多种技术需求，地图综合和尺度变换首先要回答“在限定的表达空间中合理的信息量是多少？”的问题，网络实时传输的一幅地图不能包含太多的信息。为了使信息表达合理，同时自适应满足不同层次用户的要求，地图综合需要采取有效的策略度量信息量，并分析尺度变换中的信息量变化规律。地图综合领域的Töpfer法则[2]总结了尺度变换中的目标图形数量变化规律，但“数量”与“信息量”有差别，“信息量”的内涵更丰富、外延更广，如何发现尺度变换中的信息量变化规律是一个难点。

地图作为一种图形语言，具有语言学的共同特质，根据语言学层次系统将地图信息分为语法信息、语义信息和语用信息。Klir等[3]对三种信息进行了诠释，认为语法信息是事物运动的状态和方式的外在形式，语义信息是事物运动状态及其变化方式的含义，语用信息则关心事物运动状态及变化方式的效用。广泛应用的Shannon的信息熵理论是基于概率论而建立的统计信息熵[4]，属于语法层次的信息量度量，描述了空间目标分布结构上的不确定特征。Sukhov[5,6]将这一理论应用于地图信息量算，提出了符号信息熵，这种信息熵并没有考虑符号的空间分布，所以也被称为统计信息熵；随后，Neumann[7]提出了一种度量地图拓扑信息量的方法，将地图符号之间的邻接关系用对偶图表示并计算对偶图的熵，这种方法计算的熵只是表示符号类型的统计分布而不是空间分布；Bjφrke[8]设计了一种基于信息论的在道路地图中去除弧段新算法，将信息论的原理成功应用于地图综合；Li等[9]提出了基于Voronoi图的空间信息度量方法，将地图的信息量从简单的统计信息量扩展到了拓扑信息量、几何信息量和专题信息量的计算；Harrie等[10,11]提出了将地图信息的量算分为信息量和信息分布两方面进行度量。

以上研究只是对单一的静止的空间分布状态的信息描述，缺乏不同表达状态间的过程比较。按照Shannon信息熵原理[4]，信息的度量反映在信息编码、信息通道、信息解码3个环节中，由于信息通道的噪音产生信息变异，导致信息量的损失与误差产生。地图综合与尺度变换可以与信息传输过程对应，综合前的大比例尺地图为信息编码，综合后的小比例尺地图为信息解码，地图综合操作则为信息通道，通过综合操作即信息通道的有效处理，信息量压缩并产生误差信息，这一信息传输过程与地图综合的效应相一致[12]。因此，在变化过程中讨论地图信息量，更符合Shannon信息熵原理。本研究即是基于该思路将信息传输理论与制图综合过程相结合探讨尺度变化中的信息量变化规律。

1 基于Voronoi图剖分的信息熵度量

Shannon定义信息量含义为收到信息后解除的不确定度的值，解除的不确定量越大，则信息量越大。其数学表达式为：

H(X)=-∑P(ai)logP(ai) (i=1,2,…,n),∑P(ai)=1(1)

其中：P(ai)是ai事件发生的先验概率，H(X)为信息熵[13]。文中所有对数均以2为底，单位为:bit。

在地图与地理信息领域，应用Shannon信息熵原理度量信息量的关键在于空间分布概率P(ai)的定义与计算，目前定义空间目标群分布概率的形式主要有：1)数量百分比，以每种地图符号类型的数量在总的符号数量中所占的比例作为每种符号类型的概率。2)面积百分比，以每个地图符号的面积占地图总面积的百分比作为该符号的概率。数量百分比和面积百分比是Shannon信息熵原理在制图领域的直接应用。这两种信息量并没有考虑到地图符号的空间分布。从制图学的角度看，这种忽略符号空间分布来计算信息熵的方法是不合理的。Sukhov提出的符号信息熵[5,6]就属于这一类。3)类型比率，按照某种分类指标，将地图中的符号归类，以每类符号类型占地图符号总数量的比例作为该符号的概率。这种计算方法只考虑了统计意义上不同类型符号的分布，并没有很好地顾及空间分布。Neumann提出的拓扑信息熵[7]属于类型比率。4)基于Voronoi空间剖分的百分比，Voronoi图是基于邻近规则与空间竞争效应对空间目标影响区域的剖分，是空间分布分析的有力工具[14]。基于Voronoi图剖分的信息熵度量方法将符号所占有的Voronoi剖分单元(泰森多边形面积)与总的面积之比作为该符号的分布概率，不仅反映了实体对空间占有的势力划分，同时也体现出地物之间的邻接关系。

本研究即采用基于Voronoi空间剖分的百分比进行信息量量算(图1)，对于点群目标可直接构建Voronoi图；对于线群目标可采用基于道路网络连通图最短路径分析的Voronoi图空间划分方法构建道路网的Voronoi图[15]；对于面群目标可以采用基于骨架线连接得到的仿Voronoi图的剖分结构[16]。

限于篇幅本研究只讨论面目标的信息量变化规律。假设S是整个地图区域，通过建立Voronoi图，S被N个Voronoi区域Si覆盖，i=1，2，…，N，N为整个地图区域地图符号个数,则每个地图符号的概率表示如下：

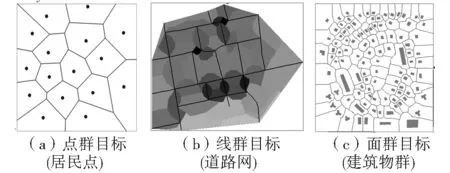
图1 三种几何实体的Voronoi图

Fig.1 Voronoi diagram of three kinds of geometric entities

(2)

(3)

(4)

由上述公式可得出影响信息熵大小的因素有：地图符号的数量和Voronoi空间分割均衡度。当比较两幅具有不同符号数量的地图时，可对式(4)做标准化处理:

HI(M)=H(M)/Hmax(M),Hmax(M)

(5)

2 面群目标移位中的信息量变化

移位是地图综合中处理各图形目标相互关系并解决空间冲突的基本方法，其目的是要保证地图各图形目标总体结构特征的适应性，即与实地的相似性。“移位”操作考察的对象是目标对或目标群。群目标的综合需顾及上下文环境的影响，既要考虑针对单个目标的综合约束，也要考虑在群结构上整体空间分布规律的保持及统计特征维护等综合约束。信息熵所衡量的是目标的空间分布结构的变化，影响信息熵大小的因素有地图符号的数量和Voronoi空间分割均衡度。单一的移位操作不改变地图符号的数量，进行移位的同时要求保证目标物的空间分布与原图一致，即Voronoi空间分割均衡度保持不变。通过以上分析得出，由于影响信息熵大小的两因素均保持不变，移位过程中信息熵需保持不变，或围绕原图信息熵上下微小波动。多组手动移位实验结果均显示，信息熵变化符合上述规律。

根据移位前后信息熵变化规律对基于场论分析的两种移位方法：单力源移位场模型[16]和多力源移位场[17]模型的移位结果进行质量评价。1)单力源移位场模型：街区块多边形边界的收缩产生了向街区块内部逐步传递并衰减的作用力，建立移位场“等距离关系曲线”，在移位场中目标的运动方向与运动距离由矢量和运算及梯度衰减函数计算完成。2)多力源移位场模型：周启等[17]提出的多力源移位场模型同时考虑外部挤压时产生的外力和通过邻近距离阈值探测空间冲突作为内力发生源引发的内力，通过计算外力与内力的矢量和得到每个空间目标最终移位的方向与偏移距离。如图2所示，从移位后的Voronoi图剖分结果看，可以明显看出图2c对应的多力源场模型移位方法在满足综合约束条件上占优，尤其在处理空间冲突和保持空间相对位置关系上。图2b中用虚线圈出了在移位过程中产生的空间冲突(A，B)及空间相对位置关系的变化(C，D)，这些问题在图2c中均得到了较好的效果。

图2 两种移位方法结果对比

Fig.2 Comparison of two displacement results

以上的定性分析多依赖于制图人员的认知，从实验效果看，多力源移位场模型能够更好地避免次生冲突。为了更直观更准确地表达移位前后空间分布的变化，本研究结合Shannon信息熵原理将空间分布的变化用信息熵作为指标来衡量，考察移位偏移量与信息熵之间的关系，研究移位过程中信息熵变化规律。考虑到移位过程中不改变地图符号的数量，采用式(2)、式(3)计算信息熵，并将实验结果呈现在表1中。

表1 实验结果

Table 1 Test results

Offse(mm)单力源移位场模型信息熵(bit)多力源移位场模型信息熵(bit)06．1434026．1434020．56．1391715．84149516．1333735．7952471．56．1296095．62900426．1326715．6830312．56．1271445．78944136．1241335．4103633．55．9899455．40926145．7131095．5379644．55．7589835．38739755．5098075．2649255．55．5695495．00711365．4893984．8772326．55．0177594．950177

对得到的实验结果进行分析，针对移位信息熵变化规律，设定两个指标(表2)：1)极差R：用以衡量信息熵波动的范围。波动范围愈小，即极差愈小愈好。2)标准差δ：用以衡量信息熵的波动率。波动率愈小，即标准差愈小愈好。

表2 实验结果比较

Table 2 Comparison of test results

方法原图信息熵(bit)最小信息熵(bit)极差R标准差δ单力源移位场模型多力源移位场模型6．1434024．8772321．26617 0．3684745．0177591．1256430．353364

两种方法所得到的信息熵均为衰减变化，并伴随微小波动，从表1的实验数据中可以看出，多力源移位场模型信息熵相邻状态间变化相对单力源移位场模型较小，信息衰减量也较小。表2 中，多力源移位场模型的极差较小，标准差也较小，说明其波动范围较小，波动性也较小，相对稳定，保证地图内容各图形目标总体结构特征与实地的相似性。实验结果与最初的认知分析结果一致，多力源移位场模型更好地保持了空间目标的分布模式。两种移位均产生了不同程度的信息熵衰减，制图综合过程总会伴随着信息量的衰减，在实际操作过程中由于街区块的压缩和衰减移位距离函数的限制使得可支配的空间总面积减少，并且Voronoi剖分面积也趋向于均衡变化，差异性减小，这些变化均会导致信息熵衰减。

3 面群目标合并中的信息量变化

多边形合并是建筑物群综合的另一个重要环节，邻近关系是合并过程的重要依据。在空间尺度变化过程中，当制图物体的图形及其间距小于可辨析距离时(面群目标为图上距离大于0.2 mm[18])，采用合并操作。多边形的合并分为多边形的邻近分析和多边形合并两种情形。群目标的综合操作要考虑群体分布所隐含的空间结构化信息，本研究采用基于最小支撑树MST的聚类方法挖掘建筑物群的分布模式(图3)，通过改变合并间距，研究合并信息量的变化规律。对图4中的街区进行合并操作，并根据式(2)、式(4)计算不同的合并间距所得到的合并信息熵。对实验数据进行最小二乘三次多项式拟合(图5)，拟合优度R2达0.9963，实验数据与拟合数据的分布基本一致。

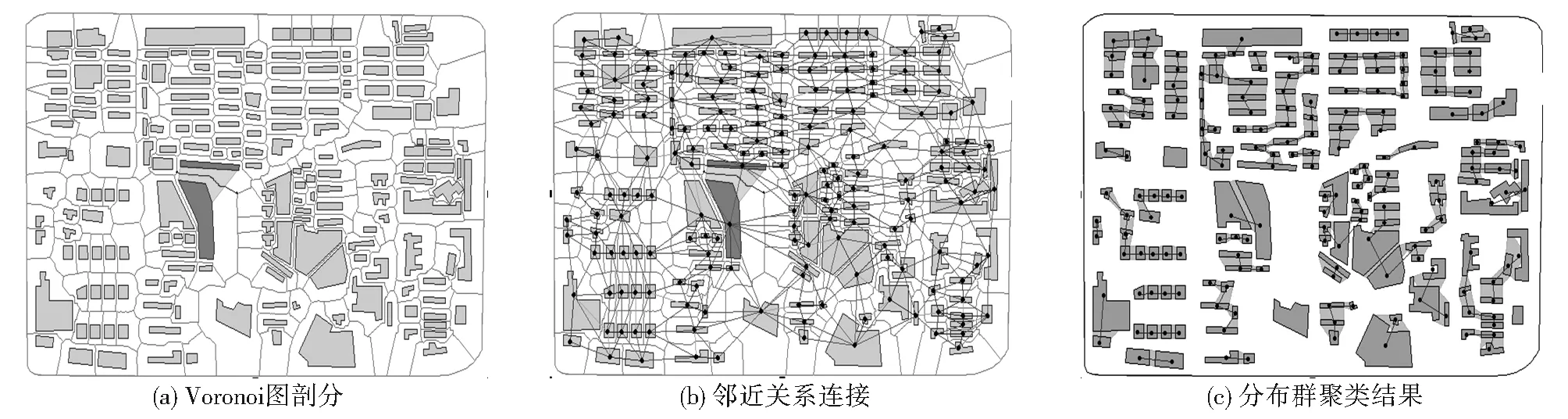
图3 基于最小支撑树MST的建筑物分布群识别

Fig.3 Building cluster recognition based on MST

图4 不同合并间距的合并结果

Fig.4 The aggregation result of different aggregation interval

图5 合并信息量的拟合曲线

Fig.5 The fitting curve of aggregation information entropy

合并操作意味着删除标志轮廓间隔的那部分数据，合并目标间的细部，使得地图目标空间占据面积增大，区域划分减少，制图物体的数量也减少，信息量减少。从实验结果拟合曲线上可以清楚地看到信息量损失速率(即拟合曲线的斜率)逐渐减小，头尾缓变，中间突变，并且有明显的拐点,呈现反“S”形曲线的特征。图5中A区和C区比较平缓，B区有明显的线性衰减的特征，在A区，由于合并间距小于0.2 mm，小于可辨析距离，地图目标的所有细节基本保留；当合并间距超过了0.2 mm，进入B区，低层次的细节均需要合并，合并信息熵受合并间距的影响逐渐增大；到达C区后，由于地图目标数量和低层次细节的减少，此时已经探测不到低层次细节的信息，曲线也趋近于平缓变化。

4 结论

本研究将信息传输理论与制图综合过程结合，并基于空间目标群的Voronoi图剖分建立语法信息熵度量。以空间尺度变换中的移位、合并两种典型操作为案例，研究了面状目标群尺度变换中信息量衰减的初步规律。移位过程中信息熵保持在原图信息熵上下微小波动，伴随移位程度的加深做缓慢衰减。合并则呈现反“S”形衰减变化的特征。以移位为例，基于信息量衰减规律对两种移位算法进行了质量评价，并得到了可行可信的结果。

本研究的实验对象均为面状目标，下一步将拓宽尺度变换操作(化简、夸大、选取)和目标对象(点目标、线目标)，总结归纳一般意义上的尺度变化导致信息量变化的规律，从而为地图综合方法质量评价提供评判依据。

[1] GOODCHILD M F,GUO H,ANNONI A,et al.Next-generation digital earth[J].Proceedings of the National Academy of Sciences,2012,109(28):11088-11094.

[2] TÖPFER F,PILLEWIZER W.The principles of selection:A means of cartographic generalization[J].The Cartographic Journal,1966,3(1):10-16.

[3] KLIR G J,FOLGER T A.Fuzzy Sets,Uncertainty,and Information[M].New York:Prentice Hall,1988.

[4] SHANNON C E.Mathematical theory of communication[J].The Bell System Technical Journal,1948,27:379-423，623-656.

[5] SUKHOV V I.Information capacity of a map entropy[J].Geodesy and Aero Photography,1967,X:212-215.

[6] SUKHOV V I.Application of information theory in generalization of map contents[J].International Yearbook of Cartography,1970,X:41-47.

[7] NEUMANN J.The topological information content of a map/an attempt at a rehabilitation of information theory in cartography[J].Cartographica:The International Journal for Geographic Information and Geovisualization,1994,31(1):26-34.

[8] BJO/RKE J T.Framework for entropy-based map evaluation[J].Cartography and Geographic Information Systems,1996,23(2):78-95.

[9] LI Z,HUANG P.Quantitative measures for spatial information of maps[J].International Journal of Geographical Information Science,2002,16(7):699-709.

[10] HARRIE L,STIGMAR H.An evaluation of measures for quantifying map information[J].ISPRS Journal of Photogrammetry and Remote Sensing,2010,65(3):266-274.

[11] STIGMAR H,HARRIE L.Evaluation of analytical methods to describe map readability[J].Cartographic Journal,2011,48(1):41-53.

[12] 艾廷华.基于空间映射观念的地图综合概念模式[J].测绘学报,2003,32(1):87-92.

[13] 钟义信.信息科学原理[M].北京:北京邮电大学出版社,1996.

[14] GOLD C M.Problems with handling spatial data-the Voronoi approach[J].CISM Journal,1991,45(1):65-80.

[15] 谢顺平，冯学智，鲁伟.基于道路网络分析的Voronoi面域图构建算法[J].测绘学报，2010,39(2)：88-94.

[16] 艾廷华.基于场论分析的建筑物群的移位[J].测绘学报，2004,33(1):89-94.

[17] 周启,艾廷华,张翔.面向多重空间冲突解决的移位场模型[J].测绘学报,2013,42(4):615-620.

[18] 祝国瑞.地图学[M].武汉：武汉大学出版社,2003.226.

Information Entropy Change in GIS Data Scale Transformation

AI Ting-hua,HE Ya-kun,DU Xin

(SchoolofResourceandEnvironmentalSciences,WuhanUniversity,Wuhan430079,China)

The information representation of GIS data belongs to the syntactic field in linguistic information system.It is based on the Shannon information theory and describes the uncertainty of spatial distributions which is related to the spatial layouts and associations.This study applies the measure of information entropy to investigate how the spatial data syntactic information changes in scale transformations and tries to detect the principles of information variation in map generalization.The entropy measure is based on the Voronoi cells of the object cluster partitioning.This study explores the law of information reduction in scale transformations by two typical generalization operators:displacement and aggregation.And this study tries to use these findings to evaluate the quality of map generalization.

spatial scale transformations;information entropy;map generalization;Voronoi diagram

2014-07-21；

2014-09-13

国家测绘地理信息局重点实验室开放基金(KLM201304)

艾廷华(1969-)，男，教授，博士生导师，研究方向为地图综合和空间认知。E-mail：tinghua_ai@tom.com

10.3969/j.issn.1672-0504.2015.02.002

P208

A

1672-0504(2015)02-0007-05