基于数据分治与双层索引的并行点面叠加分析方法研究

周 玉 科,周 成 虎，马 廷，高 锡 章，范 俊 甫，许 涛，季 民

(1.中国科学院地理科学与资源研究所，资源与环境信息系统国家重点实验室，北京 100101；2.山东理工大学建筑工程学院，山东 淄博 255049；3.山东科技大学测绘工程学院，山东 青岛 266510)



基于数据分治与双层索引的并行点面叠加分析方法研究

周 玉 科1,周 成 虎1，马 廷1，高 锡 章1，范 俊 甫2，许 涛1，季 民3

(1.中国科学院地理科学与资源研究所，资源与环境信息系统国家重点实验室，北京 100101；2.山东理工大学建筑工程学院，山东 淄博 255049；3.山东科技大学测绘工程学院，山东 青岛 266510)

地图叠加分析是一种计算密集型算法，并行化计算是加快算法执行速度的一种有效方法。该文研究分布式环境下的点面图层并行化叠加分析方法与实现。首先根据点面叠加的特点设置并行数据分解的方式，基于分治法分解空间数据，在并行系统下将地理要素分而治之。然后引入双层索引的并行叠加机制，一是对面图层根据Hilbert空间索引的排序方式分发数据，二是对点图层建立四叉树索引，对每一个进行相交运算的多边形进行快速过滤和求交。最后在Linux集群系统下实现该并行算法，其一利用MPI分布式计算环境实现在整体计算框架下的消息通讯模式的并行，其二在每个子节点中实现基于多核OpenMP工具的本地并行化。结果表明，利用双层空间索引分治的方法可实现并行数据分块，各子节点实现独立计算，减少并行系统中的I/O冲突，并行加速比明显。该方法对矢量地图运算的并行化进行了有益的尝试，为大数据时代的空间数据分析提供一种有效的途径。

地图叠加分析；并行计算；空间索引；MPI；OpenMP

0 引言

地图叠加分析(Map Overlay)是GIS空间分析中最基础、使用最频繁的一种操作[1]，指同一地域范围的两个或多个地图图层在同样空间参考系下进行叠加，获取具有新属性的空间区域并最终生成一个新的图层，图层要素属性由叠加运算符决定，其本质过程是一系列计算几何布尔操作和属性传递过程的集合。图层叠加中几何对象之间的操作已被证明为时间复杂度最少为O(nlogn)的操作[2]，因此涉及全幅地图图层的叠加分析属于计算密集型操作。点与多边形图层的叠加分析是其中基本的操作类型之一，其实质是点包含问题(单点或复杂对象组成点)。

随着数据规模的日益膨胀、实时性应用的增加，对地图叠加分析功能在计算效率、性能、处理能力等方面的要求也越来越高。并行计算技术从20世纪70年代随着计算机体系架构的进步和成熟发展起来，由于并行技术发展时间不长，因此GIS的核心空间分析功能的并行化仍然处在迅速发展时期[3,4]。近年来，并行计算机的强大硬件加速特性和新的并发设计思想为解决复杂度日益增加的地学问题和海量级别的数据处理问题提供了新的解决方案，同时也为地图叠加分析提供了理论和实践基础。点面叠加分析是地图叠加分析中的一种基本操作，输出结果判断点被多边形包含关系[5,6]。已有学者利用各种并行计算工具对地图并行叠加分析进行探索，如利用GPU加速[7]和集群并行方法[8,9]。本文利用并行计算的基础理论方法，重点研究在并行化地图叠加分析中的静态负载均衡方法，以数据并行为主线，利用Hilbert空间索引分解地理数据，达到各任务节点计算量基本平衡，各个节点再次进行细粒度并行判断包含关系。

1 双层索引方法与分治并行策略

1.1 并行叠加特征预分析

本文针对点图层与面图层的叠加分析，运算对象之间属于多对多的关系，因此研究对象的粒度应该从点与边的关系上升到点集合与多边形集合之间的关系、点集内部的空间分布特征关系和多边形集合之间的空间近邻关系。传统的并行算法设计考虑每个原子级别的操作并保证每个节点处理时间大致相同。如果按照传统设计方法将点和多边形相交降低维度将增加数据组织和计算的复杂度。假设点和多边形数量均为n，采用直接求交方法的时间复杂度为O(n2)；如果将多边形以边为粒度进行分解，假设每个多边形最少有m条边，则计算的时间复杂度会上升到O(mn2)。为更好地提升图层直接叠加效率，仍然从减少不必要耗时操作的原则出发，使用混合双层索引分解的方法对点面图层叠加进行预处理，以数据分治的方式实现并行。

图层粒度级别的多边形叠加分析更适合以面向对象的形式组织，根据并行计算的原理并行粒度越大获得的加速比越大。从点图层考察，点数据分布具有不规则性和不平衡性，因此必须加以约束减少叠加分析过程中不必要的包含测试。从GIS空间查询分析的基本过程考察(图1)，叠加分析算法可以获得并行加速的阶段主要在数据输入输出、过滤阶段和图元对象的精确几何计算过程。

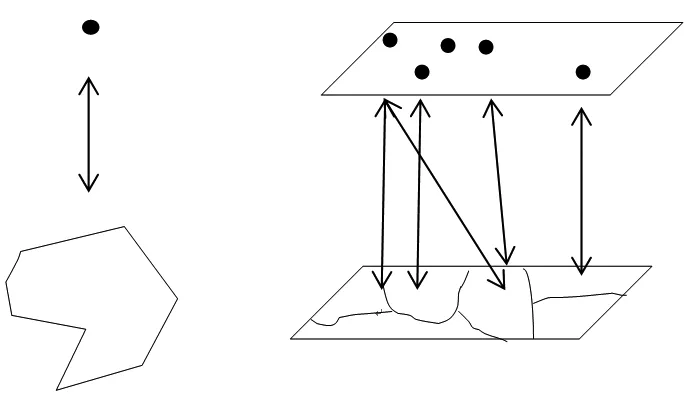
图1 单对象关系和图层多对象关系

Fig.1 Single object relationship and layer multi-object relationship

几何图形过滤阶段的加速是点面叠加分析的关键步骤[10]，图层级别的点与多边形叠加分析并行化的基础仍然是数据域分解和并发调度。本文的快速过滤是基于几何图形MBR的空间索引机制，MBR是包围图元且平行于X、Y轴的最小外接矩形在索引结构中用来代表真实几何元素。首先需要考虑叠加图层的特性，点图层的元素无外包矩形或者以计算机默认容差为宽度(长度)设定的小方格，在空间查询中小方格的相交计算明显会增加计算量。因此对于点图层采用四叉树索引的机制，其生成规则为当每个单元格只有一个点时不再继续递归划分。因为单元格是独占的，所以点图层的索引没有冗余节点。

按照二叉树表示二维点数据的方法，该研究在此基础上进行修改对点图层构建四叉树索引。点四叉树与四叉树具有同样的特点，但是当对于次分区的中心总是在一个点时，点四叉树被视为一个真树(true tree)，树的形态根据排序后的数据而定。对分布较规律的二维点的查询具有较高的效率，通常的运行时间复杂度在O(logn)之内，基于点四叉树构造空间索引的时间复杂度为O((n/2)logn)。

1.2 双层索引的多级并行方法

在并行点面叠加分析中设置主动图层和被动图层的概念。主动图层作为切割对象，被动图层作为被切割对象。因为地图系统是按照层次结构进行组织，有学者[11]已证明以点为基础要素的地图图形系统和以地图符号为基础单元的地图符号系统属于布尔代数系，因此也说明地图图层系统也可以应用于计算机处理器内的逻辑运算。虽然逻辑上两个图层叠加都是相互作用的布尔操作，容易直观地认为不存在叠加的顺序问题，但是既然涉及电子计算机的运算逻辑，其运算效率便与顺序存在一定的关系。例如，最朴素的点面图层叠加分析方法是对两个图层内的要素建立两层循环进行直接求交。从计算机内存使用和程序设计的策略衡量，对于嵌套的多层循环，外部循环量需要尽量大于内部循环量。因此在并行点面叠加的数据分解中以多边形图层作为主动图层进行包含查询。

从空间分布特点考虑，点数据图层具有聚集特性，适宜采用四叉树索引的方式。另外由于多边形数据的复杂性要高于点数据的复杂性，其空间分布不规则，根据空间数据域分解的方法，多边形图层的并行分解也需要考虑空间聚类特性，以保证各节点计算的负载均衡，因此对多边形图层建立基于Hilbert曲线排序的索引结构。首先使用MPI伪代码的形式对并行点面叠加进行描述(表1)。

表1 点面叠加的MPI伪代码

Table 1 MPI pseudo code for point-polygon overlay

1．initializeMPI2．if(masterprocess){3． buildHilbertsortindexforpolygonlayer4． broadcasttheHilbertinternalinformationtoslavenode5．}else{6． mapthenumberofpointsinfeaturelayertoanarray7． getthenumberoftotalpoints8． buildquadtreeforpoints9． calculatetheindexofpoints10． receivethespecificHilbertinternalinformationaboutpolygon11． getpolygonbetweenHilbertinternalfromlocalspatialdatabase12． Loop{13． calculatepolygoncontainpoint}14． mpi＿sendresultpointtomasternode15． }16．finalizeMPI

图层级别点面并行叠加分析的具体步骤如下：

(1)建立索引。首先数据分配采用全冗余的机制，主节点和子节点存储相同的矢量数据。主节点主要负责数据信息的一致性维护、中间结果回收。主节点对面图层分别建立基于内存的Hilbert空间索引，各子节点对所存储的点数据建立基于内存的四叉树索引。从索引结构在计算机中的存储位置可将其分为内存式和外存式两种[12]，访问计算机的内、外存储器一次所耗费的时间分别为30～40 ns和8～10 ms，因此研究采用高效的内存索引。在点面图层的并行叠加算法中空间索引有两个重要作用：一是空间数据域分解的需要，达到数据的分治和计算的负载均衡；二是几何对象进行相交判断时快速确定相交粗集，减少不必要的真实求交操作。两种方式中索引的功能都是空间查询，并且使用次数较少、周期较短，因此采用内存索引的方式能够达到快速高效的目的。

(2)多边形分配。数据处理阶段主节点对运算数据进行内存式空间索引，以多边形图层为主动查询图层，各节点进行数据本地化。有两种策略实现数据本地化，一种是分析前在每个节点预部署一份相同的数据，另一种是通过挂载共享文件系统实现数据协同访问。主节点将多边形图层按照Hilbert编码排列顺序，并将划分好的序列片段发送到各子节点。本研究采用Hilbert曲线既可以保持多边形的空间邻近性，又能够避免多边形的分配存在冗余情况(图2)。在不考虑多边形邻近性的情况下，使用多边形要素FID划分同样能够达到分治的效果，但许多地图被编辑后(删除、插入)，FID会出现不连续现象，无法保证数据分发的成功率，所以方法选择空间和数列上均连续的Hilbert曲线编码进行多边形分配。排序划分好的数组采用MPI_Send命令发送到指定子节点，各子节点接受后作为数据读取时的过滤条件只抓取部分数据。

图2 多边形索引分发方法

Fig.2 Index and distribution method of polygon

(3)索引层快速过滤。在主节点将多边形的索引标识平均分配到各子节点以后，子节点开始实际的叠加运算。首先各个节点加载本地数据，点图层作为被动图层需全部加载，同时需对其建立基于内存的四叉树索引(图3)。多边形图层按照主节点分配的标识提取图层中的部分多边形。索引层的快速过滤在多边形的MBR和点四叉树之间直接进行双层循环，快速查询与MBR相交的四叉树节点。按照叠加顺序的分析，多边形MBR作为外层循环，点四叉树作为内部循环，其中矩形间的碰撞检测如图4所示。多边形MBR首先会与高层次的树节点求交，然后依次遍历该层次下面的子节点，以发现相交的底层叶子节点为终止条件。这些叶子节点被提交，并准备做下一步的精确包含测试。

图3 中国城市四叉树索引

Fig.3 Quadtree index for cities in China

图4 MBR查询点图层四叉树示例

Fig.4 Query quadtree using MBR

图4中矩形查询的过程分为：1)查询框与Level1节点相交，但是Level1中并不包含具体点对象。2)查询框与Level2中节点相交，同样Level1中也不包含点对象，但是其子节点需要进一步检测。3)查询框与Level3中的4个索引节点相交，并且包含一个点对象，将该点追加到输出列表。右上的Level2节点没有分裂生成Level3节点，因此不必进一步查询。4)进一步查询发现查询框与6个Level4的节点相交，并在其中一个节点发现另一个点。因为刚发现的点在网格边上，所以被划归为Level3层次的点。

查询实验共探测到2个点，其中一个在Level1线上，虽然该点没有与查询框明显碰撞，但是仍然需要返回。实际运算中有大量点的情况下该判断方法作为规则执行。以上四叉树查询结果是多边形MBR所包含的点，如果不使用四叉树空间索引查询，可以利用MBR快速排斥达到同样的效果(图4)，但是查询效率相对较低。四叉树查询的计算复杂度为O(logn)，而MBR直接过滤方法的计算复杂度为O(n)，因此采用效率较高的索引查询方式。

(4)精确包含测试。在以上预处理工作的基础上，多边形MBR外的点已经被过滤掉，本阶段将进行逐步求精的工作。精确求交过程既可以直接利用典型的winding-number包含算法实现，也可以采用本文设计的多核并行方法进一步加速叠加过程。当集群中存在大规模的并行节点时，因为节点间的通讯量呈平方级别的增长，所以随着计算中间结果的通信增加带宽将成为瓶颈。一种增加程序效率线性的方法是用MPI/OpenMP混合编写并行部分。本算法设计的基本原则是MPI负责粗粒度的并行代码，OpenMP负责细粒度迭代部分的并行。设计思路是每个节点分配1～2个MPI进程后，每个MPI进程执行多个OpenMP线程。OpenMP部分由于不需要进程间通信，直接通过内存共享方式交换信息，因此可以显著减少程序所需通讯的信息。

结合以上多核算法与MPI算法，混合编程模式下的点面包含并行算法设计过程如下：1)使用初始化函数MPI_Init()启动MPI程序；2)在MPI任务内启动OpenMP并行程序；3)主进程或者MPI子进程串行执行；4)MPI的进程标记被所有OpenMP线程共享；5)串行和并行区域调用MPI库；6)使用MPI_Finize()终止MPI程序。

本文的点面图层并行叠加分析方法中MPI主要负责分发多边形要素的标记id，然后启动子节点程序载入数据并开始计算。子节点对点图层建立四叉树索引、外包矩形查询过滤过程无法并行化。最后阶段的精确包含测试可以是并行算法也可以是串行算法，将被封装成一个函数供该过程调用。单个多边形对象的并行测试方法中含有大量的同步操作和数据调度，因此为保证算法的整体稳定性，在图层级别的并行时采用串行的测试方法。

(5)结果回收和输出。子节点将真正包含测试后的结果发送给主节点，主节点负责接收并写入新图层。子节点不必发送真实的点要素数据，只需要发送包含点的fid标记数组。主节点接受后在本地图层抽取数据，减少数据的传输和消息接收的排队周期。各子节点均采用阻塞式发送，在确保主节点正确接收数据后返回消息。子节点发送中间结果说明本地计算已经完成，不需要考虑通信和计算的重叠问题，因此阻塞形式比较适合该情况。非阻塞形式的MPI通信可以实现计算与通信的重叠，但是在复杂计算中无法保证执行情况的正确反馈[13]。

2 实验与分析

2.1 多核并行实验

首先采用多核并行的方式进行实验，实验数据为全国土地利用图(图5)和POI兴趣点(表2)。图6为全国土地利用图与全国POI点并行叠加加速效果，从统计图可以看出其中并发线程间的动态调度方法加速效果明显优于静态调度方法。数据量增加引起单线程运行时间增加到6.9 s，在线程数达到8时，实际最大加速比为5.0，在一定程度上可以验证“并行数据粒度越大加速比越大”的正确性。在线程数大于4时，动态调度策略的加速比呈现明显上升趋势，说明多线程并发的点面叠加可以获得较好的加速效果。

图5 叠加多边形(土地利用分类数据)

Fig.5 Overlay polygon data

表2 叠加数据特征

Table 2 Features of overlay data

数据源名称数据类型要素数量线段数量点数量土地利用图多边形15615648894886547全国导航POI点点463142083142

图6 多核并行加速实验计算时间

Fig.6 Computing time for multi-core paralleling computing test

2.2 MPI并行实验

按照上文MPI形式的并行点面叠加算法设计，在IBM高性能集群中对该算法进行实验。实验环境为6台机架式服务器，所有机器操作系统均为Redhat6.2(Linux Kernel2.6.40)，其中一台4*6核机器作为主节点，其他节点作为子节点。空间数据存储策略为每个节点维护一个全局的矢量数据库，主节点发送主动叠加图层的分解信息，各节点独立进行主动图层(多边形)数据抽取，然后并行的对点图层实现包含测试。

MPI并行点面包含叠加实验以数据量较大的土地利用图和全国POI点为处理对象，分别采用1～12个进程测试并行加速情况。测试实验效果如图7所示，从中分析不同进程的加速情况可以看出，在计算进程不超过总体物理节点数量6时加速效果比较明显，原因是在轮询式的进程任务分配情况下每个物理节点最多只运行一个进程，不存在同节点间进程的重叠，因此对本地数据库访问和CPU的消耗都比较小。MPI单进程时计算用时为5 382 ms，在12个进程时用时为893 ms，加速比从1上升到6.0。从1个进程到2个进程时的加速效果最高，变化范围为1～1.62。从加速比的统计图可看出多机多进程情况下基本可以达到叠加的线性加速(图8)。

图7 MPI并行点面叠加实验计算耗时情况

Fig.7 Computing time for MPI test

图8 MPI并行点面叠加实验加速比情况

Fig.8 Speedup for MPI test

对比单机多核与多机器集群的并行方式可以发现，单机环境下开启多核计算得到的加速效率低于集群环境下多节点并行计算的加速效率。除单机CPU计算核心数量的限制外，OpenMP多核编程的共享内存方式对于粗粒度的并行对象读写冲突情况较多；另外重要的一点是单机环境下的数据集中式存储方式本身对并行计算的算法有较大限制，主线程启动的多个子线程无法同时在同一块物理磁盘上进行数据读写操作，导致数据并发访问成为瓶颈，而集群环境下的多节点分布式存储方式则可以有效地避免该问题，提高了执行效率(图9)。从加速效率上对比，MPI集群并行情况下的加速效率与多核并行情况下的动态负载策略基本相同，但是二者加速效率均明显高于OpenMP静态调度策略。从并行运行的时间分析，MPI并行时间少于多核并行策略，并且数据量越大加速效果越明显。

图9 MPI并行点面叠加实验加速效率

Fig.9 Speedup efficient for MPI test

3 结论

本文研究了分布式环境下点面叠加分析的在的并行化方法与实现。采用Hilbert空间索引的方式进行多边形数据的分发，各个计算节点经过快速四叉树和MBR过滤后进行点面叠加分析。双层索引以空间排序作为数据分解的依据，提高了各计算节点的运算效率(减少多边形与点的无效叠加)。分析实验结果可以得出针对点面叠加并行运算的结论：多核并行叠加和MPI集群叠加方法均可以有效地加速点面包含测试操作，不同规模和形式的处理数据应选择不同的策略：在点与面图层要素数量较大时，适宜采用MPI消息传递形式的集群并行策略，数据量较小时采用多核并行的策略，并且调度策略使用动态调度时加速效果较好。因为在数据量比较小时，MPI需要主节点进行集群环境的初始化、数据的预分解处理和分解信息分发，对于数据量较小的点面叠加这些初始化过程占用时间比例较大，只有数据量达到一定的规模集群才能够充分发挥计算功能。该方法可以实现并行计算中的数据负载均衡，减少数据冲突，并行加速效果明显，可以作为一种地学并行计算模式探讨其他空间分析方法的并行化。

[1] KRIEGEL H P,BRINKHOFF T,SCHNEIDER R.An efficient map overlay algorithm based on spatial access methods and computational geometry[C].Proc.Int.Workshop on DBMS′s for Geographical Applications,1991.

[2] DING Y,DENSHAM P J.Spatial strategies for parallel spatial modelling[J].International Journal of Geographical Information Systems,1996,10(6):669-698.

[3] 吴立新,杨宜舟,秦承志,等.面向新型硬件构架的新一代GIS基础并行算法研究[J].地理与地理信息科学,2013,29(4):1-8.

[4] 王结臣,王豹,胡玮,等.并行空间分析算法研究进展及评述[J].地理与地理信息科学,2011,27(6):1-5.

[5] 谢忠,叶梓,吴亮.简单要素模型下多边形叠置分析算法[J].地理与地理信息科学,2007,23(3):19-23.

[6] 张树清,张策,杨典华,等.简单要素模型下的多边形对象叠加并行运算策略研究[J].地理与地理信息科学,2013,29(4):43-43.

[7] 赵斯思,周成虎.GPU加速的多边形叠加分析[J].地理科学进展,2013,32(1):114-120.

[8] 范俊甫,马廷,周成虎,等.分治法在GIS多边形快速合并算法中的应用及效率提升评价模型[J].地球信息科学学报,2014,16(2):158-164.

[9] 周玉科,马廷,周成虎,等.MySQL集群与MPI的并行空间分析系统设计与实验[J].地球信息科学学报,2012,14(4):448-453.

[10] 朱效民,赵红超,方金云.鲁棒高效的矢量地图叠加分析算法[J].遥感学报,2012,16(3):448-465.

[11] 钟业勋,朱重光,魏文展.地图空间认知的数学原理[J].测绘科学,2005,30(5):11-12.

[12] 张明波,陆锋,申排伟,等.R树家族的演变和发展[J].计算机学报,2005,28(3):289-300.

[13] 胡晓力,田有先.多粒度并行计算集群研究与应用[J].电力学报,2008,22(4):436-438.

A Double-Index and Data Divide-Conquer Based Parallel Point-Polygon Overlay Method

ZHOU Yu-ke1,ZHOU Cheng-hu1,MA Ting1,GAO Xi-zhang1,FAN Jun-fu2,XU Tao1,JI Min3

(1.LREIS,InstituteofGeographicSciencesandNaturalResourcesResearch,CAS,Beijing100101; 2.SchoolofArchitecturalEngineering,ShandongUniversityofTechnology,Zibo255049; 3.CollegeofGeomatics,ShandongUniversityofScienceandTechnology,Qingdao266510,China)

Map overlay analysis is a computing intense algorithm,so it is straightforward that parallel computing algorithms can speed up the executing efficiency.The paper aims to study the method and implement of the parallel point-polygon overlay analysis in a distributed computing environment.Firstly,according to the characteristic of point-polygon overlay analysis,spatial data decomposition method is designed to make parallel available on the basis of spatial index.Then geographical data is processed by using the divide-conquer method on a parallel computing system.In this parallel point-polygon overlay method,double layer index mechanism is applied in order to accelerate the query process in geometry overlay step.On the one hand,the polygon layer is indexed and sorted by Hilbert space-filling curve,and then the data can be distributed to every computing node.On the other hand,point layer is indexed by quad-tree structure in order to speed up the query and filter process executed by every polygon.Finally,this parallel method is implemented on a Linux based cluster system.Coarse-grained task is paralleled using the MPI cluster-computing tool,and on every computing node the fine-grained task is paralleled using the OpenMP multi-core paralleling computing tool.The results show that this parallel point-polygon overlay method is able to reduce the I/O conflicts and every node is independent in computing process,from which apparent speedup is obtained.This work can give a new insight in map overlay analysis,meanwhile it provides a meaningful way for computing pattern of GIS data in the big data era.

map overlay;parallel computing;spatial index;MPI;OpenMP

2014-08-13；

2014-10-27

中国科学院重点部署项目(KZZD-EW-07)；山东科技大学科研创新团队支持计划项目(2011KYTD103)

周玉科(1984—)，男，博士后，从事高性能地学计算、空间分析研究。E-mail:zyk@lreis.ac.cn

10.3969/j.issn.1672-0504.2015.02.001

P208

A

1672-0504(2015)02-0001-06