基于多分辨率半边的三维地形自适应无缝建模

侯 绍 洋，赵 学 胜，王 鹏 飞

(中国矿业大学(北京)地球科学与测绘工程学院，北京 100083)



基于多分辨率半边的三维地形自适应无缝建模

侯 绍 洋，赵 学 胜，王 鹏 飞

(中国矿业大学(北京)地球科学与测绘工程学院，北京 100083)

“限定四叉树”法可以实现三维地形自适应无缝建模，但仍存在一些问题，如计算量大、数据冗余等。该文将多分辨率半边理论引入到三维地形建模中，提出了适合自适应地形格网存储和格网面提取的方法；设计并实现了三维地形自适应无缝建模的算法；最后，应用C语言和DirectX工具，开发了相应的可视化实验系统。与“限定四叉树”法相比，该方法不需要反复检测相邻格网的层差，且随剖分层次的增加，格网数量和渲染数据量的降低率逐渐增大，分别达13.9%和12.2%(剖分层次为7)。

自适应建模；裂缝消除；限定四叉树；多分辨率半边

0 引言

地形自适应表达对三维地形建模十分有意义，其在满足视觉要求的前提下，达到了节省内存空间、减少渲染数据量的目的[1-3]。四叉树模型是自适应表达常用的模型之一，具有结构规范、层次清晰、易于空间索引、便于纹理镶嵌等优点。但不同层次相邻格网边界处会出现裂缝，不仅影响视觉，而且从地表连续的角度而言，也是一种错误。目前，裂缝消除的方法有垂直边缘法、顶点拉伸法和“限定四叉树”法等。垂直边缘法[4，5]是在各节点边界周围生成垂直边，以遮挡裂缝，实际并未真正消除裂缝；顶点拉伸法[6，7]是对裂缝处的顶点高程进行调整，可能会导致T型节及地形失真；“限定四叉树”法[8-11]虽然克服了以上两种方法的缺陷，但是要求相邻格网的剖分层差不大于1，导致数据存在冗余，且需要反复检测相邻格网的剖分层差，计算量大。

通过分析发现，产生“裂缝”问题的根本原因是：四叉树结构将地形格网作为面的集合来存储，只对面进行管理，剖分过程操作的唯一拓扑实体是面，未涉及格网边的细分。为了从根本上解决此问题，本文拟将多分辨率半边引入到三维地形建模中，构建不产生裂缝的地形自适应建模方法。目前，多分辨率半边理论被应用于计算机图形学领域，如模型多分辨率编辑和自适应细分等[12-14]。因为该方法将物体表面抽象成具有方向的边的集合，通过边管理面，边剖分时，相应面与之同步细分，所以有望从根本上消除三维地形自适应表达中的“裂缝”现象。

1 基本理论

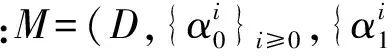
Fig.1 Adaptive partition based on multiresolution half-edges

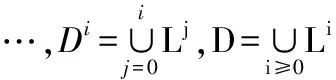
除未剖分的半边外，其余半边均被多个层次使用。因此该理论下的半边被称为多分辨率半边，可以看出相邻格网的剖分层差没有限制。

2 多分辨率半边存储原理与格网面提取方法

2.1 存储原理

如图2所示，上图表示第L层引入的两条半边he1、he2及其对合关系，反向半边指针被存储于数组0位置；下图表示第L+1层时，边被剖分，再引入两个半边he3、he4，它们作为he1、he2的反向半边存于数组1位置。即对于第j层引入的半边he，如果其最大的剖分层次为k，那么he将存储k-j+1个反向半边指针，he与第i层的关系存储于数组i-j位置。需要说明的是，多分辨率半边用于三维地形自适应建模，其后继半边指针在引入后存储内容不发生变化，所以本文不再赘述；而反向半边指针如图2所示，随着边的剖分，增加存储更高层次的反向半边指针。

图2 反向半边的存储原理

Fig.2Storageprincipleofoppositehalf-edges

2.2 格网面提取方法

多分辨率半边对格网面的管理是通过复合运算α1(α0(he))实现(图3)。假设面A内部的半边排列顺序为逆时针，提取面A的所有顶点，可以从面A的任意一个半边开始(如e1)，先对其求对合运算α0，得到反向半边e2，再对e2求排列运算α1，得到面A的下一条半边e3，反复执行α1(α0(he))，直到起始半边e1，最终得到e1e3e5e7e9e11，半边的起点集合就是面的顶点。面A此时已不再是四边形，而是由6个半边首尾相连组成的六边形，多分辨率半边结构能够自适应的管理多边形。

图3 格网面提取方法

Fig.3 Extraction method of faces

3 自适应无缝建模算法流程

如图4所示，基于多分辨率半边的三维地形自适应无缝建模算法流程分为3个阶段：第一，单层次格网建模：1)对初始格网建立半边结构，并加入节点哈希表中。2)初始格网建立后，遍历节点哈希表中上一层次剖分的节点(原节点)：如果原节点位于边界处，则直接对3个半边建立半边结构，如果节点为非边界点，那么求原节点相邻的节点(邻节点)；然后，判断邻节点是否存在：如果不存在，则对3个半边建立半边结构，如果存在，继续判断邻节点是否剖分；如未剖分，则建立3个半边的半边结构，如剖分但未建立半边结构，则建立4个半边的半边结构。3)递归执行前两步，直到完全遍历上一层次所有节点。第二，多层次格网建模：1)计算本层节点的细分准则，计算4个顶点和中心点的最大高差；2)如果超出阈值则继续剖分，将下一层节点添加到节点哈希表，标注该层节点已剖分，求得新加入节点哈希表中的节点数n，并将判断层次加1；递归执行步骤1，直到没有新的节点加入，即n=0时，建模过程结束。第三，格网面的提取及可视化：1)遍历半边哈希表，若半边没有被绘制，执行复合运算α1(α0(he))，实现单个格网面的提取，并将找到的半边标注为已绘制，直到半边哈希表结尾；2)应用DirectX对提取的面进行逐个渲染，得到无缝三维地形。

4 实验与分析

4.1 实验设计

4.2 地形简化分析

如表1所示，未简化数据是指完全四叉树剖分得到的数据，每个节点存储9个指针，包括1个父节点，4个子节点和4个顶点坐标；简化后的数据是指通过本文算法获得的数据，每个半边存储1个顶点坐标、多个反向半边和1个后继半边；简化程度是简化前后相关指标的比值。可以看出，随剖分层次增加，简化后/简化前的值越来越小；当剖分层次达到7时，存储空间和渲染三角形分别是未简化数据的33.88%和22.16%。

图4 自适应无缝建模算法流程

Fig.4 Flow chart of adaptive seamless modelling algorithm

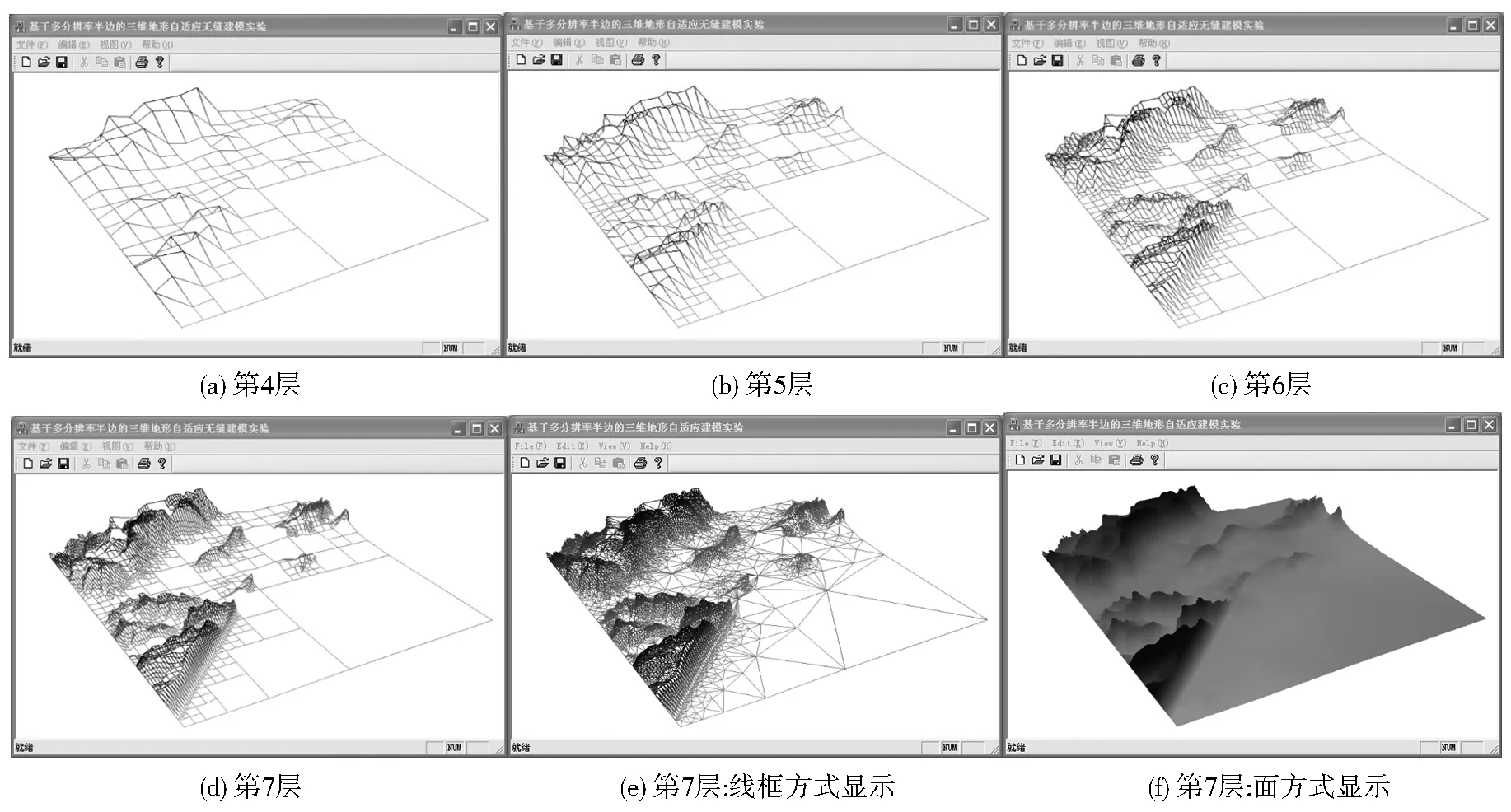
图5 基于多分辨率半边的三维地形自适应表达

Fig.5 Adaptive expression of 3D terrain based on multiresolution half-edges

4.3 地形简化对比分析

基于“限定四叉树”对同一区域、按同一简化标准进行自适应无缝建模，如图6所示，与本文图5e、图5f形成对比。从图6中可以看出，“限定四叉树”法可以消除裂缝，但需满足相邻格网剖分层差不大于1，因此导致数据冗余；且该算法需要反复检测格网间的剖分层差，导致计算量大。表2将本文算法与“限定四叉树”法进行对比，其中四边形个数、渲染三角形两个指标，随着剖分层次的提高，差距增大，当剖分到第7层时，本文算法比“限定四叉树”法分别减少13.9%和12.2%；对于每个四边形，“限定四叉树”需要存储13个指针，包括1个父节点、4个子节点、4个邻节点、4个顶点坐标，当剖分到第7层时，本文方法已略小于“限定四叉树”法。从变化趋势可以看出，剖分层次越高，本文方法优势越明显。

表1 地形简化

Table1Terrainsimplification

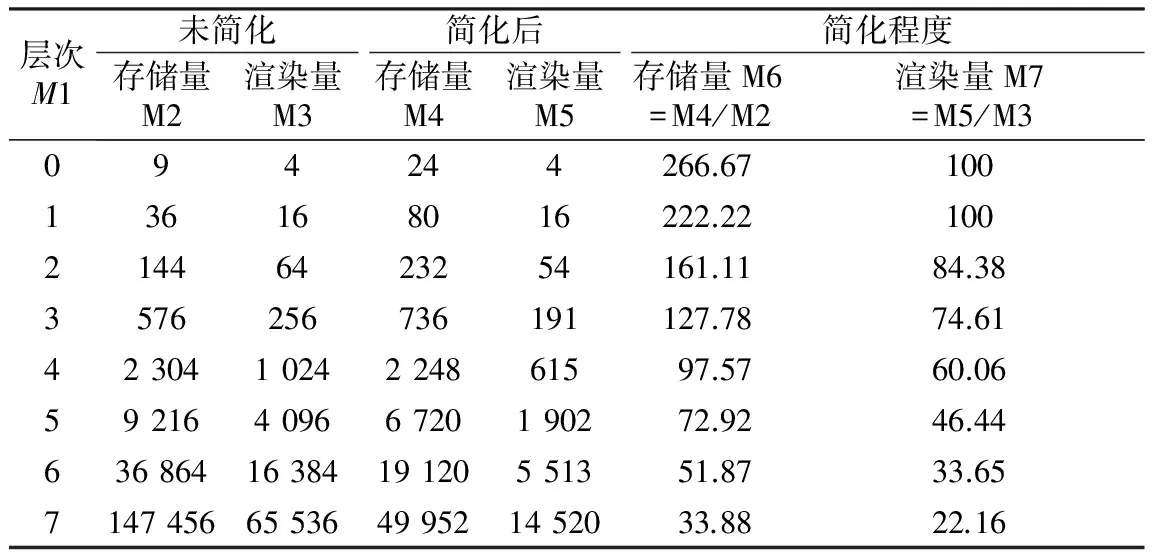
层次M1未简化简化后简化程度存储量M2渲染量M3存储量M4渲染量M5存储量M6=M4/M2渲染量M7=M5/M3094244266．67100136168016222．2210021446423254161．1184．383576256736191127．7874．61423041024224861597．5760．065921640966720190272．9246．446368641638419120551351．8733．65714745665536499521452033．8822．16

5 结论

图6 基于“限定四叉树”的三维地形自适应表达

Fig.6 Adaptive expression of 3D terrain based on "restrained quadtree"

表2 地形简化对比分析

Table 2 Contrastive analysis of terrain simplification

层次(Q1)简化后四边形的个数对比简化后需绘制的三角形个数对比简化后的存储空间对比限定四叉树(Q2)多分辨率半边(Q3)降低率M4=(Q2-Q3)/Q3∗100限定四叉树(Q5)多分辨率半边(Q6)降低率Q7=(Q5-Q6)/Q5∗100限定四叉树(Q8)多分辨率半边(Q9)降低率Q10=(Q8-Q9)/Q8∗1000110．0440．01324-84．621440．016160．05280-53．85213130．054540．0169232-37．28349466．12011915．0637736-15．5441541455．86486155．120022248-12．2954934459．7207519028．364096720-4．8561426127610．5606955139．21853819120-3．1473859332213．9165461452012．250167499520．43

为了从根本上解决三维地形不同层次相邻格网间的“裂缝”问题，本文提出基于多分辨率半边的自适应无缝表达方法。该方法不需要限制相邻格网间的剖分层差，简化后的地形数据简洁、无冗余，且不需要反复检测相邻格网的层次，计算量大幅降低。实验结果表明：本文方法能够实现三维地形自适应无缝建模，且与“限定四叉树”法相比，随剖分层次的增加，格网数量和渲染数据量的降低率逐渐增大，当剖分层次为7时，以上两个指标分别为13.9%和12.2%，优于 “限定四叉树”法。下一步研究内容包括基于多分辨率半边的三维地形数据更新方法、数据查询方法等。

[1] 孔川，罗大庸．利用动态多分辨率LOD技术的地形简化研究[J]．计算机工程与应用，2010，46(27)：156-159．

[2] 花海洋，赵怀慈．保持地形特征的网格模型简化算法[J].计算机辅助设计与图形学学报，2011，23(4)：594-599．

[3] PAJAROLA R,DECORO C.Efficient implementation of real-time view-dependent multiresolution meshing[J].Visualization and Computer Graphics,IEEE Transactions on,2004,10(3):353-368.

[4] 靳海量，高井祥．大规模地形实时可视化算法[J]．测绘科学技术学报，2006，23(1)：65-68．

[5] 胡爱华，何宗宜，马晓萍．基于LOD的大规模地形实时绘制方法[J]．测绘通报，2009(12)：23-26．

[6] 孙文彬，赵学胜．基于QTM格网的空间数据无缝层次建模[J]．中国矿业大学学报，2008，37(5)：675-679.

[7] 芮小平，张彦敏.一种实时连续LOD技术的改进算法[J].系统仿真学报，2004，16(1)：2628-2630.

[8] DENG B S,DENG T Q,YU R H,et al.Seamless rendering of large scale terrain[C].Advanced Engineering Forum，2012,6:1026-1030.

[9] 赵学胜，白建军，王志鹏.基于QTM的全球地形自适应可视化模型[J].测绘学报，2007，36(3)：316-320.

[10] 史文中，吴立新，李清泉，等.三维空间信息系统模型与算法[M].北京：电子工业出版社，2007.196-197.

[11] 王源，刘建永，江南，等.视点相关实时LOD地形模型动态构网算法[J].测绘学报，2003，32(1)：47-52.

[12] KRAEMER P,CAZIER D,BECHMANN D.Extension of half-edges for the representation of multiresolution subdivision surfaces[J].The Visual Computer,2009,25(2):149-163.

[13] KRAEMER P,CAZIER D,BECHMANN D.A general and efficient representation for multiresolution meshes:Application to Quad/triangle subdivision[C].CCCG,2007.257-260.

[14] MOUSA M H,HUSSEIN M K.Multiresolution surface representation using combinatorial maps[J].International Journal of Computers,2012,6(2):103-110.

An Adaptive Seamless Model of 3D Terrain Based on Multiresolution Half-Edges

HOU Shao-yang,ZHAO Xue-sheng,WANG Peng-fei

(CollegeofGeosciencesandSurveyEngineering,ChinaUniversityofMining&Technology(Beijing),Beijing100083,China)

Although the adaptive seamless modelling of 3D terrain can be realized based on "restricted quadtree",there are still some problems,such as abundant calculation,data redundancy,etc.The main contents are as follows.Firstly,the theory of multiresolution half-edges is introduced into the 3D terrain modelling,and a new method suitable for mesh storage and faces extraction is put forward in this paper.Then,an adaptive seamless algorithm of 3D terrain is designed and achieved.Finally,by using Clanguage and DirectX tools,an experimental system is developed.The results show that the adaptive seamless modelling of 3D terrain can be realized based on the multiresolution half-edges structure.Compared with the "restricted quadtree",this method does not need to check the level difference repeatedly between the adjacent nodes,and with the increase of partition level,reduction rate of the grid numbers and rendering data are gradually increasing,reaching 13.9% and 12.2% in 7th level.

adaptive seamless modelling;crack elimination;restrained quadtree;multiresolution half-edges

2014-07-28；

2014-09-18

国家自然科学基金面上项目“顾及多类型数据无缝融合的全球离散格网自适应建模”(41171306)；高等学校博士学科点专项科研基金项目“基于LiDAR点云的地表拓扑建模与形变分析研究”(20130023110001)

侯绍洋(1986-)，男，博士研究生，从事全球离散格网建模研究。E-mail:housaoyang@163.com

10.3969/j.issn.1672-0504.2015.02.003

P208

A

1672-0504(2015)02-0012-04