一种基于格网划分的浮动车数据自适应地图匹配方法研究

陶 华 超，马 林 兵，魏 慧 丽,周 群

(中山大学地理科学与规划学院，广东 广州 510275)



一种基于格网划分的浮动车数据自适应地图匹配方法研究

陶 华 超，马 林 兵*，魏 慧 丽,周 群

(中山大学地理科学与规划学院，广东 广州 510275)

利用单一的匹配算法对区域内的浮动车数据进行地图匹配，会出现浮动车点匹配到邻近路段上的跳跃现象。该文将区域划分格网，遍历待匹配点所在格网及其8邻域格网，筛选出候选路段、结点集合；根据候选路段、结点数量特征，自主选择合适的算法，计算几何距离和匹配度指标以评价匹配结果，确保匹配准确性。通过广州的部分区域数据进行算法验证表明：基于合适步长的格网划分能够提高匹配效率；与单一的最近点匹配算法相比，自适应综合匹配算法能够较好地避免“点跳跃”，提高匹配准确度。

浮动车数据；地图匹配；自适应；格网；匹配度

0 引言

浮动车数据(Floating Car Data ,FCD)作为一种新型的动态实时交通信息，能够承载车辆行驶过程中的瞬时速度、瞬时方位角及位置等信息。通过对这些信息的实时获取、分析，可实现对道路交通状态的实时评价，并预测未来一段时间内的交通运行状态。实际过程中由于浮动车定位精度的限制(一般为GPS单点定位)及数据采样的非连续性，会产生数据漂移现象，为了获取准确有效的道路交通信息，需利用地图匹配技术，将FCD定位到相对正确的道路位置上；因为只有判断出车辆在哪条道路上行驶，才能将FCD转化为道路的交通状态[1]。因此，地图匹配技术的优劣直接影响FCD的处理效果。

从1989年至今，至少出现了35种不同的地图匹配算法[2]，其中较为经典的有：几何分析算法[3]、拓扑分析算法[4,5]、基于概率理论[6,7]的算法及基于统计学理论[8]的改进算法等。但是实际区域内路网分布或密集或稀疏，在具体的浮动车数据匹配过程中，如果匹配算法过于单一，由于不同区域特征的差异性，会导致匹配结果在邻近路段上出现跳跃现象，如图1所示:点3匹配后落到Road2上，与其他点的匹配结果对比，存在明显 “点跳跃”现象。

本文结合待匹配FCD点的候选路段数量特征，将待匹配FCD所在的区域划分为路网密集区域、路网交叉路口、路网稀疏区域3种类型，并改进Yang等[9]提出的比值法、结点法和最短路径法3种算法，自适应地针对不同类型区域内的待匹配FCD点采用更合理的算法进行地图匹配。与文献[9]中依赖几何距离量算实现匹配不同的是，本文自适应地图匹配方法在具体实现过程中引入匹配度(方向相似性)，从几何距离和方向相似性两方面共同得出匹配结果，有效地提高了数据匹配结果的准确性。同时，本文利用格网划分法将搜索范围限定在待匹配FCD点所在格网及其8邻域格网内，改善了候选路段与候选结点的搜索效率，提高了匹配效率。

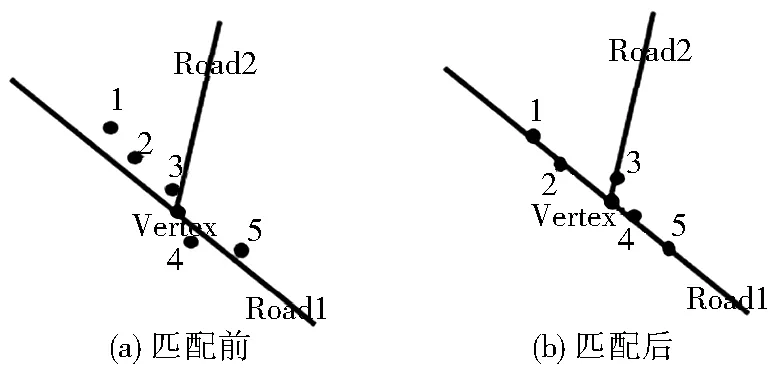
图1 匹配点跳跃

Fig.1 Jump of the matching points

1 自适应综合匹配算法

1.1 算法思想

本文在综合分析不同区域匹配特征的基础上，结合待匹配FCD点的候选路段数量特征，设计了一种自适应综合匹配算法，有效避免 “点跳跃”现象，达到区域内全面协调匹配的效果。

首先将待匹配FCD所在的区域划分为3种类型：1)路网密集区域:区域中待匹配FCD点存在多个候选路段，选择比值法能够快速有效地筛选出匹配路段;2)路网交叉路口:区域中比值法往往匹配不正确，而结点法能够通过比较待匹配FCD点与候选结点之间的距离及结点匹配度实现快速定位匹配结点；3)路网稀疏区域:对此类区域中待匹配点和以上两个区域中未能匹配的FCD点，在确定其前后都存在准确的匹配点后，运用最短路径法并结合司机出行规律及待匹配点的前后位置能够准确定位。

为了提高匹配效率，本文对区域进行格网划分，将搜索候选路段及候选结点的范围缩小为待匹配FCD点所在格网及其8邻域网格。根据研究区域的范围特征和定位精度即误差半径，将整个图幅按照合适的步长划分为M×N个单元格，通过搜索相应格网获得候选路段与结点的集合。生成的格网其覆盖范围要大小适中，确保每个格网内所包含的路段密度适宜。

为了提高匹配准确性，本文引入匹配度概念以确保FCD点与匹配道路保持最大的方向相似性。匹配度是衡量浮动车点匹配程度的一个指标，是待匹配点的瞬时方位角与待匹配点和匹配路段中邻近结点或匹配结点的方位角差值的绝对值。匹配度的计算分两种情况：1)如果是将FCD点匹配到某一路段的最近距离点，匹配度就等于待匹配点的瞬时方位角与待匹配点和匹配路段中最近距离点邻近结点的方位角差值的绝对值；2)如果是将FCD点匹配到某一路段的结点，匹配度则为该匹配点的方位角与所匹配的结点方位角差值的绝对值。其中，匹配度值越小，表明匹配度越高，反之，匹配度越低。对于匹配度计算过程中路段结点方位角的确定，可以通过路网处理预先计算出来：首先按照道路走向，将路段上的结点排序，然后根据下式计算：

(1)

(2)

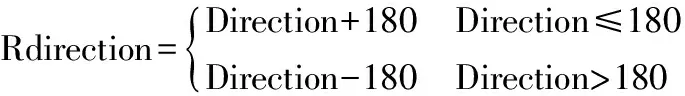
(3)

式(1)中，Startpoint、Endpoint为路段中排序前后相邻的结点。对于双向路段，结点的方位角也应有两个，而对于交叉口处结点的方位角，一般具有多个，所以关于相反方向结点方位角的表示，可以根据第一个方向排序计算的Direction结果进行式(2)中的处理，获得相反方向的Rdirection，如式(3)。

1.2 算法实现

自适应综合匹配算法是针对不同区域内FCD点综合运用比值法、结点法、最短路径法完成匹配。其中，比值法是将待匹配FCD点到候选路段集合中次近路段的距离和其到最近路段距离的比值作为一个判断指标，实际匹配过程中，如果计算得到的指标值大于指定阈值，同时该情况下计算得到的匹配度较高，待匹配FCD点就匹配到距其最近路段的最近点上，否则对该匹配点进行标记；结点法是通过计算待匹配FCD点与候选结点之间的距离及匹配度，综合比较后将其匹配到匹配度高且距离较近F的结点；最短路径法是建立在假定浮动车行驶过程中行驶者总是选择行程起止点之间最短的道路作为优先行驶路线的基础上，依据路网拓扑关系和历史数据，从候选路段中选择组成最短路径的路段，将待匹配点匹配到匹配度较高的最短路段的最近距离点。

本文方法实现主要包括路网数据处理、格网划分、自适应算法选择，具体实现流程如图2所示。首先对匹配路网进行拓扑构建及错误检查，确保路网的连通性和方向性[10]；路网结点的方位角计算可在该阶段根据处理后路段的走向，利用方位角计算公式进行。然后对区域进行格网划分，根据区域范围特征按照一定步长生成格网，并将初始FCD点、路段结点、路段与网格进行关联，通过遍历待匹配FCD点所在格网及其8邻域格网筛选出候选路段及候选结点集合。最后根据候选路段和结点的特征，分3种情况实现算法选择：对于候选路段大于等于两条的FCD点(路网密集区域)进行比值法匹配，利用匹配度进行匹配效果控制,将FCD点匹配到最近路段的最近点；对于候选路段仅有一条或未能满足比值法匹配的FCD点(通常分布于交叉口附近)，利用结点法匹配，当匹配度满足要求时将其匹配到路段结点位置；对于剩余未有效匹配的FCD点(一般为路网稀疏区域)，比值法和结点法的应用保证了前后FCD点的准确匹配，此时利用最短路径法可准确将其匹配到最短路径的最近距离点。

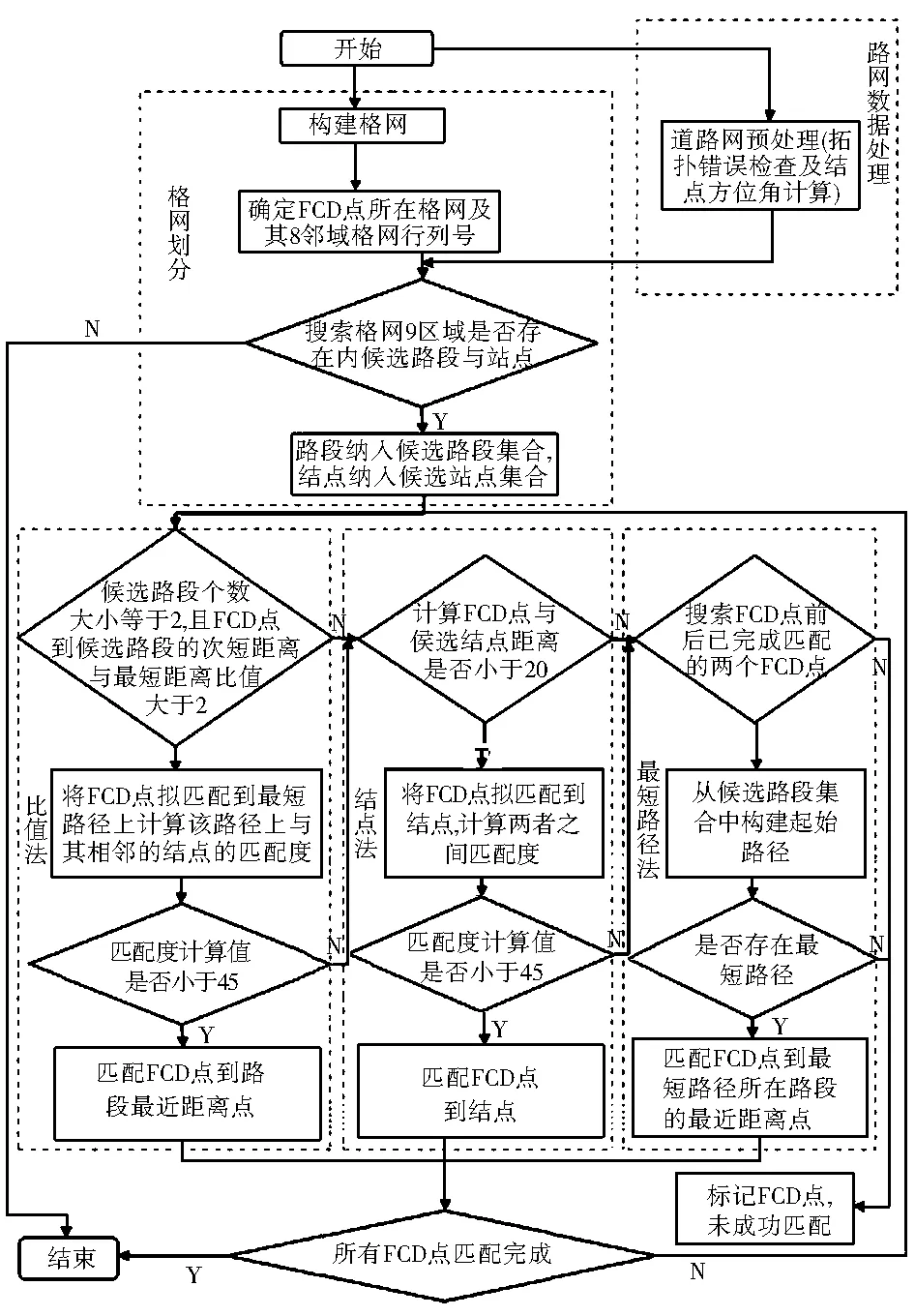
图2 本文方法技术流程

Fig.2 Flow chart of algorithm of auto-adaptive map matching for floating car data

2 算法验证

2.1 数据准备

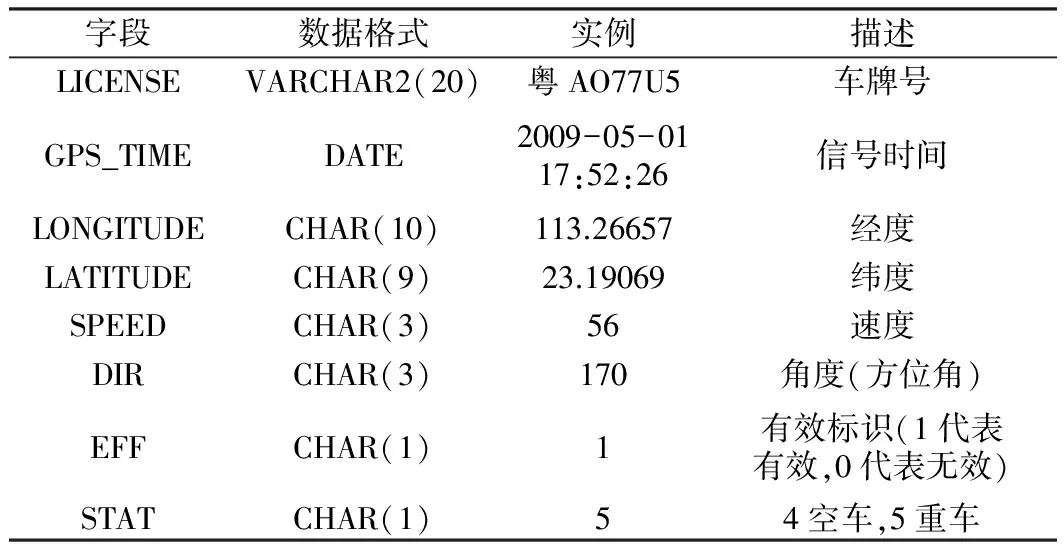
本文采用广州市越秀区与荔湾区内5辆出租车于2009年4月30日一天内采集的FCD点，其中FCD所记录的属性字段格式如表1所示。通过对FCD点进行预处理(剔除采集设备无效时获取的FCD点)后，筛选出2 147个FCD点用于对自适应综合匹配算法进行验证，检验过程中所使用的匹配道路网为越秀区与荔湾区电子地图，图3即为研究范围内的道路网及初始FCD点的分布。

表1 FCD属性字段格式

Table 1 Formats of FCD attribute field

字段数据格式实例描述LICENSEVARCHAR2(20)粤AO77U5车牌号GPS＿TIMEDATE2009-05-0117：52：26信号时间LONGITUDECHAR(10)113．26657经度LATITUDECHAR(9)23．19069纬度SPEEDCHAR(3)56速度DIRCHAR(3)170角度(方位角)EFFCHAR(1)1有效标识(1代表有效，0代表无效)STATCHAR(1)54空车，5重车

2.2 结果评价

算法实现采用C#语言编程，在3.07 GHz CPU、4 G内存的台式机上运行，2 147个FCD点匹配耗时约140 s，其中单点的平均匹配时间为65 ms。对比目前运行的大多数浮动车地图匹配算法，单点匹配时间在几毫秒至几十毫秒之间[1]，所以自适应综合匹配算法能够满足正常要求。进一步研究发现，格网步长的选择对匹配效率有较大影响；针对文中算法验证的区域(区域外接矩形为70 000 m×50 000 m，浮动车GPS设备定位误差与电子地图的精度误差都不超过20 m)，分别采用100 m、200 m、300 m、400 m、500 m、600 m、700 m的步长进行格网划分，计算得出对2 000多个FCD点进行匹配的时间变化如图4：匹配时间与格网步长呈现出“微笑曲线”。其中200～500 m的格网步长区间内地图匹配效率较高，低于或高于该区间的匹配效率有所降低，本文在验证算法有效性时以300 m作为步长，以提高匹配效率。

Fig.3 Layout of the road network and initial FCD

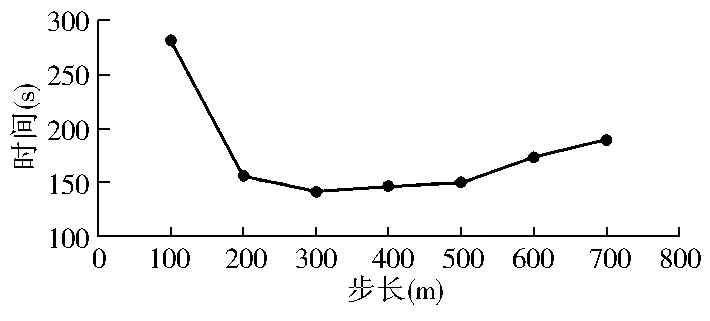
图4 格网步长对匹配效率的影响

Fig.4 Impact on matching efficiency of grid step

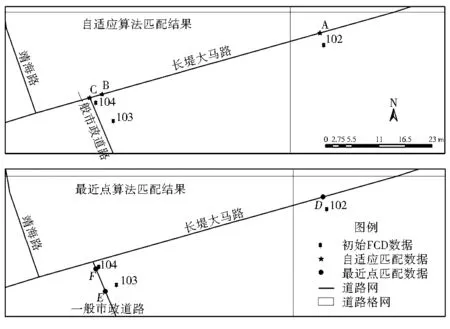
图5 自适应算法与最近点算法匹配结果对比

Fig.5 Contrast of auto-adaptive algorithm and closest point algorithm

对于FCD匹配结果的准确性，对比最近点算法(将点匹配到其最近距离路段的最近点处的一种算法)，其中车牌号“粤A04Q35”的3个FCD点匹配结果如图5所示：初始FCD点102、103、104经过自适应综合匹配算法(以下简称自适应算法)匹配相应地落在长堤大马路的A、B、C点处，对照属性表2，点104是利用自适应算法中的结点法实现匹配，点103和102是利用比值法实现匹配；而最近点算法的匹配结果显示浮动车点102落在长堤大马路的点D处，另外两点103和104则落在另外一条道路的E、F点处，具体属性信息如表3所示。通过查看初始数据的属性(表4)，3个FCD点时间间隔约为20 s，并且点102、103、104按照该时间间隔为有序FCD点，显然，自适应算法的匹配结果符合实际情况，而最近点算法匹配结果出现“点跳跃”。因此得出：在道路密集与路网交叉口区域，自适应算法的匹配结果较为准确，能够有效避免 “点跳跃”现象。

表2 自适应算法匹配后FCD属性数据

Table 2 Attribute data of FCD after matching with the auto-adaptive algorithm

IDLICENSEGPS＿TIMELONGITUDELATITUDESPEEDDIRSTATROADNAMEFLAG102粤A04Q3509：49：40113．25714223．11473482464长堤大马路1103粤A04Q3509：50：01113．25670323．11461803124长堤大马路1104粤A04Q3509：50：21113．25667823．114611133244一般市政道路2

注：“ROADNAME”属性表示FCD的匹配路段名称，“FLAG”属性表示匹配方法，其中1表示比值法，2表示结点法，3表示最短路径法。

表3 最近点算法匹配后FCD属性数据

Table 3 Attribute data of FCD after matching with the closest point algorithm

IDLICENSEGPS＿TIMELONGITUDELATITUDESPEEDDIRSTATROADNAMEFLAG102粤A04Q3509：49：40113．25714223．11473482464长堤大马路4103粤A04Q3509：50：01113．25670323．11455603124一般市政道路4104粤A04Q3509：50：21113．25668423．114598133244一般市政道路4

注：“FLAG”属性表示匹配方法，其中4表示最近点法。

表4 初始(匹配前)FCD属性数据

Table 4 Attribute data of initial (before matching) FCD

IDLICENSEGPS＿TIMELONGITUDELATITUDESPEEDDIRSTAT102粤A04Q3509：49：40113．25715023．11471082464103粤A04Q3509：50：01113．25672623．11455603124104粤A04Q3509：50：21113．25669023．114600133244

3 结语

本文在综合分析不同区域匹配特征的基础上，结合待匹配FCD点的候选路段数量特征，设计了一种基于格网划分的FCD自适应地图匹配方法。经过算法验证，利用格网划分进行候选路段和结点的初步筛选，在控制检索范围有效性上具有显著的优越性，同时合适步长的格网划分能够有效提高匹配效率；对比单一匹配算法(最近点算法)的匹配结果，本文提出的自适应综合匹配算法能够有效避免“点跳跃”，保证匹配结果的准确性。

由于文中采用的最短路径法是在一定的假设条件下执行的，最短路径的构建过程是以欧氏距离为指标，而实际出行过程中存在众多的不确定性，如司机可能会根据实际路况选择行程时间或行驶距离较为适宜的路线，那么，根据理论获得的最短路径可能并不符合司机的最短路径要求，就会产生匹配错误。因此，最短路径法需要尽可能模拟真实路况，综合差异因素寻找“出租车司机的最短路径”，这样最短路径法的匹配结果才能准确，本文算法的准确性和自适应性才更有保证，而这将是后续研究的重点。

[1] 王美玲,程林.浮动车地图匹配算法研究[J].测绘学报,2012,41(1):133-138.

[2] QUDDUS M C,OCHIENG W Y,NOLAND R B.Current map-matching algorithms for transport applications:State-of-the art and future research directions[J].Transportation Research Part C:Emerging Technologies,2007,15(5):312-328.

[3] 陆文昌,张迎,陈龙,等.基于计算几何的地图匹配算法研究[J].机械设计与制造,2012,10(1):43-45.

[4] 陈波,王茂林,王宏,等.一种基于网络拓扑关系的地图匹配算法[J].测绘科学技术学报,2006,23(5):331-334.

[5] 屈宏斌.基于网络拓扑关系的综合地图匹配算法[D].兰州:兰州大学,2006.

[6] 苏惠敏,周鹏.基于 D-S 证据理论的 GPS/MM 组合系统车辆定位算法[J].北京航空航天大学学报,2001,27(2):157-162.

[7] 杨易,谷正气,胡林,等.基于概率决策的车辆导航系统地图匹配算法[J].汽车工程,2006,28(10):897-901.

[8] WHITE C E,BERNSTEIN D,KORNHOUSER A L.Some map matching algorithms for personal navigation assistants[J].Transportation Research Part C:Emerging Technologies,2000,8(1):91-108.

[9] YANG J,KANG S,CHON K.The map matching algorithm of GPS data with relatively long polling time intervals[J].Journal of the Eastern Asia Society for Transportation Studies,2005,6:2561-2573.

[10] 朱丽云,郭继孚,温慧敏,等.一种适用于复杂城市路网的浮动车实时地图匹配技术[J].交通与计算机,2008,25(6):81-84.

Study on an Algorithm of Auto-Adaptive Map Matching for Floating Car Data Based on Grid Division

TAO Hua-chao,MA Lin-bing,WEI Hui-li,ZHOU Qun

(SchoolofGeographyandPlanning，SunYat-SenUniversity,Guangzhou510275,China)

A new method is proposed in this paper that is an auto-adaptive approach to deal with FCD to match the map based on grid.It traverses the grids including the prepared-matching point and its eight neighboring grids after the computational domain is divided into suitableM×Ngrids,and then filters out candidate sections or nodes collection.According to the quantitative characteristics of candidate sections or nodes,it is auto enough to choose the appropriate algorithm to calculate.To ensure the matching accuracy,the geometric distance and matching degree are introduced to evaluate the matching result during the implementation process.The experiment indicates that the matching efficiency will be affected by the step length of grid.And combined with matching degree,the auto-adaptive matching algorithm is better to avoid "jumps" and can increase matching accuracy comparing with the closest point matching algorithm.Discussions of the benefits and shortcomings associated with this method are provided,along with suggestion for future research.

Floating Car Data(FCD);map matching;auto-adaptive;grid;matching degree

2014-11-05；

2015-01-28

“十二五”国家科技支撑项目(37000-41070400)

陶华超(1990-)，男，硕士研究生，从事GIS理论与方法、时空数据库研究。*通讯作者 E-mail:malb@mail.sysu.edu.cn

10.3969/j.issn.1672-0504.2015.03.005

P208；U12

A

1672-0504(2015)03-0022-04