移动点与参考地物时空关系的自然语言描述方法研究
张 彩 丽,吴 静,邓 敏
(中南大学地球科学与信息物理学院,湖南 长沙 410083)
移动点与参考地物时空关系的自然语言描述方法研究
张 彩 丽,吴 静,邓 敏
(中南大学地球科学与信息物理学院,湖南 长沙 410083)
基于分解-组合的思想,首先对移动点的运动轨迹进行细化,并分别对移动点与参考地物目标的时空拓扑关系进行描述,在此基础上综合考虑它们之间的方向关系和距离关系,并对自然语言时空关系进行定义和集成描述。最后,通过实例对移动点运动轨迹进行了自然语言描述和应用分析。文中实现的移动对象运动轨迹的形式化描述方法,可广泛应用于导航系统中,对时空查询、时空分析及时空推理等诸多问题的研究具有重要意义。
移动对象;时空关系;自然语言
0 引言
移动对象是空间与时间耦合框架下的统一体,大致分为两类:位置随时间不断发生变化的移动点对象;形状随时间不断发生变化的移动面对象,其中移动点对象(如汽车、行人、飓风眼等)在交通控制、运输管理、车辆导航、移动位置服务等领域广受关注。在日常交流中,人们经常使用自然语言描述社会活动中各种空间对象之间的空间位置关系,寻找并确定相应的服务对象,因而对时空关系进行更高层次的自然语言描述可以设计更友好的人机交互界面,帮助人们快速查询,使得任何人能在任何时候、任何地点享受地理信息的服务。与静态对象的空间关系描述类似,移动对象间的时空关系可划分为时空拓扑关系、时空方向关系和时空距离关系。目前对于时空拓扑关系的研究成果较多[1-4],但与拓扑关系相比,方向关系和距离关系则更贴近人们生活、用途更为广泛,是时空数据库中数据和自然语言的一种有效连接手段[5]。
高勇等[6]将路径信息服务视为城市交通指挥系统、导航系统等信息系统中最为关键的内容,并对移动点-参考地物空间拓扑关系进行建模,将其表示为“变化前观测时刻”、“突变时刻”、“变化后观测时刻”的三元组:R=(Rts,Rtm,Rte);Naet等[7]将移动对象的运动轨迹表达为线,扩展空间线与面之间的19种拓扑关系,并用来描述足球的运动模式;Kurata等[8]用有向线表达移动点的轨迹,基于9+-intersection矩阵区分了26种有向线与面目标之间的拓扑关系。但以上3种模型均不能区分轨迹直接穿过边界或沿着边界穿出等一些细节关系,且这些模型均侧重拓扑关系的研究,而未考虑方向关系和距离关系。在采用自然语言对移动对象轨迹进行描述时,通常不是某一种类型的时空关系(如“穿过”、“进入”、“中东部”、“远离”等),而是多种类型时空关系的组合,如“穿过中东部”、“从东部边界进入”、“远离某城市”、“靠近某城郊西”等[9]。因此,单独使用时空拓扑关系、方向关系或距离关系无法描述这种复杂的自然语言时空关系。针对上述问题,本文对移动点的运动轨迹进行细化,综合考虑拓扑关系、方向关系与距离关系,并对移动点对象与参考地物的自然语言时空关系进行定义及形式化描述。
1 基于分解-组合的时空拓扑关系建模
1.1 移动点与参考地物时空拓扑关系表达
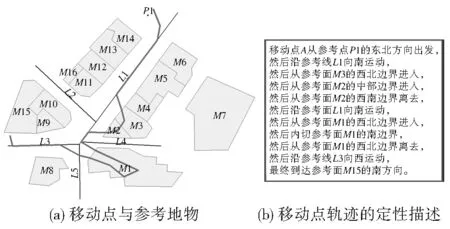
由文献[10-12]可知,复合关系可视为由多个基本关系组成,在时间段I=[t0,tn-1](∃t0,t1,…,tn-1∈I且t0 表1 移动点与参考地物的基本空间/时空拓扑关系 Table 1 The basic spatial /spatio-temporal topological relations between a moving point and a reference feature 移动点/参考点移动点/参考线移动点/参考面空间拓扑关系disjointmeetdisjointmeetdisjointmeetinside时空拓扑关系DisjointMeetDisjointMeetDisjointMeetInside 对于参考面A,移动点B特征轨迹点集和特征轨迹段集LS的建立步骤为:1)将时间段I内移动点B的起始点记为(t0,p0)并记入到特征轨迹点集PS中;2)随时间进行跟踪扫描,将移动点与参考面边界的交点分别记为(t1,p1),(t2,p2),…,(tn-2,pn-2),依次将这些交点及移动点B的终点(tn-1,pn-1)记入到PS,并将(ti,pi),(ti+1,pi+1)之间的特征轨迹段记为(Ii,fi(x,y,t)),依次记入特征轨迹段集LS;3)依次对特征轨迹段(Ii,fi(x,y,t))进行扫描判断,如果fi-1⊂∂A∧fi⊂∂A,则从PS、LS中分别去掉(ti,pi),(Ii,fi(x,y,t)),并分别将PS、LS中的下标i+1,…,m减1,直到LS中的轨迹段扫描判断完为止。对于移动点与参考点/线,将步骤2中移动点与参考面边界的交点改为移动点与参考点/线的交点。对于移动点与参考点,步骤3可省略。图1为移动点轨迹细化实例。 图1 移动点轨迹细化实例 Fig.1 A detailed illustration of moving point trajectory 记特征轨迹点(ti,pi)(0≤i≤n-1)与参考地物A的基本空间拓扑关系为top(A,ti),特征轨迹段(Ii,fi(x,y,t))(0≤i≤n-2)与参考地物A的基本时空拓扑关系为top(A,Ii),则时间段I内移动点B与参考地物A的时空拓扑关系可以表达为时间段I内移动点B轨迹细化片段与参考地物A拓扑关系的集成:Top(A,B,I)=(top(A,t0),top(A,I0),…,top(A,tn-2),top(A,In-2),top(A,tn-1))。 1.2 移动点与参考地物的复合时空拓扑关系定义 理论上,时间段I内移动点与参考地物的时空拓扑关系有许多种,基于上述方法本文给出了一些常见复合时空拓扑关系的定义,根据移动点与参考点、线、面定义的相同与不同列于表2。为便于区分,这里用P表示移动点,p、l、r分别表示参考点、线、面。其中“→”表示拓扑关系发生变化的先后顺序,“←”表示某时空拓扑关系的逆。 表2 移动点与参考点、线、面复合时空拓扑关系定义 Table 2 Definitions of composite spatio-temporal topological relationships between a moving point and a reference point (or a reference line or a reference region) 定义1P(p,l,r)≡-Arrival≡disjoint→Disjoint→meet定义2Pr⁃Enter≡disjoint→Disjoint→meet/Meet→Inside定义3P(p,l)⁃Leave≡P(p,l)⁃Arrival←Pr⁃Leave≡Pr⁃Enter←定义4Pr⁃Go⁃away⁃from≡Pr⁃Arrival←定义5Pp⁃Cross≡Pp⁃Arrival→Pp⁃Leave Pr⁃Cross≡Pr⁃Enter→Pr⁃Leave定义6Pp⁃Return≡meet→Disjoint→meet定义7Pr⁃In⁃touch≡Inside→meet→Inside定义8Pr⁃Out⁃touch≡disjoint→Disjoint→meet→Disjoint→disjoint定义9Pr⁃Bypass≡disjoint→Disjoint→Meet→Disjoint→disjoint 根据以上思想,图1a、图1c中时间段I内移动点B与参考地物A的时空拓扑关系分别表达为:Top(A,B,I)=(disjoint,Disjoint,meet,Disjoint,disjoint)、(disjoint,Disjoint,meet),相应的复合关系为:Pp-Cross、Pr-Arrival。 由空间认知可知拓扑关系是实现各类空间信息集成描述的基础,而方向关系和距离关系是对空间目标相对位置关系的进一步约束。因此需根据不同类型的参考地物,在时空拓扑关系的基础上描述局部方向关系和距离关系。 2.1 集成方向的复杂时空关系定义及描述 2.1.1 移动点/参考点 移动点与参考点方向关系的自然语言描述大多只考虑起始及终止特征轨迹点,考虑到投影模型不能提供人们常用的东南西北的方位关系,Frank通过比较得出基于锥体模型在方向描述上较优的结论,本文采用8方向锥形模型判断起始与终止特征轨迹点与参考点的方向关系。 定义1Pp-Start-d(A,B)≡(top(A,t0)=disjoint)∧dir(A,t0),其中d∈(N,S,W,E,NW,NE,SW,SE)⟹移动点B从参考点A的d方向出发。 定义2Pp-End-d(A,B)≡(top(A,t0)=disjoint)∧dir(A,tn-1),其中d∈(N,S,W,E,NW,NE,SW,SE)⟹移动点B到达参考点A的d方向。 2.1.2 移动点/参考线 移动点与参考线方向关系的描述大多只考虑起始特征轨迹点及与参考线时空拓扑关系为Meet的特征轨迹段,考虑到对于线参考地物(河流、道路)通常不会使用所有绝对方向谓词(例如,汽车沿着湘江从南往北行驶,在某时刻该汽车位于湘江东或湘江西;或者汽车沿着五一大道从西往东行驶,在某时刻位于五一大道东或西),本文采用文献[14]的方法根据参考线的走向对空间方向关系进行划分。 定义1Pl-Start-d(A,B)≡(top(A,t0)=disjoint)∧dir(A,t0),其中d∈(N,S,W,E)⟹移动点B从参考线A的d方向出发。 定义2Pl-End-d(A,B)≡(top(A,tn-1)=disjoint)∧dir(A,tn-1),其中d∈(N,S,W,E)⟹移动点B到达参考线A的d方向。 定义3Pl-Along-d(A,B)≡(top(A,Ii)=Meet)∧(dir(ti,ti+1)=d),其中特征点间方向关系采用四方向锥形模型,d∈(N,S,W,E,O)⟹移动点B沿着参考线A向d运动。 2.1.3 移动点/参考面 对于参考面,方向关系的描述需同时考虑特征轨迹点和特征轨迹段,其方向关系可以根据杜世宏等[10]提出的细节方向关系模型进行判断。 定义1Pr-Start-d(A,B)≡(top(A,t0)=disjoint)∧dir(A,t0),其中d∈(N,S,W,E,NW,NE,SW,SE,O)⟹移动点B从参考面A的d方向出发。 定义2Pr-Start-d(A,B)≡(top(A,t0)=(top(A,t0)=inside)∧dir(A,t0),其中d∈(NP,SP,WP,EP,NWP,NEP,SWP,SEP,O)⟹移动点B从参考面A的d部出发。 定义3Pr-Start-d(A,B)≡(top(A,t0)=meet)∧dir(A,t0),其中d∈(NL,SL,WL,EL,NWL,NEL,SWL,SEL,O)⟹移动点B从参考面A的d边界出发。 定义4Pr-End-d(A,B)≡(top(A,t0)=disjoint)∧dir(A,t0),其中d∈(N,S,W,E,NW,NE,SW,SE,O)⟹移动点B到达参考面A的d方向。 定义5Pr-End-d(A,B)≡(top(A,t0)=inside)∧dir(A,t0),其中d∈(NP,SP,WP,EP,NWP,NEP,SWP,SEP,O)⟹移动点B到达参考面A的d部。 定义6Pr-End-d(A,B)≡(top(A,t0)=meet)∧dir(A,t0),其中d∈(NL,SL,WL,EL,NWL,NEL,SWL,SEL,O)⟹移动点B达到参考面A的d边界。 定义7Pr-Enter_d(A,B)≡(top(A,Ii)=Disjoint)∧(top(A,Ii+1)=Inside)∧(dir(A,ti+1)=d)或(top(A,Ii)=Meet)∧(top(A,II+i)=Inside)∧(dir(A,ti+1)=d),其中d∈(NL,NWL,WL,SWL,SL,SEL,EL,NEL)⟹移动点B从参考面A的d边界进入。 定义8Pr-Leave_d(A,B)≡(top(A,Ii)=Inside)∧(top(A,Ii+1)=Disjoint)∧(dir(A,ti+1)=d)或(top(A,Ii)=Meet)∧(top=(A,Ii+1)=Disjoint)∧(dir(A,ti+1)=d),其中d∈(NL,NWL,WL,SWL,SL,SEL,EL,NEL)⟹移动点B从参考面A的d边界离去。 定义9Pr-In-touch_d(A,B)≡(top(A,Ii)=Inside)∧(top(A,Ii+1)=Inside)∧(dir(A,ti+1)=d),其中d∈(NL,NWL,WL,SWL,SL,SEL,EL,NEL)⟹移动点B内切参考面A的d边界。 定义10Pr-Out-touch_d(A,B)≡(top=Disjoint)∧(top(A,Ii+1)=Disjoint)∧(dir(A,ti+1)=d),其中d∈(NL,NWL,WL,SWL,SL,SEL,EL,NEL)⟹移动点B外切参考面A的d边界。 定义11Pr-Alongside_d(A,B)≡(top(A,Ii)=Meet)∧(dir(A,Ii)=d),其中d为8方向边界方向关系NL,NWL,WL,SWL,SL,SEL,EL,NEL或4方向边界方向关系NL4,SL4,EL4,WL4⟹移动点B沿着参考面A的d边界运动。 定义12Pr-Cross-d(A,B)≡(top(A,I)=Cross)∧(top(A,Ii)=Inside)∧(dir(A,Ii)=d),其中d∈面目标A内部的复合方向(NP4,WP4,SP4,EP4,CPNS,CPEW,CPSW-NE,CPNW-SE,CP)⟹移动点B穿过参考面A的d部。 2.2 集成距离的复杂时空关系定义及描述 移动点与参考地物的时空距离关系与特征轨迹段中移动轨迹点与参考地物的距离有关,于是,根据特征轨迹段与参考地物的时空拓扑关系可得相应的描述规则。 特征轨迹段与参考地物的时空拓扑关系为3种:Disjoint、Inside、Meet,而特征轨迹段与参考地物时空拓扑关系为Meet时,这一轨迹段内移动轨迹点与参考地物的距离均为0,故不考虑距离也能描述移动点沿着参考地物运动,本文集成Disjoint、Inside这两种时空拓扑关系与距离关系对移动点与参考地物的复杂时空关系进行定义(图2)。 对于参考地物为面的情况,定义d(∂A,ti)为轨迹点pi到参考面A边界的最小距离,dmin(∂A,Ii)为特征轨迹段li中各轨迹点到参考面A边界最小距离的最小距离,dmax(∂A,Ii)为特征轨迹段li中各轨迹点到参考面A边界最小距离的最大距离,d(∂A,ti+1)为轨迹点pi+1到参考面A边界的最小距离。 (1)特征轨迹段与参考面相离(Disjoint)。 定义1Pr-OutApproach≡d(∂A,ti)>=dmax(∂A,Ii)>dmin(∂A,Ii)>=d(∂A,ti+1)⟹移动点B逐步靠近参考面A。 定义2Pr-OutGo-away-from≡d(∂A,ti)<=dmin(∂A,Ii) 定义3Pr-OutAround≡d(∂A,ti)≈dmin(∂A,Ii)≈dmax(∂A,Ii)≈d(∂A,ti+1)⟹移动点B围着参考面A运动。 定义4Pr-OutApproach-Away≡d(∂A,ti)>dmin(∂A,Ii) 定义5Pr-OutAway-Approach≡d(∂A,ti) (2)特征轨迹段被参考面包含(Inside)。 定义6Pr-InApproach≡d(∂A,ti)>=dmax(∂A,Ii)>dmin(∂A,Ii)>=d(∂A,ti+1)⟹移动点B逐步靠近参考面A内部边界。 定义7Pr-InGo-away-from≡d(∂A,ti)<=dmin(∂A,Ii) 定义8Pr-InAround≡d(∂A,ti)≈dmin(∂A,Ii)≈dmax(∂A,Ii)≈d(∂A,ti+1)⟹移动点B围着参考面A内部运动。 定义9Pr-InApproach-Away≡d(∂A,ti)>dmin(∂A,Ii) 定义10Pr-InAway-Approach≡d(∂A,ti) 图2 移动点与面目标时空距离关系实例 Fig.2 An example of spatio-temporal distance relationships between a moving point and a reference region 当参考地物为点/线时,特征轨迹段与其时空拓扑关系为Disjoint,时空距离关系的定义与移动点/面的第一种情况相同。其中,d(∂A,ti)为轨迹点pi到参考点/线A的最小距离,dmin(∂A,Ii)为特征轨迹段li中各轨迹点到参考点/线A最小距离的最小距离,dmax(∂A,Ii)为特征轨迹段li中轨迹点到参考点/线A最小距离的最大距离,d(∂A,ti+1)为轨迹点pi+1到参考点/线A的最小距离。 根据以上集成方向和距离的复杂时空关系定义,图1b可以描述为:移动点B从参考线A的北方向出发,逐步靠近参考线A,沿着参考线A向东运动,逐步远离参考线A,最终到达参考线A南方向。 根据上述集成方向的复杂时空关系描述方法,基于Microsoft公司的Visual Studio 2008平台,采用C#编程语言,使用ESRI公司的ArcEngine组件库,对图3a中移动点的轨迹进行描述,如图3b。 根据本文提出的思想在实际应用中可以根据移动用户请求,进行出行规划生成最优路径,最后对该路径用自然语言进行描述,实现图文转换,并将结果通过移动通讯网络对移动用户提供服务。如果在导航应用中需要对行驶距离进行定性描述,可以根据上述集成距离的复杂时空关系描述方法进行描述;如果需要对行驶距离进行定量描述,只需对特征轨迹段长度进行计算即可。 图3 实验分析 Fig.3 A test for moving point trajectory 不仅如此,根据上述定义还可以对移动轨迹进行快速的定位查询,这不仅可以应用于LBS、军事领域,还有助于正确掌握台风、气旋等各种风暴所造成的灾害方位,进行快速救灾处理。时空数据库的查询语言为STQL,可进行一些复杂时空分析操作,设有模式如下: Countries(id:integer,name:string,geometry:region) Planes(id:integer,name:string,route:mpoint) 查询1 查询在我方领空西北边界逗留的敌机 SELECT p.name FROM Planes,Countries WHERE Countries.name="China" ANDAlongside_NWL(Countries.geometry,p.route) 查询2 查询逐步靠近我方领空的敌机 SELECT p.name FROM Planes,Countries WHERE Countries.name="China" ANDPr-OutApproach(Countries.geometry,p.route) 本文根据移动点对象的特性,基于分解-组合的思想对移动点与参考目标的时空拓扑关系进行表达。该方法不仅解决了现有模型存在的移动点轨迹内部与参考地物相交的一些细节关系区分问题,而且综合考虑方向、距离关系对复杂自然语言时空关系进行了定义及描述,对时空查询及推理具有一定的研究意义。本文移动对象运动轨迹的形式化描述方法可广泛应用于导航系统中,下一步将结合时空推理的方法,对移动对象的运动轨迹进行预测。 [1] 高勇,张晶,朱晓禧,等.移动对象时空拓扑关系模型[J].北京大学学报(自然科学版),2007,43(4):468-473. [2] CLARAMUNT C,BIN J.An integrated representation of spatial and temporal relationships between evolving regions[J].Geographical Systems,2001,3(4):411-428. [3] HALLOT P,BILLEN R.Spatio-temporal configurations of dynamics points in a 1D space[A].Behaviour Monitoring and Interpretation BMI[C].2007.77-90. [4] ERWIG M,SCHNEIDER M.Spatio-temporal predicates[J].IEEE Transactions on Knowledge and Data Engineering,2002,14(4):881-901. [5] SCHNEIDER M,TAO C,VISWANATHAN G,et al.Cardinal directions between complex regions[J].ACM Transactions on Database Systems,2012,37(2):1-45. [6] 高勇,刘瑜,邬伦,等.移动点对象与参考地物空间拓扑关系[J].计算机工程,2007,33(22):57-59. [7] NAET K S,KONG H,CHO M,et al.Multimedia information retrieval based on spatiotemporal relationships using description logics for the semantic web[J].International Journal of Intelligent Systems ,2006,21:679-92. [8] KURATA Y,EGENHOFER M J.The 9+-Intersection for Topological Relations between a Directed Line Segment and a Region[C].BMI,2007.62-76. [9] 杜世宏,王桥,李治红.GIS 中自然语言空间关系定义[J].武汉大学学报(信息科学版),2005,30(6):533-538. [10] 邓敏,马杭英.线与面目标间拓扑关系的层次表达方法[J].测绘学报,2008,37(4):507-513. [11] 杜清运.空间信息的语言学特征及其自动理解机制研究[D].武汉:武汉大学,2001. [12] 黄雪萍,邓敏,吴静,等.线面目标自然语言空间关系集成表达与描述方法研究[J].武汉大学学报(信息科学版),2013,38(2):230-234. [13] GÜTING R H,BÖHLEN M H,ERWIG M,et al.A foundation for representing and querying moving objects[J].ACM Transactions on Database Systems,2000,25(1):881-901. [14] 黄雪萍.基于地名信息的空间查询方法研究[D].长沙:中南大学,2012. Natural-Language Description of Spatio-temporal Relationships between Moving Points and Reference Features ZHANG Cai-li,WU Jing,DENG Min (SchoolofGeosciencesandInfo-Physics,CentralSouthUniversity,Changsha410083,China) Modeling spatio-temporal relationships between moving objects is of great significance for spatio-temporal queries,spatio-temporal analysis and reasoning.Based on the slice representation of moving point′s trajectory,a novel method is proposed to describe the spatio-temporal topological relationships between a moving point and reference feature.At the same time,an integrated framework is presented for the representation of spatio-temporal relationships between moving points and reference features according to the description rules of natural language,where the topological,directional and distance relations between moving points and reference features are considered together.Finally,a case study is provided to demonstrate the application and feasibility of the proposed method in this paper. moving objects;spatio-temporal relationships;natural language 2014-09-17; 2014-12-28 国家自然科学基金项目(41171351、40871180):中南大学中央高校基本科研业务费专项资金资助项目(2012zzts008) 张彩丽(1989-),女,硕士研究生,主要研究移动对象时空关系自然语言描述与智能查询。E-mail:renlisi888@126.com 10.3969/j.issn.1672-0504.2015.03.003 P208 A 1672-0504(2015)03-0012-05


2 集成方向、距离的复杂时空关系定义及描述

3 实验分析
4 结论

