狼群搜索算法在光伏阵列MPPT中的应用

张正文，谭文龙，潘 甲，范 斌

（湖北工业大学电气与电子工程学院，湖北武汉 430068）

狼群搜索算法在光伏阵列MPPT中的应用

张正文，谭文龙，潘 甲，范 斌

（湖北工业大学电气与电子工程学院，湖北武汉 430068）

光伏阵列最大功率点在外部环境条件变化时往往难以进行有效地跟踪，而传统的最大功率点跟踪（MPPT）方法常常会导致搜索陷入局部极值并且响应速度慢。针对此问题，本文提出一种基于狼群搜索算法的最大功率点跟踪方法。仿真结果表明：该算法能够有效地进行全局最大功率点跟踪，验证了该算法的可行性。关键词：光伏发电；最大功率点跟踪；狼群搜索算法

0 引言

太阳能作为可再生绿色能源，因其无污染、低成本、易获取的特点，已经成为代替传统能源的首选能源。但是，在实际的应用中，太阳能光伏发电系统中光伏阵列呈现非线性的特征，输出功率会随着日照以及环境温度的变化而变化，在不同的光照强度和环境温度下光伏阵列有不同的输出电压，但是只有在某一特定的电压下光伏阵列才能达到最大的输出功率［1－2］。因此，必须找到一种更为有效的最大功率点跟踪（MPPT）方法，使得光伏阵列达到最佳的转换效率。传统的MPPT方法有电导增量法、扰动观察法等，扰动观察法结构简单、被测参数少，电导增量法在外界环境迅速变化的时候，其动态性能和跟踪特性要优于扰动观察法。但是，这两种方法都有一个共同的问题，即步长固定。当步长过小时，光伏阵列就会长时间保持低功率输出，达不到最大功率跟踪的效果；但是如果步长过大，整个系统的振荡就会加剧，不利于系统的稳定性［3］。目前，随着智能技术的大力发展，其应用领域也越来越广泛。粒子群优化算法（PSO）和遗传算法（GA）逐渐应用于光伏发电领域。但是粒子群算法的搜索对象是基于理论的太阳能电池数学模型的输出功率表达式，由于理论与实际情况有一定的差距，当系统有扰动存在时，此方法无法根据实际情况来跟踪最大功率点；遗传算法具有并行搜索的能力，从解空间中多点出发搜索问题的最优解，但是遗传算法进行局部搜索的能力差，容易导致早熟［4－7］。这两种方法在应用时都需要引入其他的优化方法来确保能够搜索到全局最优解。因此，本文提出一种基于狼群搜索算法［8］（WCA）的光伏阵列MPPT控制方法，对光伏阵列模块进行最大功率点寻优，通过与粒子群算法［9－10］和遗传算法［11－12］的比较，WCA在收敛速度和求解精确度上都有较大的提高，最后，通过Matlab／Simulink建立仿真模型，仿真实验验证了该算法的可行性。

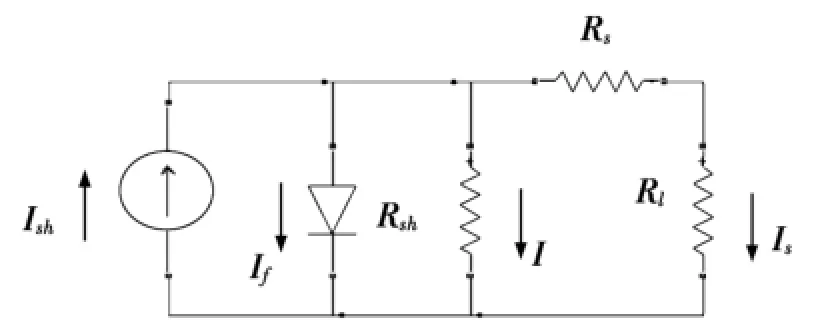
图1 光伏电池等效电路

1 太阳能电池等效电路分析

根据太阳能电池的基本工作原理，在理想情况下，光伏电池等效电路如图1所示，其中，Rs是由材料电阻、薄层电阻、电极接触电阻及电极本身传导电流的电阻所构成的总串联电阻；Rsh为旁路电阻；I为流过旁路电阻Rsh的电流；Is为负载电流，Ish为光电流；Rl为负载；If为逆向饱和电流。

此时可得光伏电池输出特性，负载电流为Is：

式中：Is为光伏电池输出电流；U为光伏电池输出电压；Ish为光电流；Ios为光伏电池的暗饱和电流；K1为短路电流的温度系数；ISCR为标准测试条件下光伏电池的短路电流；λ为日照强度；T为开式温度，K。

光伏阵列的输出特性方程为：

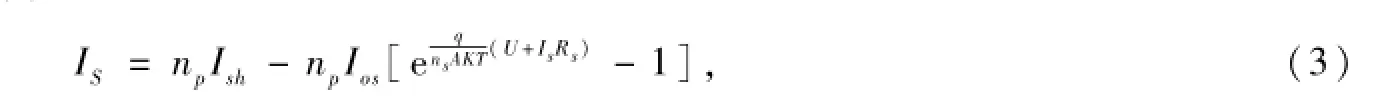
其中：np、ns分别为光伏阵列中光电池并联和串联的个数；A为二极管因子，A＝1～ 5；K为波尔兹曼常数，K＝1.38×10－23J／K；q为电荷量，q＝1.6×10－19C。

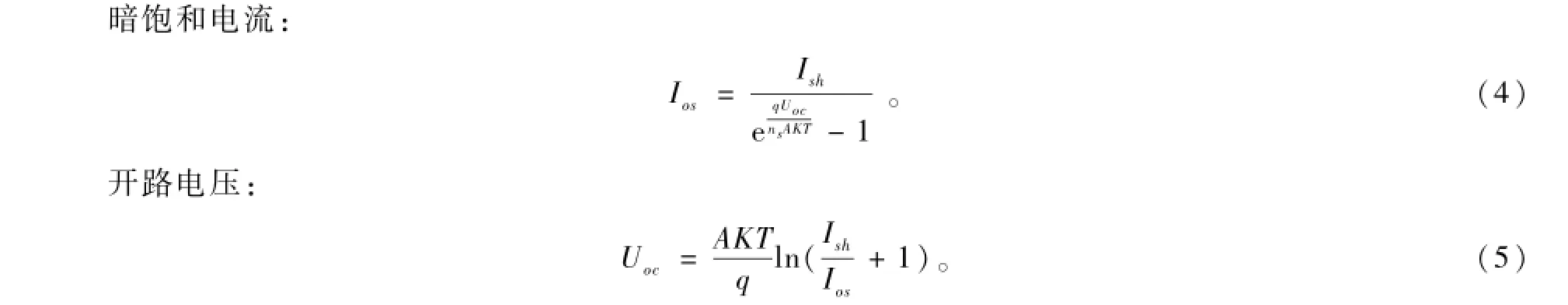
2 光伏电池板MPPT控制基本原理

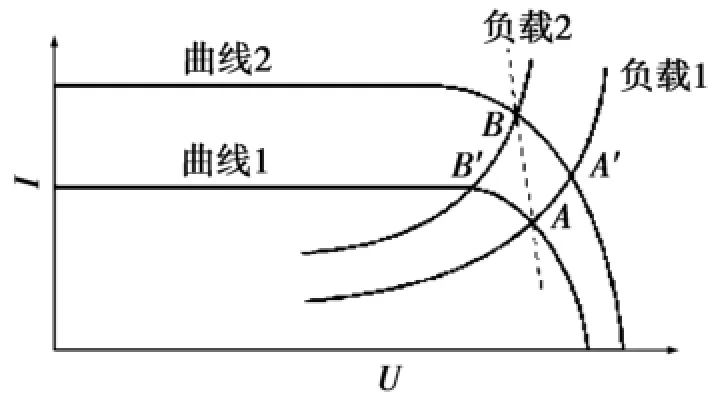
图2 光伏阵列I-U特性曲线

光伏阵列的短路电流和开路电压易受到日照强度和温度的影响，系统的工作点不固定，MPPT就是在光照和温度变化的条件下自寻优的过程。

3 基于狼群搜索算法的最大功率点跟踪

3.1 狼群搜索算法相关定义

该算法分为初始化狼群、竞争领导者狼、向领导者移动、包围猎物以及分配食物5个步骤。首先，定义狼群初始规模为N，搜索空间维数为D，第i只狼所处的初始化位置为Xi。在这N匹狼中选取q匹狼竞选领导者头狼，选取出来的q匹狼在自己周围的h个方向上进行搜索，其中第j个位置第d维的点为yjd，当这q匹狼的搜索次数大于最大搜索次数max dh或者搜索到的位置比当前位置差，则结束搜索行为。狼群通过向头狼移动来更新自己的位置，第i只狼第d维更新后的位置为Zid。淘汰最差的m匹狼，然后随机再生成m匹狼作为狼群更新的原则。

狼群搜索算法初始化位置、竞选公式和位置更新公式分别为：

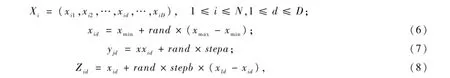
其中：rand为［－1，1］内均匀分布的一个随机数；xmax、xmin分别为搜索空间的上下限；stepa为搜索步长；stepb为移动步长。

包围公式和包围步长更新公式为：

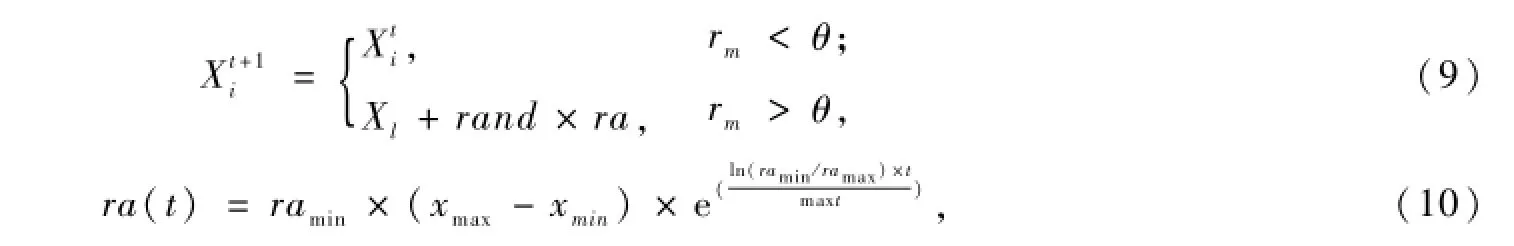
其中：rm为［0，1］内的随机数；ra为包围步长；t为当前迭代次数。

3.2 狼群搜索算法流程

广东印协是由省内印刷、复制企业，以及相关单位自愿组成的全省行业性、非营利性的社团组织，成立之初的本意在于加强印刷企业的团结与合作，提高从业人员的科学技术和管理水平，促进广东省印刷业的发展，且这样的精神一直贯穿至现在。三十九年间，协会名称几经改变，从“广东印刷学会”到“广东印刷技术协会”“广东省印刷协会”，直至现在的“广东省印刷复制业协会”，而每一次改名，都有着深深的时代烙印，并彰显出当时的责任之所在。

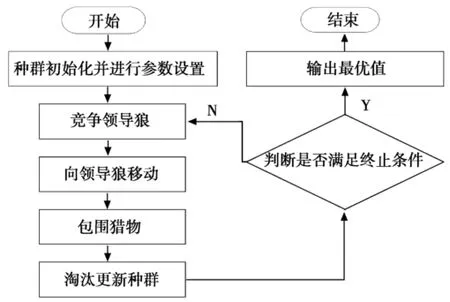
图3 算法流程图

狼群搜索算法在实际应用中为了获得最大的功率点，将每个潜在的最优解，即占空比D视作狼群中的一匹狼，通过占空比来控制输出电压，将光伏阵列的总输出功率P＝UI作为目标函数，算法的输入为光伏阵列的输出电压和电流，算法的最终目标是得到使目标函数值最大的最优解。算法流程图如图3所示。

3.3 算法对比分析

传统的光伏阵列最大功率点跟踪的方法有固定电压法、电导增量法、扰动观察法等多种方法，但传统的方法由于其容易陷入局部极值等固有的缺陷，并不适合用来提高光伏阵列的输出效率。而智能算法这类刚提出不久的算法相比传统的方法而言，在求解速度和精度上面有很大的提高，因而受到了广泛的关注。在此，为了能够直观地比较各个算法的性能以及本文算法的有效性，利用粒子群算法（PSO）、遗传算法（GA）这两种热门算法和狼群搜索算法（WCA）在不同函数下进行比较。在Matlab R2012a下进行仿真实验，实验在装有Windows XP操作系统的PC机上进行。PSO、GA、WCA具体参数设置如下：初始化规模为200，最大迭代次数为 800；PSO算法惯性权重w＝0.729 8，学习因子为 2；GA算法交叉概率gc＝0.8，变异概率gm＝0. 05；WCA算法竞争狼q＝5，搜索方向h＝4，最大搜索次数为15，搜索步长和包围步长分别为1.5和0.9，最差狼个数为5。对3个函数分别进行20次独立实验，分析每次实验所得的结果，比较在不同算法下分别求得的20个结果的平均值、标准差、最优值和平均耗时，实验结果如表1所示。

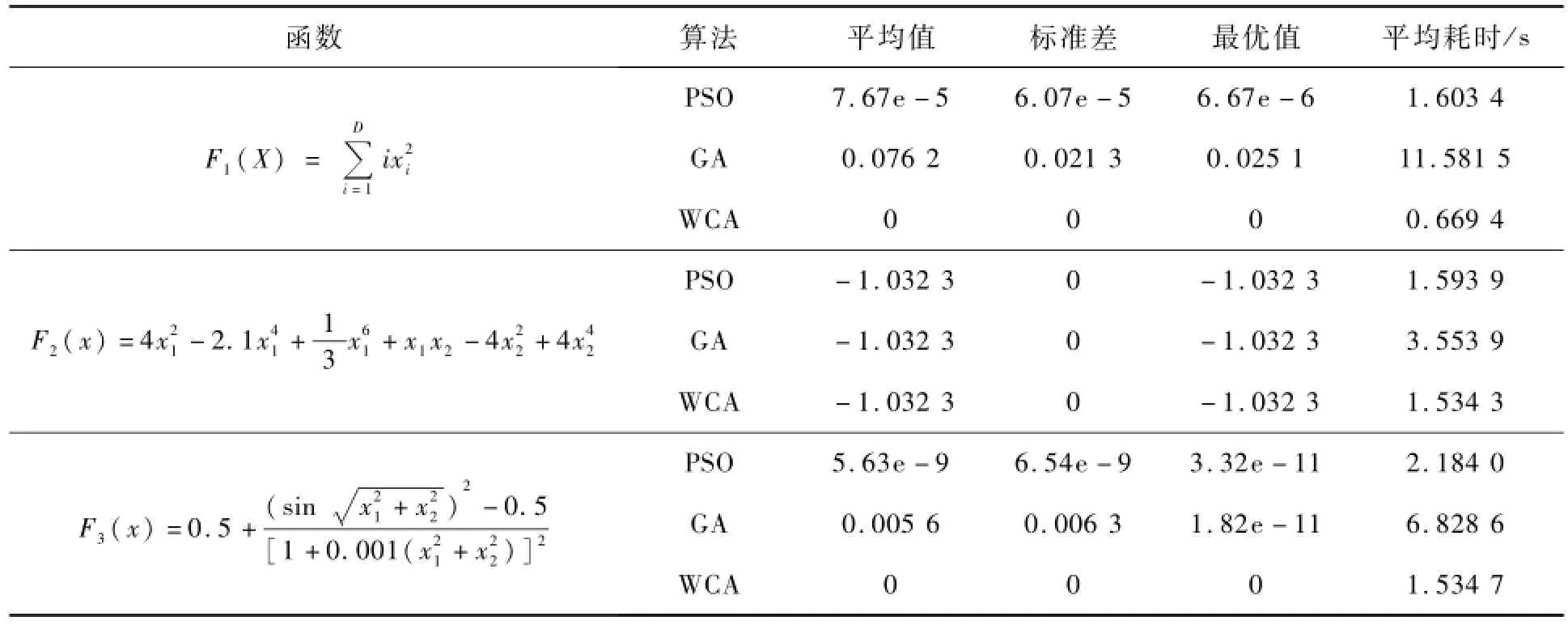
表1 算法对比结果

表1是对3个不同的函数在不同的算法上的测试结果。表1中平均值体现的是算法的寻优能力，标准差体现了该算法的鲁棒性，最优值体现了算法的收敛精度，平均耗时体现了算法的求解速度。分析实验数据可知：3种算法的寻优能力都较强，而WCA算法的标准差始终小于或等于其他两种算法，说明WCA算法在寻优过程中有良好的鲁棒性。从平均耗时上来看，GA算法计算时间相对较长，主要是因为该算法在求解过程中会导致大量无关的冗余迭代［13］。PSO算法中其粒子位置的更新单一地通过比较自身的位置与其周围位置和当前最优位置来进化，从而使得求解速度较快［14］。对于WCA算法，每次迭代计算后都会进行种群更新，加上该算法的部分参数是人工随机给定的，因而得到的平均寻优结果和耗时都最优。

综上可得WCA算法在求解精度上要优于PSO算法和GA算法，求得的值更接近理论值，而且WCA算法相对于其他两种算法在求解速度上也更快。

4 参数选取与仿真结果

种群初始化规模为30，最大迭代次数为200，q＝5，h＝4，max dh＝15，stepa＝1.5，stepb＝0.9，m＝5，θ＝0.2。本文仿真是利用Matlab／Simulink建立仿真模型［6］，如图4所示。

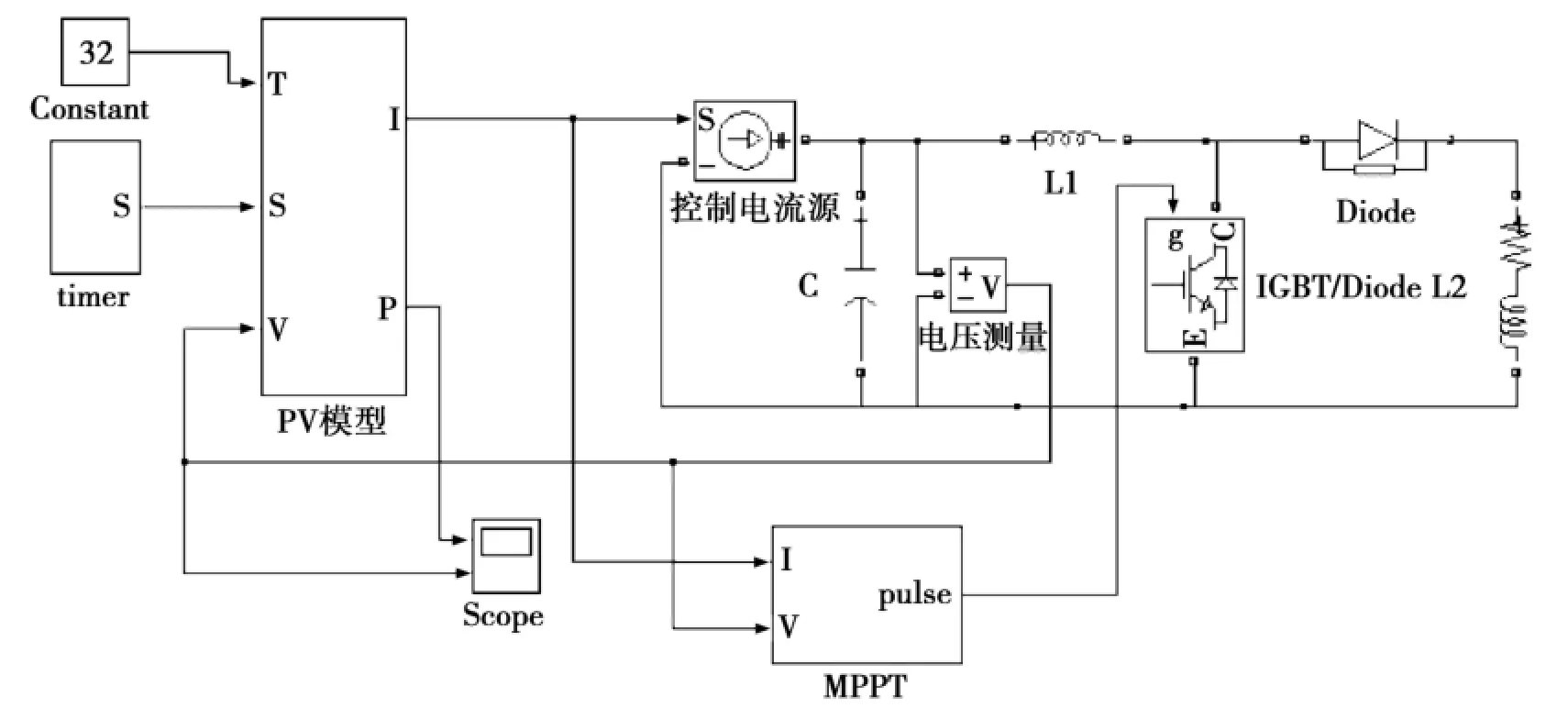
图4 MPPT仿真模型

仿真实验模拟两种不同的环境，一种在光照强度为1 000 W／m2，温度为25℃条件下；另一种在光照强度为600 W／m2，温度为23℃条件下。光照强度为1 000 W／m2、温度25℃条件下光伏特性曲线进行最大功率点跟踪，结果如图5a和图5b所示，图5a为P-U特性曲线，图5b为I-U特性曲线。

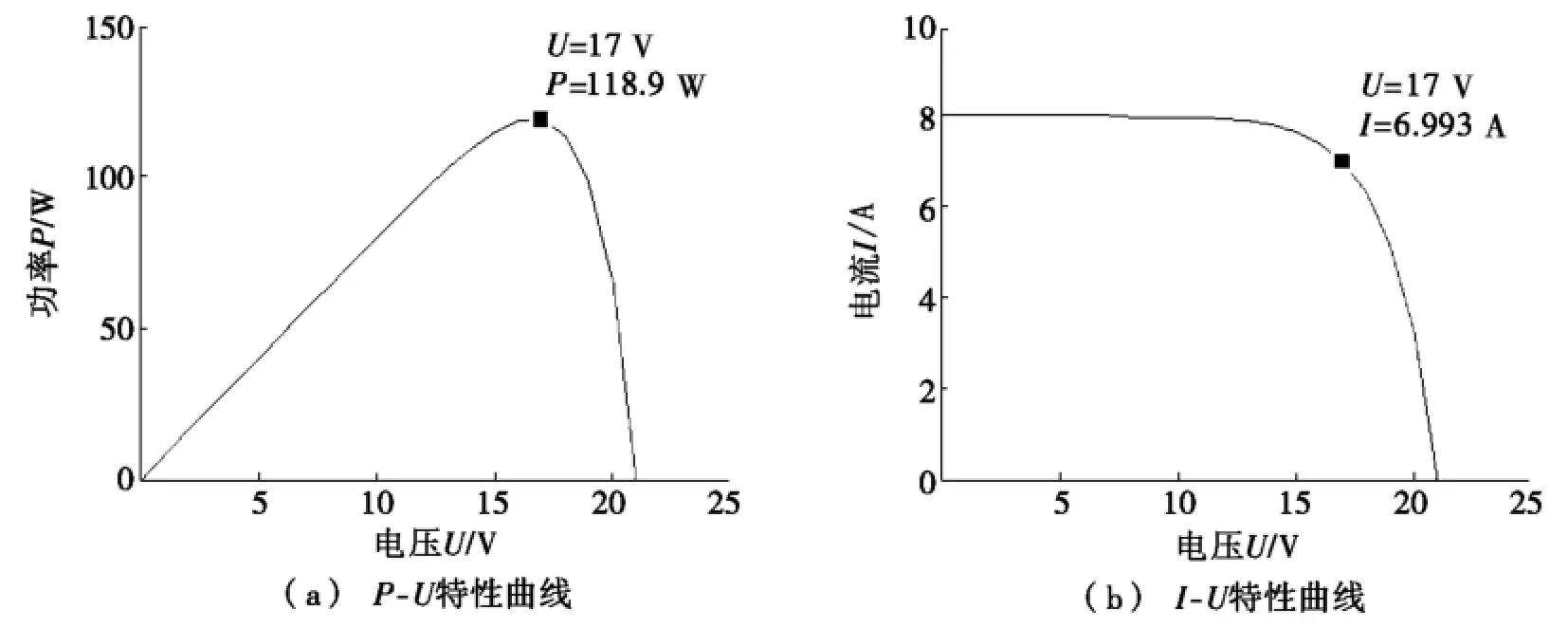
图5 光照强度1 000 W／m2、25℃条件下光伏特性曲线

光照强度为600 W／m2、温度为23℃条件下光伏特性曲线进行最大功率点跟踪，结果如图6a和图6b所示，图6a为P-U特性曲线，图6b为I-U特性曲线。

仿真结果显示：WCA算法的全局搜索能力可以锁定在一定条件下的光伏输出曲线的最大功率点（P-U曲线中的最高点）。

但是，需要注意的是，WCA算法的参数设置依赖于经验参数，并无过多的理论依据，因此，在一定的情况下可能会搜索不到全局最优值。

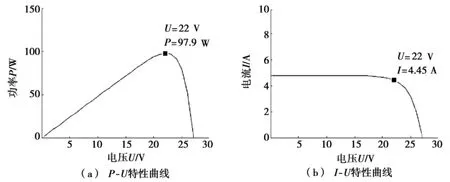
图6 光照强度600 W／m2、23℃条件下光伏特性曲线

5 结论

本文提出了一种新型的基于狼群搜索算法的光伏阵列最大功率点跟踪方法，并在Matlab／Simulink环境下建立仿真模型进行仿真。由仿真结果可以看出：通过WCA算法可以快速找到在不同的环境条件下光伏模块最大功率点，验证了该算法的可行性。本文提出的光伏阵列MPPT算法适用于模块化结构的光伏发电系统，该算法在仿真实验时并不考虑单一模块局部遮荫问题。

［1］ 徐瑞东，胡义华，陈昊，等.一种改进的光伏阵列最大功率点跟踪方法［J］.工矿自动化，2011，3（3）：25－28.

［2］ 王义飞，吴伟，杨宇.光伏系统最大功率点快速判断和跟踪方法［J］.系统仿真学报，2013，25（2）：389－393.

［3］ 崔岩，蔡炳煌，李大勇.太阳能光伏系统MPPT控制算法的对比研究［J］.太阳能学报，2006，27（6）：535－539.

［4］ 刘艳丽，周航，程泽.基于粒子群优化的光伏系统MPPT控制方法［J］.计算机工程，2010，36（15）：165－267.

［5］ 王长明，聂建军.基于遗传算法的二次曲面提取技术研究［J］.郑州大学学报：理学版，2013，45（1）：65－68.

［6］ 於世为，魏一鸣，诸克军.基于粒子群－遗传的混合优化算法［J］.系统工程与电子技术，2011，33（7）：1647－1652.

［7］ 牛向阳.基于遗传算法和BP算法的混合算法［J］.河南科技大学学报：自然科学版，2007，28（1）：46－48.

［8］ 周强，周泳权.一种基于领导者策略的狼群搜索算法［J］.计算机应用研究，2013，30（9）：2629－2632.

［9］ M iyatake M，Veerachary M，Toriumi F，et al.Maximum Power Point Tracking of Multiple Photovoltaic Arrays：A PSO Approach［J］.IEEE Transactions on Aerospace and Electronic Systems，2011，47（1）：367－380.

［10］ Jiang S，Cao D，Li Y，et al.Grid-connected Boost-half-bridge Photovoltaic Microinverter System Using Repetitive Current Control and Maximum Power Point Tracking［J］.IEEE Transactions on Power Electronics，2012，27（11）：4711－4722.

［11］ Ji Y H，Jung D Y，Kim JG.A Real Maximum Power Point Tracking Method for M ismatching Compensation in PV Array Under Partially Shaded Conditions［J］.IEEE Transactions on Power Electionics，2011，26（4）：1001－1009.

［12］ Zhou Y Q，Liu J K，Zhao G W.Leader Glowworm Swam Optimization Algorithm for Solving Nonlinear Equations Systems［J］.Electrical Review，2012，88（1b）：101－106.

［13］ Caamano P，Bellas F，Becerra J A.Evolutionary A lgorithm Characterization in Real Parameter Optimization Problems［J］. Applied Soft Computing，2013，13（4）：1902－1921.

［14］ Yu SW，Wei Y M.Hybrid Optimization Algorithm s Based on Particle Swarm Optimization and Genetic Algorithm［J］. Systems Engineering and Electronics，2011，33（7）：1647－1652.

TM 615

A

1672－6871（2015）05－0057－05

湖北省科技支撑计划基金项目（2014BAA135）

张正文（1965－），男，湖北黄冈人，副教授，硕士，研究方向为通讯工程、嵌入式.

2015－03－27