基于混合算法的车用传感器齿轮组优化设计

马 峻，刘本林

(北京电子科技职业学院，北京 100026)



基于混合算法的车用传感器齿轮组优化设计

马 峻，刘本林

(北京电子科技职业学院，北京 100026)

针对电动助力转向系统中的转矩传感器进行改进设计，实现了转矩和转角信号的一体化测量，节约了空间。建立了传感器齿轮组的数学模型，根据其使用特点，设定了数学模型的边界条件，并利用遗传算法与粒子群算法相结合的混合算法对齿轮系统的参数进行了优化设计，使传感器的质量和体积均有所下降，通过与传统设计方法及惩罚函数优化法相比较，混合算法优化的效果更佳。

电动助力转向系统；转矩转角传感器；齿轮优化；遗传算法；粒子群算法

0 引言

电动助力转向系统(EPS)通过传感器采集车速、发动机转速、方向盘转向、转角、驾驶员输入转矩等信号，并据此进行转向助力矩的分配，其中转矩传感器和转角传感器是保证准确分配转向助力及维持系统稳定工作的重要部件。目前国产EPS采用的是分别安装转矩、转角传感器或是仅安装转矩传感器的方法来获取相关信号，但这样的系统结构复杂，稳定性差，且分别安装的传感器占用一定空间。随着汽车电子技术的发展，整车电子的集成控制是大势所趋，将转矩、转角以及转动方向的测量集成到单一传感器上进行是必然选择。因此设计高精度、低成本、具有自主知识产权的转矩转角一体化传感器是发展国产EPS重要的内容之一。

1 转矩转角传感器设计

1.1 传感器芯片选择

目前的转矩传感器芯片主要有电位计式、光电式、电感式及磁阻式等。日本 NSK 公司的电位计式传感器[1]采用滑套机构将转角差变换为电位计摆臂机构的摆动，实现转矩测量，但该种传感器属于接触式传感器，存在磨损问题，其精度会受到影响。为克服接触式传感器的磨损问题，日本的NSK公司[2]以及KOYO公司[3]相继推出了磁电式非接触传感器，具有较高的精度，很好地实现了非接触测量，但抗电磁干扰能力较差，在电磁强度较大的城市中其使用精度会受一定影响。美国LUCAS 公司生产的光电式传感器实现了非接触的高精度测量[4]，但其结构比较复杂，对加工工艺要求较高，此外光电式传感器对工作环境要求较高，不适宜应用于汽车上。清华大学季学武副教授等曾对其进行改进，但存在温度漂移和绕线的问题[5]。因此考虑选用基于巨磁电阻原理的TLE5011角度传感器作为本传感器的芯片，它能够较好满足车用传感器的使用条件。

1.2 传感器结构设计[6]

图1 传感器齿轮组布置

2 传感器齿轮组优化

2.1 传感器齿轮系统数学模型的建立

2.1.1 变量的选择

以大齿轮1、双联齿轮3以及小齿轮6啮合的传动机构为例，建立其数学模型。设计变量为传动比i，齿数z，模数m，齿宽B，变位系数xm表示为

X=[x1、x2、x3、x4、x5、x6、x7、x8、x9、x10]T

2.1.2 目标函数的推导

在传感器齿轮机构中，各齿轮的体积越小，其原料成本越低，同时其质量也降低，其圆周速度和转动惯量随之减小，测量中的芯片受到齿轮系统的动载波动量减小。这样的齿轮系统在传感器中可以有效提高测量精度。因此函数推导中应以所有齿轮质量之和最小为目标函数，由于采用塑料材质，其密度一定，目标函数可以转化为所有齿轮体积之和最小。

大齿轮1的质量

双联齿轮3的质量

小齿轮6的质量

齿轮系统总质量：Mtotal=M1+M3+M6

由以上推导可见，齿轮系统总质量Mtotal仅与模数m、齿数z以及齿宽B相关，因此，这些即为函数的变量，即：

将它们作为设计齿轮系统的变量，并表示为

X=[x1、x2、x3、x4、x5、x6、x7、x8]T

则目标函数表示为

F(X)=V=f(x1、x2、x3、x4、x5、x6、x7、x8)

其中模数m1，m2按照国家标准选出，为离散变量；齿数为整数型连续变量，齿宽为实数型连续变量。

2.1.3 约束条件的确定

齿轮压力角、齿顶高系数、顶隙系数分别取标准值α=20°，ha*=1，c*=0.25，做为非接触式传感器齿轮系统，其受力较小，因此选用巴斯夫[7]推出的高流动性Ultradur High Speed( PBT-聚对苯二甲酸丁二醇酯)，其密度为1.3 g/cm3。

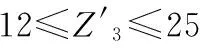
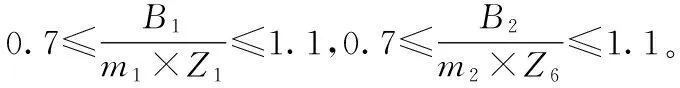
根据齿轮设计手册，齿轮接触强度应小于其许用应力[8]，即：

式中：ZE为PBT材质在60 ℃时弹性影响系数,ZE=12.4；K为强度载荷系数，K=KAKVKαKβ；KA为工况系数；KV为动载系数；Kα为齿间载荷分布系数；Kβ为齿向载荷分布系数。

根据工况，选取参数KA=1.25，KV=1.05，Kα=1.2，Kβ=1.4+0.23×10-3B。

齿轮受力为

式中T为转矩。

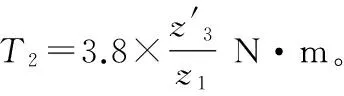
图2 中国驾驶员偏好的转向力随侧向加速度的变化曲线

查表确定PBT材料的许用应力为60MPa，将其代入公式得：

齿轮弯曲强度也应小于许用应力值，即：

查表确定PBT材料的弯曲强度许用应力值为100 MPa，将其代入公式得：

2.1.4 优化数学模型的建立

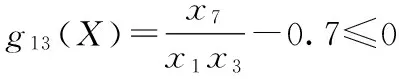
弯曲强度约束函数为：

2.1.5 齿轮组优化方法设计

通过数学模型的建立，发现这是一个有2个离散变量，6个连续变量，20个不等式约束条件组成的非线性优化设计问题。

此类问题常用的优化设计算法主要有梯度法、牛顿类法[10-11]、变尺度法[12]、惩罚函数法[13]、遗传算法[14-15]等。在非线性问题优化方法中，遗传算法(GA)是对问题变量的编码集进行操作，从一个点群开始寻优，因此可以获得全局最优解，具有广泛的实用性。但遗传算法更适合求解离散变量，求解连续变量优化问题时，常采用粒子群算法(PSO)。而对于齿轮优化类的复杂问题，遗传算法与粒子群算法的混合模式(GA-PSO)比其他类型算法的混合模式具有更好的优化效果[16]。

混合算法中以遗传算法为基础，进行原始种群的产生、选择、交叉、变异等计算，同时为提高连续变量的优化水平，选取部分基因，固定其中的离散变量值，再采用离子群法对连续变量值进行优化计算，然后将结果替换原始种群，返回遗传算法，循环上述规则，直至满足终止条件。其总体流程如图3所示。

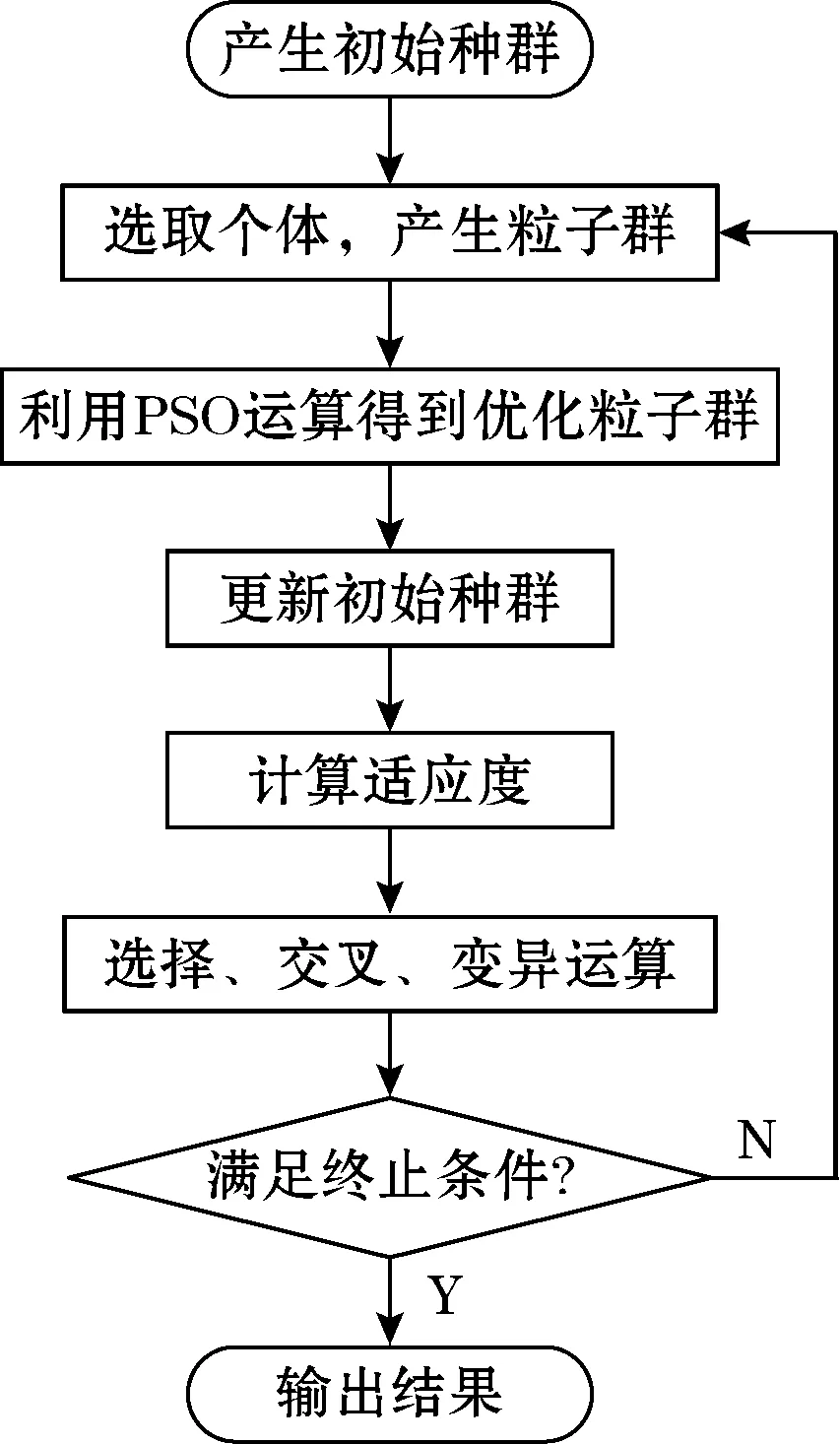
图3 GA-PSO混合算法总体结构流程图

2.1.6 混合算法中PSO运算的实现过程

步骤1：随机产生多组编码与固定的离散变量组成粒子群；

步骤2：计算每个粒子的适应函数；

步骤3：更新个体最佳位置(Pi)；

步骤4：更新全局最佳位置(Pg)；

步骤5：更新粒子的速度和位置，由于本优化中有6个连续变量，所以每个粒子中有6个分量。每次迭代中粒子i根据Pi和Pg调整速度vi=(vi1，vi2，vi3，vi4，vi5，vi6)和位置Xi=(xi1，xi2，xi3，xi4，xi5，xi6)。

式中：k为迭代次数；c1、c2为学习因子，取非负常数；r1、r2为[0,1]范围内的随机数；pid为个体i在历史最佳位置的第d个分量；pgd为全局最佳位置的第d个分量；ω(k-1)为惯性权重系数，进化过程中按下式线性减小。

式中:kmax为最大进化代数；ωmax和ωmin是ωk的取值范围。

步骤6：判断是否满足终止条件，如果满足，则终止循环;如果不满足，则回到步骤2，直至找到最优解，输出优化粒子群。

2.1.7 计算结果比较

表1中列举了传统设计法、惩罚函数内点法优化与GA-PSO混合算法的计算结果。

3 结论

本文为EPS设计了一种转矩转角一体化传感器，并利用遗传算法与粒子群算法的混合模式对齿轮参数

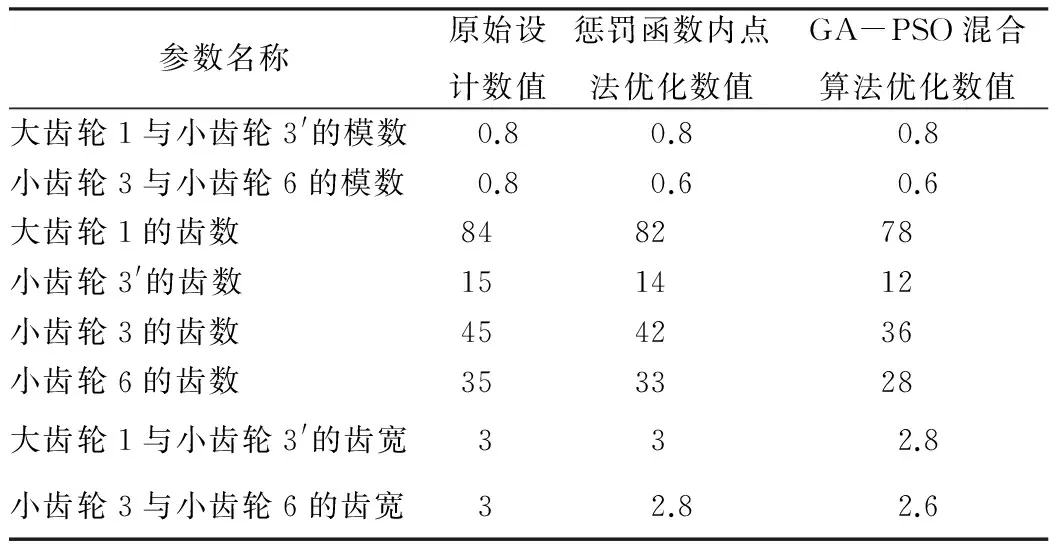
表1 优化前后参数对照表

进行优化。优化后的传感器齿轮系统质量、体积有所下降，测量精度基本符合要求。

[1] NOGUCHI A，YAMAWAKI K，YAMAMOTO T，et al．Development of a Steering Angle and Torque Sensor of Contact-type .Furukawa Review,2004(25):36-41．

[2] KOZAKI Y，HIROSE G，SEKIYA S，et al．Electric Power Steering (EPS).Motion &Control .No.6-1999 NSK:9-15．

[3] OSUKA A,MATSUOKA Y,TSUTSUI T,et al.Development of pinion-Assist type electric power steering system .KOYO Engineering Journal Edition,2002，161：46-51．

[4] HAZELDEN R J.Optical torque sensor for automotive steering systems.Sensors and Actuators A,1993(37/38):193-197．

[5] 季学武，马小平，周寒露，等.电动助力转向系统光电式转矩传感器的研究.仪表技术与传感器,2004(4):65-67．

[6] 马峻,刘本林.车用转矩转角传感器无侧隙齿轮系统设计.仪表技术与传感器,2014(4):77-80．

[7] 巴斯夫．High Speed用于博世方向盘转角传感器生产.轿车情报，2008(3)：211．

[8] 朱孝录.齿轮材料的接触疲劳强度.机械传动,1994(9):34-37．

[9] 宗长富，麦莉，王德平，等.基于驾驶模拟器的驾驶员所偏好的转向盘力矩特性研究.中国机械工程，2007(4):1001-1005.

[10] FLEURY C,SANDER G.Relations between optimality criteria and mathematical programming.Proc.Symposium on Applications of Computer Methods in Engineering,Los Angeles,1977．

[11] KHOT N S，BERKE L,VENKAYYA V B． Comparison of optimality criteria algorithms for minimum weight design of Structures.Structural Dynamics and Materials Conference,1978．

[12] 赵又红,符炜,罗显光.二级圆柱齿轮减速器的多目标优化设计.湘潭大学学报(自然科学版)，2003,25(2):81-84．

[13] 韩伯顺.非线性规划中的罚函数及填充函数方法:[学位论文].上海:上海大学,2006．

[14] SHI L S,LJ Z Y.An improved pareto genetic algorithm for multi-ojective TSP．The 5th International Conference on Natural Computation(ICNC2009),Tianjin,2009．

[15] LIU Q.Study on multi-object optimization of logistics network based on genetic algorithm.2008 International Conference on Computational Intelligence and Security(CIS2008),Suzhou,2008．

[16] 梁艳春,吴春国,时小虎.群智能优化算法理论与应用.北京:科学出版社,2009.

Optimization Design of Sensor Gear Set Applied in Automobile Based on Hybrid Algorithm

MA Jun，LIU Ben-lin

(Beijing Polytechnic Automobile School，Beijing 100026,China)

The design of torque sensor in the EPAS was improved,the integration of torque and angle signal measuring was realized and the space was saved.The mathematical model of the sensor gear set was established and according to the characteristics of its use,the boundary conditions for the mathematical model were set.The hybrid algorithm combining the genetic algorithm and the particle swarm optimization was used to optimize the parameters of the gear system,which declined the quality and volume of the sensor.Compared with the traditional design methods and the penalty function optimization ,the optimization effect of this hybrid algorithm is better.

electric power steering system；torque and angle integration sensor；gear optimization design;genetic algorithm;particle swarm optimization

北京高等学校“青年英才计划”资助项目(YETP1798)；科研基地-汽车技能大师工作室建设(国家改革试点项目2012)(PXM2012-014306-000177)

2014-05-06 收修改稿日期：2014-11-08

TP212

A

1002-1841(2015)04-0093-03

马峻(1980— )讲师，硕士， 研究方向为汽车制造技术。Email:majundky@126.com