基于DBN-ELM的球磨机料位软测量方法研究

康 岩,卢慕超，阎高伟

(太原理工大学信息工程学院,山西太原 030024)



基于DBN-ELM的球磨机料位软测量方法研究

康 岩,卢慕超，阎高伟

(太原理工大学信息工程学院,山西太原 030024)

针对采用传统方法建立球磨机料位软测量模型存在测量精度不高和稳定性较低的缺点，提出一种结合深度信念网络和极限学习机的软测量方法。该方法以球磨机轴承振动信号为辅助变量，采用深度信念网络进行振动信号功率谱的特征提取，然后将提取的有效特征输入极限学习机进行模型训练，得到软测量模型。最后在小型实验室球磨机上进行试验和模型验证。结果表明，该方法与传统方法相比具有较高的测量精度和较好的稳定性。

球磨机料位;深度信念网络;特征提取;极限学习机;软测量

0 引言

球磨机是广泛应用于电力、磨矿和化工等行业的高能耗设备。球磨机筒体内的料位是影响球磨机系统高效和安全稳定运行的关键因素之一，料位过低时球磨机的生产效率较低，料位过高时容易发生堵磨等安全事故。在实际工业生产过程中，由于球磨机筒内情况复杂，存料量难以直接测量，大部分球磨机系统未能高效运行[1]，因此，准确地测量球磨机料位对保障球磨机系统高效和安全运行具有重要意义。

近年来，科研技术人员针对该问题提出了很多解决方法，其中以软测量方法为主要代表，该方法主要是采用特征提取结合机器学习方法进行建模。文献[2]基于振动信号和反向传播神经网络建立了球磨机料位的软测量模型。文献[3]采用主成分分析(Principle Component Analysis,PCA)方法进行振动信号的特征提取，然后采用偏最小二乘回归方法(Partial Least Square Regression,PLSR)建立料位软测量模型。文献[4]采用偏最小二乘法(Partial Least Square,PLS)进行振动信号的特征提取，然后采用极限学习机(Extreme Learning Machine,ELM)建立料位软测量模型。

最新的神经网络研究成果表明，深度信念网络(Deep Belief Network，DBN)是一种深层神经网络，具有良好的特征学习能力，使分类或预测更加容易[5]。在特征学习和机器学习领域，包括人脸识别、语音识别、自然语言处理等方面，基于DBN提取的特征分类结果优于PCA、PLS方法[5-6]，同时DBN也成功应用于时间序列分析和预测[7]，已成为机器学习领域研究的前沿。其主要优势在于：通过逐层特征抽取，得到原始数据更加有效的深层次表示；通过逐层预训练的自学习方法使得DBN能通过大量无标记数据样本学习到所有层(不包括最终分类层)的最佳初始权值，获取数据的非线性特征；可通过少量带标记样本进行微调，对权值进行修正，使网络达到理想的性能。DBN的上述特性非常适合于求取振动信号的非线性特征表示，并且也适合于解决生产过程中球磨机料位精确样本难以获取的问题。极限学习机是由黄广斌等提出的一种针对单隐含层前馈神经网络的学习算法，具有学习速度快、泛化性能好等优点[8]。

综上，将DBN与ELM相结合的方法用于球磨机料位软测量建模，并在小型实验室球磨机上进行试验。试验结果表明该方法直接利用深度信念网络输出的特征信息，避免了复杂的特征选择过程，具有测量精度高、稳定性好的优点，为球磨机料位测量研究和实际应用提供了新的思路和方法。

1 理论与算法

1.1 深度信念网络

深度信念网络是一种近年来受到广泛关注的深层神经网络，其目标在于学习数据的深层次特征[9]。传统的神经网络也试图通过多层次的网络结构去学习更加深刻的特征，但是多层神经网络很难通过单纯的梯度下降法训练达到良好的效果[10]。深度信念网络采用逐层的无监督预训练机制较好地解决了该问题[11]。深度信念网络可以看作由若干层受限玻尔兹曼机(Restricted Bolzmann Machine,RBM)堆叠而成。另外，顶层附加一层有监督网络层，微调整个DBN网络权值，DBN网络结构如图1所示。

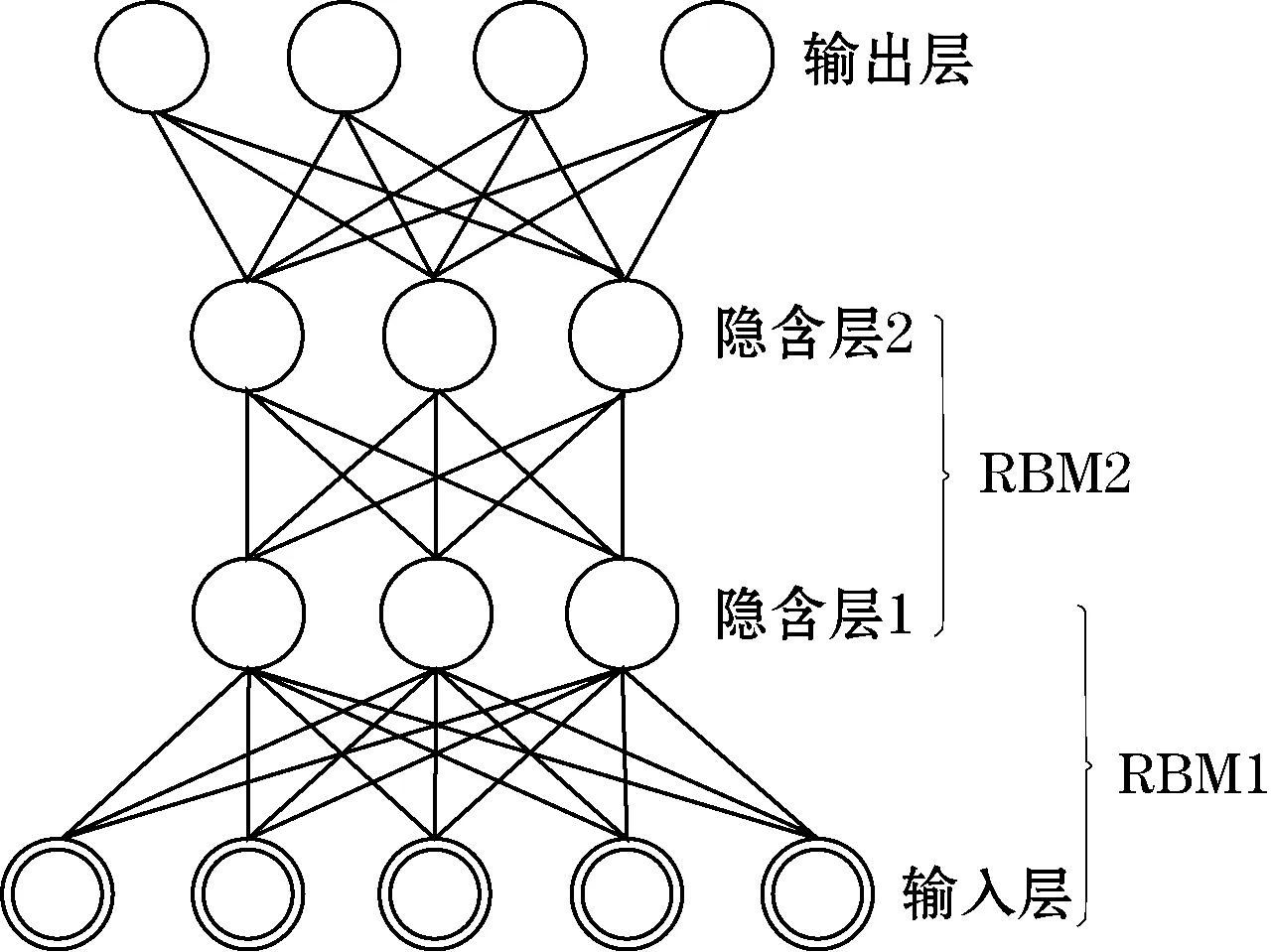
图1 深度信念网络结构图

RBM是一种两层随机神经网络，包含1个可见层和1个隐含层。每个神经元都与另一层的神经元相连接，而相同层的神经元之间无连接。RBM的主要功能是确定其输出层的概率分布。DBN将若干层RBM堆叠在一起，底层RBM的输出层(隐含层)作为上层RBM的输入层(可见层)，如此连接若干个RBM构成DBN网络。试验中，采用对比散度方法[11](Contrastive Divergence,CD)来逐层训练RBM，具体算法如下：

设z是输入数据，h是隐含层向量，v是可见层向量，ε是学习速率，w是RBM的权值矩阵，b是输入层(可见层)的偏置向量，c是输出层(隐含层)的偏置向量。

(1) 随机初始化模型参数θ0=(b0,c0,w0),并设定迭代次数Step。

(2) 将原始向量z赋值给RBM的隐含层向量v0。

(3) 通过公式(1)和式(2)计算向量h0,v1,h1的状态值，即隐含层或可见层的激活概率为

(1)

(2)

其中，激活函数σ(x)=1/[1+exp(-x)]。

(4) 利用公式(3)进行模型参数θ的更新，即权值w和偏置向量b,c的更新。

(3)

(5) 若t≥ Step，则训练结束，否则将θt-1赋值给θt,并转步骤3。

上述步骤中数学公式的推导过程可详细参阅文献[11]。文中DBN算法采用Palm所编写的MATLAB工具箱实现[12]。

1.2 极限学习机

极限学习机是一类针对单隐含层前馈神经网络(Single-hidden Layer Feedforward Network,SLFN)的学习算法。设训练集样本为[xi,yi]，i=1,2,…,k，ELM的隐含层单元个数为l，则ELM模型的输出为

(4)

式中：β为隐含层和输出层之间的连接权值矩阵；g(x)为隐含层的激活函数，可取sigmoid、sine或RBF函数等；a为输入层和隐含层之间的连接权值矩阵；d为隐含层的偏置向量。

存在a,d,β使得o与y近似相等，即：

(5)

式(5)可由矩阵表示为

HΒ=Y

(6)

式中H被称作网络的隐含层输出矩阵。

从而，隐含层和输出层之间的连接权值β可由公式(6)的极小2-范数最小二乘解得：

(7)

式中H+为隐含层输出矩阵H的Moore-Penrose广义逆。

2 球磨机料位软测量建模及实验

2.1 基于DBN-ELM的软测量建模

软测量技术主要依据对可测易测过程变量(称为辅助变量)与难以直接检测的待测变量(称为主导变量)的数学关系认识，采用计算方法实现待测变量的测量或估计[13]。文中以球磨机轴承振动信号为辅助变量，结合特征提取方法DBN和机器学习方法ELM建立球磨机料位的软测量模型。具体建模步骤为：

(1) 采集不同料位下的球磨机轴承振动信号；

(2) 对采集所得振动信号进行预处理，主要包括功率谱计算和谱段分割，获得基本特征向量；

(3) 采用DBN对所得基本特征向量进行特征提取和降维；

(4) 将提取的有效特征输入ELM模型，进行模型训练；

(5) 将测试数据输入已经训练好的DBN-ELM模型，进行模型测量效果验证。

2.2 试验过程

本研究通过在小型试验室球磨机上进行试验，获取试验样本数据。该球磨机尺寸为Φ360 mm×450 mm，由功率为2 kW的电动机进行驱动，转速由变频器调至60 r/min。在球磨机的远离电动机一端的轴承底座下放置1个振动传感器，用于采集不同料位下的轴承振动信号。数据采集系统主要由振动传感器、信号放大和滤波电路模块、USB数据采集器和上位机组成。上位机采用LabVIEW编写程序，用于观测信号波形和存储数据，同时将采样频率调至50 kHz，确保获取不失真的数据样本。

具体试验过程为，在一定的钢球装载量和转速下，从零料位开始，每增加1 L物料，记录60 s的振动信号。试验结束时，筒内料位为20 L，共采集得到20组数据，每组数据的采样点数为3×106个。以131 072为单位长度将每个料位下的数据分割为22个样本。每个料位下，任意取15个样本作为训练集，其余7个样本作为测试集，最后得到的训练集样本个数为20×15=300个，测试集样本个数为20×7=140个。

筒内料位的变化往往引起振动信号频域结构的变化。因此，采用Welch方法对每段时域信号进行功率谱(Power Spectrum Density,PSD)计算。图2为不同料位下振动信号的功率谱图。分析发现，球磨机轴承振动信号的有效频带范围为600～6 000 Hz。为便于数据处理并提高运算效率，以20 Hz为单位对有效频段进行分割并求均值。则最终得到的每个样本的维度为(6000-600)÷20=270。因此最终的训练集规模为300×270，测试集规模为140×270。

图2 振动信号的功率谱图

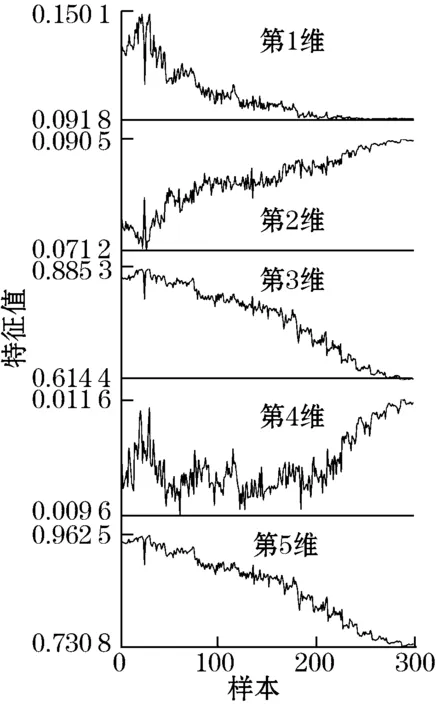
将训练集数据输入DBN模型进行特征提取和降维，试验所采用的DBN由2个RBM堆叠而成，第1个隐含层的单元个数为50，第2个隐含层的单元个数为30。由于篇幅所限，此处只列举DBN提取的前10维的特征值随料位变化的趋势图，如图3所示。可以看出，特征值随着料位变化而变化，且具有多维正相关关系(如第2维、第9维)和多维负相关关系(如第3维、第5～第8维、第10维)，这是PCA和PLS所没有的特性。然后将降维之后的30维特征向量输入隐含层节点个数为50的ELM进行模型训练。最后，采用测试集数据进行DBN-ELM模型的测量效果验证。

2.3 结果分析与对比

为验证DBN-ELM模型的有效性，将其与传统回归方法PCR和PLSR以及特征提取结合机器学习方法PCA-ELM和PLS-ELM进行比较。采用均方根误差(root-mean-square error,RMSE)进行测量效果评价。

(8)

考虑到ELM模型初始化的随机性，采用10次测量结果的平均RMSE来评价测量精确度。最后所得的测量曲线和平均RMSE分别如图4和表1所示。

表1 测量结果及参数设定

(a) PCR

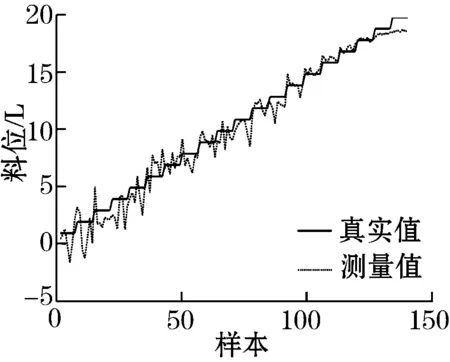
(b) PLSR

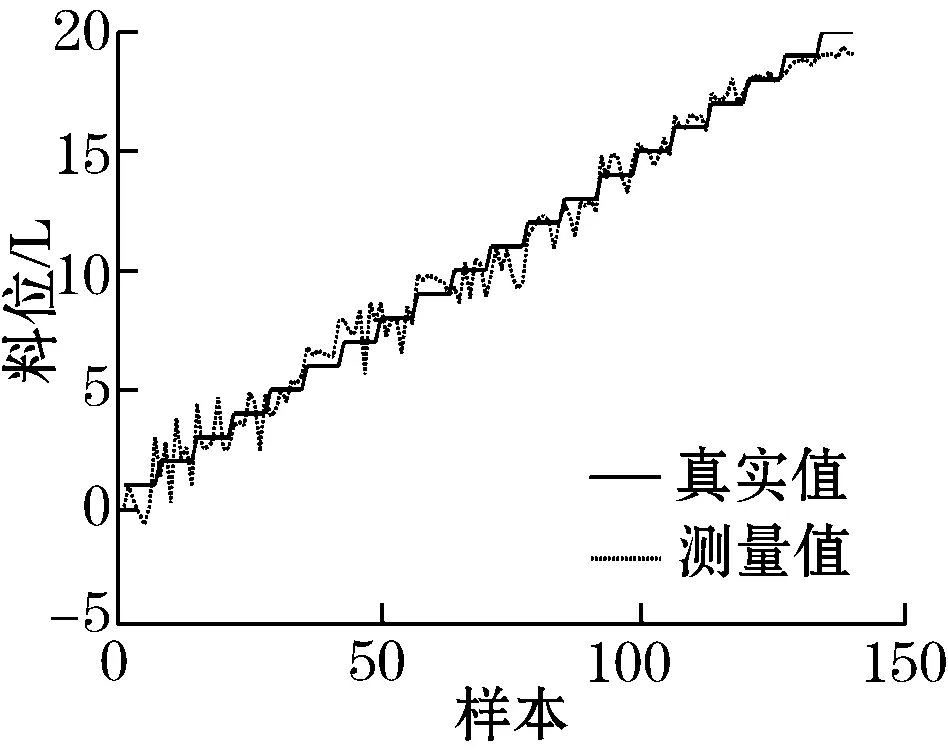
(c) ELM

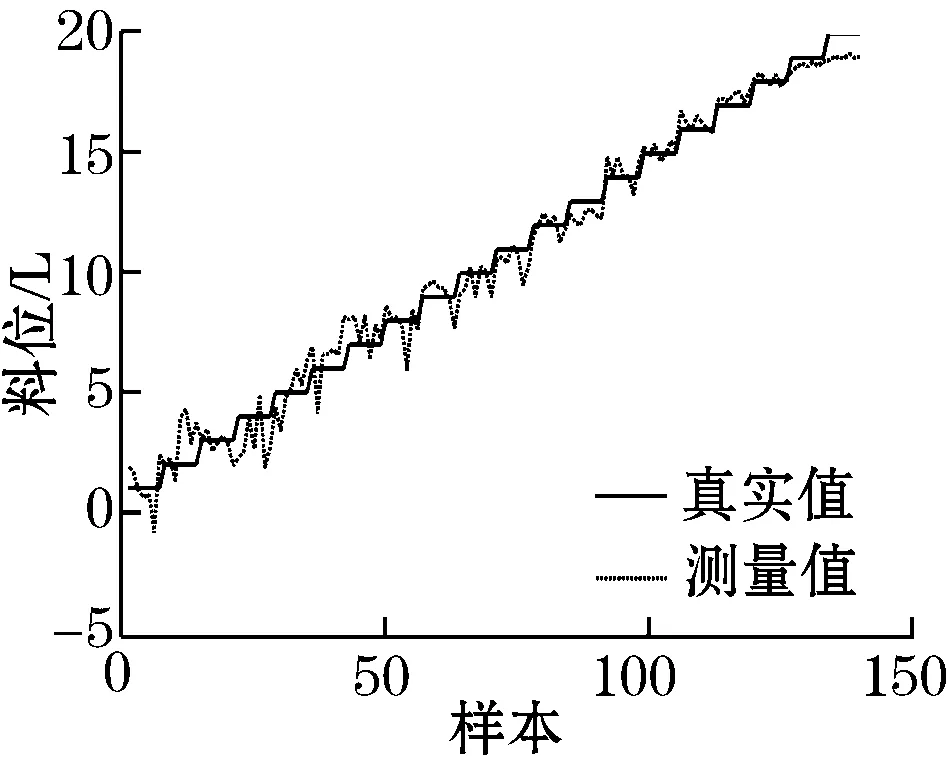
(d) PCA-ELM

(e) PLS-ELM

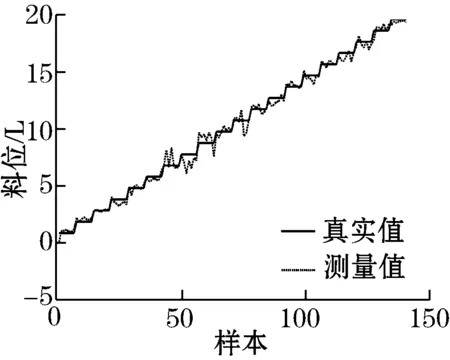
(f) DBN-ELM

表1中Ncomp=30表示PCA和PLS提取前30个主元，DBN则提取出30维有效特征信息；Nhide表示ELM模型的隐含层单元个数。从表1的平均RMSE可以看出，基于ELM的软测量方法比基于PCR和PLSR回归方法的测量精度高，体现了单隐含层神经网络处理非线性数据的有效性。此外，结合特征提取和ELM模型的方法即PCA-ELM,PLS-ELM和DBN-ELM的测量精度比单纯的ELM方法更高。这是因为分割之后的功率谱段中仍含有冗余信息和干扰信息，经过有效特征提取之后，筛选出主控因素，使得模型的测量精度提高。显然，基于相同参数设定的ELM模型，DBN-ELM方法是所有对比方法中测量精度最高的，体现了DBN比传统的PCA和PLS方法具备更好的特征提取能力。DBN通过逐层特征变换和抽取，可以提取更深刻的特征信息，克服了PCA和PLS无法提取非线性信息的缺陷。从图4可以看出，PCR和PLSR方法的测量曲线在中、低料位段的跟踪性较差；与它们相比，ELM、PCA-ELM和PLS-ELM方法的测量曲线的跟踪性在中、低料位段均有所改善，但是在高料位阶段的跟踪效果仍然较差；DBN-ELM方法在低料位段和高料位段的跟踪效果与其他方法相比优势比较明显，测量精度大幅度提高，验证了DBN优异的特征提取能力。

同时为分析各个方法的稳定性，将10次测量结果通过箱线图表示为图5。由图5可以看出，传统的PCR和PLSR回归方法虽然具有较高的稳定性，但是测量精度不高。由于ELM模型初始化的随机性导致其稳定性较差，经过PCA和PLS 2种特征提取方法进行主控因素提取之后，模型的稳定性得到改善，但是各自仍存在一次异常值。而基于DBN-ELM模型的方法，不仅具有较高的测量精度，而且其稳定性相对于ELM有很好的改善。

图5 10次测量结果的箱线图

综上所述，基于DBN-ELM模型的球磨机料位软测量方法，在测量过程中采用DBN提取了功率谱信号中能有效表征料位变化的信息，然后将其输入本身具有较高泛化性的ELM模型进行料位测量。试验结果表明，该方法不仅具有较高的测量精度，而且稳定性较好，具有良好的推广性。

3 结束语

为解决球磨机筒内料位难以直接测量的问题，提出了一种基于DBN-ELM模型的软测量方法。试验发现，在ELM建模之前，对数据样本采用DBN进行特征提取，与PCA和PLS特征提取方法相比，可以有效提高测量精度，DBN-ELM的测量精度比PLS-ELM提高了26%。DBN独特的特征提取机制能够有效克服PCA和PLS不能提取非线性特征的缺陷。同时DBN也很好地改良了基于ELM软测量模型的稳定性。

[1] 王东风,韩璞.基于RBF神经网络的球磨机负荷软测量.仪器仪表学报,2002,23(3):311-313.

[2] 沙毅,曹英禹,郭玉刚.磨煤机振声信号分析及基于BP网的料位识别.东北大学学报,2006,27(12):1319-1323.

[3] 汤健,郑秀萍,赵立杰,等.基于频域特征提取与信息融合的磨机负荷软测量.仪器仪表学报,2010,31(10):2161-2167.

[4] TANG J,WANG D H,CHAI T Y.Predicting mill load using partial least squares and extreme learning machines.Soft Computing,2012,16(9):1585-1594.

[5] HINTON G E,SALAKHUTDINOV R R.Reducing the dimensionality of data with neural networks.Science,2006,313:504 -507.

[6] DONG Y,LI D.Deep Learning and Its Applications to Signal and Information Processing[Exploratory DSP].IEEE Signal Processing Magazine,2011,28(1):145-154.

[7] LANGKVIST M,KARLSSON L,LOUTFI A.A review of unsuper- vised feature learning and deep learning for time-series modeling.Pattern Recognition Letters,2014,42:11-24.

[8] HUANG G B,ZHU Q Y,SIEW C K．Extreme learning machine:theory and applications.Neurocomputing,2006,70(1):489-501.

[9] 孙志军,薛磊,许阳明,等.深度学习研究综述.计算机应用研究,2012,29(8):2806-2810.

[10] BENGIO Y,LAMBIN P,POPOVICI D,et al.Greedy layer-wise training of deep networks.20th Annual Conference on Neural Information Processing System,Vancouver,2006.

[11] HINTON G E,OSINDERO S,TEH Y W.A fast learning algorithm for deep belief nets.Neural Computation,2006,18(7):1527-1554.

[12] PALM R B.Prediction as a candidate for learning deep hierarchical models of data．Denmark:Technical University of Denmark,2012.

[13] 骆晨钟,邵惠鹤.软仪表技术及其工业应用.仪表技术与传感器,1999(1):32-39.

Soft Sensor for Ball Mill Fill Level Based on DBN-ELM Model

KANG Yan,LU Mu-chao,YAN Gao-wei

(College of Information Engineering,Taiyuan University of Technology,Taiyuan 030024,China)

To solve the issue of low accuracy and weak stability of the traditional measurement method of ball mill fill level,a novel approach based on deep belief network and extreme learning machine was proposed.The vibration signal of ball mill bearing was selected as the instrumental variable.Deep belief network was employed to extract effective features from the power spectrum of vibration signal.Then effective features were put to the learning machine to proceed model training to obtain the soft sensor model.Lastly,the experiments were carried out on the lab-scale ball mill to validate the proposed method.The results show that the proposed method is more accuracy and stable than the traditional method.

ball mill fill level; deep belief network; feature extraction; extreme learning machine; soft sensor

山西省自然科学基金项目(2011011012-2)；国家863项目(2013AA102306)

2014-03-08 收修改稿日期：2014-11-02

TP29

A

1002-1841(2015)04-0073-03

康岩(1989—),硕士研究生,主要从事软测量及传感器信息融合研究。E-mail:yan2274@163.com