分布式相参射频探测系统信号积累方法综述

董华安，王建国

（1.电子科技大学，成都 611731；2.中国电子科学研究院，北京 100041）

分布式相参射频探测系统信号积累方法综述

董华安1，2，王建国1

（1.电子科技大学，成都 611731；2.中国电子科学研究院，北京 100041）

分布式相参射频探测系统要求对信号进行长时间积累。信号长时间积累带来的问题主要有跨距离单元走动、跨多普勒单元走动、跨波束走动以及由目标姿态角变化造成的回波散射矢量变化大等，使得信号积累效果变差。概述了分布式相参射频探测系统的产生背景、概念和面临的信号长时间积累问题，以及信号长时间积累方法、研究现状等，详细探讨了信号长时间积累的研究方向。

分布式相参射频探测系统；信噪比；信号积累；DBT；TBD

0 引 言

近十年来，随着射频探测理论研究和技术的蓬勃发展，出现了诸如分布式感知［1］、多入多出技术［2-3］、波形分集［4-6］、宽带天线、数字射频、基于知识的自适应信号处理［7-9］、嵌入式通信等各种先进的技术和概念。而近年来电子技术，特别是数字技术、计算机技术和网络技术的高速发展，也为此方面技术的实际应用奠定了基础。需求的牵引和技术的发展使得射频探测系统的研究进入了一个崭新的阶段，开始关注新的探测概念和理论的研究［10-12］。其中，对分布式探测系统的研究已成各国专家学者关注的重点。分布式系统可打破相控阵半个波长的布阵约束，实现灵活布阵，同时系统采用波形分集技术，可增加系统处理自由度［13］，提高系统在复杂环境下的探测、跟踪和识别性能［13-19］。但是要实现探测，必须对分布式系统进行相参处理，这是当前分布式探测系统研究的重大理论问题和发展趋势。当前天线技术、海量数据存储技术、高速数字信号处理技术、宽带通信技术的迅速发展，已经为分布式系统的实际应用提供了良好的技术条件。

分布式相参射频探测系统就是在这种背景下提出的。分布式相参射频探测系统采用正交凝视的探测模式，形成均匀分布的宽探测视场，使得相同积累时间下回波信噪比远低于相控阵体制，所以需要对回波信号进行长时间积累。然而长时间积累会带来跨距离单元走动、跨多普勒单元走动、跨波束走动以及目标姿态角变化造成的回波散射矢量变化等问题，使得信号长时间积累的效果变差。因此，如何实现信号长时间积累成为分布式相参射频探测系统面临的关键问题之一。

本研究安排如下：首先介绍分布式相参射频探测系统与信号长时间积累问题，接下来阐述信号长时间积累方法的研究现状，然后探讨信号长时间积累方法的研究方向，最后总结全文。

1 分布式相参射频探测系统与信号长时间积累问题

1.1 分布式相参射频探测系统

分布式相参射频探测系统（以下简称“分布式体制”）是指利用空间分布的多个射频单元组成相参系统，协同探测某指定区域，并将多个接收端获得的信号进行相参信号级融合处理，以获取更优的检测、估计、识别等系统性能［2，13-19］。

以上所提及的相参信号级融合处理即多接收端回波相参积累。信号检测和参数估计是探测系统的两个基本问题，对分布式体制也是如此，而且信号检测较参数估计更为重要，因为判断目标有无是参数估计的前提。噪声下的信号检测问题主要是通过积累信号能量提高信噪比。对于分布式体制，只有将多个接收天线的对同一目标的回波信号进行相参积累，才能获得最佳的信号检测性能。对于分布式体制而言，要求目标的回波信号满足一定程度的相关性要求。

对于分布式体制，在目标情况未知的条件下，为实现系统的最佳探测能力，可采用发射正交信号（相关系数为零）的工作方式［2-3，20-22］，形成均匀分布的宽探测视场。此时目标始终处在系统辐射的电磁场能量的包围中，此时，探测模式将发生本质变化，即从常规雷达的扫描模式演变为分布式体制下的凝视模式。

1.2 信号长时间积累

图1 分布式体制雷达信号层处理基本流程及相关问题

分布式体制雷达信号层处理基本流程［2，23］如图1所示。分布式体制发射正交信号；在目标处发生散射；接收机接收回波后用匹配滤波器进行信号分离，该过程完成了快时间维的相参积累；之后进行接收端波束形成［2，24］，完成空间采样维的信号积累；再进行脉冲积累，完成慢时间维的相参积累；然后进行包络检波和门限检测。雷达回波数据存储矩阵总体模型［25］如图2所示，其中，匹配滤波、接收端波束形成、脉冲相参积累都是线性处理，理论上处理顺序可以互换，但是会造成具体信号积累算法和计算量等的变化。

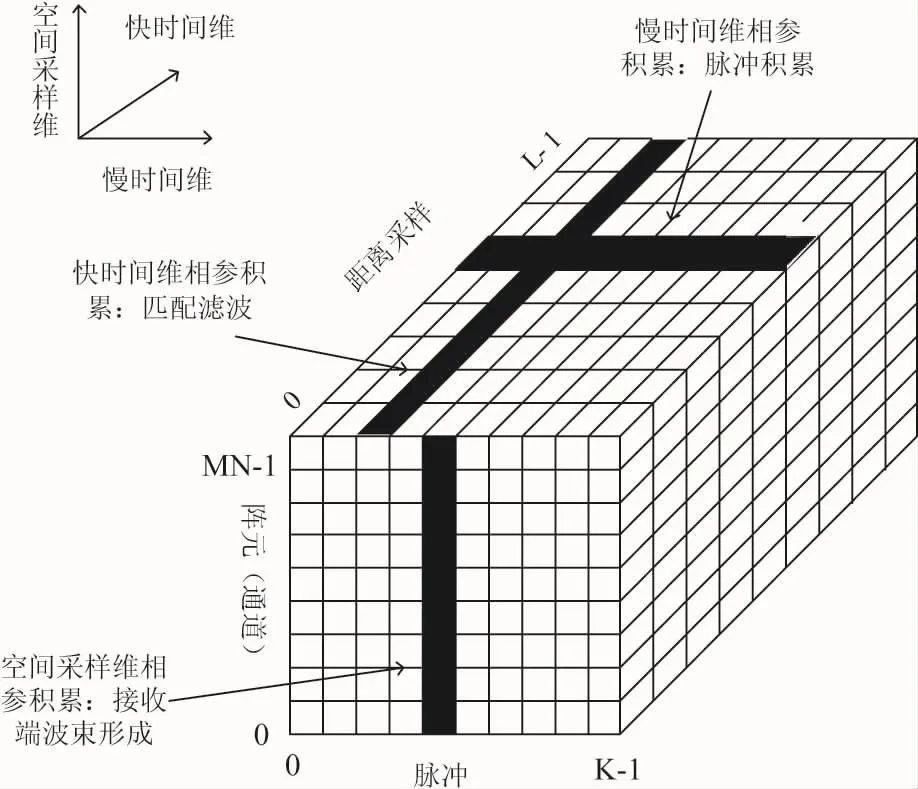
图2 雷达回波数据存储矩阵总体模型

假设阵元为M发N收，相控阵体制接收端共有N个接收通道，而分布式体制接收端用匹配滤波器进行信号分离后共有MN个通道。相同积累时间下，分布式体制噪声总功率是相控阵体制的M倍，回波信号总增益与相控阵体制相同，所以分布式体制总的信噪比为相控阵体制的。以某型机载预警雷达为例，该雷达采用相控阵体制，收发阵元数都为1000个量级，回波信号积累时间为10 ms量级。若采用分布式体制，相同积累时间下，回波信号总信噪比为相控阵体制的。为达到相同的检测性能，分布式体制需要对信号进行长时间积累来提高信噪比，从而使得积累时间从相控阵体制的10 ms量级上升到1 s量级甚至更长。若再延长回波信号积累时间，则可以大大增强雷达的探测威力，有望实现对以F22为代表的隐身目标进行反隐身。但是对信号进行长时间积累会带来很多问题，从而严重影响信号积累信噪比增益，如图1所示。这些问题主要由目标的复杂运动造成，主要问题包括跨距离单元走动、跨多普勒单元走动、跨波束走动以及目标姿态角变化造成的回波散射矢量变化等［26-34］，使得接收端匹配滤波器失配［35-36］、阵元间信号变化大、脉冲相参积累效果变差［26-34］。

事实上目标往往是非合作的，探测区域是否存在目标以及目标如何运动无法预先知道，因而对由目标运动造成的影响进行有效补偿非常困难，这对分布式体制能否实现构成了严峻挑战。所以，匹配滤波器如何设计、接收端如何波束形成、脉冲如何积累成为分布式体制面临的关键问题。

现主要探讨分布式体制下脉冲如何积累的问题。

2 信号长时间积累方法研究现状

2.1 基本积累方法

脉冲积累方法有相参积累［24］和非相参积累［24］。相参积累是指信号积累在包络检波之前完成，信号具有相位信息。相参积累的本质是各信号相同时刻点的复数相加，其定义与信号是否相参无关。针对信号相参这一理想情况，高斯白噪声背景下N个信号相参积累的信噪比增益为N［24］。非相参积累是指信号积累在包络检波之后完成，信号没有相位信息。非相参积累的本质是相同时刻点的包络相加，其定义与信号是否相参无关。非相参积累由于没有利用信号的相位信息，信号积累效果不如相参积累。高斯白噪声背景下非起伏目标的N个回波信号进行非相参积累，当回波数N很小时（N＝2或3），非相参积累增益比N0.8稍好［24］。随着N的增大，N的有效指数慢慢减小。当N很大时，信噪比增益最终慢慢趋近于。非相参积累对单个脉冲信噪比有一定要求，仿真条件下一般需大于0 dB，当回波信噪比过低时，积累效果急剧变差。分布式体制下，积累脉冲数在1 000甚至10 000量级，且单个回波脉冲信噪比远低于0 dB，对回波进行非相参积累的效果非常差。所以在分布式体制下单纯地进行非相参积累并不是理想的选择。

从雷达信号检测与跟踪算法的角度来看，脉冲积累方法也可以划分为先检测后跟踪（Detect Before Track，DBT）［37-42］和检测前跟踪（Track Before Detect，TBD）［37-46］。DBT是指在对目标进行航迹处理之前进行脉冲积累和门限检测。TBD是指在检测之前先采用一些跟踪算法估计目标在空间平面中的位置，然后用序列检测算法对估计的航迹进行检测判决，以实现弱小目标的能量沿其航迹积累的效果，从而提高检测性能。DBT和TBD中脉冲积累方法都可以采用相参积累或非相参积累，也可以将相参积累和非相参积累混合使用。DBT方法和TBD方法的实质都是用时间换取信噪比。

相参积累、非相参积累、DBT、TBD的关系见表1。

表1 4种脉冲积累方法的关系

2.2 脉冲积累方法研究现状

下面将从DBT和TBD分类的角度来对脉冲积累的研究现状进行阐述。

2.2.1 DBT研究现状

目前信号长时间积累算法以相参积累DBT和非相参积累DBT为主。

信号间相关系数为1时信号相参，信号在时域处处同相。当目标运动时，回波信号可能会发生跨距离单元走动。当目标加速度不为零时，回波信号可能会发生跨多普勒单元走动。目前对相参积累DBT方法的研究主要集中在距离走动补偿和多普勒走动补偿上。

距离走动产生的机理是距离的变化，即目标的径向移动，使得不同的脉冲回波位于不同的距离单元，因而可以结合回波信号和目标运动轨迹来做研究。距离走动补偿算法有Keystone变换法、包络插值移位补偿法、基于运动方程的积累方法等。

Keystone变换［47-52］是合成孔径雷达（Synthetic Aperture Radar，SAR）领域常用的一种距离走动补偿技术，通过对快时间维变换为频域的二维回波数据进行慢时间维的尺度伸缩，使变换后的匀速直线运动目标回波信号的多普勒频率与波形延迟解耦合，来完成距离走动补偿。但是基于Keystone变换方法的假设条件过于理想，只能用于目标作径向匀速直线运动这一特殊情形。

包络插值方法［47，49］则建立在有目标精确运动速度先验信息的基础上，当先验信息与目标真实速度匹配时，距离走动被补偿。

基于运动方程的方法［47，53］则直接从相参积累的本质，即回波信号相位对齐出发，将回波相位与反映目标运动状态的运动方程联系起来，通过目标运动方程对回波相位进行估计，再根据估计出来的相位对匹配滤波器进行设计，以匹配滤波方式实现相参积累。基于运动方程的长时间能量积累方法是对匹配滤波思想的延伸，其本质是对基于走动补偿类的相参积累算法的总结与概括，具有一定的概念意义。其实现途径仍然是补偿由于目标运动引起的距离走动与多普勒走动，以达到信号相参，与走动补偿类的相参积累算法不同之处在于，基于运动方程的长时间积累方法补偿的是回波对于发射信号的距离走动与多普勒走动，而传统的走动补偿类相参积累算法补偿的是回波相对于参考回波的相对距离走动与多普勒走动。基于运动方程的长时间能量积累方法仍然无法回避对目标运动先验信息的依赖。

多普勒走动的产生机理是径向速度的变化，即目标加速度不为零。因而对多普勒走动的分析也可以结合回波信号和目标的运动轨迹来研究。对目标与雷达之间的距离R（t）进行泰勒展开即可实现这种思路，能够定量分析各阶项对目标运动轨迹的影响，进而将这种影响映射到回波信号中来完成多普勒走动补偿。

多普勒走动补偿算法有解线性调频方法［47，54］、Wigner-Vill分布积分方法［47］等。径向匀加速直线运动以及进入角较大的斜向匀速直线运动的多普勒发生了线性走动，直接进行脉冲多普勒处理会造成脉冲能量在不同速度门间泄露，引起积累损失。解线性调频方法首先根据目标的运动特性确定加速度的范围并量化为K个离散值通过搜索方法进行多普勒处理，当量化后的加速度值与目标真实加速度多普勒吻合时，目标多普勒被补偿。Wigner-Vill分布积分方法和解线性调频方法是等价的。以上多普勒走动补偿算法仍然是建立在对目标运动状态的理想假设之上。

对非相参积累DBT方法也有相关的研究。如将Hough变换［47，55-56］用于非相参积累，其基本思想是将位于数据空间中的直线利用数学方法变换至参数空间，在参数空间中，直线上所有点形成一簇曲线并相交于直线的特征值点形成积累，噪声点或孤立点由于其随机性，没有特征值点，积累很小。Hough变换以此改善了信噪比，提高了检测性能。Hough变换检测直线图像的原理可以推广至曲线，此时曲线有更高维度的特征值点。推广了的Hough变换算法可以检测参数空间中任意复杂形状的曲线。对非相参积累的研究更多地体现在TBD算法中。

2.2.2 TBD研究现状

TBD方法的优点是能实现对目标运动轨迹的搜索，从而克服DBT方法对目标运动先验信息依赖的不足。此外，TBD的一个特点是计算量大。

目前绝大部分TBD文献都在研究基于帧间非相参积累的跟踪算法，如动态规划［37-46］、粒子滤波［37-46］，而忽略了对检测部分的研究，多数文献甚至认为TBD的本质就是非相参积累，对基于帧间相参积累的TBD算法研究较少。原因在于相控阵体制采用扫描探测模式，帧间数据有较长的时间间隔，帧间数据相参性较差。

对相参积累TBD［57-60］的研究较少，文献［58］研究了基于动态规划的帧间相参积累算法，在对目标进行跟踪时采用Keystone变换对距离走动进行校正。该方法无法进行长时间的积累，且对信噪比有一定要求，当信噪比低于2 dB时无法检测到目标。文献［59］研究了基于粒子滤波的帧间相参积累算法，在对目标进行跟踪时采用帧间相参积累方法，对单帧信噪比要求可降低至-5 dB，且能进行0.5 s量级的长时间积累，具备实现更低信噪比条件下1s量级以上长时间积累的潜力。

当前对相参积累TBD的研究较少，主要表现有：（1）都是在相控阵体制下完成，帧数据获取方式与分布式体制不同，单个脉冲信噪比仍远高于分布式体制；（2）只涉及初步的研究，在高斯白噪声背景，对运动状态为径向匀速直线运动和径向匀加速直线运动的单目标进行相参积累TBD处理；（3）帧数据较少，未尚达到长时间积累的要求。

3 未来研究方向探讨

本研究从以下两个角度来探讨分布式体制下信号长时间积累的研究方向。

角度1：将搜索的思想彻底化：轨迹，速度，加速度，幅度等。

角度2：雷达信号空间处理维度发展和信号检测与跟踪算法。

3.1 搜索思想

当回波信号积累时间较短时，由于回波信号之间具有良好的相参性，信号直接积累即可。当信号积累时间较长时，在DBT方法中，信号积累算法可以对目标运动速度和加速度进行搜索，并采用信号积累效果最好的速度-加速度组合来描述目标运动状态。然而不足是，DBT方法在进行长时间积累时一般都需要假设目标运动形式，即目标作径向匀速直线运动或径向匀加速直线运动。事实上，既不知道探测区域是否存在目标，即使存在目标，也不知道目标的运动形式。即使目标作径向匀速直线运动或径向匀加速直线运动的假设是合理的，目标的位置仍然是未知的。因此，如果要在实际中使用DBT方法进行信号长时间积累，那么需要对目标位置进行搜索，而这种搜索方式将带来巨大的计算量，从本质上讲这是用穷举法来实现的TBD，而采用穷举法恰恰是TBD要避免的。

从信号长时间积累本身所面临的问题来看，发展趋势是将搜索的思想彻底化，对目标的位置、速度、加速度和幅度等信息进行搜索，而在实现搜索的过程中，又要避免使用穷举法以免带来巨大的计算量。

TBD将搜索的思想彻底化了。但目前TBD的不足是，由于帧间数据相参性较差，绝大部分公开发表的文献直接默认帧间积累为无走动校正的非相参积累，对信号检测部分关注较少。与传统TBD不同的是，分布式体制下TBD中单帧信噪比远低于相控阵体制，使用非相参积累的效果非常差，因此无法使用传统TBD中帧间非相参积累方法。且分布式体制下TBD必须面对长时间积累造成的走动问题，若不进行走动校正，帧间数据有效积累时间将很短。

因此，为了应对分布式体制下单个回波信噪比过低的问题，需要发展基于帧间相参积累的TBD。单个回波信噪比越低，所需的信号有效积累时间就越长，在基于帧间相参积累的TBD中进行有效地走动校正也是必要的。

3.2 信号空间维度和检测与跟踪算法

信号检测的本质是模式识别，通过利用目标与背景之间的差异性特征来检测目标的有无，信号空间维度越高，这种可利用的差异性特征就越多。

在雷达信号检测中，背景主要有杂波、人为干扰和噪声等，杂波和人为干扰可以采用相应算法来抑制，而噪声是电路所固有的，分布于信号带宽中的每一个频点，无法消除，应对噪声的所有方法本质上都是通过提高信号能量来提高信噪比，从而改善信号检测性能。

在雷达系统中，为应对杂波、人为干扰和噪声等背景，信号检测与跟踪算法的信号空间维度呈现由低向高演化的趋势［12］，从而利用高维空间中目标与背景之间更大的差异性特征，提高复杂背景中对弱目标检测的能力。信号检测与跟踪算法信号空间处理维度增加的表现是，信号空间由早期的时域1维检测，已经演化出时-频域2维检测（动目标显示MTI、动目标检测MTD、脉冲多普勒PD等）和先检测后跟踪（DBT），正进一步向距离-方位-信号采集周期构成的3维检测前跟踪（TBD）演变。可以预期，未来还可能向更高维的检测与跟踪算法方向发展，如图3所示。

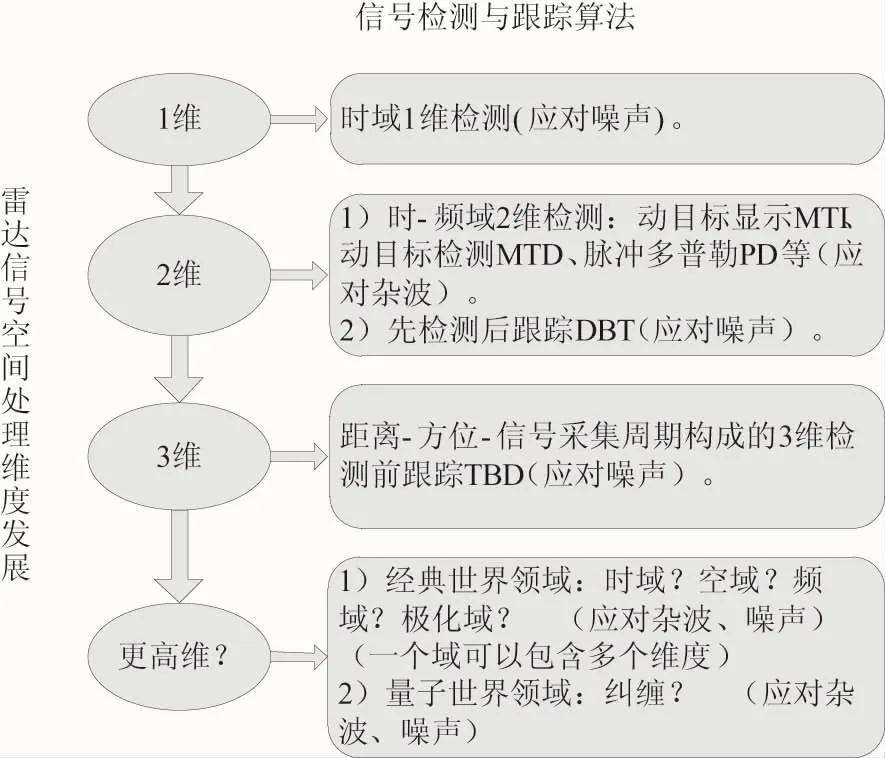
图3 雷达信号空间处理维度发展和信号检测与跟踪算法

信号积累的发展趋势是要对信号进行长时间积累，因此，有别于传统的信号积累方法，TBD将信号采集周期作为一个单独的信号空间维度，达到用时间换取空间的目的，从而可以对目标轨迹进行搜索，并沿其轨迹进行信号的长时间积累，其本质是利用时间这一维度带来的信号与背景之间的差异性特征。因此，在信号长时间积累中，TBD是优于DBT的发展方向。此外，从信号处理和数据处理的顺序来看，时间作为一个单独的信号空间维度使得信号处理和数据处理将不再有明显的先后顺序之分。

4 结 语

信号长时间积累问题是分布式体制面临的关键问题之一，目前该问题仍然没有得到较好的解决。本研究在对分布式体制产生背景及其概念和所面对的问题进行论述的基础上，结合信号长时间积累方法的研究现状，认为后续研究应当从搜索思想和信号空间维度发展上来把握方向。此外，单个脉冲信噪比要求分析、信号有效积累时间分析、信号长时间积累中的检测器设计和杂波抑制等问题也是信号长时间积累的重要研究方向。

［1］WICKSM C，MOOREW.Distributed and Layered Sensing［C］.Waveform Diversity and Design Conference，2007.International.IEEE，2007：233-239.

［2］LI J，STOICA P.MIMO Radar with Colocated Antennas［J］.Signal Processing Magazine，IEEE，2007，24（5）：106-114.

［3］FISHLER E，HAIMOVICH A，BLUM R，et al.MIMO Radar：An IdeaWhose Time Has Come［C］.Radar Conference，2004.Proceedings of the IEEE.IEEE，2004：71-78.

［4］CAPRARO G T，BRADARIC I，WICKSM C.Waveform Diversity and Electromagnetic Compatibility［C］.Electromagnetic Compatibility，2007.EMC 2007.IEEE International Symposium on.IEEE，2007：1-7.

［5］WICKSM C，ANTONIK P.Waveform Diversity in Intelligent Sensor Systems［C］.Waveform Diversity and Design in Communications，Radar and Sonar，2006.The Institution of Engineering and Technology Forum on. IET，2006：1-6.

［6］GARNHAM JW，ROMAN JR.Why and What isWaveform Diversity，and How Does it Affect Electromagnetics？［C］.Electromagnetic Compatibility，2007.EMC 2007. IEEE International Symposium on.IEEE，2007：1-5.

［7］HAYKIN S.Cognitive Radar：AWay of the Future［J］. Signal Processing Magazine，IEEE，2006，23（1）：30-40.

［8］GUERCIJR.Cognitive Radar：A Knowledge-aided Fully Adaptive Approach［C］.Radar Conference，2010 IEEE. IEEE，2010：1365-1370.

［9］GUERCI JR，GUERCIR M，RANAGASWAMY M，et al.CoFAR：Cognitive Fully Adaptive Radar［C］.Radar Conference，2014 IEEE.IEEE，2014：0984-0989.

［10］WIESBECK W.The Radar of the Future［C］.Radar Conference（EuRAD），2013 European.IEEE，2013：137-140.

［11］BROOKNER E.MIMO Radar Demystified and Where it Makes Sense to Use［C］.Radar Conference，2014 IEEE.IEEE，2014：0411-0416.

［12］杨建宇.雷达技术发展规律和宏观趋势分析［J］.雷达学报，2012，1（1）：19-27.

［13］BLISSDW，FORSYTHE KW.Multiple-input Multipleoutput（MIMO）Radar and Imaging：Degrees of Freedom and Resolution［C］.Signals，Systems and Computers，2004.Conference Record of the Thirty-Seventh Asilomar Conference on.IEEE，2003，1：54-59.

［14］FISHLER E，HAIMOVICH A，BLUM R S，etal.Spatial Diversity in Radars-models and Detection Performance［J］.Signal Processing，IEEE Transactions on，2006，54（3）：823-838.

［15］LEHMANN N H，HAIMOVICH A M，BLUM R S，etal. High Resolution Capabilities of MIMO Radar［C］.Signals，Systems and Computers，2006.ACSSC'06.Fortieth Asilomar Conference on.IEEE，2006：25-30.

［16］FISHLER E，HAIMOVICH A，BLUM R，etal.Performance ofMIMO Radar Systems：Advantages of Angular Diversity［C］.Signals，Systems and Computers，2004. Conference Record of the Thirty-Eighth Asilomar Conference on.IEEE，2004，1：305-309.

［17］HE Q，BLUM R S.Performance and Complexity Issues in Noncoherentand CoherentMIMO Radar［C］.Signals，Systems and Computers，2009 Conference Record of the Forty-Third Asilomar Conference on.IEEE，2009：1206-1210.

［18］LI J，STOICA P.MIMO Radar Signal Processing［M］. Hoboken，NJ：J.Wiley＆Sons，2009：10-20.

［19］HALEEM M A，HAIMOVICH A.Range and Speed Resolution in Coherent Distributed MIMO radar with Gaussian Pulse Trains［C］.Information Sciences and Systems，2009.CISS 2009.43rd Annual Conference on.IEEE，2009：114-117.

［20］CATTENOZM，MARCOSS.Adaptive Processing forMIMO Radar Realistic non Perfectly Orthogonal Waveforms［C］.Radar Conference，2014 IEEE.IEEE，2014：1323-1328.

［21］GALATIG，PAVAN G.Waveforms Design for Modern and MIMO Radar［C］.EUROCON，2013 IEEE.IEEE，2013：508-513.

［22］STOICA P，LI J，XIE Y.On Probing Signal Design for MIMO Radar［J］.Signal Processing，IEEE Transactions on，2007，55（8）：4151-4161.

［23］FUHRMANN D R.MIMO Radar Signal Processing for Distributed Phased Arrays［C］.Computational Advances in Multi-Sensor Adaptive Processing（CAMSAP），2011 4th IEEE InternationalWorkshop on.IEEE，2011：1-4.

［24］FRIEDLANDER B.On Transmit Beamforming for MIMO Radar［J］.Aerospace and Electronic Systems，IEEE Transactions on，2012，48（4）：3376-3388.

［25］RICHARDSM A.雷达信号处理基础［M］.北京：电子工业出版社，2008：86-87，240-253.

［26］ZHEN J，SHU L W，XIAN J X.Signal Coherent Processing Methods of MIMO Radar Based on RFT［J］. 2013.

［27］LUO C，LIJ，LIU H M，et al.Compensation Method for Envelop Migration of MIMO Radar High Speed Moving Target Based on Transmit Signal Pre-process［C］.Microwave and MillimeterWave Circuits and System Technology（MMWCST），2012 International Workshop on. IEEE，2012：1-4.

［28］SAMMARTINO P F，TARCHID，Fortuny-Guasch J，et al.Phase Compensation and Processing in Multiple-input-multiple-output Radars［J］.IET Radar，Sonar＆Navigation，2012，6（4）：222-232.

［29］MOO PW.Range-doppler Migration in Coherent MIMO Radar［C］.Radar Conference（EuRAD），2011 European.IEEE，2011：138-141.

［30］MOO PW.Multiple-input Multiple-output Radar Search Strategies for High-velocity Targets［J］.IET radar，sonar＆navigation，2011，5（3）：256-265.

［31］YANG Y，BLUM R S.Phase Synchronization for Coherent MIMO Radar：Algorithms and Their Analysis［J］. Signal Processing，IEEE Transactions on，2011，59（11）：5538-5557.

［32］YANG Y，BLUM R S.Some Phase Synchronization Algorithms for Coherent MIMO Radar［C］.Information Sciences and Systems（CISS），2011 45th Annual Conference on.IEEE，2011：1-6.

［33］MAOW X，ZHANG Z，LIX R.Ubiquitous MIMO Radar Energy Integration Detection Based on Range Synthesis［C］.Radar（Radar），2011 IEEE CIE International Conference on.IEEE，2011，2：1760-1763.

［34］LIC，LIU H，LI J，et al.Parameter Selection of MIMO Radar Under the Long Time Integration［C］.Intelligent Signal Processing and Communication Systems（ISPACS），2010 International Symposium on.IEEE，2010：1-4.

［35］XUN F，SHOU Y W，PENG F D，et al.MIMO Radar Signal Separation Algorithm in Non-Gaussian clutter［C］. Radar（Radar），2011 IEEE CIE International Conference on.IEEE，2011，2：979-983.

［36］HU L，LIU H，FENG D Z，et al.Optimal Mismatched Filter Bank Design forMIMORadar via Convex Optimization［C］.Waveform Diversity and Design Conference（WDD），2010 International.IEEE，2010：000126-000131.

［37］易伟.基于检测前跟踪技术的多目标跟踪算法研究［D］.成都：电子科技大学，2012：1-4.

［38］龚亚信.基于粒子滤波的弱目标检测前跟踪算法研究［D］.长沙：国防科学技术大学研究生院，2009：1-9.

［39］吴兆平.雷达微弱目标检测和跟踪方法研究［D］.西安：西安电子科技大学，2012：1-10.

［40］林再平.天基红外图像弱目标检测前跟踪技术研究［D］.长沙：国防科学技术大学，2012：1-8.

［41］吴孙勇.天基预警雷达微弱动目标检测与定位方法研究［D］.西安：西安电子科技大学电子工程学院，2011：1-10.

［42］樊玲.微弱目标检测前跟踪算法研究［D］.成都：电子科技大学，2013：1-5.

［43］SAMUEL JD，MARK G R，BRIAN C.A Comparison of Detection Performance for Several Track-before-detect Algorithms［J］.EURASIP Journal on Advances in Signal Processing，2007：22-37.

［44］BARNIV Y，KELLA O.Dynamic Programming Solution for Detecting Dim Moving Targets Part II：Analysis［J］. Aerospace and Electronic Systems，IEEE Transactions on，1987（6）：776-788.

［45］BARNIV Y.Dynamic Programming Solution for Detecting Dim Moving Targets［J］.Aerospace and Electronic Systems，IEEE Transactions on，1985（1）：144-156.

［46］DAVEY S J，RUTTEN M G.A Comparison of Three Algorithms for Tracking Dim Targets［C］.Information，Decision and Control，2007.IDC'07.IEEE，2007：342-347.

［47］周成义.基于分布式相参射频探测系统的长时间能量积累方法研究［D］.成都：电子科技大学，2012：19-51.

［48］李春林，吴琳拥.基于Keystone变换的长时间相参积累研究［J］.电子科技，2013，26（6）：148-152.

［49］夏卓卿，陆军，陈伟建.脉冲多普勒雷达长时间积累技术研究［D］.成都：电子科技大学，2010：14-38.

［50］张月，邹江威，陈曾平.泛探雷达长时间相参积累目标检测方法研究［J］.长沙：国防科技大学学报，2010，32（6）：15-20.

［51］夏卓卿，陆军，陈伟建.凝视动目标相参积累技术研究［J］.中国电子科学研究院学报，2009，4（5）：498-502.

［52］张顺生，曾涛.基于 Keystone变换的微弱目标检测［J］.电子学报，2006，33（9）：1675-1678.

［53］周成义，毛五星，陆军，等.基于运动方程长时间能量积累方法的实现［J］.中国电子科学研究院学报，2012，7（1）：58-62.

［54］吴兆平，何学辉，苏涛.带有距离走动和多普勒扩散的高速运动目标检测［J］.哈尔滨工程大学学报，2010，31（4）：476-480.

［55］吴兆平，苏涛.采用目标轨迹积累的窄带雷达信号长时间积累方法［J］.电路与系统学报，2012，17（2）：6-12.

［56］庞存锁，侯慧玲，韩焱.基于霍夫变换的高速微弱目标检测算法［J］.电子与信息学报，2012，34（3）：754-757.

［57］JIAN X B，JUN W.Weak Target Detection Using Dynamic Programming TBD in CDMA Based Passive Radar［C］.Radar Conference，2009 IET International.IET，2009：1-4.

［58］KUN W，XIAO L Z.A TBD Method Using Multi-frame Coherent Integration［C］.Synthetic Aperture Radar（APSAR），2011 3rd International Asia-Pacific Conference on.IEEE，2011：1-4.

［59］RABASTE O，RICHéC，LEPOUTRE A.Long-time Coherent Integration for Low SNR Target via Particle Filter in Track-before-detect［C］.Information Fusion（FUSION），2012 15th International Conference on.IEEE，2012：127-134.

［60］XU J，YU J，PENG Y N，et al.Focus-before-detect for Radar Target Detection［C］.Radar（Radar），2011 IEEE CIE International Conference on.IEEE，2011，1：430-433.

董华安（1990—），男，电子科技大学硕士研究生，主要研究方向为分布式探测系统信号检测与跟踪技术；

E-mail：13552454708＠163.com

王建国（1954—），男，电子科技大学教授，电子工程系主任，主要研究方向为双基SAR成像技术、信息对抗、信息获取和目标识别。

Review of Signal Integration M ethods in Distributed Coherent RF Detection System

DONG Hua-an1，2，WANG Jian-guo1
（1.University of Electronic Science and Technology，Chengdu 611731，China；2.China Academy of Electronics and Information Technology，Beijing 100041，China）

Distributed coherent RF detection system（DCRFDS）requires long-time signal integration. However，long-time signal integration brings problems such as rangemigration，Dopplermigration，beam migration，and the change of echo scattering vectormainly caused by the change of target attitude angle，allwhich will lead to aworse resultof signal integration.The background，concept，long-time signal integration problem，and methods and research status of long-time signal integration of DCRFDS are introduced.Also，the research direction in long-time integration field is discussed in detail.

DCRFDS；SNR；signal integration；DBT；TBD

TN957.51

：A

：1673-5692（2015）01-017-08

10.3969／j.issn.1673-5692.2015.01.003

2014-12-05

2015-01-16

国家安全重大基础研究项目