新型油船操纵运动数值模拟
邱云明,程文才,黄志清
(镇江船艇学院,江苏镇江 212003)
新型油船操纵运动数值模拟
邱云明,程文才,黄志清
(镇江船艇学院,江苏镇江 212003)
新船艇在制造之前要进行操纵性预报,而数值模拟现成为预报中一种较可靠方法。为了研究一艘新型万吨油船的操纵性,采用分离性数学模型(MMG),结合船艇粘性水动力性能特点,构建船艇操纵运动模拟模型,运用4阶龙格-库塔(Runge-Kutta)数值方法求解该微分方程。基于该综合集成方法,对该新油船在满载条件下的定常回转试验、Z形试验等自航模操纵运动进行数值模拟,并将数值模拟结果同该船的自航模试验进行比较,模拟结果与试验数值较吻合。研究表明,利用文中的数值模拟法可以有效实现该新油船操纵运动模拟和操纵性预报。
油船;数学模型;船艇;操纵运动;数值模拟
0 引言

船艇操纵运动数值模拟在船艇操纵性的预报船艇操纵器研制、船艇六自由度运动试验平台建设等方面发挥重要作用,其数值模拟精度如何,直接关系到操纵性预报的真实性、操纵模拟器模拟的逼真度、船艇运动平台的检测、试验的可靠性。目前,许多国家要求在船舶设计的初始阶段对新研制船的操纵性进行预报,并提交操纵性计算书和相关试验报告。随着计算机能力的不断增强,逐步成熟的数值模拟技术为船艇操纵性预报、船艇高精度模拟运动提供了有效手段。
1 操纵运动模型
船艇操纵运动模拟数学模型主要有整体型和MMG分离型。由于MMG模型物理意义明确,在工程应用上较广泛。应用MMG模型进行运动模拟时,其精度主要在于水动力导数的获取。在大地坐标系和随船运动坐标系下,采用MMG分离建模的思想建立船艇操纵运动方程,文中假定船艇船体为刚体,航行在无限深广水域,忽略船体摇荡的影响,数值模拟时采用的坐标系原点与船艇重心重合,无因次船艇操纵运动微分方程为[1]:
式中:各参数均为无因次化,“'”表示无因次符号;m'为船艇质量;m'x、m'y分别为在水中运动时沿着OX、OY轴方向的附加质量;u'、v'分别为船艇纵向和横向速度;˙u'、˙v'分别为船艇纵向和横向加速度;r'为船艇绕OZ轴的旋转角速度;˙r'为船艇绕OZ轴的旋转角加速度;I'zz为船艇质量绕OZ轴的转动惯量;J'zz为船体在水中运动时自身绕OZ轴的附加质量惯性矩;X'H、Y'H、N'H分别为船体产生的纵向水动力、横向水动力和力矩;X'R、Y'R、N'R分别为舵产生的纵向水动力、横向水动力和力矩;X'P、Y'P、N'P分别为螺旋桨产生的纵向水动力、横向水动力和力矩;x'C为船艇重心在固定坐标系x轴上的坐标值。
1.1 附加质量和附加质量惯性矩
本文针对某29 000 t新型油船进行操纵性研究。根据油船的主要参数及其结构,采用以下回归公式计算 m'x、m'y、J'zz[2]。

式(2)~式(4)中:L、B、d、Cb分别为船长、船宽、吃水、方形系数。
1.2 船体粘性流体动力
目前船体粘性流体动力获取主要有试验和计算2种,其中计算获取的方法主要有CFD数值计算和估算模型。船艇的几种线性水动力导数和非线性水动力导数通过CFD数值计算,虽然比较精确,但建模较复杂,数值计算后进行后处理方法获取,耗时比近似模型要多。通过参考有关文献和本文研究,近似模型求水动力导数,要看具体船型,对于集装箱、油船、滚装船,可以采用贵岛模型[1—2],求出粘性流体动力X'H、Y'H和力矩N'H的非线性表达式:

为保证船艇操纵运动模拟和操纵性预报的精度,引入了一些非线性导数项,如 X'vv、X'vr、Y'vv,…。X'(u)的大小和该船无因次阻力相等。
对于线性水动力导数估算主要采用:

对于非线性导数 X'vv、X'rr为小量,忽略不计。X'vr约为横向附加质量的20%~50%,其大小为:X'vr=my(1.11Cb-1.07)。其他非线性水动力导数估算采用公式:

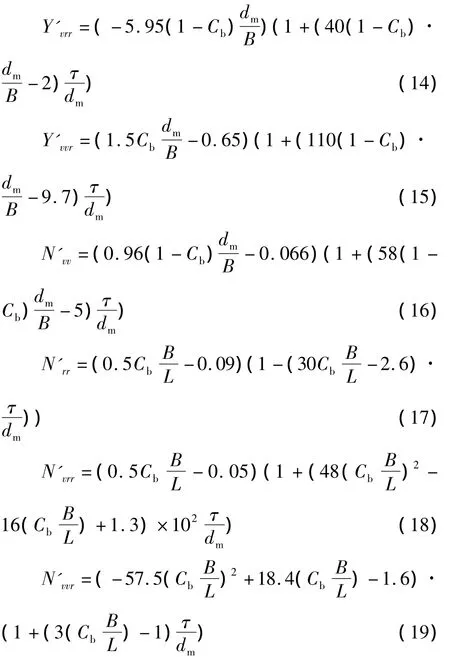
式中:dm为平均吃水,dm=(dA+dF)/2,dA为首吃水,dF为尾吃水,τ为吃水差,τ'为无量纲吃水差,τ'=(dA-dF)/dm;λ =2dm/L。
1.3 螺旋桨力及力矩
对于单桨船在旋回运动过程中,其螺旋桨的推力X及力矩[2]N大小,由下式进行计算:
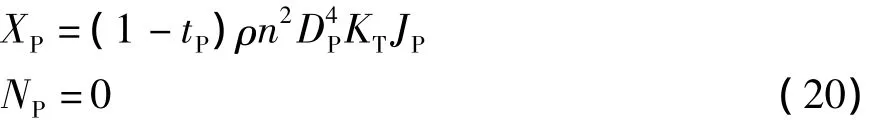
式中:XP为螺旋桨的推力;NP为螺旋桨的力矩;tP为螺旋桨推力减额分数;n为螺旋桨转速;DP为螺旋桨直径;KT为螺旋桨敞水推力系数;JP为螺旋桨进速系数,JP=u(1-wP)/nDP,其中,wP为船艇操纵运动过程中螺旋桨处的有效伴流分数,受运动幅度的影响,与直航时的wP0不同。可以将(1-wP)用式(21)表示:

式中:wP0为螺旋桨敞水伴流分数;β为船舶坐标原点处的漂角;l'P为试验系数,几乎与x'P一致;r'为无因次回转角速度;x'P为螺旋桨的无因次坐标;v'P为螺旋桨无因次进速。
1.4 舵力及力矩
由于舵位于螺旋桨的后面,其舵力受到螺旋桨旋转、船体伴流的影响,因此单个操舵引起的舵力及力矩[2]为:
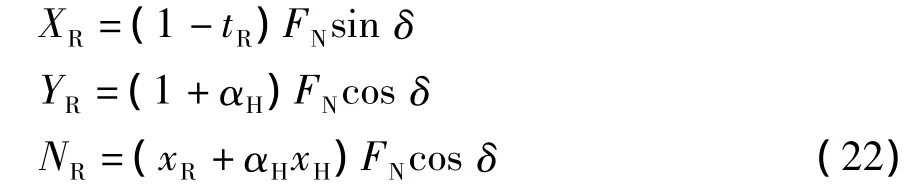
式中:δ为舵角;tR为舵力减额系数;αH为操舵引起的船体横向力的增额系数;xR为舵力作用中心的坐标;xH为操舵引起的船体增额横向力作用中心的坐标。tR、αH、xH分别表示:



式中:wR为船艇操纵运动过程中舵处的伴流分数,它受船运动幅度的影响,与直航时伴流分数wR0不一样,可由船艇的模型试验得到:wR=wR0wP/wP0;K为系数,当 δ≥0,K=1.065,当 δ<0,K=0.935,其中δ为舵角,正负号表示左、右舵;G(s)为螺旋桨尾流的加速效应的函数,G(s)可以表示为;

式中:k=0.6(1-wP)/(1-wR);s=1-(1-wP)u/nPP;η =DP/HR,PP、HR、DP分别表示为螺旋桨螺距、舵高、螺旋桨直径。
αR为水流对舵的有效冲角,其大小模型为:



2 操纵运动数值解法
在实际工程数值计算中,龙格-库塔数值方法是一种应用广泛的高精度单步算法,求解微分方程时具有精度高、收敛性、稳定性好特点,因此选用该方法求解操纵运动微分方程[3—4]。其MMG操纵运动微分方程组变形为:

式中:Δt为时间积分步长;ki、li、mi(i=1,2,3,4)为相互间有关联的系数,其大小在此省略。船艇运动的纵向速度、横向速度和转首角速度求得之后,继而求得船艇操纵运动轨迹。
3 数值模拟的试验验证
选取了某29 000 t新型油船为研究对象,试验船模的缩尺比为1:40。实船和模型的主要参数见表1,实船的桨舵主要参数见表2。其中,表中的LOA、LWL、LPP、B 、T、Cb分别表示总长、设计水线长、垂线间长、型宽、设计吃水、方型系数[5]。在船模操纵性试验中的初始速度为0.81 m/s。

表1 某新型油船实船及船模的主要参数
在研究中,运用C语言编程实现该船的回转运动、Z形运动2种操纵运动的数值模拟。在模拟时,选取舵角为15°、25°、35°船模定常回转运动中的定常直径的模拟值与试验值进行比较,见表3。其中,右舵35°的船模回转运动数值模拟轨迹与船模试验轨迹,如图1所示。Z形运动的数值模拟与试验比较结果见表4,其中选取10°/10°的Z形运动数值模拟与试验时的首向角变化轨迹进行比较。Z形运动数值模拟与船模试验比较如图2所示。

表2 某新型油船操纵设备的主要要素

表3 船模的数值模拟与船模试验定常回转直径比较
基于上述的数值模拟和试验的结果来看,数值模拟所得的直径值与试验所得的直径值相对误差在3.37%以下,可见数值模拟回转轨迹和试验回转轨迹基本吻合。

表4 Z形运动数值模拟与船模试验比较
从图2和表4可以看出:Z形运动中的第一超越角ψov1、第二超越角ψov2数值模拟值与船模试验值误差值在-2°~2°内,第三超越角ψov3误差5°左右,误差主要在于船模尺度效应和操舵滞后的影响。
4 结论
通过对操纵运动数值模拟与试验比较,本文所构建的操纵运动数学模型和操纵运动数值解法,对于预报此类新型油船的操纵运动和操纵性是可行的,能较好地满足工程的需要。数值模拟的精度主要取决于操纵运动模拟模型和水动力导数,不同船艇的水动力的导数是不同的。对于水动力导数的获取应针对船型选择合适的方法,只要满足工程精度,应尽可能选择快捷实用的计算方法;但是对于船型比较特殊的,如某些军用船艇,并且模拟精度要求高,其水动力导数建议用CFD方法获取。对于大风浪中船艇操纵运动模拟,方法相同,只要在操纵运动方程右边再加风力、风力作用力矩、波浪力及波浪的作用力矩。船艇操纵运动数值模拟技术在船艇操纵模拟器、船艇六自由度运动平台的研制和船艇操纵性预报、船艇设计优化中具有重要的经济价值和现实意义。
[1] 吴秀恒.船舶操纵性和耐波性(第2版)[M].北京:人民交通出版社,1999.
[2] 贾欣乐,杨盐生.船舶运动数学模型-机理建模与辨识建模[M].大连:大连海事大学出版社,1999.
[3] 张淋,王志东.船舶操纵性能预报浅水修正模型的对比研究[J].江苏船舶,2008,25(1):9-16.
[4] 范尚雍,朱军,程智斌.驱逐舰操纵性预报[J].中国造船,1990,31(1):3-8.
[5] 邱云明.受损船操纵性数值计算与试验研究及其综合评价[D].武汉:武汉理工大学,2011.
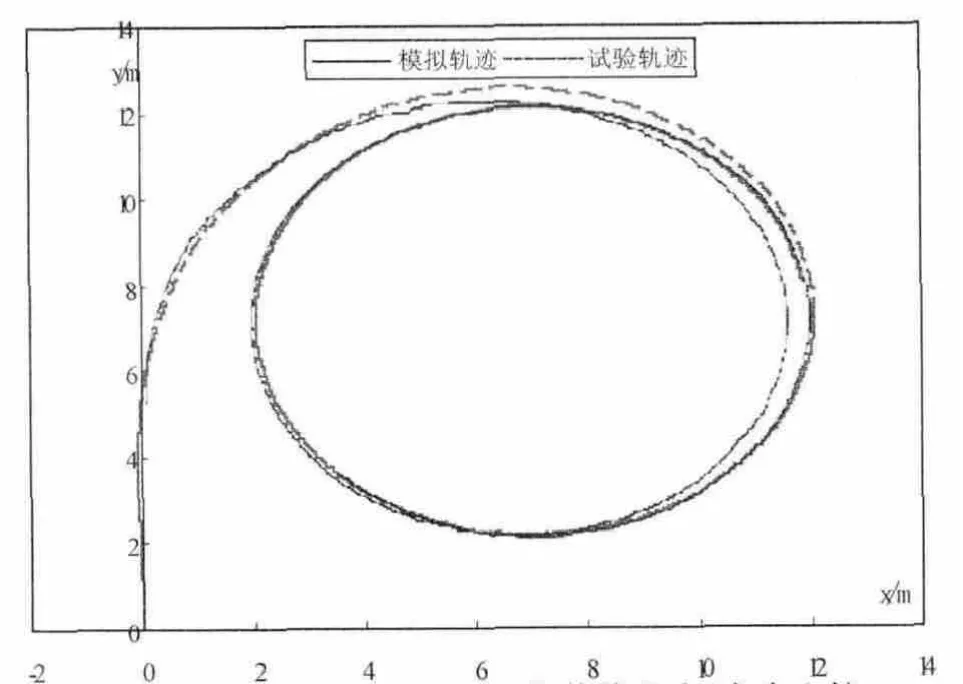
图1 右舵35°回转运动的数值模拟与试验比较

图2 Z形运动数值模拟与船模试验比较
The maneuverability will be predicted before the new ship type is manufactured,Numerical simulation is one of reliable methods in ship maneuverability prediction.In order to research a new type ten thousand ton oil tanker's maneuverability,a mathematical model for simulating the ship maneuvering motion was constructed adopting the separable mathematical model group(MMG)model,combining the viscous hydrodynamic characteristics of ship,four order Runge Kutta numerical method is used to solve differential equations of ship maneuvering motion.A maneuvering motion of stationary turning test and Zigzag test of the oil tanker's self-propulsion model in the condition of full-load displacement are numerical simulated respectively based on the comprehensive integration method,the numerical simulation results are in good agreement with the experimental values through comparing and analyzing with ship tests.The research shows that the numerical simulation researched in the paper can realize the simulation of new type oil tanker maneuvering motion and its maneuverability prediction.
Numerical simulation of new type oil tanker manipulation motion
Qiu Yunming,Cheng Wencai,Huang Zhiqing(5)
U661.33
A
全军后勤科研条件建设项目(后司[2011]109号)
2015-02-24
邱云明(1973—),男,副教授,博士,研究方向为船艇水动力及船艇操纵。

