基于图像压缩传感的光学单点成像系统

张 涛，钟舜聪，2，3，沈耀春，姚立纲

(1．福州大学机械工程及自动化学院无损检测实验室，福建福州 350108；2．华东理工大学承压系统安全科学教育部重点实验室，上海 200237；3．福建省医疗器械行业技术开发基地，福建福州 350000;4．英国利物浦大学电气电子工程系，英国)



基于图像压缩传感的光学单点成像系统

张 涛1，钟舜聪1，2，3，沈耀春4，姚立纲1

(1．福州大学机械工程及自动化学院无损检测实验室，福建福州 350108；2．华东理工大学承压系统安全科学教育部重点实验室，上海 200237；3．福建省医疗器械行业技术开发基地，福建福州 350000;4．英国利物浦大学电气电子工程系，英国)

压缩传感理论(Compressive Sensing，简称CS)以远低于奈奎斯特采样频率对稀疏信号进行全局观测，通过少量观测值即可准确重构原始信号，突破了香农采样定理的瓶颈，使得宽带信号和高分辨率信号的采集成为可能。目前压缩传感理论大都停留在理论研究和仿真阶段，鲜有涉及将该理论硬件化进行实践应用。文中介绍了最小均方差线性估计(MMSE)算法，通过与常用重构算法的仿真重构对比，突出了MMSE算法的优越性，证明了该算法在低采样率下重构质量较高，且具有较好的实践应用潜力。并进一步搭建了光学单点成像系统对压缩传感理论进行应用研究，实验表明该系统成像效果良好，具有较好的应用价值。

压缩传感；稀疏性；重构算法；最小均方差线性估计方法；成像系统

0 引言

在传统的信号处理过程中，信号先遵循采样定理进行数据采集，然后再将数据进行压缩[1]，在信号压缩的过程中浪费了大量的数据计算以及内存资源。信号带宽问题的不断出现，这给硬件设备带来了极大的挑战，使得宽带信号的处理变得日益困难[2]。

2004年，D．Donoho[3]、T．Tao[4]及E．Candes[5]等人提出了一种新型的信息处理理论，即压缩传感[3-7](Compressive Sensing，简称CS)，为解决上述问题提供了新的思路。

CS理论虽然目前处于研究的初始阶段，但发展迅速，已经发展了多种形式，例如Bayesian CS理论、1-BIT CS理论、无限维CS理论、分布CS理论、变形CS理论等，已经发展成为学术界的研究热点。

与采样定理的区别在于，压缩传感理论表明只要信号通过某种变换后可以稀疏表示，就能以较低的频率进行全局性采样，该采样频率可以远小于采样定理所要求的标准，从而获得少量的全局信号观测值，再通过重构算法将初始信号从测量值中解码出来[8]。

重构算法是压缩传感理论的关键和核心内容，它的前提条件是信号在某些变换域或者紧框架下可以进行稀疏表示。重构算法的本质就是寻求信号的最稀疏表示方式，理论证明该过程可以等价转化为l0优化问题。但l0问题又是一个NP-hard问题，有无穷个解，理论证明当测量矩阵满足受限等距特性即RIP准则时，可以将l0等价转化为l1优化问题[5]。l1问题易于求解，又被称为基追踪算法(BP)[9]，然而由于l1算法重构速度较慢，而贪婪算法由于重构速度快的特性，因此被逐渐采用，贪婪算法典型的有匹配追踪系列算法。由于l1算法以及贪婪算法只是通过l1优化问题对重构问题进行间接求解，二者都没有直接求解l0优化问题，Kings-bury等则针对该问题提出了迭代阈值法[10-11]，除上述算法外还被广泛应用的算法有最小全变分法(TV法)以及各种改进算法。

然而目前大多数重构算法主要停留在理论研究和图像的仿真重构上，由于现有的重构算法要求一次性采集整幅图像的数据，因此并不适合于对大规模图像进行实时采集，而且这些算法主要是非线性重构算法，重构代价相对较高。借鉴于分块DCT编码技术在JPEG以及MPEG中的成功应用，Lu Gan实时地提出了分块CS理论[12]，并提出了最小均方差线性估计方法(MMSE)，该理论与现有CS理论相比，更简便、有效，而且能够有效地捕获自然图像中较为复杂的结构信息，而且有着较低的硬件实现成本，具有良好的应用潜力。

文中将详细介绍MMSE算法，并将其与贪婪算法中的匹配追踪(MP)[13]、正交匹配追踪(OMP)[14]以及正则化的正交匹配追踪(ROMP)[15]算法进行仿真对比，上述算法目前具有良好的代表性以及较高的使用频率。通过对比可以体现出MMSE算法的优越性，及其在实践应用中的潜力，并进一步搭建了光学成像系统将压缩传感理论进行了硬件实现，对其实践性进行了探索，实验结果表明该系统有着良好的工作性能，对压缩传感理论的实践应用具有一定的指导作用。

1 分块采样

目前压缩传感理论仍主要停留在理论研究阶段，特别不适合对自然图像进行实时传感，现有的算法需要首先取得目标图像的完整数据，导致重构成本非常昂贵。

文中对自然图像采用分块采样技术[12]，以加快重构速度。自然图像首先被划分为若干个块，每个块采用相同的测量矩阵进行独立地采样，采用分块采样技术的优点主要在于：

(1)测量矩阵的大小极大地降低，便于存储和实现；

(2)由于每次传递的只是部分采样数据而不是整幅图像的数据，因此分块采样具有更加良好的实时性；

(3)由于每个块是独立的，每个块能较容易的得到初始重构解，因此整个重构过程的速度能够得到较大的提高。

2 最小均方差线性估计[15]

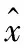
式中Rxx为输入信号的自相关函数，它采用AR的相关系数为0．95的模型来近似。

由于ΦΒ的尺度较小，因此MMSE算法易于实现。

为了进一步提高图像的重构质量，算法利用信号的稀疏性，采用了非线性重构算法进一步对图像质量进行了提高。采用的非线性重构算法主要是硬阈值去噪法和凸集上的交替投影法。

3 仿真结果对比及分析

为了说明上述算法的重构效果，文中采用像素大小为256×256的Lena图像进行仿真重构。算法中采用小波变换作为稀疏变换基，高斯随机矩阵作为测量矩阵，为便于测量矩阵的生成以及加快重构过程，采用分块采样技术将原始Lena图像分成像素大小为64×64的图像块。

文中将MMSE算法与MP、OMP、ROMP算法进行了不同角度的对比，图1为Lena原始图像，图2为Lena图像在采样率10%时，MP、OMP、ROMP以及MMSE算法的重建效果。由图可见在采样率相同的情况下，MMSE算法进行图像重构的效果明显优于MP、OMP和ROMP算法，这三者要采样率为50%时方能达到此重构效果。

图1 Lena原始图像

(a)MP算法

(b)OMP算法

(c)ROMP算法

(d)MMSE算法

为了进一步说明各算法的重构性能，图3显示了在不同采样率下分块处理的MP、OMP、ROMP以及MMSE算法峰值信噪比(psnr)、重构误差以及重构时间曲线对比。

由图4可以看出，MMSE算法在峰值信噪比、重构误差上明显优于经典的MP、OMP、ROMP算法。而且随着采样率的提高，各算法重构质量明显提高，但MMSE算法的重构效果始终明显优于MP、OMP、ROMP算法。当采样率为10%时，后3种算法的重建效果较差，无法重构出原始图像，但MMSE算法在该采样率下仍然表现出较高的重构质量，重构出原始图像，体现出极大的优越性。

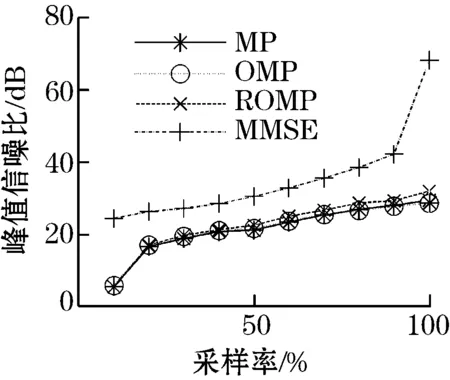
(a)不同采样率下峰值信噪比对比

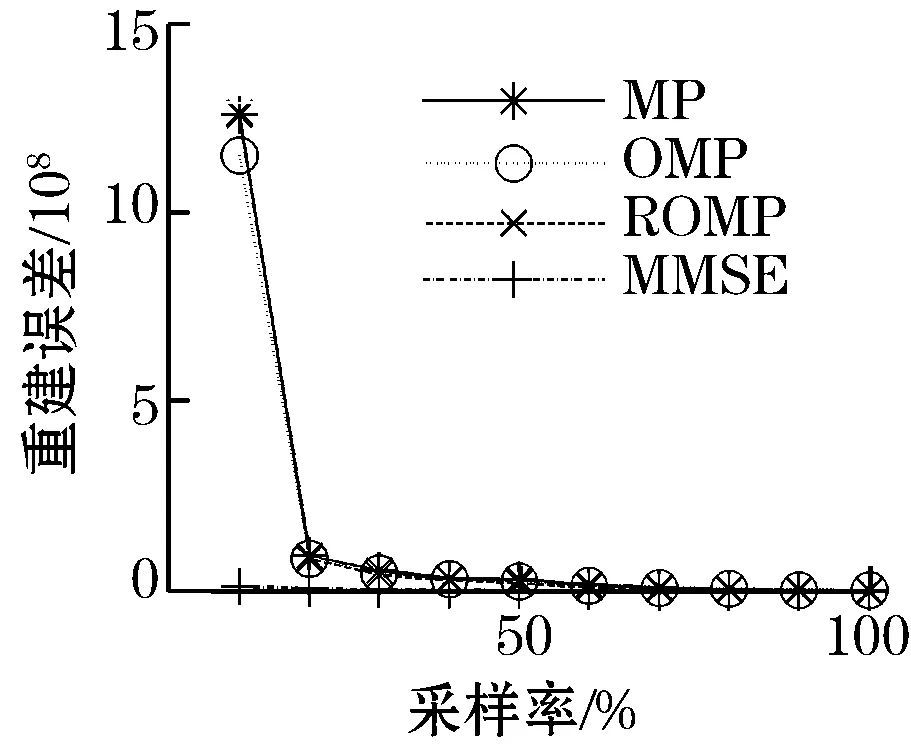
(b)不同采样率下重构误差对比

(c)不同采样率下图像重构时间对比图3 算法性能比较

由仿真结果可知，MMSE算法在低采样率下重构效果优势明显，虽然该算法重构速度稍微较慢，但可通过代码的改进和优化进一步提高代码的执行效率，进而加快算法的重构速度。

目前包括MP、OMP、ROMP算法在内的大部分重构算法主要停留在理论研究阶段，用于图像仿真重构，少有涉及工程图像重构，主要原因在于现有的重构算法都是以矩阵为前提框架，它们更适用于矩阵化处理，而非向量式运算，而在实物重构中，物体图像和重构模型更接近于矢量形式，因此从这个意义上来说，很大程度的限制了MP、OMP、ROMP等算法在工程实践中的应用。而由上文MMSE算法描述可知，MMSE是把图像数据向量化后再进行处理，这与实物重构模型更为接近，也决定了MMSE算法与MP、OMP、ROMP等算法相比，更适用于实物图像重构，具有良好的应用前景，且MMSE算法在低采样率下较高的重构效果更能体现出算法的优越性，较大的节省了存储空间，提高重构质量，体现出压缩传感理论的优点。

4 光学单点成像系统

文中对压缩传感理论的实践应用进行了探究，初步搭建了硬件系统，应用压缩传感理论进行图像重构，系统原理图如图4(a)所示，实物图如图4(b)所示。

系统由LED光源、一对透镜、待测样品以及一系列编码块组成，系统中编码块是通过在透明薄膜上覆盖不同形状的铜膜组成，编码块图案如图5(a)所示，透明的区域允许光线通过，被铜膜覆盖的区域则阻碍光线的通过，以此来实现对光线的调制，待测样品则是一些字符，如图5(b)所示，每个编码块和样品像素都是20×20，大小为32 mm×32 mm×32 mm．

(a)原理图

(b)实物图图4 单点成像系统

LED光源发出的光线，通过透镜变成平行光后依次通过编码块、待测样品，调制后的光线由透镜聚焦到光电传感器上，由于仅用一个传感器进行单点探测(相比于逐行扫描多点探测而言)，因此构成单点成像系统。通过对测量数据的处理即可实现字符重构，文中采用MMSE重构算法，实验中通过40次测量即可实现字符重构，相当于10%的采样率，相比于传统采样极大地节省了存储空间。

(a)编码块

(b)待测样品

系统中对一系列字符进行重构，其仿真与实验结果如图6、图7所示。

图6 字符FZU_NDT仿真重构结果

图7 字符FZU_NDT实验重构结果

由图6、图7可以看出，在该单点成像系统中采用MMSE算法进行字符重构，具有较好的重构效果，虽然在某些区域存在瑕疵，但通过对器件、光路等的调节，可进一步提高重构质量。

该系统是将压缩传感理论进行硬件化实现，对该理论进行初步性的实践探索，旨在为压缩传感理论的实践应用起到初步的启迪和借鉴作用，当然该系统还有较大的改进空间，通过对器件、光路以及算法的优化，能够进一步提高重构质量，改善系统的总体性能。

5 总结和展望

压缩传感理论将传统的信号采样与压缩过程相结合，突破了采样定理的限制，使得宽带信号的采集和处理成为了可能，引发了信号处理领域的革命性变化。

文中介绍了最小均方差线性估计(MMSE)方法，它重构质量好，便于应用于工程实践。文中通过将它与重构算法中使用频率较高且具代表性的MP、OMP、ROMP算法进行仿真对比，突出了MMSE算法的优越性；并对其应用进行探索，通过搭建的单点成像系统将压缩传感理论应用于字符重构。实验结果表明该算法在实践中也有着较好的应用，对于将压缩传感理论应用于实践中有着良好的指导作用。如何构建性能良好、通用的硬件系统，将压缩传感理论应用于实践则仍是一个值得研究的难题，也是未来压缩传感理论的发展方向，在该领域内的突破将引起采样领域的重大变革。

[1] 石光明，刘丹华，高大化，等．压缩感知理论极其研究进展．电子学报，2009，37(5)：1070-1081．

[2] 喻玲娟，谢晓春．压缩感知理论简介．电视技术，2008，32(12)：16-18．

[3] DONOHO D L．Compressed sensing．IEEE Transactions on Information Theory，2006，52(4)：1289-1306．

[4] CANDES E，ROMBERG J，TAO T．Robust uncertainty principles：exact signal reconstruction from highly incomplete frequency information．IEEE Transactions on Information Theory，2006，52(2)：489-509．

[5] CANDES E，ROMBERG J．Quantitative robust uncertainty principles and optimally sparse decompositions．Foundations of Comput Math，2006，6(2)：227-254．

[6] CANDES E．Compressive sampling．Proceedings of International Congress of Mathematicians．Madrid，2006，3：1433-1452．

[7] CANDES E，ROMBERG J．Practical signal recovery from randomprojections[EB/OL]．http：//www．Acm．Caltech．edu/～emmanuel/papers/PracticalRecovery．pdf．

[8] 金坚，谷源涛，梅顺良．压缩采样技术及其应用．电子与信息学报，2010，32(2)：470-474．

[9] CHEN S S，DONOHO D L，SAUNDERS M A．Atomic Decomposition by Basis Pursuit．SIAM J．Sci．Comput，1998，20(1)：33-61．

[10] KINGSBURY N．Complex wavelets for shift invariant analysisand filtering of complex wavelets for shift invariant analysisand filtering of signals．Applied and Computational Harmonic Analysis，2001，10(3)：234-253．

[11] HERRITY K K，GILBERT A C，TROPP J A．Sparse approximation via iterative thresholding．In：Proceedings of the IEEE International Conference on Acoustics，Speech and Signal Processing，Washington D．C．IEEE，2006：624-627．

[12] GAN L．Block compressed sensing of natural images．In：Proceeding of the 15th International Conference on Digital Signal Processing．Washington D．C．，USA：IEEE，2007．403-406．

[13] MALLAT S，ZHANG Z．Matching pursuit in a time-frequency dictionary．IEEE Trans Signal Processing，1993，41(12)：3397-3415．

[14] TROPP J A，GILBERT A C．Signal recovery from random measurements via orthogonal matching pursuit．IEEE Transactions on Information Theory，2007，53(12)：4655-4666．

[15] NEEDELL D，VERSHYNIN R．Greedy signal recovery and uncertainty principles．In：Proceedings of the Conference on Computational Imaging．San Jose，2008：1-12．

Single-point Imaging System Based on Compressive Sensing Technique

ZHANG Tao1， ZHONG Shun-cong1，2，Shen Yao-chun3，YAO Li-gang1

(1．Laboratory of Non-destructive Testing & Evaluation，School of Mechanical Engineering and Automation，Fuzhou University，Fuzhou 350108，China；2．Key Laboratory of Safety Science of Pressurized System of Ministry of Education，East China University of Science and Technology，Shanghai 200237，China；3．Fujian Provincial R&D Centre for Medical Equipment，Fuzhou 350000，China;4．School of Electrical Engineering and Electronics，University of Liverpool，UK)

Compressed Sensing (CS) represented compressible signals at a sampling rate significantly below the Nyquist frequency. Global observations of the sparse signal can be taken and the original signal can be accurately reconstructed from few observations. It broke through the bottleneck of Shannon sampling theorem and made it possible to deal with broadband and high resolution signals. The compressed sensing mostly stayed in the theoretical research and simulation phase, rarely involved the theory of hardware for practical application. The minimum mean square error linear estimate (MMSE) algorithm was introduced in this paper. Compared with the commonly used reconstruction algorithms, MMSE showed better reconstruction quality under low sampling rates and had great potential in real applications. Furthermore, a single-point imaging system was conducted to use CS in practice. It demonstrates the system works well and has great values in applications.

compressive sensing;sparsity;reconstruction algorithms;MMSE;imaging system

国家自然科学基金资助项目(51005077);福建省杰出青年基金资助项目(2011J06020);教育部高学校博士学科点科研基金资助项目(博导类，20133514110008);国家卫生和计划生育委员会科研基金项目(WKJ-FJ-27)；厦门特种设备检验院资助项目。

2014-01-10 收修改稿日期：2014-11-10

TP23

A

1002-1841(2015)01-0088-04

张涛(1989—)，硕士研究生，主要从事无损检测及仪器方面的研究。E-mail：fdmxh@sina．com