基于智能数字锁相技术的光栅细分方法

郭雨梅，苏 升

(沈阳工业大学信息科学与工程学院，辽宁沈阳 110870)



基于智能数字锁相技术的光栅细分方法

郭雨梅，苏 升

(沈阳工业大学信息科学与工程学院，辽宁沈阳 110870)

在高精度数字集成化光栅测控系统的研制过程中，光栅传感器输出信号的细分方法至关重要。为了在保证跟踪速度的前提下提高光栅传感器的细分精度，提出了基于智能数字锁相技术的光栅细分方法。研究了该方法中光栅跟踪速度与细分数的关系，所设计的智能K模计数器可根据不同的捕获过程来选择合适的K值，从而在保证输出信号稳定的情况下，缩短锁相时间，提高跟踪速度。利用FPGA设计并实现了该方法，通过仿真验证了其正确性，为数字集成化光栅测控系统的研制奠定了基础。

锁相倍频；光栅传感器；FPGA；信号处理

0 引言

光栅传感器的细分精度是精密机械加工行业的保障，如何在保证跟踪速度的前提下提高光栅传感器的细分精度，对我国装备制造业、国防建设以及科学技术的发展具有重要的现实意义。

常用的光栅传感器细分方法有直接细分法、移相电阻链法、幅度分割法以及载波调制法等。直接细分法虽然电路结构较为简单，但是无法满足高精度细分的要求；移相电阻链法通过电阻元件实现细分，随着细分数的提高，电路的复杂度也提高，同时电阻元件具有一定的温漂，精度难以保证；幅度分割法可以获得较高的细分数，但是电路较为复杂；载波调制法的精度较高，但是电路对信号的正交性要求较为严格，同时电路的复杂度也较高[1]。

文中提出的基于智能数字锁相技术的光栅细分方法，在保证光栅传感器跟踪速度的前提下使光栅传感器的细分数最大化。通过FPGA实现智能数字锁相倍频算法，利用智能锁相倍频技术，提高了光栅传感器的细分精度，缩短了锁相时间，为精密机械加工的实现奠定了基础。

1 锁相倍频细分中光栅跟踪速度与细分数的关系

在数字锁相环系统中，鉴相器通常为异或门鉴相器，异或门鉴相器的增益大小是2/π的函数；数控振荡器的输出频率为输入频率的N倍，即如果光栅传感器的输出频率为f0，则数控振荡器的输出频率为Nf0；环路滤波器实质是一个数控的滤波器，其主要通过加脉冲和减脉冲计数器实现，加减脉冲计数器的模值大小通常设为K，加减脉冲计数器的时钟频率为信号输入频率的M倍。根据以上描述，可以将环路滤波器的传递函数表示为

截止频率的大小为

在实际应用中，光栅传感器具有一定范围的跟踪速度，设其跟踪速度的大小为v，并且光栅尺的栅距大小为d，则输出频率为

则跟踪速度的截止频率为

在上式中，v-3db即为光栅传感器的跟踪速度，该跟踪速度的大小与M、f0、d成正比，通常情况下，光栅传感器的栅距d为固定值，以50线/mm的光栅传感器为例，其栅距大小为0．02 mm．M与f0的值越大，跟踪速度越大[2]。同时，K和N的值越小，跟踪速度越大。在数字锁相环系统中，K值的选取尤为重要，K值太小，虽然锁相时间较短，但是K模计数器会向加减脉冲计数器单元频繁地输出借位或者进位脉冲，使得输出频率的相位产生抖动，进而致使锁相环处于稳定状态时，输出误差较大。如果K值较大，则锁相环系统进入锁相的时间较长，但是输出噪声将会减小。为了保证锁相时间，同时使得输出信号较为稳定，该系统设计了智能K模计数器，可根据不同的捕获过程选择合适的K值。

实际应用时，f0为1．5 MHz，M为64，N为200，K值由智能控制模块实时获得。

2 智能数字锁相环的设计

锁相环技术近年来日趋完善，并且不断地应用于倍频、信号处理、高速时钟等场合，该技术在通信系统以及测控系统中得到良好的应用。传统的模拟锁相环是通过集成电路进行设计，构成组成锁相环的相应模块，完成锁相倍频的功能。但是传统锁相环由于集成度不高，因此频率上限较低，同时稳定性较差。与传统的模拟锁相环相比，数字锁相环具有较高的稳定性和灵活性，可以通过数字的方法得到可调的输出频率，具有较高的实用价值[3]。

文中利用FPGA设计数字锁相环，并将该数字锁相环应用于光栅细分系统中，在保证光栅跟踪速度的前提下得到了较高的分辨率。

2．1 数字锁相环的工作原理

由锁相环的工作特性可知，数字锁相环是由数字鉴相器、环路滤波器、数控振荡器以及N分频器构成。为了保证锁相环的同步时间，提高输出信号的稳定性，系统设计了智能控制模块，从而实时调整K值的大小[4]。数字锁相环的原理框图如图1所示。

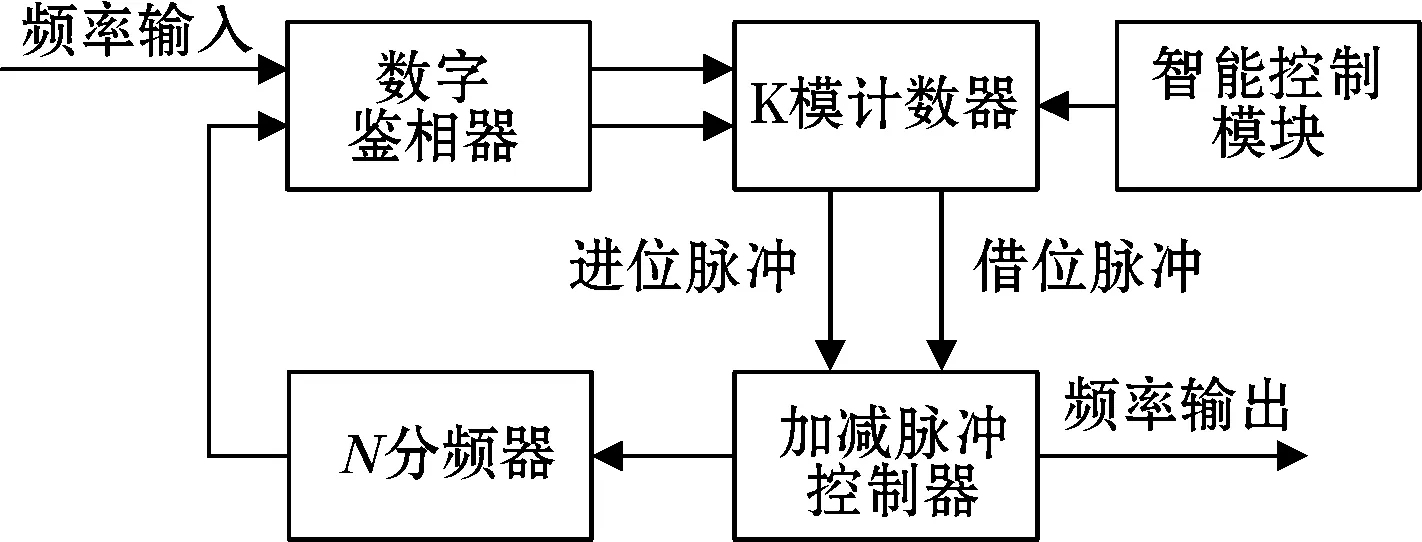
图1 数字锁相环的原理框图

从数字锁相环的原理框图可以看出，数字鉴相器有两路输入，其中一路是原始的频率输入信号，另外一路为数字锁相环的反馈信号。该两路信号具有相同的频率特性，但是却具有一定的相位差，根据两路信号相位差的大小，可以控制K模计数器进行计数。K模计数器的主要参数为计数值的大小，根据数字鉴相器的鉴相结果，K模计数器对参考时钟进行计数，同时输出进位脉冲或者借位脉冲，进位脉冲和借位脉冲的作用是使加减脉冲控制器的输出频率产生变化，从而使得输出频率逐渐逼近设定值。N分频器的作用是对输出频率进行分频，从而使得反馈信号的频率与输入信号的频率保持一致，使数字锁相环构成一个闭环系统。

2．2 数字鉴相器的实现

鉴相器在工作时对两路输入信号进行异或操作，异或的结果是占空比为50%的方波时，表示相位进入锁定状态，此时输出频率稳定。异或结果是非占空比为50%的方波时，表示锁相环系统处于捕捉状态，此时输出频率不稳定[5]。所设计的数字鉴相器的仿真结果分别如图2和图3所示，其中图2为相位进入锁定状态的仿真结果，图3为相位未进入锁定状态的仿真结果。signal_in和signal_out是鉴相器的两路输入信号，且signal_in是系统的输入时钟信号，signal_out是反馈的时钟信号，即经过N分频器后的分频信号，dpout为鉴相器的输出信号。通过仿真波形可以看出，当signal_in和signal_out相位相差90°时，鉴相器的输出为50%的方波信号，此时锁相环进入锁定状态。

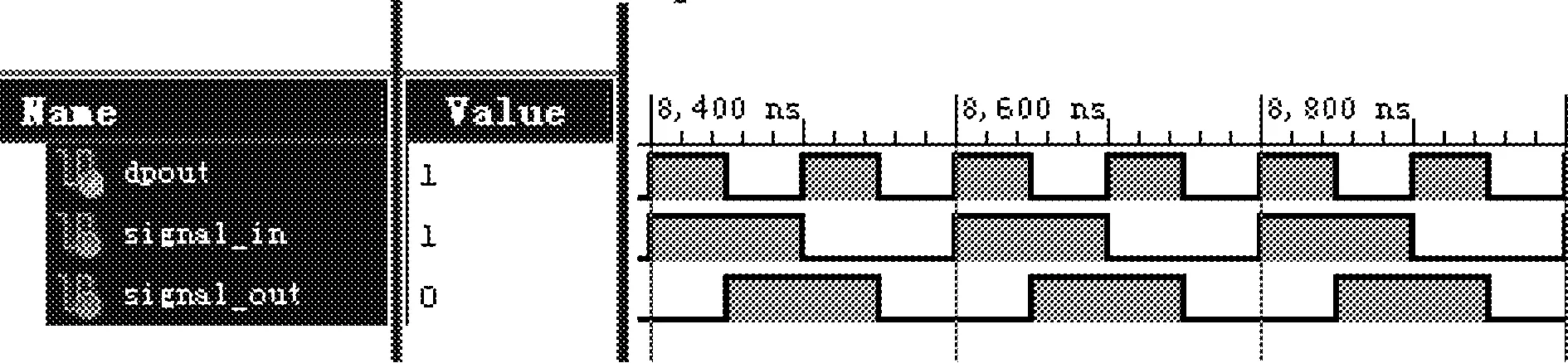
图2 进入锁定状态的仿真结果

图3 未进入锁定状态的仿真结果

2．3 智能控制模块的设计

系统所设计的智能K模计数器可自动检测输入频率与输出频率的相位差，从而选定K值。智能K模计数器由3部分组成，分别为检测部分、比较部分和模数控制部分。检测部分的主要作用是检测输入信号与输出信号的相位差，检测部分将实时输出相位差序列，该相位差序列通过比较部分使得模数控制部分选定合适的K值。根据K值的大小，锁相的过程分为3个时间区，分别为快速捕获区、慢速捕获区以及同步时间区。

检测部分的实际电路如图4所示，2个D触发器的D端均接至为逻辑1，此时2个D触发器的输出端Q值将受控于输入端CLK的状态，根据原理图可知，D1触发器的CLK为fin，而D2触发器的CLK为fout.如果fin的相位超前于fout，则Q1的输出先置高。当2个D触发器的输出均为高电平后，与非门的状态为低电平，同时，2个D触发器的状态将被自动清除，在复位时，输出信号会有毛刺出现，该毛刺的时间宽度受触发器的延时影响。而该设计直接通过FPGA内部的逻辑门构成逻辑电路，使得毛刺的影响降为最低。检测电路的输出将送至比较部分，从而确定实时的K值大小。

图4 智能控制模块检测部分原理图

2．4 K模计数器的设计

在模拟锁相环系统中，鉴相器的输出需要经过环路滤波器进行滤波，从而产生控制压控振荡器的直流电平，而在数字锁相环中，需要设计数字环路滤波器，从而控制数控振荡器产生特定频率的信号[6]。常用的数字环路滤波器有高低电平计数器和K模计数器。该设计中，通过FPGA实现K模计数器，完成锁相环的数字环路滤波器的设计。

K模计数器内部包括两个独立的计数器，该两个独立的计数器均为加计数器，加计数器的计数范围为0～K-1，常用的K值为2的整数倍。当异或门鉴相器的输出结果为低电平时，计数器1开始工作，并且当计数值为K-1时，输出一个加脉冲。当异或门鉴相器的输出结果为高电平时，计数器2开始工作，并且当计数值为K-1时，输出一个减脉冲。K模计数器输出加脉冲和减脉冲可以作为加减脉冲控制电器的输入信号，从而调节锁相环的输出频率。

在FPGA中通过Verilog程序对K模计数器进行设计，K模计数器的仿真波形分别如图5和图6所示。其中，图5为鉴相器输出即dpout为低电平时，K模计数器的输出仿真波形，图6为鉴相器输出为高电平时，K模计数器的输出仿真波形。由仿真波形可以看出，当异或结果dpout为低电平时，每计数满K即4个clk，addclk_out会输出一个脉冲，使得加脉冲信号有一个周期的输出，而delclk_out一直保持低电平；当异或结果为高电平时，每计数满K即4个clk，delclk_out会输出一个脉冲，使得减脉冲信号有一个周期的输出，而addclk_out一直保持低电平。

图5 鉴相器输出为低电平时K模计数器的输出仿真波形

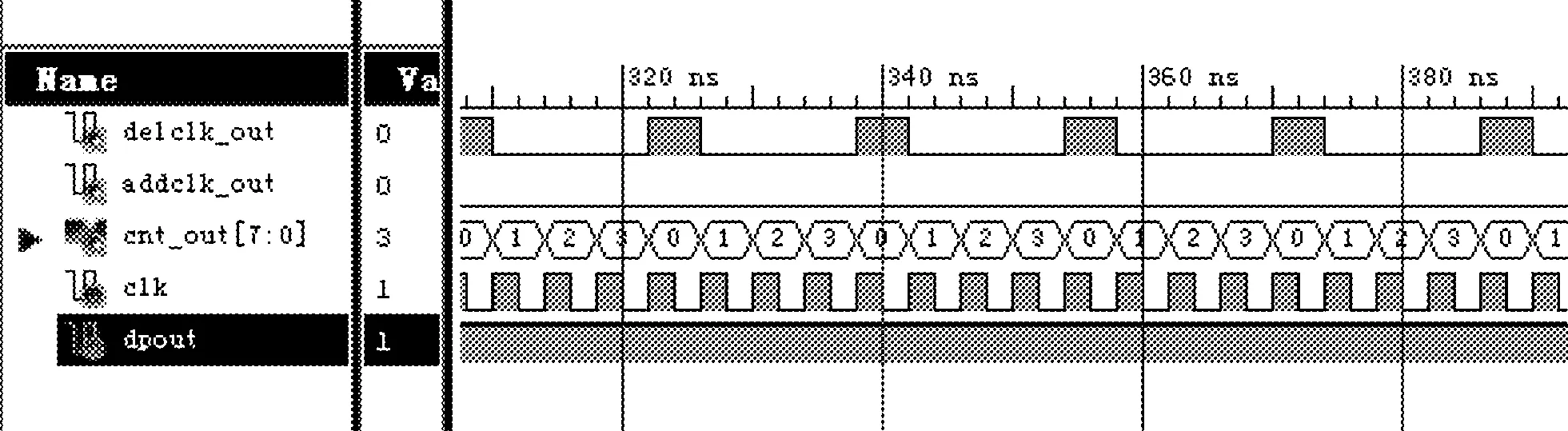
图6 鉴相器输出为高电平时K模计数器的输出仿真波形

2．5 加减脉冲控制器的设计

加减脉冲控制器实质是数控振荡器，其主要作用是根据K模计数器的结果对输出频率进行调节，从而使得输出频率达到锁定的状态，完成锁相倍频的作用。加减脉冲控制器的主要工作过程为，当K模计数器输出一个加脉冲信号时，加减脉冲控制器控制输出频率增加，当K模计数器输出一个减脉冲信号时，加减脉冲控制器控制输出频率减少，从而使得输出频率达到平衡状态[7]。

如图7所示，当有addclk信号，即加脉冲信号到来后，计数的暂存值增加1，而当有delclk信号，即减脉冲信号到来后，计数的暂存值将减1，完成脉冲加减功能，从而对输出频率进行合理调节。

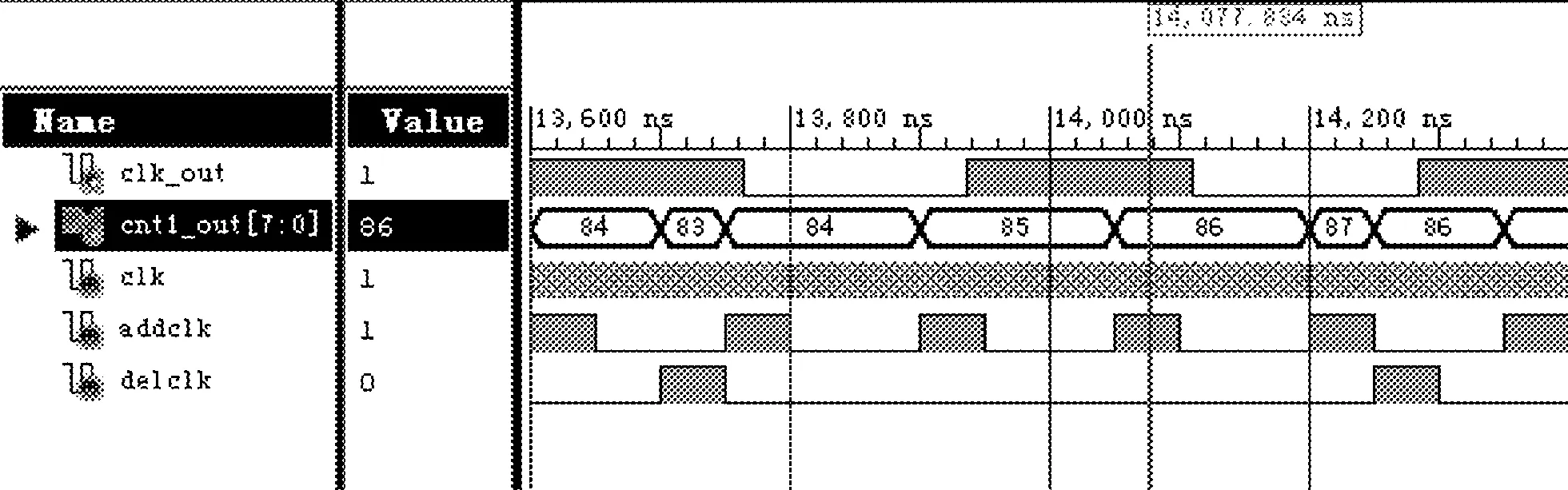
图7 加减脉冲控制器的仿真波形

图8为加减脉冲控制器的局部仿真波形图，clk的周期为2 ns，由波形图可知，当cnt1_out的值为255时，通过时间测量功能可以得出，clk_out的高电平时间为512 ns，即clk的255个周期，从而验证Verilog编程的正确性。在clk_out为高电平期间，不断有addclk信号和delclk信号输入，如果有addclk信号输入，则cnt1_out的值会增加，如果有delclk信号输入，则cnt1_out的值会减少。由于clk_out的值为255后会保持稳定，故此时若仍有addclk输入，clk_out的值将保持不变。在图8中，仿真时间为0～512 ns区间内时，cnt1_out的值保持255，但中间有变化，该变化即为delclk引起，而在delclk信号之后，又有addclk脉冲，故cnt1_out又稳定在255.

2．6N分频器的设计

N分频器的主要作用是对锁相倍频之后的信号进行分频操作，从而将分频后的波形反馈给数字鉴相器，使得整个锁相环系统处于闭环状态[8]。

系统硬件设计时，选用了50线/mm的光栅传感器作为前端输入传感器，而50线/mm光栅传感器的分辨率仅为0．02 mm，若要达到分辨率为0．1 μm的实际精度，需要对光栅信号进行200细分，故实际设计N分频器时，需根据要求的分辨率选用不同的分频系数。

在FPGA中，主要通过计数器的方式设计N分频器，软件设计过程中，对输出频率进行计数操作，计数值可以通过软件进行计算，从而使得倍频的频率可以设定。在实际应用过程中，不断地对分频器的分频系数进行调节，从而使得光栅的实际精度达到要求。

3 结束语

光栅传感器细分方法的决定着光栅测控系统的测量精度。文中基于锁相倍频方法，研究了光栅传感器跟踪速度与细分数之间的关系，提出了基于智能数字锁相技术的光栅细分方法，所设计的智能K模计数器可自动检测输入频率与输出频率的相位差，从而选定K值。在保证锁相时间的同时使输出频率更为稳定，达到更好的跟踪效果。利用FPGA通过Verilog程序设计并实现了该方法，通过仿真验证了方法的合理性与正确性，为光栅传感器的数字锁相倍频细分提供了一种新思路。

[1] 刘世峰．基于幅值采样的光栅莫尔条纹信号细分技术的研究：[学位论文]．武汉：华中科技大学，2007．

[2] 孟凡波．基于FPGA的光栅数显装置的研究与设计：[学位论文]．沈阳：沈阳工业大学，2011．

[3] 叶盛祥．光电位移精密测量技术．成都：四川科学技术出版社，2003．

[4] 庞辉．智能模数控制型全数字锁相环的研究：[学位论文]．合肥：安徽大学，2012．

[5] 吴剑峰，沙杰，汪敏．M224型半自动内圆磨床数控化改造技术．控制与检测，2010(5)：56-59．

[6] 张兴全．机床的光栅测量和数控系统的发展趋势．数字化制造技术与装备最新发展国际论坛文集，武汉，2005．

[7] 马骁．光栅振动检测系统中信号处理关键技术的研究：[学位论文]．天津：天津大学，2009．

[8] 苏绍璟．大量程纳米级光栅位移测量理论及关键技术研究：[学位论文]．长沙：国防科技大学，2001．

Grating Segmentation Method Based onIntelligent Digital Phase Locking Technique

GUO Yu-mei，Su Sheng

(School of Information Science and Engineering，Shenyang University of Technology，Shenyang 110870，China)

The subdivision method of output signal of the grating sensor is very important in the development process of digital integrated grating measurement and control system with high precision. In order to improve the segmentation accuracy of grating sensor in the premise of ensuring the tracking speed, the grating segmentation method based on intelligent digital phase locking technique was put forward and the relationship between the fine fraction and grating tracking speed was studied. The designed intelligent K counter can choose suitable K values according to different capture processes, thus shortening the lock time and improving the tracking speed in the case of stable output signal. The algorithm was designed and implemented by FPGA and the correctness of the algorithm was verified by simulation, thus laying the foundation for the development of digital integrated grating measurement and control system.

phase-locked frequency multiplication; grating sensor; FPGA; signal processing

沈阳市科技计划资助项目(F13-316-1-57)

2014-01-14 收修改稿日期：2014-11-09

TH711

A

1002-1841(2015)01-0104-04

郭雨梅(1965—)，教授，博士，主要从事现代检测技术及装置、智能仪器和网络化测控技术等方面的研究。 E-mail：gym112@163．com