基于Copula函数的韩江流域干支流洪水遭遇分析*

关 帅，林颖妍，查悉妮，丁 波，陶 楠，2，刘祖发

(1.中山大学水资源与环境研究中心//华南地区水循环与水安全广东省普通高校重点实验室，广东广州510275;2.广东省水利厅农村机电局，广东广州510635)

研究洪水的遭遇问题，对流域内防洪减灾和洪水规律的认识有着重要的意义。根据研究区域历年同步洪水资料进行统计仍是目前经常使用的方法，但这只能对已发生洪水进行简单的分析计算［1－2］，无法定量估算百年一遇或千年一遇等设计洪水的遭遇风险。洪水遭遇是一个多变量的频率组合事件，因此可以采用多变量的分析方法对其进行研究。目前，多变量水文分析方法主要有经验频率法、非参数法、特定边缘分布构成的联合分布法、多元正态分布法、将多维转换成一维的方法等，但各法均存在各自的局限和不足［3－5］，无法准确描述水文事件的内在规律。Copula函数克服了这些方法的不足，它通过任意边缘分布和相关性结构来构造多维联合概率分布，具有很大的灵活性和适应性［6－8］。近年来，Copula 函数广泛应用于暴雨［9－10］、洪水［11－12］和干旱的多特征属性频率分析［13－14］、雨洪遭遇［15］以及洪水遭遇［16］等问题。

韩江流域是广东省的第二大流域，韩江下游是人口稠密经济发达的潮汕平原。流域内水系主要由梅江、汀江和韩江三大水系组成，其中梅江是韩江的主流上游，汀江是韩江的一级支流，韩江的主要洪水就来自梅江和汀江，若两江相遇或梅江、汀江连续洪水叠加，都会造成韩江下游发生大洪水。根据历史文献记载统计，韩江平均每8年就发一次大水，对流域内人民的生命和财产安全造成了极大的威胁。目前对于韩江流域洪水的研究，主要集中在单次的暴雨洪水分析［17］、暴雨洪水的移植计算［18］以及年径流演变过程［19］等方面，而对于韩江流域内三大水系联合分布，尤其是干流 (上游)和支流(下游)洪水量级之间的相互作用尚无人研究过。本文利用二维和三维Copula函数，构建梅江、汀江和韩江之间的联合分布，分析韩江流域干支流洪水遭遇的规律和特征，以期为韩江流域洪水规律的认识和防洪减灾提供理论参考和决策支持。

1 研究区域概况及数据来源

1.1 研究区域概况

韩江流域是广东境内仅次于珠江的第二大流域，在广东的经济社会发展中占有十分重要的地位。流域范围包括广东、福建、江西3省共22个县市，流域面积约3万km2;北面接江西省赣江流域，东面接闽江黄岗河流域，南面接榕江流域，西面接东江流域，地理位置相当优越。韩江发源于广东省紫金县的七星岽，上游称琴江，流至五华水寨后称梅江，由西南向东北至大埔县的三河坝与由福建省流来的汀江汇合后称韩江，见图1。在潮州市分为东、西、北溪经汕头市的五大出海口流入南海，干流长470 km。

图1 研究区域和水文站位置Fig.1 Research area and hydrological station locations

韩江流域属亚热带气候，水量丰富，多年平均降雨量高达1620 mm。由于流域内以热带气旋雨影响为主，暴雨大且集中，所以洪水峰高量大，且多发生在6月和8月。通过对实测资料及历史洪水分析，韩江流域洪水具有较明显的时空性，干支流具有各自不同特点的洪水过程，从总体上看，梅江洪水量大，洪水过程线较肥胖，汀江峰高呈尖瘦型［18］。

1.2 数据来源

本文收集了1954－2003年梅江横山站的实测逐日平均流量资料，1959－2010年汀江溪口站的实测逐日平均流量资料，1947－2011年韩江潮安站的实测逐日平均流量资料。由于位于汀江上游的棉花滩水库于2001年竣工，为了避免棉花滩水库影响选取资料的一致性，同时保持三站数据资料的同步，本文选取1959－2000年逐日平均流量，采用年最大值取样法进行独立取样，得到1959－2000年横山、溪口和潮安站最大日平均流量。

2 研究方法

2.1 Copula函数

Copula［20］函数是定义域为 ［0，1］均匀分布的多维联合分布函数，它将联合分布分为变量的边缘分布和变量间的相关性结构分别处理，而且不要求变量同分布，所以可将多个任意形式的边缘分布连接起来，生成一个多变量联合概率分布模型。Copula函数有多种类型，在水文及相关领域常见的也是本文用来构造梅江、汀江和韩江站两两间联合分布的4种二维Archimedean Copula函数分别是:Gumbel-Hougaard(GH)Copula、 FrankCopula、Clayton Copula和 Ali-Mikhail-Haq(AMH)Copula。三维Archimedean Copula函数可以由二维Archimedean Copula函数通过一重嵌套得到，本文选择三维Gumbel-Hougaard(GH)Copula来构造梅江、汀江和韩江3者之间的联合分布，它又分为对称型和不对称型两种。

2.2 边缘分布的确定与检验

确定不同变量的边缘分布函数是构建Copula函数的第一步。我国常采用Pearson-III分布作为水文变量的分布线型，但是为了计算的准确性，本文选取国内外应用较为广泛的四种概率分布函数，分别为Pearson-III分布 (P-III)，指数分布 (EXP)，广义极值分布 (GEV)和对数正态分布 (LOGN)，并利用比较稳健的线性距法［21］进行参数估计。采用 Kolmogorov-Smirnov(K-S)［22］方法检验样本理论分布与经验分布的拟合程度，并用概率点据相关系数法 (PPCC)［23］、均方根误差 (RMSE)准则和AIC最小准则法［24］评价确定出与各站数据拟合效果最好的边缘分布。利用以下公式计算边缘分布的经验频率。

式中，P为X≤xi的经验频率;i为样本从小到大排列后的序号;n为样本容量

2.3 参数估计与拟合优度检验

对于二维Copula函数的参数，本文选择用相关性指标法来计算，该方法是根据两变量间的Kendall相关系数与二维Copula函数的参数θ之间的关系来计算θ;对于三维及以上Copula函数，相关性指标法已不再适用，一般用极大似然法估计参数。其中Kendall相关系数的计算公式为:

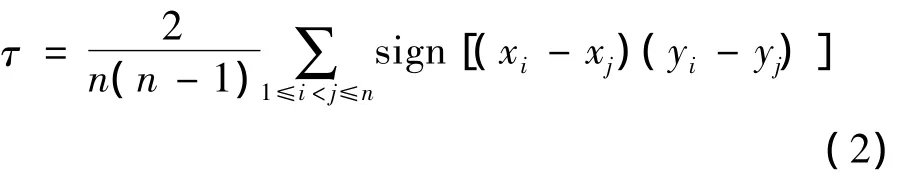
式中，{(x1，y1)，(x2，y2)，…(xn，yn)}为随机样本;sign为符号函数。

然后采用AIC最小准则法和离差平方和最小(OLS)准则评价确定出最优的Copula函数。

2.4 联合重现期和同现重现期

在实际工程应用中，常引入“重现期”概念。所谓重现期是指随机变量的取值在长时期内平均多少年出现一次，又称多少年一遇。重现期T与累计频率P(水文统计上一般采用超值累计频率)有一定的对应关系，对于暴雨洪水事件，T=1/P。对于多变量来说，有联合重现期和同现重现期两种定义:联合重现期是指多个变量中至少有一个超过某一特定值时，事件发生的重现期;同现重现期是指多个变量同时都超过特定值时，事件发生的重现期。

根据定义，两变量X、Y的联合重现期To(x，y)计算公式为:

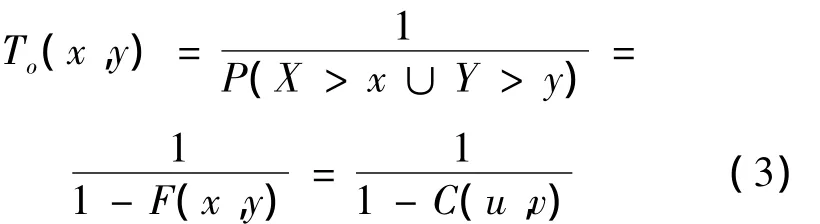
两变量X、Y的同现重现期Ta(x，y)计算公式为:

式中，u、v为边缘分布函数，C(u，v)为联合分布函数。

2.5 条件概率分布及重现期

当采用多个变量来描述水文事件时，得到多变量联合概率分布后，给定某一变量的范围，另一变量在某一区间发生的概率大小问题就是条件概率的问题。比如用潮安站、横山站和溪口站的流量作为特征变量，来描述韩江流域上下游地区的洪水组成，我们想知道当干流韩江潮安站发生大于某一重现期的洪水时，梅江横山站和汀江溪口站发生某一量级的洪水的条件概率多大;或者当梅江横山站和汀江溪口站发生大于某一重现期的洪水时，干流韩江潮安站发生某一量级的洪水的条件概率是多大。

用两变量X、Y来描述一事件时，当X＞x时，Y＞y的条件概率为:

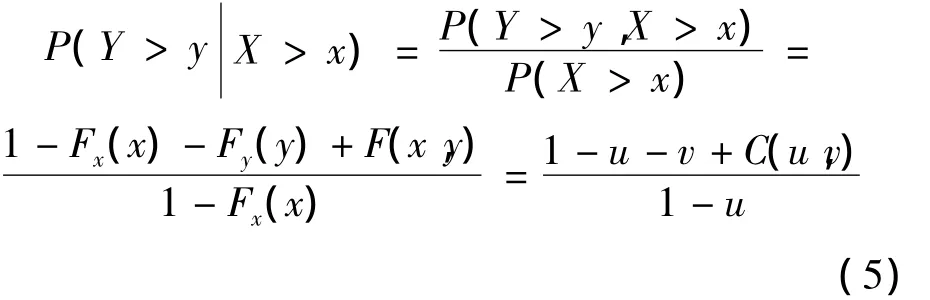
相应的条件重现期为:

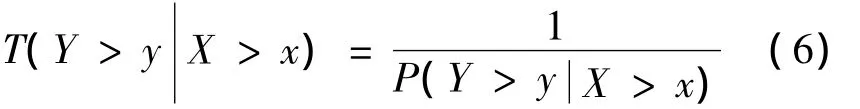
用三变量X、Y、Z来描述一事件时，当X＞x时，Y＞y和Z＞z的条件概率:

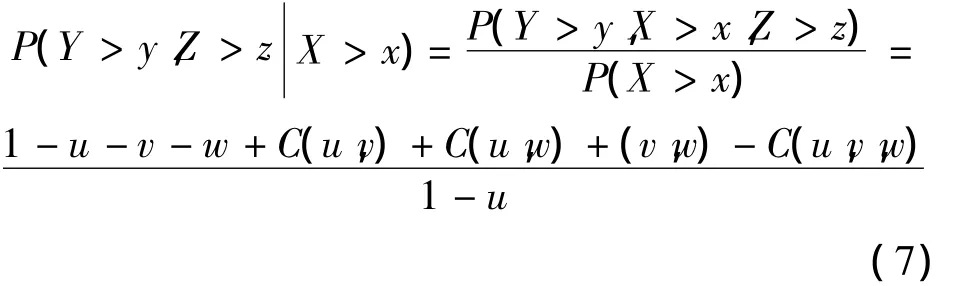
相应的条件重现期为:

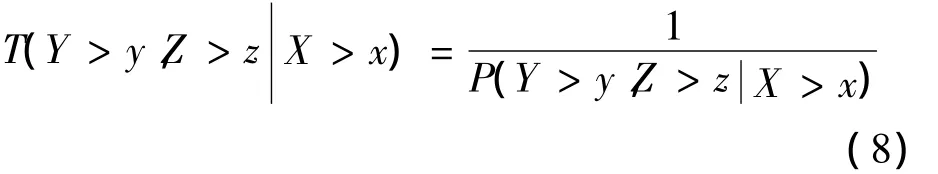
同理可以定义当Y＞y时，X＞x和Z＞z的条件概率及重现期，当Z＞z时，Y＞y和X＞x的条件概率及重现期。

3 结果与讨论

3.1 最大日平均流量边缘分布的确定

Copula函数不限定变量的边缘分布，所以本文选取P-III，EXP，GEV和LOGN等4种应用较为广泛的概率分布函数对梅江、汀江和韩江的最大日平均流量进行拟合，并进行检验与优选，确定出拟合效果最优的边缘分布，拟合度检验结果见表1。其中4种分布的K-S检验值均小于临界值0.2098，即都通过了K-S检验。最终选择PPCC值最大、均方根误差 (RMSE)最小并且AIC值最小的分布作为最优的边缘分布，在表1中用加粗表示。从表1可以看出，潮安站和横山站服从P-III型分布，溪口站服从指数分布。

表1 韩江流域三大水文站边缘分布拟合检验结果1)Table 1 The fittest results of the marginal distributions of the three stations

3.2 最大日平均流量联合分布模型的确定

对于二维Copula函数构造的3大水文站两两间的联合分布，首先根据公式 (2)估算样本的Kendall相关系数τ，然后再根据τ计算3大水文站最大日平均流量二维Copula联合分布的参数，见表2。从中可以看出，潮安站与横山站的Kendall相关系数较大，表明两者关系密切，相关性较好。然后采用AIC最小准则和离差平方和最小准则(OLS)确定拟合效果最好的Copula函数。结果发现，三大水文站两两间最优Copula函数均为GH Copula。

表2 韩江流域三大水文站二维及三维联合分布参数估计结果Table 2 Parameter estimations of 2-dimensional and 3-dimensional joint distributions of the three stations

本文采用三维Gumbel-Hougaard(GH)Copula构造3大水文站的联合分布，首先利用极大似然法进行参数估计，然后同样采用AIC最小准则和OLS最小准则从对称型和非对称型两种函数优选出拟合效果最好的Copula函数。从表2可以看出最优的为三维对称型GH Copula。

3.3 联合概率分布及重现期

图2 韩江流域三大水文站联合概率分布Fig.2 The joint distribution of the three stations

图3 韩江流域三水文站两两间联合重现期等值线图 (a、b、c)和同现重现期等值线图 (d、e、f)Fig.3 The joint return period(a，b，c)and current return period(d，e，f)of Hanjiang Basin

根据三大水文站最大日平均流量两两间的Copula函数，可以得到相应的二维联合分布，并据此计算特定条件下的联合概率，见图2(省略了横山站和溪口站的联合分布图)。根据公式 (3)和(4)，计算其联合重现期和同现重现期，并绘制其等值线图，见图3。根据图2和图3，可以得到三站之间任何一个两两组合的联合分布值、联合重现期和同现重现期。如以1960年6月的大洪水为例，潮安于11日出现年最大流量，横山和溪口站于10日出现年最大流量，三站最大日洪峰流量分别为13300，6810，3900 m3/s，其边缘分布重现期为53.2、50.0、5.6年，该场洪水主要是由梅江地区6001号台风带来的暴雨引起的。潮安和横山站的联合分布函数值为0.9754，联合重现期为40.7年，同现重现期为70.4 a，意味着韩江和梅江其中之一发生超过1960年最大洪水的重现期为40.7 a，两站均发生超过1960年最大洪水的重现期为70.4 a;同理可求得潮安和溪口站联合分布函数值为0.8201，联合重现期为5.6 a，同现重现期为60.6 a;横山和溪口站的联合分布函数值为0.8162，联合重现期为5.4 a，同现重现期为72.5 a;潮安、横山和溪口三站的联合分布函数值为0.8205，联合重现期为5.6 a，同现重现期为131 a。由以上分析可知，潮安和溪口站，横山和溪口站，以及潮安、横山和溪口三站的联合重现期比较小，且都和溪口站的单变量的重现期相差不多，说明这场洪水中汀江并未发生大洪水，主要洪水是由梅江引起的，这与实际情况相吻合。

3.4 三江洪水遭遇分析

韩江、梅江与汀江两两之间以及三江之间的遭遇组合概率可定义为两江 (三江)同时发生大于某一重现期的洪水，即P(Q1＞qT1，Q2＞qT2)、P(Q1＞qT1，Q2＞qT2，Q3＞ qT3)，其中 Q1、Q2、Q3分别代表洪水发生的量级，qT1、qT2、qT3分别代表T年一遇的设计值洪水。表4列出了潮安、横山与溪口重现期分别为1000、200、100、50、20、10 a情况下的设计洪水值和两两之间的遭遇概率。潮安与横山、潮安与溪口、横山与溪口遭遇千年一遇洪水的概率分别为0.0731%、0.0465%、0.0284%，遭遇10年一遇的概率分别为7.4843%、5.0595、3.4574%，低重现期的洪水遭遇比高重现期的洪水遭遇概率大;相同重现期洪水遭遇组合，潮安与横山遭遇的概率大于潮安与溪口，潮安与溪口遭遇的概率大于横山与溪口。

表3 韩江流域三大水文站两两之间洪水发生量级组合遭遇概率Table 3 Coincidence risk analysis of flood magnitudes of two stations %

表4列出了潮安、横山和溪口重现期分别为1000、200、100、50、20、10年情况下三站之间遭遇概率。潮安、横山和溪口同时出现1000、200、100、50、20、10年一遇洪水的遭遇概率分别为0.0243%、0.1226%、0.2479%、0.5063%、1.3453%、2.9610%，比两站同时发生相应重现期的洪水概率要小。对比分析表3和表4可以发现，潮安、横山和溪口同时发生1000、200、100、50、20、10年一遇洪水的遭遇概率与横山和溪口同时发生相应重现期洪水的概率很接近，即当梅江与汀江同时发生洪水时，韩江潮安站出现大洪水几乎是必然事件，这与刘树锋［18］等基于韩江流域50年的降雨洪水资料分析的结果是一致的。

表4 韩江流域各站洪水同时发生量级组合遭遇概率Table 4 Coincidence risk analysis of flood magnitudes of the three stations %

3.5 条件概率分布及重现期

当韩江潮安站发生大于某一重现期的洪水时，干流梅江横山站和汀江溪口站发生某一量级的洪水的条件概率有多大，对研究韩江流域洪水组成规律的认识和防洪安全等都具有十分重要的价值。表5列出了韩江潮安站发生1000、200、100、50、20、10年一遇洪水时，梅江横山站、汀江溪口站发生各种重现期洪水的条件概率。从表5可以看出，当潮安站发生某一重现期的洪水时，横山、溪口分别发生低重现期洪水的可能性与发生高重现期洪水的可能性非常接近，低重现期洪水的可能性略大;横山站发生各种重现期洪水的条件概率比溪口站要大，如潮安发生1000、200、100、50、20、10 a一遇洪水时，横山站发生同频率的洪水的条件概率分别为 73.11%、73.18%、73.26%、73.43%、73.96%、74.84%，溪口站发生同频率的洪水的条件概率分别为 46.46%、46.62%、46.83%、47.24%、48.49%、50.60%，这说明，潮安站与横山站洪水遭遇组合的概率比与溪口站遭遇组合的概率要高，说明梅江的洪量占潮安站的比重比汀江大，这与横山站的集雨面积较大，且梅江洪量较大有关。同理可以得到，潮安站发生大于某一重现期的洪水时，横山与溪口站各种重现期洪水同时发生的条件概率以及横山与溪口站各种重现期洪水联合发生 (至少有一个发生)的条件概率，由于篇幅限制此结果未列出。

表5 潮安站和横山、溪口站T年一遇洪水遭遇的条件概率Table 5 Condition probabilities of T-year flood coincidence of Chaoan and Hengshan station，Chaoan and Xikou station %

4 结论

利用Copula函数，构建了韩江流域的韩江潮安站、梅江横山站和汀江溪口站年最大日平均流量的二维和三维联合分布，对其洪水遭遇和条件概率进行分析，主要结论如下:

1)通过构建三大水文站的联合分布，可以获得水文站之间不同流量条件下的概率，以及特定联合重现期和同现重现期下，不同水文站最大日流量的可能组合，对韩江流域的洪水组成规律的认识和防洪安全等具有十分重要的理论与实践价值。

2)三大水文站之间洪水遭遇组合分析表明:相同重现期洪水遭遇组合，潮安与横山遭遇的概率大于潮安与溪口，潮安与溪口遭遇的概率大于横山与溪口;当梅江与汀江同时发生洪水时，韩江潮安站出现大洪水几乎是必然事件。

3)三大水文站之间的条件概率表明:潮安发生1000、200、100、50、20、10 a一遇的条件下，横山站发生同频率的洪水的可能性均超过73.11%，溪口站发生同频率的洪水的可能性在46.46%和50.60%之间，说明梅江的洪量占潮安站的比重比汀江大。

［1］王政祥，张明波.南水北调中线水源与受水区降水丰枯遭遇分析［J］.人民长江，2008，39(17):103－105.

［2］肖天国.金沙江、岷江洪水遭遇分析［J］.人民长江，2001，32(1):30－32.

［3］郭生练，闫宝伟，肖义，等.Copula函数在多变量水文分析计算中的应用及研究进展［J］.水文，2008，(3):1－7.

［4］闫宝伟，郭生练，郭靖，等.多变量水文分析计算方法的比较［J］.武汉大学学报:工学版，2009，42(1):10－15.

［5］陈子燊，刘曾美，路剑飞.广义极值分布参数估计方法的对比分析［J］.中山大学学报:自然科学版，2010，49(6):105－109.

［6］闫宝伟，郭生练，陈璐，等.长江和清江洪水遭遇风险分析［J］.水利学报，2010，41(4):67－73.

［7］冯平，李新.基于Copula函数的非一致性洪水峰量联合分析［J］.水利学报，2013，44(10):1137－1147.

［8］GENEST C，FAVRE A C.Everything you wanted to know about copula modeling but were afraid to ask［J］.Journal of Hydrologic Engineering，2007，12(4):347 ～368.

［9］VANDENBERGHE S，VERHOEST N E C，ONOF C，et al.A comparative copula-based bivariate frequency analysis of observed and simulated storm events:A case study on Bartlett-Lewis modeled rainfall［J］.Water Resource Research，2011，47:W07529.

［10］SUBIMAL G.Modelling bivariate rainfall distribution and generating bivariate correlated rainfall date in neighbouring meteorological subdivisions using copula［J］.Hydrological Process，2010，24:3558－3567.

［11］CHOWDHARY H，ESCOBAR L A，SINGH V P.Identification of suitable copulas for bivariate frequency analysis of flood peak and flood volume data［J］.Hydrology Reaearch，2011，42(2/3):193－215.

［12］ZHANG L，SINGH V P.Bivariate flood frequency analysis using the copula method［J］.Journal Hydrologic Engineering ASCE，2006，11(2):150－164.

［13］KAO S C ，GOVINDARAJU R S.A copula-based joint deficit index for droughts［J］.Journal of Hydrology，2010，380:121－134.

［14］WONG G，LAMBERT M F，LEONARD M，et al.Drought analysis using trivariate copulas conditional on climatic states［J］.Journal of Hydrologic Engineering，2010，15(2):129－141.

［15］刘曾美，陈子燊.区间暴雨和外江洪水位遭遇组合的风险［J］.水科学进展，2009，20(5):619－625.

［16］康玲，何小聪.南水北调中线降水丰枯遭遇风险分析［J］.水科学进展，2011，22(1):44－50.

［17］李俊伟.韩江流域“03.5”与“03.6”暴雨洪水分析［J］.广东水利水电，2005，(1):50－52.

［18］刘树锋，邱静，黄本胜，等.韩江流域可能最大暴雨洪水移置计算［J］.水文，2009，29(1):42－46.

［19］李俊伟.基于小波变换的韩江年径流多时间尺度演变特征分析［J］.广东水利水电，2014，(4):5－10.

［20］NELSON R B.An introduction to Copulas［M］.New York:Springer，1999.

［21］HOSKING J R M，WALLIS J R.Regional frequency analysis:An approach based on L-moments［M］.UK:Cambridge University，1997.

［22］MASSEY J R F J.The Kolmogorov-Smirnov test for goodness of fit［J］.Journal of the American statistical Association，1951，46(253):68－78.

［23］FILLIBEN J J.The probability plot correlation coefficient test for normality ［J］.Technometrics，1975，17(1):111－117.

［24］BOZDOGAN H.Model selection and Akaike's information criterion(AIC):The general theory and its analytical extensions［J］.Psychometrika，1987，52(3):345－370.