溪洛渡大坝混凝土二维应力状态下破坏准则与本构关系试验研究

钟贻辉，冉 璟，秦 勇

（1.中国电建集团成都勘测设计研究院有限公司，四川 成都 610072；2.中交天航港湾建设工程有限公司，天津 300450）

溪洛渡大坝混凝土二维应力状态下破坏准则与本构关系试验研究

钟贻辉1，冉 璟1，秦 勇2

（1.中国电建集团成都勘测设计研究院有限公司，四川 成都 610072；2.中交天航港湾建设工程有限公司，天津 300450）

采用溪洛渡水电站拱坝混凝土施工配合比，进行二维应力状态下（压—压、拉—压、拉—拉），实际拱坝混凝土的破坏准则与本构关系研究。根据试验结果，并结合已有二维应力状态下混凝土的破坏准则与本构关系研究模型，建立了适用于该工程拱坝混凝土二维应力状态下的破坏准则模型与本构关系。

二维应力状态；高拱坝；破坏准则；本构关系；大坝混凝土；应力空间

0 前 言

拱坝在运行过程中，大坝混凝土的受力大部分处于二维或三维应力状态下。目前，我国的《拱坝设计规范》仍然采用大坝混凝土的湿筛小试件单轴抗压强度作为抗压强度设计指标，只是在设计过程中，根据设计经验，考虑了并不统一的安全系数来进行计算，而根本没有确切的掌握大坝混凝土具体部位的真实强度。这种设计方法因涉及到取用安全系数的数值为经验数据，有可能造成拱坝在运行过程中某些部位的混凝土强度偏于安全，而某些部位的混凝土强度不能满足设计要求的强度，偏于危险。

考虑到实际大坝混凝土是在复杂应力状态下运行，国外学者在这方面进行过较多的研究，并获得过不少的研究成果，如Bresler－Pister［1］和Willam－Warnke［2］的三参数模型、Ottosen［3］和Hsieh－Ting－Chen［4］的四参数模型、Kotsovos［5］和Podgorski［6］五参数模型等。目前国外的很多国家，如日本、俄罗斯、英国、美国等的设计规范均引入了混凝土的双轴强度准则。近年来，国内的中国水电顾问集团成都勘测设计研究院科研所［7］、中国水利水电科学研究院［8］、清华大学［9］、大连理工大学［10］等单位较早地开展了这方面的研究，并提出了不同形式的混凝土破坏准则，一般认为四参数和五参数模型的精度最好。

纵观国内目前对混凝土二维与三维应力状态下的破坏准则与本构关系研究成果，多非针对水电工程实际，特别是对特大型水电工程，如300 m级的高拱坝混凝土，而恰恰高拱坝在运行过程中处在复杂应力状态下工作的大坝混凝土部位较多，且各大、特大型水电工程由于均采用了当地的人工骨料作为混凝土骨料，而不同骨料品种表现出来的混凝土特性有很大的不同［11］，因此，针对特大型工程的大坝混凝土实际，非常有必要进行专门的复杂应力状态下的大坝混凝土破坏准则与本构关系研究。

本文结合溪洛渡水电工程的拱坝混凝土，开展了二维应力状态下的大坝湿筛混凝土的破坏准则与本构关系试验，结合试验成果与国内已有的二维应力状态下混凝土的破坏准则与本构关系模型，给出了适合于本工程大坝混凝土在二维应力状态下的破坏准则与本构关系计算模型。

1 试验条件

1.1 试验用配合比

本次试验采用了工程目前大坝混凝土施工用配合比，主要配合比参数及原材料品种见表1。

1.2 试件尺寸

本次试验涉及到大坝混凝土的单轴抗拉与抗压、双轴压—压／拉—压／拉—拉试验，以上试验用试件均采用1003mm3的尺寸。

2 试验结果

拉—拉应力状态下的强度试验结果见表2，压—压应力状态下的强度试验结果见表3，拉—压应力状态下的强度试验结果见表4，双轴与单轴的变形性能试验结果见表5。表中“T”表示拉应力（以正值表示），“C”表示压应力（以负值表示）。

表1 主要配合比参数与原材料品种

表2 拉—拉应力状态下混凝土的强度

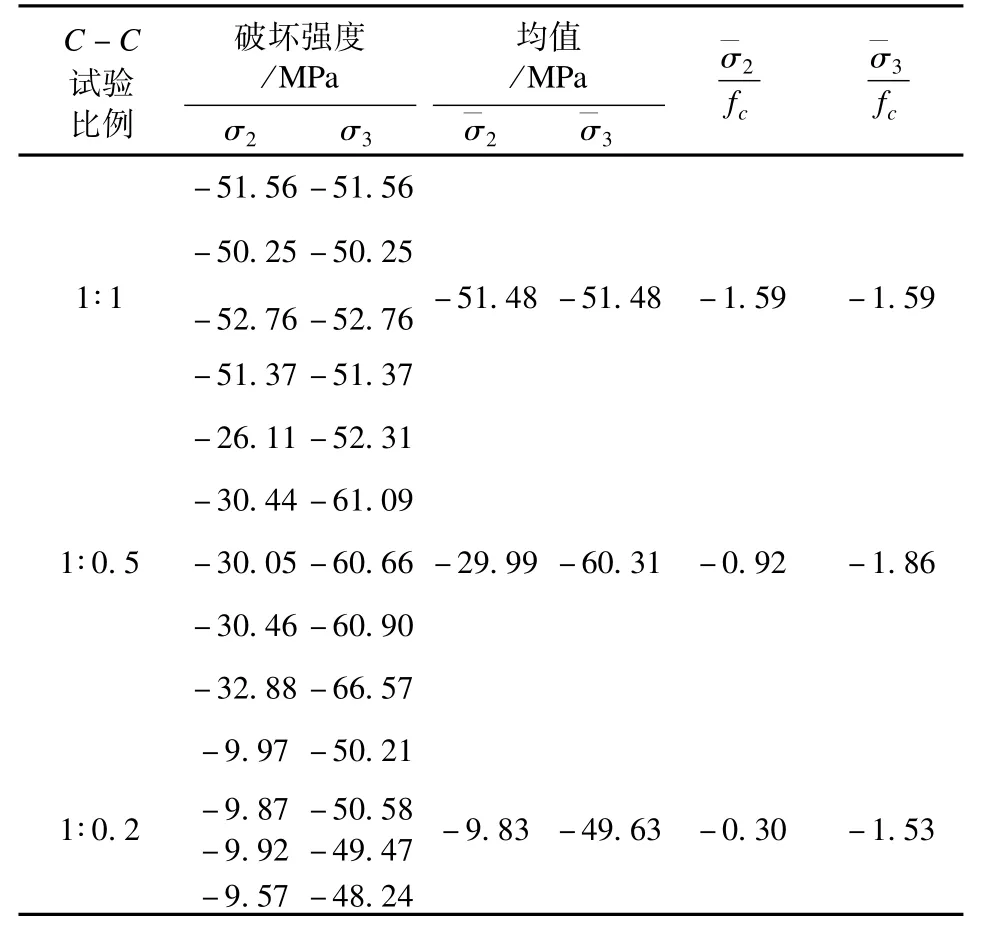
表3 压—压应力状态下混凝土的强度

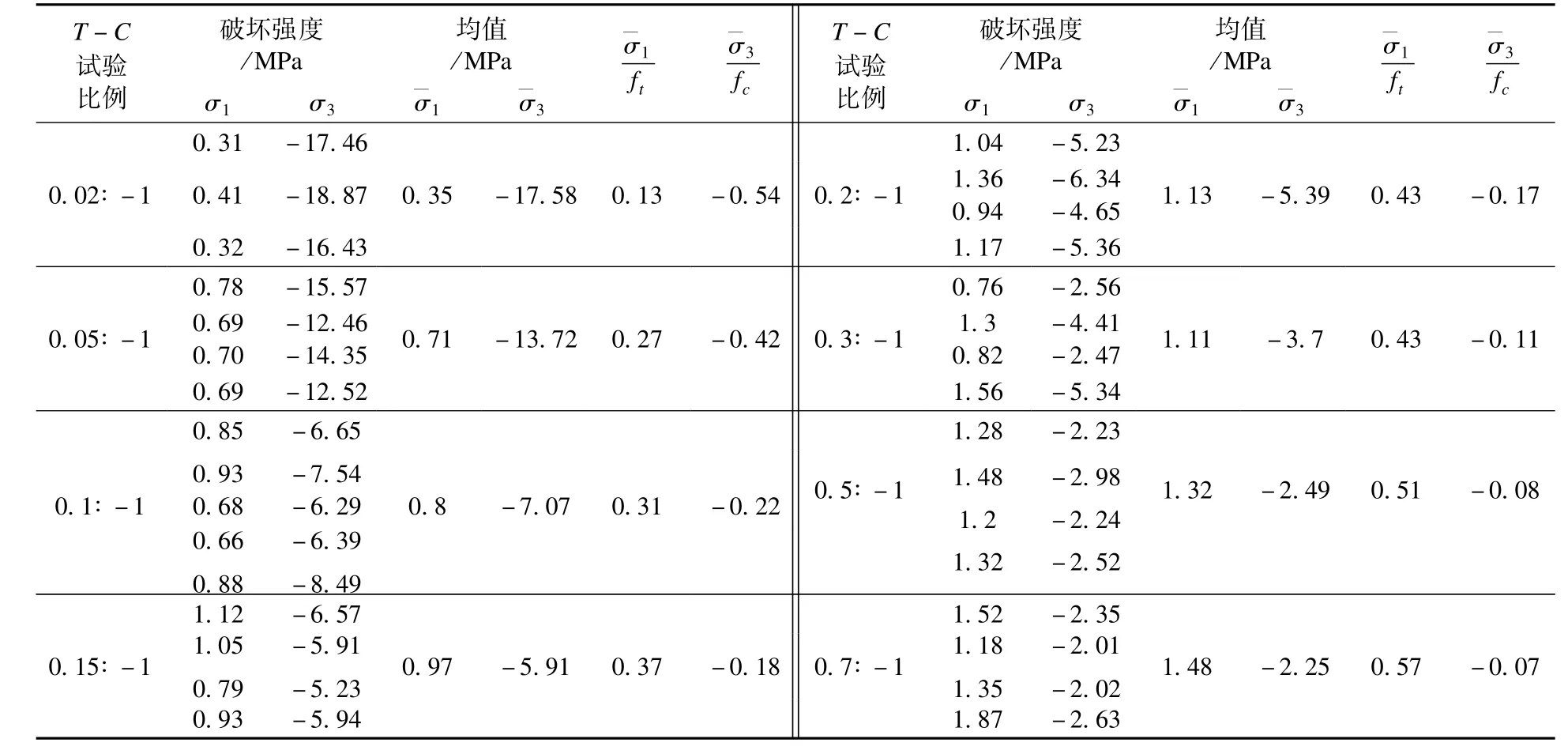
表4 拉—压应力状态下混凝土的强度

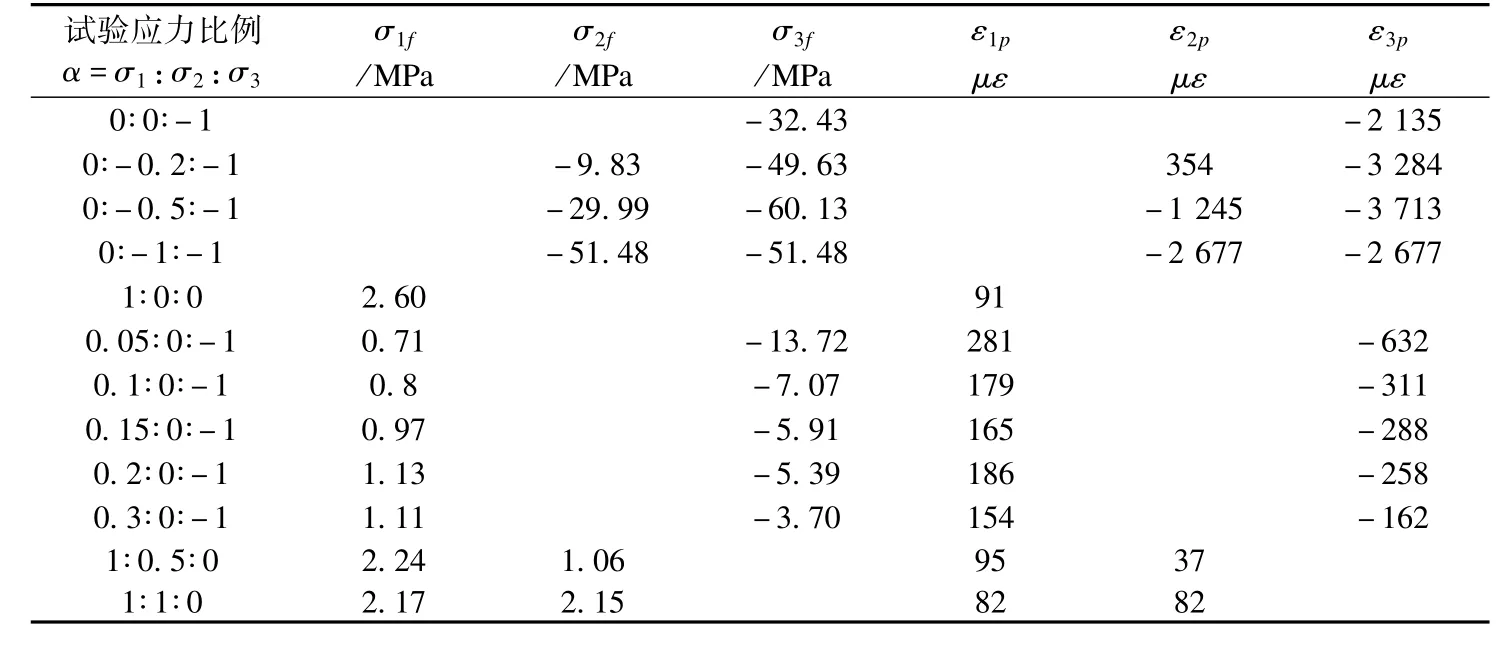
表5 双轴受力状态下不同应力比对应的强度和极限应变

3 二维应力状态下大坝混凝土的破坏准则

3.1 双轴压—压破坏准则

以往的研究表明，按Kupfer准则［12］建立的主应力空间下混凝土双轴压强度准则与试验吻合较好，本文亦借用Kupfer准则（如式1所示）进行压—压应力状态下的试验值拟合。

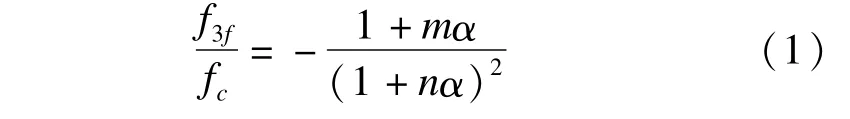
式中 f3f——为双轴抗压强度；

fc——为单轴抗压强度平均值；

按Kupfer准则与表3中的试验数据，对本次试验数据进行拟合的结果如下式所示：

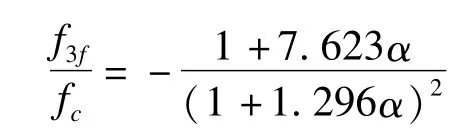
3.2 双轴拉—压破坏准则

综合以往研究成果的优劣［12－14］，本次试验按椭圆曲线（如式2所示）来确定主应力空间下双轴拉压状态的破坏准则：

式中 ft——为单轴抗拉强度平均值；fc——为单轴抗压强度平均值；

A、B、C、D、E——为待回归的系数。

据表4的试验结果，经拟合后拉－压应力状态下的破坏准则如下式所示：

3.3 双轴拉－拉破坏准则

研究成果表明［15］，在双轴拉状态下，近似认为双轴拉强度与单轴拉强度相同，且与应力比无关。分析试验结果和混凝土多相复合材料的弱点，如非匀质、具有微裂缝、离散性大等，可以得出结论：双轴抗拉强度低于单轴抗拉强度。因为多向受拉时，混凝土各向的缺陷都会得到反映，开裂的可能性会增大。因此建立如下的双轴受拉破坏准则（如式3所示）：

ft——为单轴抗拉强度；

a与b——为待回归系数。根据试验结果，得出本次拉—拉应力状态下的破坏准则：

3.4 小 结

二维应力状态下大坝湿筛混凝土的破坏准则拟合曲线见图1。

图1 大坝湿筛混凝土二维应力状态下破坏准则拟合曲线

4 二维应力状态下大坝混凝土的本构关系

4.1 压—压应力状态下混凝土的峰值应变

双轴压—压试件破坏时的主应变ε2p和ε3p随应力比α变化见图2。

图2 双轴压—压下峰值应变与应力比的关系

经拟合后得出如下模型：

式中ε3p，ε2p为单轴受压时主轴与副轴对应的峰值应变。

4.2 拉—压应力状态下混凝土的峰值应变

拉—压应力状态下，主拉应变ε1p与平均应力σm具有较高的相关性，主压应变ε3p与比值σ3p／fc的函数具有较好的相关性，如图3所示。

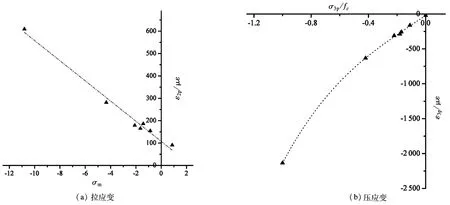
图3 拉—压应力状态下极限应变与平均应力的关系

对拉压受力状态下极限应变值的回归方程如下所示：

式中，平均应力σm＝（σ1＋σ2＋σ3）／3，r是相关系数。

4.3 拉—拉应力状态下混凝土的峰值应变

双向受拉应力状态下，试件二轴拉伸应力－应变曲线与单轴拉伸曲线相似。试件发生拉断破坏，曲线非常陡，而且极限应变值很小。实测峰值应变ε1p、ε2p随应力比α＝σ2／σ1的变化规律如图4所示。

图4 双轴拉—拉下极限应变与应力比的关系

经回归得到如下极限应变表达式：

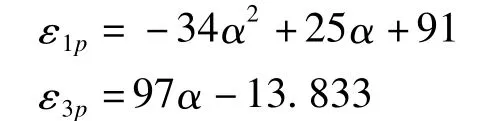
4.4 二维应力状态下大坝混凝土的本构关系模型与拟合曲线

在二维应力状态下，按过镇海［15］提出的非线弹性正交各向异性—增量型模型进行拟合，模型如公式4所示。

式中 σ1、σ2、σ3——为主应力；

ε1、ε2、ε3——为主应变；

E1、E2、E3——为主应力方向的弹性模量；vij（i，j＝1，2，3）——为j方向应力在i方向产生的横向效应（泊松比）。

根据多维应力状态下混凝土的本构关系模型（式4），对二维应力状态下的不同受力组合进行不同形式的公式处理后，再依据试验成果，按理论模型拟合后，发现模型与试验成果吻合较好。不同二维应力状态下，典型的拟合关系曲线如图5所示。

图5 不同二维应力状态下大坝混凝土本构关系拟合曲线

5 结 语

本次试验结合溪洛渡工程实际，开展了二维应力状态下压—压、拉—压与拉—拉应力组合的强度与变形性能试验，并拟合得出了适用于溪洛渡工程大坝混凝土的破坏准则模型、峰值应变模型，可供类似工程借鉴。

［1］ C.J.Bellamy.Strength of concrete under combined stress［J］. ACI JL58－18：367－382.

［2］ W illam K J，Warnke E P.Constitutive models for the triaxial behavior of concrete［J］.IABSE Proceeding，Italy，1975，19：1－30.

［3］ Niels Saabye Ottosen.A failure criterion for concrete.Journal of Engineering［J］.Mechanics Division.ASCE，1977，103（EM 4）：527－535.

［4］ Hsieh S S，Ting E C，Chen W F.An Elastic－Fracture Model for Concrete.Proceeding of 3nd Engineering Mechanics Division［J］. Special Conference ASCE，Austin，1979：437－440.

［5］ Kotsovos M D.A mathematical description of the strength properties of concrete under generalized stress［J］.Magazine of Concrete Research，1979，31（108）：151－158.

［6］ Podgorski J.General failure criterion for isotropic Media［J］. Journal of Engineering Mechanics Asce，1985，111（EM 2）：188－201.

［7］ 李嘉进.混凝土容许应力研究［J］.水电站设计，1992（2）.

［8］ 杨木秋.混凝土二轴受压与二轴拉压强度及其在拱坝设计中的应用［J］.人民长江，1992（6）.

［9］ 过镇海，王传志，张秀琴等.混凝土的多轴强度试验和破坏准则研究.北京：清华大学出版社，1996.

［10］ 宋玉普.多种混凝土材料的本构关系和破坏准则［M］.北京：中国水利水电出版社，2002.

［11］ 钟贻辉，等.原材料参数对喷射纤维混凝土弯拉韧度的影响［J］.水电站设计，2008，24（3）.

［12］ Halmut B.Kupfer，Kurt H.Gorstle.Behavior of concrete under biaxial stress［J］.F.ASCE，1973，99（4）：853－866.

［13］ 彭放.复杂应力状态下多种混凝土的破坏准则及本构模型研究［D］.大连：大连理工大学博士学位论文，1990.

［14］ 宋玉普，赵国藩等.多轴应力下多种混凝土材料的通用破坏准则.土木工程学报，1996，29（1）：25－32.

［15］ 过镇海.混凝土的强度和变形试验基础和本构关系［M］.北京：清华大学出版社，1997.

简讯

成都院再添3项发明专利

日前，成都院申请的“地下洞室顶拱塌方后的衬砌处理方法”等3项发明专利获国家知识产权局授权，并于近日收到专利证书。

发明专利“地下洞室顶拱塌方后的衬砌处理方法”，公开了一种地下洞室顶拱塌方后的衬砌处理方法，涉及地下洞室施工领域，提供一种工作量小、成本低、防塌效果好的地下洞室顶拱塌方后的衬砌处理方法。本发明可用于修复塌方的地下洞室。

“定量化评价超大型地下洞室群施工期围岩稳定性的方法”，提供了一种有效的定量化评价超大型地下洞室群施工期围岩稳定性的方法，从而能够获得直观准确的稳定性判断数据，以控制围岩稳定，保障工程顺利建设和长期安全稳定运行。

“大型地下洞室群布置方法”，公开了一种在水利水电工程、地下储库工程运用的大型地下洞室群布置方法，该方法可全面考虑影响地下洞室围岩稳定的主要因素，特别是岩石强度应力比这一至关重要因素，使大型地下洞室群设计方案更为科学，考虑的因素更为全面。

（本刊编辑部）

TV431

B

1003－9805（2015）02－0064－06

2014－06－23

钟贻辉（1982－），男，四川宜宾人，工程师，从事水工混凝土性能研究工作。