Q235冷弯薄壁等边角钢压杆承载力计算方法★

赵胜江 林 灏 吕 呈 孙德发

(1.嘉兴学院，浙江 嘉兴 314001； 2.桐乡市亚都钢业有限公司，浙江 桐乡 314500； 3.嘉兴学院结构工程研究所，浙江 嘉兴 314001)

Q235冷弯薄壁等边角钢压杆承载力计算方法★

赵胜江1林 灏2吕 呈1孙德发3

(1.嘉兴学院，浙江 嘉兴 314001； 2.桐乡市亚都钢业有限公司，浙江 桐乡 314500； 3.嘉兴学院结构工程研究所，浙江 嘉兴 314001)

在分析比较GB50018—2002冷弯薄壁型钢结构技术规范条文规定的基础上，结合试验结果，对Q235冷弯薄壁等边角钢压杆承载力计算方法进行了较深入的探讨和分析比对，研究结果显示：采用有效宽度法的国内现行规范GB50018—2002可以有效地预测Q235冷弯薄壁等边角钢压杆的稳定承载力，与试验结果吻合良好且偏于安全。

冷弯薄壁型钢，等边角钢，压杆，有效宽度法，极限承载力

冷弯薄壁型钢作为一种可重复利用的环保型建筑材料，已经被大量使用在轻型钢结构体系中，如低层住宅、工业厂房、钢模板、脚手架、桥梁结构、输电线塔等。冷弯型钢构件用相对较少材料承受较大的外载，不是单纯的增大截面面积，而是通过改变截面形状的方法获得。角钢截面广泛应用于塔架结构、格构柱、桁架结构及支撑结构等。

冷弯薄壁等边角钢截面属于单轴对称开口截面，压杆失稳有整体屈曲和局部屈曲两种模式。可能对最小主轴弯曲屈曲，也可能对对称轴弯扭屈曲；可能局部屈曲，也可能畸变屈曲；还可能发生既有整体屈曲又有局部屈曲。从GB 50018—2002冷弯薄壁型钢结构技术规范[1]第5.2.3条规定可以看出，计算截面全部有效的不卷边的等边单角钢轴心受压构件，只考虑了弯曲屈曲，并没有考虑弯扭屈曲和局部屈曲等形式。如果计算截面不是全部有效怎么办，究竟哪种失稳模式起控制作用，目前还无法找到合适的解释。针对上述问题，本文将在L30×2.0截面Q235冷弯薄壁等边角钢压杆承载力试验的基础上，结合GB 50018—2002冷弯薄壁型钢结构技术规范中的计算方法进行理论计算与分析比对，以期寻出规律，为此类设计提供参考。

1 试验

冷弯薄壁等边角钢截面尺寸为L30×2.0，压杆试件长度分别为300 mm，500 mm和1 000 mm。截面特性见表1，符号定义见图1。试件加载装置[2]和试件布置示意图见图2。试件试验承载力见表2。试件材料为Q235，理论计算取fy=235 N/mm2，f=205 N/mm2，E=206 000 N/mm2。

表1 截面特性

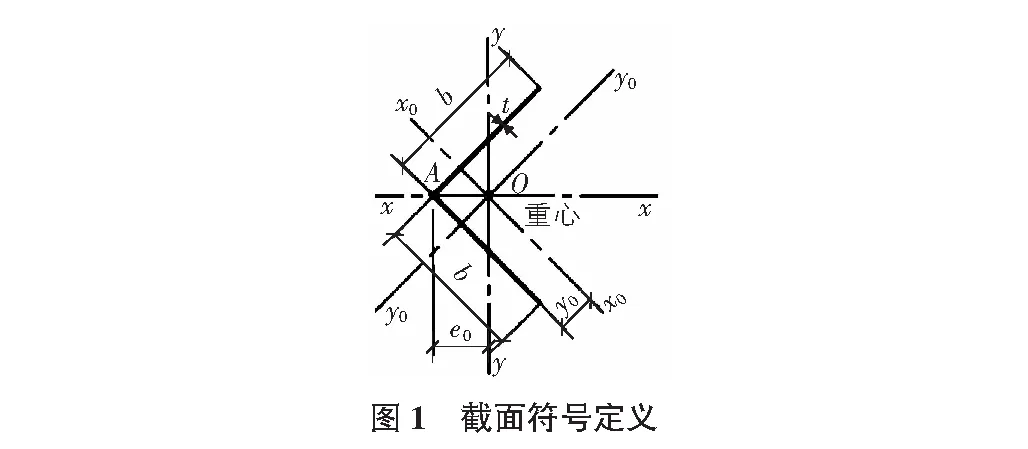
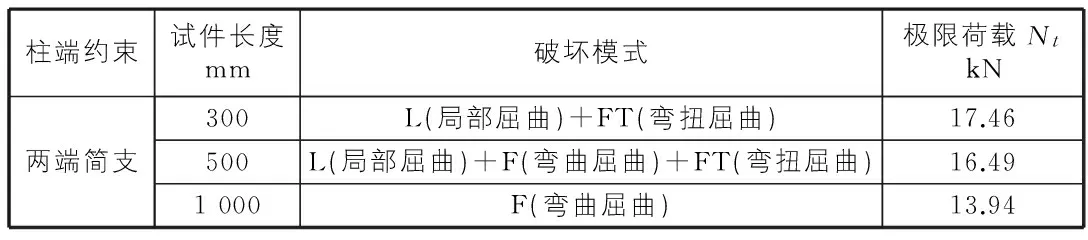
表2 试件试验承载力

2 理论计算

2.1 按GB 50018—2002第5.2.3条的规定

考虑弯曲屈曲，假定截面全部有效，计算Q235冷弯薄壁等边角钢压杆稳定系数时，其长细比取下式算得的较大值:

(1)

(2)

其中，λx，λy分别为构件对截面主轴x轴和y轴的长细比；lox，loy分别为构件在垂直于截面主轴x轴和y轴的平面内的计算长度；ix，iy分别为构件毛截面对其主轴x轴和y轴的回转半径。

2.2 按GB 50018—2002第5.2.4条的规定

考虑弯扭屈曲，按照单轴对称开口截面来计算Q235冷弯薄壁等边角钢压杆稳定系数时，其长细比应该取式(2)和下式算得的较大值:

(3)

(4)

(5)

其中,λw为弯扭屈曲的换算长细比；Iw为毛截面扇形惯性矩；It为毛截面抗扭惯性矩；e0为毛截面的弯心在对称轴上的坐标；lw为扭转屈曲的计算长度，lw=β·l，l为无缀板时，取构件的几何长度，有缀板时，取两相邻缀板中心线的最大距离；α，β均为约束系数。考虑截面全部有效，不同整体屈曲模式下的冷弯薄壁等边角钢压杆的稳定承载力N=φAf，见表3。

2.3 按GB 50018—2002第5.6条的规定

对于非加劲板件，有效宽度按下式计算:

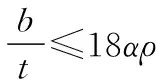
(6)

(7)

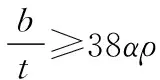
(8)

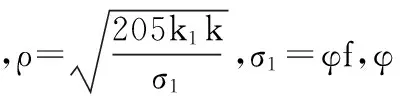
考虑整体—局部屈曲相关性(有效截面问题)下的冷弯薄壁等边角钢压杆的稳定承载力N=φAef，见表4。

表4 试件稳定承载力(二)

3 比较分析

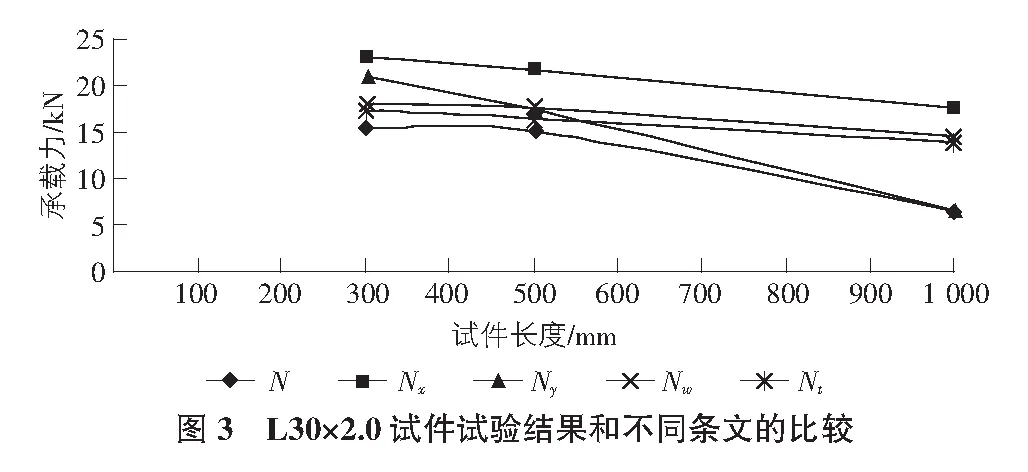
按GB 50018—2002冷弯薄壁型钢结构技术规范不同条文规定计算的两端简支冷弯薄壁等边角钢压杆(L30×2.0)极限承载力与试验结果比较见图3。其中N为考虑整体—局部屈曲相关性(有效截面问题)下的冷弯薄壁等边角钢压杆的稳定承载力；Nx为考虑截面全部有效，对x轴弯曲屈曲模式下的冷弯薄壁等边角钢压杆的稳定承载力；Ny为考虑截面全部有效，对y轴弯曲屈曲模式下的冷弯薄壁等边角钢压杆的稳定承载力；Nw为考虑截面全部有效，对x轴弯扭屈曲模式下的冷弯薄壁等边角钢压杆的稳定承载力；Nt为冷弯薄壁等边角钢压杆的试验承载力。从图3来看，对于两端简支的试件，只有考虑整体—局部屈曲相关性(有效截面问题)下的冷弯薄壁等边角钢压杆的稳定承载力N小于试验承载力Nt，说明此计算方法是安全的。考虑截面全部有效，当长细比较小时，弯扭屈曲承载力Nw小于弯曲屈曲承载力Ny，说明按GB 50018—2002第5.2.3条的规定计算将会导致不安全。综上所述，对Q235冷弯薄壁等边角钢轴压杆承载力计算既要考虑有效截面，又要考虑弯扭屈曲。

4 结语

结果表明：采用GB 50018—2002冷弯薄壁型钢结构技术规范中的有效宽度法可以有效地预测Q235冷弯薄壁等边角钢压杆的稳定承载力，与试验结果吻合良好且偏于安全。

[1] GB 50018—2002，冷弯薄壁型钢结构技术规范[S].

[2] 周鹏杰，冷 光，孙德发.冷弯薄壁卷边槽钢轴压柱承载力的计算方法[J].山西建筑，2011，37(6)：25-27.

Calculation method for load-carrying capacity of Q235 cold-formed thin-wall equal angle members under axial compression★

Zhao Shengjiang1Lin Hao2Lv Cheng1Sun Defa3

(1.JiaxingCollege,Jiaxing314001,China; 2.TongxiangYaduSteelIndustryCo.,Ltd,Tongxiang314500,China; 3.InstituteofStructuralEngineering,JiaxingCollege,Jiaxing314001,China)

Based on the contrast analysis ofTechnicalCodeofCold-FormedThin-WallSteelStructure(GB 50018—2002)， analysis and discussion are mentioned about the ultimate load-carrying capacities of Q235 cold-formed thin-wall equal angle members under axial compression combined with the test results. The results showed that， it is valid and relative safety for prediction the ultimate load-carrying capacities of Q235 cold-formed thin-wall equal angle members under axial compression according to the effective width method for technical code of cold-formed thin-wall steel structure(GB 50018—2002).

cold-formed steel, equal angle steel, axial compression member, effective width method, ultimate load

2015-06-04★：嘉兴学院重点SRT项目(项目编号：851714030)

赵胜江(1993- )，男，在读本科生； 林 灏(1984- )，男，助理工程师； 吕 呈(1993- )，男，在读本科生； 孙德发(1969- )，男，副教授

1009-6825(2015)23-0023-02

TU392.1

A