一类环长至少为10的准循环LDPC码

范文同，马林华，林志国，邹浩彦，田 雨

(1.空军工程大学 a.航空航天工程学院； b.装备管理与安全工程学院, 陕西 西安 710051;

一类环长至少为10的准循环LDPC码

范文同1a，马林华1a，林志国1b，邹浩彦2，田 雨3

(1.空军工程大学 a.航空航天工程学院； b.装备管理与安全工程学院, 陕西 西安 710051;

2.中国人民解放军驻西安飞机工业公司军事代表室,陕西 西安710089; 3.中国人民解放军95876 部队, 甘肃 张掖 734100)

为扩展性能优良、易于工程实现的LDPC码的构造方法，提出了一类环长至少为10的准循环低密度奇偶校验码的构造方法。该方法首先基于基矩阵和2m准则构造出环长至少为10的校验矩阵；然后，利用掩蔽矩阵对得到的校验矩阵进行变换；最终，构造出满秩的准循环LDPC码。理论分析和仿真结果表明，该类QC-LDPC码字构造灵活，在AWGN信道下具有优异的性能。

通信；环长；满秩；准循环低密度奇偶校验码

1 准循环LDPC码

低密度奇偶校验码[1](LDPC)是Gallager于1962年提出的一种线性纠错编码方案，因其具有接近香农限的优异性能，现已被诸多通信标准所采纳并应用[2-4]。LDPC码构造是其应用的基础。随机构造的码字性能优异，但往往编解码复杂，难以在实际工程中应用。构造易于工程实现且性能优异的LDPC码成为研究的重点方向。

准循环LDPC码具有结构化的特点，相较于随机构造的LDPC码，其校验矩阵构造简单，易于存储，编解码算法复杂度低，工程上易于实现，且通过设计可以构造出性能优异的码字，因而得到了广泛的研究[5-14]。通过循环置换矩阵构造准循环LDPC码是一种常用的构造方法。文献[11]给出了此方法构造码字的一类框架，分析了构造原理，但此方法构造出的校验矩阵不满秩；文献[12]提出了一类基矩阵，基于最大公约数思想构造环长至少为8的准循环LDPC码，并给出了具体的掩蔽矩阵使校验矩阵满秩，但未给出掩蔽矩阵的构造原理；文献[13]研究了构造列重较大的环长至少为8的准循环LDPC码的方法，也未说明如何构造使校验矩阵满秩的掩蔽矩阵；文献[14]提出了两种构造环长至少为10的LDPC码的方法，但仅限于列重为3的情况，且构造出的码字不具有严格的准循环特性。

2 环及环长

(N,K)LDPC码可以由校验矩阵H表示，N表示码字长度，K表示信息位长度。校验矩阵中含有不同长度的环[1]，任一 LDPC 码的校验矩阵所含环的环长至少为4，且均为偶数。短环的存在会加速错误信息的传播，导致译码发散和错误，构造大环长的LDPC码通常能够获得比用同等构造方法构造的短环LDPC码更高的信噪比增益。

结合本文构造方法需要，以下列出了校验矩阵中不同环长对应的停止集。校验矩阵中长度为4的环表现形式如图1所示，则围长至少为6的LDPC码的校验矩阵中不含图1所示的环。

图1 环长为4的停止集

校验矩阵中长度为6的环表现形式如图2所示，则围长至少为8的LDPC码的校验矩阵中不含图1和图2所示的环。

图2 环长为6的停止集

校验矩阵中长度为8的环表现形式较多，本文只列出其中一部分，如图3所示。在构造围长至少为10的LDPC码时，应避免其校验矩阵中含图1、图2或图3所示的环。

图3 环长为8的部分停止集

3 本文构造方法

定义矩阵

(1)

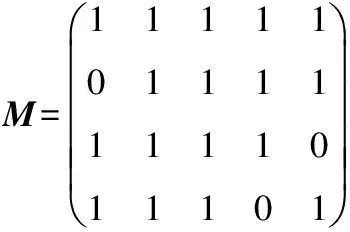
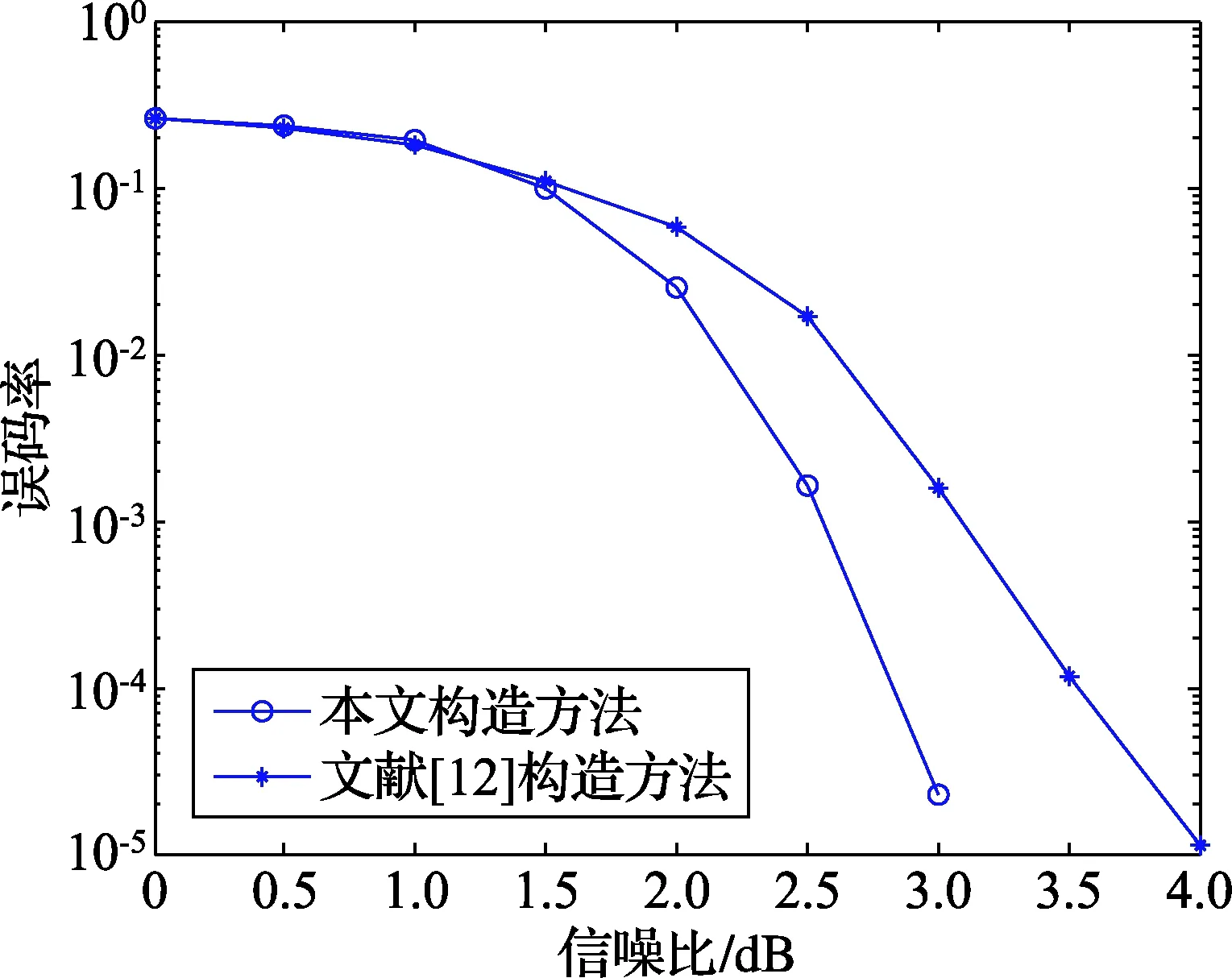
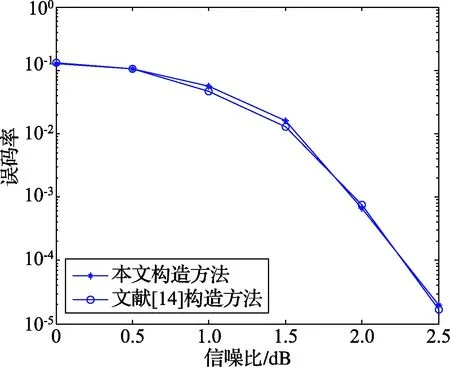
式中：J，L均为正整数，且J≥3，L≥3；a0,a1,…,aL-1为满足 0≤a0

将矩阵中ai·j(i=0,…,L-1;j=0,…,J-1)转换为大小为P×P的循环置换矩阵I(ai·j)，ai·j(modP)为单位阵I循环右移的位置。转换后得到的新矩阵表示为

(2)

式中：pj,i=ai·j(0≤j≤J-1,0≤i≤L-1)。

维数为J×L的矩阵H即为本文设计的校验矩阵，矩阵E称为校验矩阵H的基矩阵。

文献[11]中给出了LDPC码校验矩阵中含有环长为2m(m>1)的环的条件，由此可得定理1。

定理1：准循环LDPC码的校验矩阵H包含环长为2m的环的充分必要条件是

(3)

式中:0≤jk≤J-1，jk≠jk+1，jm=j0，0≤ik≤L-1。

依据此定理，式(2)所示的准循环LDPC码的校验矩阵的环长至少为10的充分必要条件是

ai0j0-ai0j1+ai1j1-ai1j0≠0(modP)

(4)

ai0j0-ai0j1+ai1j1-ai1j2+ai2j2-ai2j0≠0(modP)

(5)

ai0j0-ai0j1+ai1j1-ai1j2+ai2j2-ai2j3+

ai3j3-ai3j0≠0(modP)

(6)

式中:0≤j0,j1,j2,j3≤J-1,0≤i0,i1,i2,i3≤L-1。

式(4)保证了校验矩阵中无环长为4的环，式(5)保证了无环长为6的环，式(6)保证了无环长为8的环。因此，通过式(4)～式(6)构造的准循环LDPC码的校验矩阵的环长至少为10。

综上所述，本文给出搜索S={a0,a1,…,aL-1}的具体步骤如下：

步骤1),初始化S={a0}，a0为非负整数，i=0。

步骤2),令Y=ai。

步骤3),令Y=Y+1，k=0,…,i，ai+1=Y，代入式(1)，计算E(a0,…,ai,ai+1)是否满足式(4)，若满足，则表明其中不含4环，执行下一步骤；若不满足，则表明其中含4环，重复步骤3)。

步骤4),计算E(a0,…,ai,ai+1)是否满足式(5)，若满足，则表明其中不含6环，执行下一步骤；若不满足，则表明其中含6环，跳转至步骤3)。

步骤5),计算E(a0,…,ai,ai+1)是否满足式(6)，若满足，则表明其中不含8环，执行下一步骤；若不满足，则表明其中含8环，跳转至步骤3)。

步骤6),S=S∪Y，i=i+1。若i

给定参数J,L,a0，通过上述搜索算法可以得到本文的基矩阵参数a0,a1,…,aL-1，进而由式(2)构造出环长至少为10的准循环LDPC码。由搜索过程可知，矩阵参数a0,a1,…,aL-1不是唯一的，也说明构造方法是灵活的。

通过上述方法构造的准循环LDPC码不是满秩的，实际上，通过循环置换矩阵构造的码字都存在这样的问题[11-13]。为使H满秩，常用的方法是设计掩蔽矩阵M，M和E(a0,…,aL-1)具有相同的维数，M中的0元素对应的H中相应位置用P×P的全0阵替代，其余不变。经此变换后得到的校验矩阵H′满秩，且满足环长至少为10。

定理2：掩蔽矩阵M满秩是H′满秩的必要条件。

证明：假设M为非满秩矩阵，不失一般性，令M中第i行和第j行之和等于第k行。由M和H′的对应关系可知H′中第(i-1)P+1行至第iP行，第(j-1)P+1至jP行之和，等于(k-1)P+1行至第kP行之和，H′不满秩。因此，M满秩是H′满秩的必要条件。得证。

由此，在构造LDPC码时，首先根据本文前述方法构造出如式(2)所示的校验矩阵；然后，构造满秩矩阵M，M的维数通常较小，易于构造；最后，用M对校验矩阵进行掩蔽，并检测新矩阵是否满秩，若不满秩则重新构造满秩矩阵M。

4 仿真结果与分析

例1：取J=4,L=5,P=300，掩蔽矩阵M如式(7)，构造出N=1 500,K=300的环长至少为10的满秩准循环LDPC码。与文献[12]构造的J=4,L=5,P=300，即同等码长、码率的环长至少为8的满秩准循环LDPC码字的性能比较如图4所示。仿真中均采用BP译码算法[15]，最大迭代次数均设置为100次。

(7)

图4 本文构造方法与文献[12]构造方法性能比较

例2：取J=3,L=5,P=155，掩蔽矩阵M如式(8)，构造出N=775,K=465的环长至少为10的满秩准循环LDPC码。与文献[14]构造的J=3,L=5，N=775,K=459，环长至少为10的LDPC码字的性能比较如图5所示。仿真条件同上。

(8)

图5 本文构造方法与文献[14]构造方法性能比较

图4显示本文构造的码字性能明显优于文献[12]构造的码字性能，主要是本文构造的码字环长至少为10，而后者最小环长为8。由此也可以看出环长对码字的性能有影响。图5显示本文构造的码字与文献[14]构造的码字性能相当，两者均是环长至少为10的LDPC码，然而文献[14]构造出的码字并不是严格准循环的，这在实际应用中会增加译码复杂度。

为进一步对比本文构造的准循环码字与非严格准循环码字的译码复杂度，基于例2中本文和文献[14]构造的2种码字，在Altera Stratix II EP2S60F1020I4芯片上，通过Verilog编程、ModelSim仿真，实现译码器的硬件仿真，译码器资源消耗及处理时延如表1所示。

表1 两种方法构造的码字的译码复杂度对比

方法ALUT/个内存/bit迭代一次所需时钟周期文献[14]862457367136本文算法658340269112

从表中可以看出，本文方法构造的准循环码字无论在资源消耗还是处理时延上均优于文献[14]中构造的非严格准循环码字，即本文方法构造的码字更易于工程实现。

5 小结

本文在前人研究的基础上，提出了一类环长至少为10的满秩准循环LDPC码构造方法，仿真表明该类码字性能优异。本文的构造方法进一步扩展了LDPC优良码字的可选择性，具有一定的工程应用价值。

[1] GALLAGER R G. Low-density parity-check codes[J]. IRE Trans. Information Theory，1962，8(1)：21-28.

[2] ANDREWS K S, DOLINAR S, JONES R.The development of turbo and LDPC codes for deep-space applications[C]// Proc. the IEEE Conference.[S.l.]：IEEE Press，2007， 95(11)：2142-2156.

[3] Draft ETSI EN 302 307 V1.1.1， European standard (telecommunication series) Digital Video Broadcasting (DVB)[S].1997.

[4] CCSDS 131.0-P-1.1， Consultative Committee for Space Data Systems(CCSDS)，tm synchronization and channel coding， draft recommendation for space data system standard[S].2012.

[5] LI Lixin， ZHU Meng， YANG Fan. Performance analysis of QC-LDPC construction based on distance graph[C]//Proc. 2013 IEEE 8th Conference on Industrial Electronics and Applications (ICIEA). [S.l.]：IEEE Press，2013：1162-1166.

[6] ZHANG Jianjun，DONG Mingke，JIN Ye. A QC-LDPC construction algorithm for increasing the throughput of layered decoders[C]//Proc. 2013 15th IEEE International Conference on Communication Technology. [S.l.]：IEEE Press，2013：604-608.

[7] HAN Guojun，GUAN Yongliang，KONG Lingjun. Construction of irregular QC-LDPC codes via masking with ACE optimization[J]. IEEE Commun. Letters，2014，18(2)：348-351.

[8] CHEN Zhixiong，YUAN Jinsha. Construction of structure LDPC codes with full rank based on multi-permutation matrix[J]. ACTA Electronica Sinica，2012，40 (2)：313-318.

[9] ALEXANDER G， MICHAEL H. Low-density parity-check codes from transversal designs with improved stopping set distributions[J]. IEEE Trans. Commun.，2013，61(6)：2190-2200.

[10] DAVID G M M，ROXANA S， DANIEL J C. Quasi-cyclic LDPC codes based on pre-lifted protographs[J]. IEEE Trans. Inf. Theory，2014，60(10)：5856-5874.

[11] FOSSORIER M P C. Quasi-cyclic low-density parity-check codes from circulant permuation maries[J]. IEEE Trans. Inf. Theory，2004，50(8)：1788-1793.

[12] ZHANG Guohua，SUN Rong，WANG Xinmei. Construction of girth-eight QC-LDPC codes from greatest common divisor[J]. IEEE Commun. Letters，2013，17(2)：369-372.

[13] ZHANG Jianhua，ZHANG Guohua. Deterministic girth-eight QC-LDPC codes with large column weight[J]. IEEE Commun. Letters，2014，18(4)：656-659.

[14] WANG Juhua，ZHANG Guohua，ZHOU Quan， et al. Explicit constructions for type-1 QC-LDPC codes with girth at least ten[J]. IEEE Information Theory Workshop， 2014(6)：436-440.

[15] RICHARDSON T J， URBANKE R. The capacity of low-density parity check codes under message passing decoding[J]. IEEE Trans. Inf. Theory， 2001，47(1)：599-618.

范文同(1983— )， 博士生，主研协同通信；

马林华(1963— )， 教授，主要研究方向为无线通信技术；

林志国(1986— )， 博士生，主研信道编解码、调制解调技术研究。

责任编辑：闫雯雯

A Class of QC-LDPC Codes With Girth at Least 10

FAN Wentong1a, MA Linhua1a, LIN Zhiguo1b, ZOU Haoyan2, TIAN Yu3

(1a.AeronauticsandAstronauticsEngineeringCollege;1b.EquipmentManagementandSafetyEngineeringCollege,AFEU,Xi’an710051,China;2.PLAMilitaryRepresentativeOfficeinXi’anAircraftIndustryCorporation,Xi’an710089,China;3.Unit95876ofthePeople’sLiberationArmy,GansuZhangye734100,China)

Aiming at extending the construction methods of quasi-cyclic low-density parity-check (QC-LDPC) codes with good performance and easy applications, a scheme for constructing a class of QC-LDPC codes with girth at least 10 is proposed. First, based on a basis matrix and the 2mcriterion, parity-check matrices with girth at least 10 are constructed. Then, these matrices are transformed with masking matrices. Finally, full rank QC-LDPC codes are obtained. Theory analysis and simulation results show that the construction of these QC-LDPC codes are flexible and they perform very well over the additive white Gaussian noise (AWGN) channel.

communication; girth; full rank; QC-LDPC codes

TN911.22

A

10.16280/j.videoe.2015.19.015

2015-05-24

【本文献信息】范文同，马林华，林志国，等.一类环长至少为10的准循环LDPC码[J].电视技术,2015，39(19).