基于业务区分的频谱接入策略分析

唐 倩，徐家品

(四川大学 电子信息学院，四川 成都 610065)

基于业务区分的频谱接入策略分析

唐 倩，徐家品

(四川大学 电子信息学院，四川 成都 610065)

在认知无线网络中，如何保证认知用户的传输质量，满足其QoS要求是值得关注的问题。首先根据认知用户的QoS要求，将其分成两种等级，实时用户和非实时用户，并分别被建模成M/G/1排队模型，降低了对应的系统时延均值。然后根据系统传输时间均值，讨论了多信道接入策略，通过经典的遗传算法可得最优接入策略，考虑到遗传算法的高复杂度，实际应用中采用反比例接入算法求得次优解，实验数据表明反比例接入算法可以取得与最优接入策略相近的结果且能极大地降低计算时间。

认知无线电；M/G/1排队模型；多信道接入策略；实时性

近年来，随着频谱资源的日渐匮乏，认知无线电技术得到了广泛地关注。美国联邦电信委员会频谱政策任务小组的频谱测量报告显示[1]，大多数的授权频谱资源并未得到充分的利用。在认知无线电中，认知用户可以利用频谱中的空闲频段传输数据，但是当授权用户到来时，认知用户必须退出当前信道，避免对授权用户的传输造成影响，由此，认知用户必须在空闲的频谱空洞之间进行切换，而频繁的切换会造成认知用户通信非常严重的延迟甚至是中断，因此，如何选择合适的信道进行传输，如何有效地进行频谱切换和接入成为衡量认知无线电网络质量的关键技术之一。

目前很多研究都讨论了认知用户频谱利用问题[2-5]。文献[6]建立了基于感知和基于概率两种频谱决策模型解决多个认知用户争夺同一信道，分析相应的系统传输时间，但是其并未考虑共享多个信道的问题。文献[7]讨论了认知用户共享多个信道的问题并建立了多信道虚拟的优先级队列模型，但是在实际的应用场景中，认知网络应该考虑到不同的业务类型和用户，由此可以根据QoS要求将认知用户分级[8-11]。文献[8]中，认知用户数据包被分成实时数据包和非实时数据包，但是这篇文章中只分析了单一信道上认知用户的平均等待时间。在文献[9]中作者将主用户传输系统近似建模为马尔科夫链，讨论了在该马尔科夫信道下不同认知用户业务流的动态频谱接入方案，但是其忽略了认知用户数据包到达和传输的动态性。文献[10]提出了将认知用户分级并分别建模为抢占式的M/G/1排队模型，其有效地降低了实时用户的系统传输时延，然而考虑到遗传算法的高复杂度，在实际应用中可以采用反比例接入算法以降低计算时间。

基于以上讨论，本文将针对认知用户的系统时延分析和多信道的接入策略进行综合分析，并根据认知用户对QoS的要求，将认知用户分为实时用户和非实时用户，提出一种新的接入方案，以期达到有效地降低认知用户的系统传输时延和降低计算复杂度的目的。

1 系统模型及策略描述

1.1 系统建模

图1 引入业务区分的基于概率的频谱决策模型

1.2 频谱接入策略描述

改进的抢占式(Preemptive Resume Priority，PRP)M/G/1排队模型如图2所示。每个信道上构建3个排队队列，其优先级从高到低的排列顺序为PU用户、SU1用户、SU2用户。主用户只能在其对应的授权信道上传输，而认知用户可以根据CR控制中心的频谱决策在M条信道中任意选择一条空闲信道进行传输。如果信道都忙，则新到达的认知用户根据基于概率预测的动态频谱接入策略选择合适的信道并进入相应的队列排队等待。在每条信道上，高等级用户可以抢占低等级用户的传输，只有当高等级队列中的数据包传输完成，低等级队列中的数据包才能进行传输。当高等级用户达到授权信道时，在该信道传输的低等级用户立即中断正在传输的数据包，执行频谱切换，中断的认知用户在原信道上等待，未完成的数据排在相应等级队列的前面。同优先级的用户传输遵从先到先服务原则进入排队序列。

图2 改进的PRP M/G/1排队模型

1.2.1 实时认知用户SU1频谱接入策略

在改进的PRP M/G/1排队模型中，实时认知用户SU1的数据包被等效为次等优先级顾客，由此，SU1用户必须等主用户队列传输完毕才可以进行传输，同时SU1用户可以抢占SU2用户的信道传输数据。SU1用户的频谱接入策略如下：

1)当SU1用户到达时，若系统中还有可用信道，则SU1用户选择主用户数据包到达率最低的信道传输数据，若系统中无可用信道，但是有部分信道被SU2用户占用，则SU1用户抢占主用户数据包到达率最低的信道上的SU2用户进行传输，由此SU1用户的信道接入概率向量P1与信道上主用户数据包到达率成反比。

(1)

(2)

1.2.2 非实时认知用户SU2频谱接入策略

在改进的PRP M/G/1排队模型中，非实时认知用户SU2的数据包被等效为低等优先级顾客，由此，SU2用户必须等主用户队列和SU1用户队列传输完毕才可以进行传输。SU2用户的频谱接入策略如下：

1)当SU2用户到达系统时，若系统中有可用信道，由于SU2用户的数据包传输不仅受主用户影响，还受SU1用户影响，由此SU2用户选择主用户数据包到达率和SU1用户数据到达率最低的信道传输数据。

(3)

(4)

2 系统时延分析

系统传输时间是衡量认知用户QoS的一个重要指标。认知用户的总传输时间(Tsys)包括等待时间(Twait)和有效的传输时间(Ttrans)[5]。认知用户数据包到达系统到开始进行传输这段时间定义为等待时间，认知用户数据包开始进行传输到传输完成的这段时间定义为有效的服务时间。由此认知用户的平均系统传输时间可以表示为

E[Tsys]=E[Twait]+E[Ttrans]

(5)

2.1 实时认知用户SU1的平均系统传输时间

(6)

(7)

由此授权信道k上认知用户SU1的有效传输时间为

(8)

2)SU1用户的排队等待时间。由于认知用户SU1的优先级仅低于主用户，当没有空闲频谱时，SU1用户可以抢占SU2用户的信道进行传输。由此，SU1用户的排队等待时间仅与主用户有关，根据M/G/1排队理论[14]可知

(9)

由此，在共享M个信道时，SU1用户的平均系统传输时间为

(10)

2.2 非实时认知用户SU2的平均系统传输时间

1)SU2用户的有效传输时间。由于SU2用户被赋予了最低优先级，因此在传输的过程中，不仅会被主用户PU抢占信道，还会被SU1用户抢占信道。仿照SU1用户有效传输时间的分析方法，可以得到SU2用户在授权信道k上的有效传输时间表达式为

(11)

2)SU2用户的排队等待时间。由于SU2用户的优先级最低，因此，新到达的SU2用户必须等待该信道上主用户队列、SU1用户队列中的数据包传输完成才能进行传输，此时，假定SU1用户以固定速率到达系统，那么根据M/G/1排队理论[14]可知，SU2用户的排队等待时间为

(12)

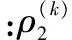
由此，在共享M个信道时，SU2用户的平均系统传输时间为

(13)

3 仿真实现及分析

3.1 时延性能分析

3.2 接入策略优化分析

将分析简化，考虑2个信道的CogWMN系统，假定2个信道具有相同的参数特性：λ0=0.3,λ1=0.1,E[X0]=E[X1]=1。由图5可以得到当2个授权信道上主用户数据包到达率相同时，信道接入概率为P1=P2=(0.5,0.5)，SU1用户和SU2用户的平均系统传输时间均达到最小，E[Tsys1]= 1.455 9，E[Tsys2]=1.554 1。

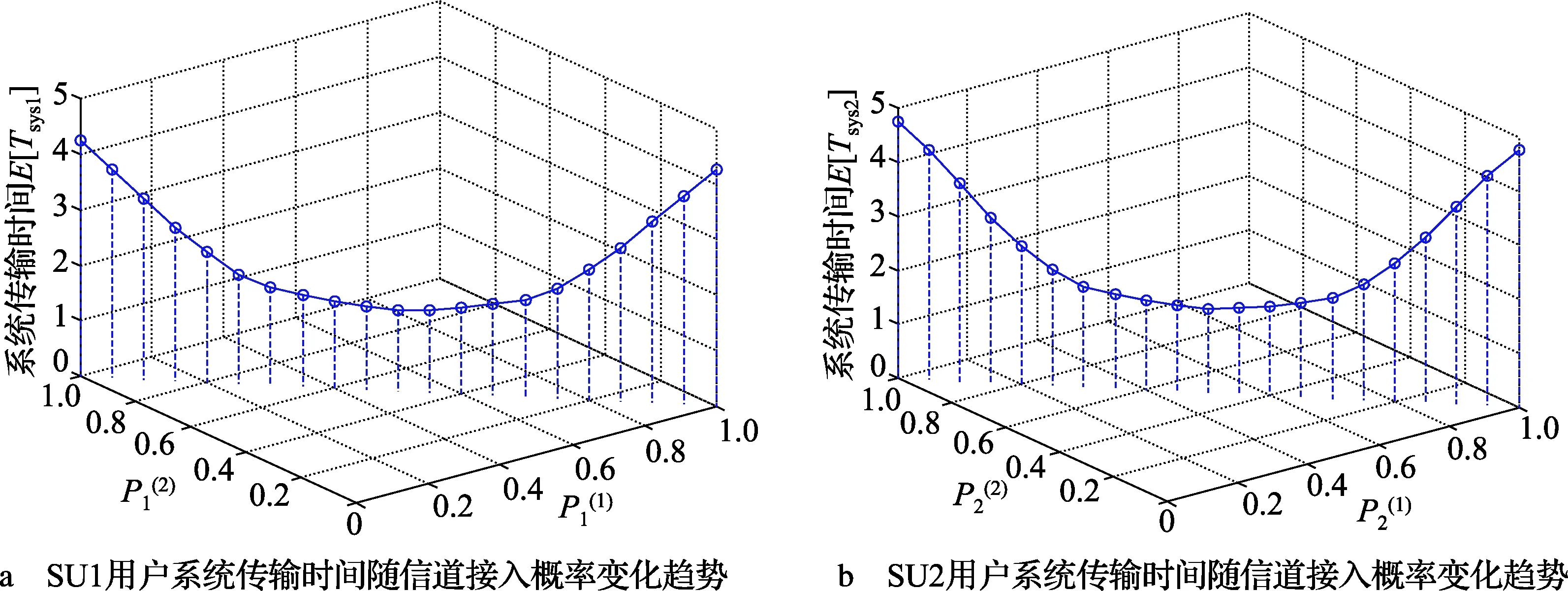
图5 主用户数据包到达率相同时两种认知用户的系统传输时间

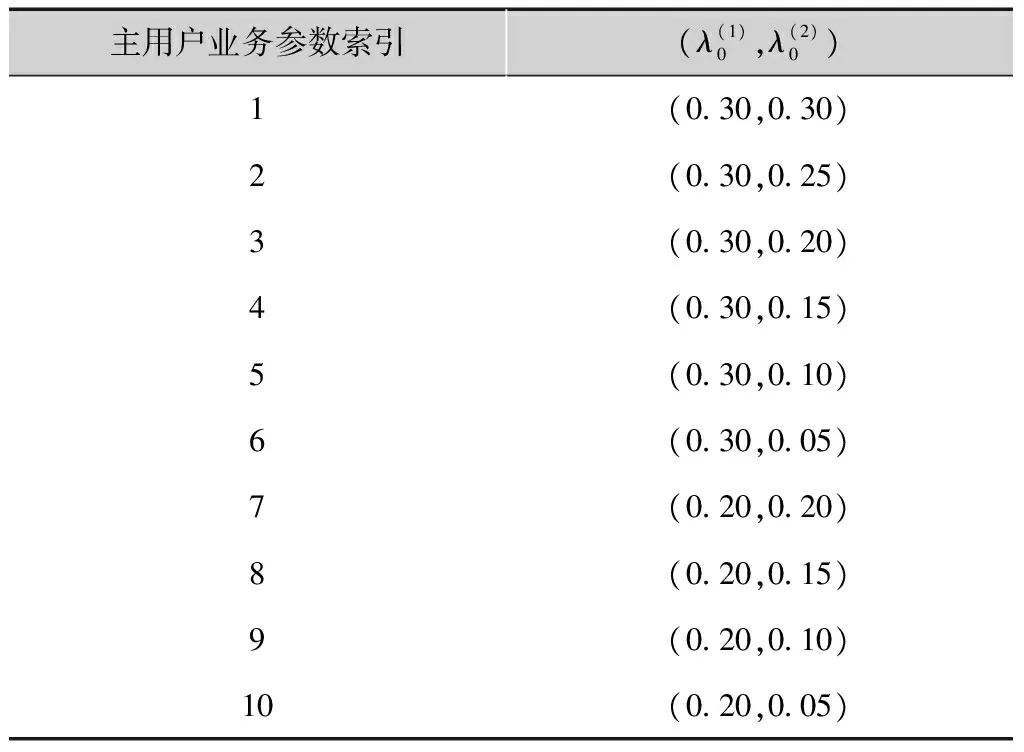
接下来讨论反比例接入算法和遗传算法的比较。不同主用户数据包到达率参数集设置如表1所示，不同策略下2种认知用户平均系统传输时间的比较如图7所示。由图7可以看出，随着主用户业务量的增加，SU1用户和SU2用户的系统传输时间都有所增加，反比例接入策略可以获得与通过遗传算法得到的最优接入策略相近的系统时延均值。通过20次的程序运行时间比较，遗传算法需要进行平均53次迭代得到全程最优解，运行时间长达1.71 s，而反比例接入策略的运行时间仅有1.53 ms，运行时间大大减少，降低了计算复杂度。

图6 主用户数据包不同时两种认知用户的系统传输时间

表1 2个授权信道上主用户数据包到达率参数集

主用户业务参数索引(λ(1)0，λ(2)0)1(030，030)2(030，025)3(030，020)4(030，015)5(030，010)6(030，005)7(020，020)8(020，015)9(020，010)10(020，005)

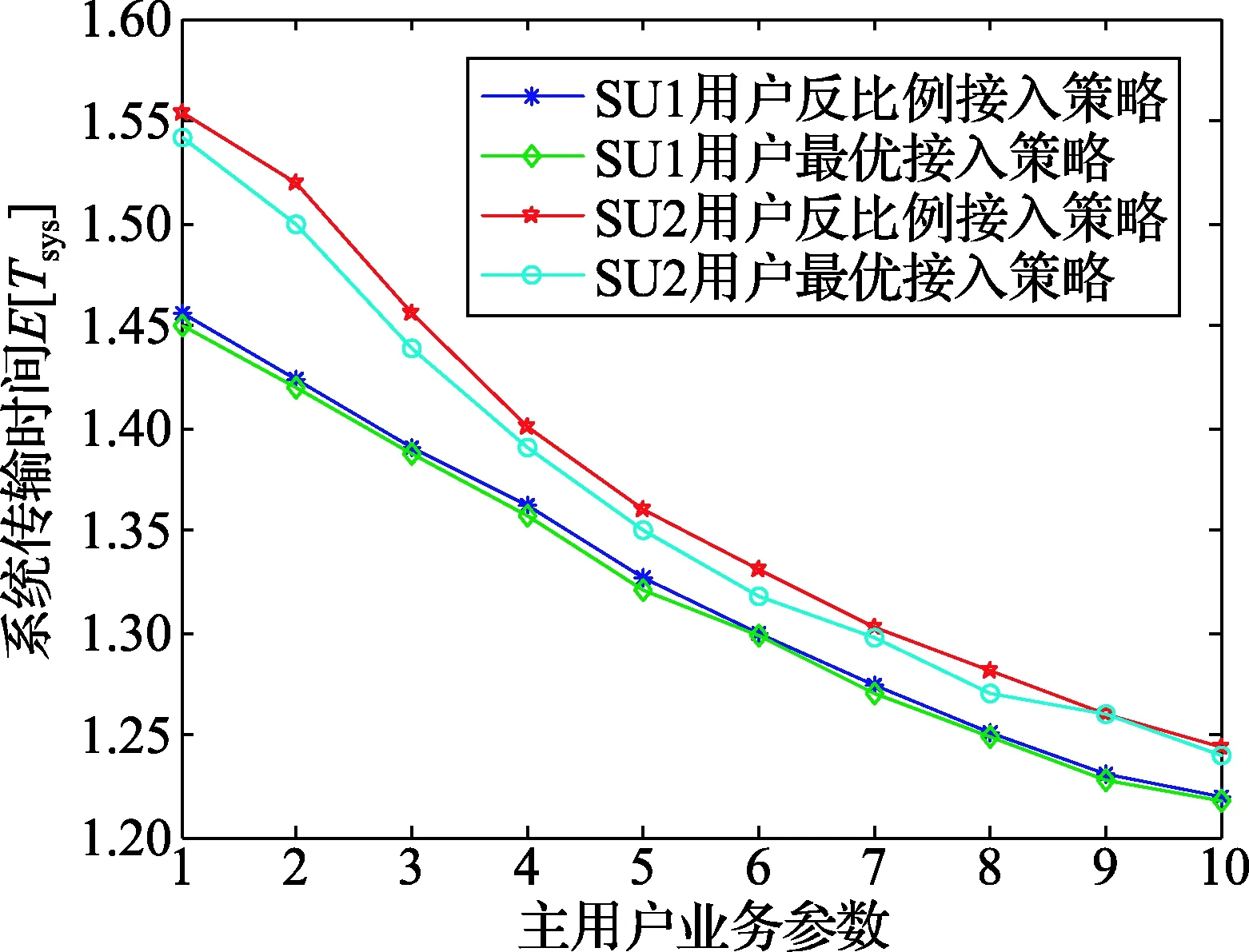
图7 不同接入策略下系统时延均值的比较

4 结论

本文在认知无线网络频谱机会式接入模式下，根据认知用户不同的QoS要求——实时性和非实时性，将认知用户分成两种等级——实时用户和非实时用户。并根据抢占式 M/G/1 排队模型分析了实时用户和非实时用户的系统传输时延。实验结果表明，本文提出的认知用户分级的策略可以在一定程度上降低实时用户的传输时延，能满足实际系统环境中不同QoS要求的用户。基于系统时延的分析，进一步研究了共享多个信道的频谱接入策略，并将其等效为一个非线性问题，通过遗传算法找到认知用户系统时延的最小均值，由此可以求得最佳的多信道接入策略。同时考虑到遗传算法的复杂性，本文采用反比例接入策略求得近似解，这在实际应用中可以节省很大的时间开销。

[1] HOSSAIN E，NIYATO D，HAN Z. Dynamic spectrum access and management in cognitive radio networks[M].London：Cambridge University Press，2009.

[2] ZAHED S，AWAN I，CULLEN A. Analytical modeling for spectrum handoff decision in cognitive radio networks[J].Simulation Modelling Practice and Theory，2013(38)：98-114.

[3] 李文琴，高任. 面向Qos的低复杂度宽带混合频谱接入算法[J].电视技术，2014，38(11)：108-125.

[4] DO C T，TRAN N H，HONG C S. Optimal queueing control in hybrid overlay/underlay spectrum access in cognitive radio networks[C]//Proc. IEEE 75th Vehicular Technology Conference. Yokohama：IEEE Press，2012：1-5.

[5] ZHAO Yuan，JIN Shunfu，YUE Wuyi. A novel spectrum access strategy withα-Retry policy in cognitive radio networks：a queueing-based analysis[J].Journal of Communications and Networks，2014，16(2)：193-201.

[6] WANG C W，WANG L C，ADACHI F. Modeling and analysis of multi-user spectrum selection schemes in cognitive radio networks[C]//Proc. Personal，Indoor and Mobile Radio Communications Symposium. Tokyo：IEEE Press，2009：828-832.

[7] 李潇，王军. 多信道认知无线网络时延性能分析与接入策略设计[J].科学通报，2012，57(21)：2031-2039.

[8] TRAN，DUONG T Q，ZEPERNICK H J. Average waiting time of packets with different priorities in cognitive radio networks[C]//Proc. IEEE 5th International Symposium on Wireless Pervasive Computing. Modena：IEEE Computer Society，2010：122-127.

[9] TUMULURU V K，WANG Ping，NIYATO D. Performance analysis of cognitive radio spectrum access with prioritized traffic[J].IEEE Trans. Vehicular Technology，2012，61(4)：1895-1906.

[10] ZENG Zhen，WANG Gang. Dynamic spectrum access with prioritized secondary users in cognitive radio networks[J].Journal of Information and Computational Science，2013，10(18)：5811-5820.

[11] WU Y Q，HU F，KUMAR S. Spectrum handoffs with mixed-priority queueing model over cognitive radio networks[C]//Proc. 2013 1st IEEE Global Conference on Signal and Information Processing. Austin：IEEE Computer Society，2013：1194-1197.

[12] AKYILDIZ I F，LEE W Y，CHOWDHURY K R. CRAHNs：Cognitive radio ad hoc networks[J].Ad Hoc Networks，2009，7(5)：810-836.

[13] GOLDBERG D E. Genetic algorithms in search，optimization，machine learning[M].[S.l.]：Addison-Wesley Publishing Company，1989.

[14] NG C H，HEE S B. Queueing modelling fundamentals with applications in communication networks[M].USA：Wiley Blackwell，2008.

责任编辑：任健男

Spectrum Access Strategy Design with Prioritized Traffic in Cognitive Radio Networks

TANG Qian, XU Jiapin

(CollegeofElectronicsandInformationEngineering,SichuanUniversity,Chengdu610065,China)

An important issue in cognitive radio networks is the achievable Quality of Service(QoS) performance and high transmission performance for SUs’. Firstly, the SU traffic in the system is classified into two priority classes based on QoS requirements, namely delay-sensitive SU and delay-insensitive SU. The transmission of PU and SUs traffic are modeled as M/G/1 queues, and the overall system time of the prioritized SUs is evaluated based on Preemptive Repeat Priority M/G/1 queueing theory. Then, the access strategy is further investigated with respect to the expected overall system time for SU traffic. The classic Genetic Algorithm(GA) is adopted to minimize the expected overall system time. Considering the complexity of GA, the inverse proportional access strategy is adopted to obtain near-optimal results in practice. The results show that the overall system time by means of the algorithm proposed in this paper is close to that by means of GA and reduces the time.

cognitive radio; M/G/1 queueing theory; spectrum access strategy; delay sensitive

TN92

B

10.16280/j.videoe.2015.19.014

2015-04-17

【本文献信息】唐倩，徐家品.基于业务区分的频谱接入策略分析[J].电视技术,2015，39(19).