基于遗传算法的短波OFDM信道估计导频优化方案

韦世红，孟婷婷，唐 宏

(重庆邮电大学 移动通信技术重庆市重点实验室，重庆 400065)

基于遗传算法的短波OFDM信道估计导频优化方案

韦世红，孟婷婷，唐 宏

(重庆邮电大学 移动通信技术重庆市重点实验室，重庆 400065)

短波信道具有时域稀疏性，压缩感知理论应用于短波OFDM信道估计可以改善估计性能以及减少导频开销。然而信道估计性能和信道的可恢复性都与导频的放置有着密切关系，为了进一步提高信道重构精度，以最小化测量矩阵的互相关为导频优化目标，提出一种基于遗传算法的导频优化方案，并设计了相应的交叉算子和变异算子，以产生新个体，保证种群的多样性。仿真结果表明，相比随机搜索，该方案可以得到更小的互相关值、更高的重构精度以及更高的频带利用率。

压缩感知；OFDM；短波信道估计；导频图案设计；最小互相关；遗传算法

现代短波通信正处于第三代发展后期和启动未来新一代理论与技术研究的重要发展阶段。正交频分复用(Orthogonal Frequency Division Multiplexing，OFDM)是一种特殊的多载波传输方案,其各个子载波相互正交,与一般的多载波系统相比能够节省更多的频谱资源。OFDM技术与短波通信相结合不仅可以适应新一代短波通信“宽带高速”的发展趋势，而且可以有效抵抗短波信道的多径效应及多普勒效应，因而OFDM在短波通信中的应用越来越受到关注。为了有效地进行相干解调，在接收端进行短波信道估计是必不可少的一部分。

由于散射体的空间分布稀疏，短波信道具有稀疏特性[1-2]，传统的信道估计方法不再适用，而基于压缩感知(Compressed Sensing，CS)的稀疏信道估计方法能够有效利用无线信道的固有稀疏性，从而提高信道估计性能[3]。基于导频辅助的信道估计方法一般要在信道估计精度和频谱效率之间权衡，最小二乘(Least Squares，LS)算法采用均匀的导频方式可以获得较好的信道估计性能[4]，然而基于CS的信道重构算法则与此不同。因此，本文旨在研究基于压缩感知的短波信道估计中导频符号的优化设计。

压缩感知理论指出，如果测量矩阵满足受限等距性质(Restricted Isometry Property，RIP)[3],则从理论上可以保证接收端以一定的概率重建信号。然而，目前还没有精确的算法来检查任意给定的测量矩阵是否满足RIP条件，所以RIP准则不适合作为导频优化的准则，这样需要寻找另一种有效的优化准则。文献[5-6]提出测量矩阵互相关值最小准则(Mutual Incoherence Property，MIP)，并指出测量矩阵的互相关值越小，稀疏信号的重构精度越高。信道估计问题也可看作是一种信号的重建，因此以测量矩阵的互相关最小为优化准则，进行导频图案的优化设计。

遗传算法(Genetic Algorithm，GA)是一种高效的全局优化算法，尤其适用于非线性准则[7-8]。其中自然选择过程使得GA可以避免陷入局部最优，并且可以指导算法达到全局最优，得到近似最佳解。因此本文提出基于遗传算法的导频优化方案。

1 系统模型

假设短波OFDM系统中共有N个子载波，其中NP个子载波用来发送导频符号，其位置记为{P1,P2,…,PNP}，其余用来传送数据符号。忽略符号间干扰和载波间干扰，接收信号y=[y1,y2，…，yN]T可以由下式获得

y=FFT(IFFT(X)⊗h+w)=XH+W

(1)

式中：X=diag[x1,x2,…,xN]是一个N×N对角矩阵，表示发送信号；h=[h(0),h(1),…,h(L-1)]T为短波信道的离散时域冲激响应；H为对应的频域响应；当不考虑短波系统内的窄带强单音干扰时,w和W分别代表时域和频域的加性白高斯噪声。

与传统信道估计方法不同，基于CS的信道估计方法通过一定数量的导频和一种CS重构算法可以直接得到稀疏信道的时域冲激响应。短波OFDM信道估计可以看作一种如下的CS问题

yP×1=XP×PFP×LhL×1+WP×1=TP×LhL×1+WP×1

(2)

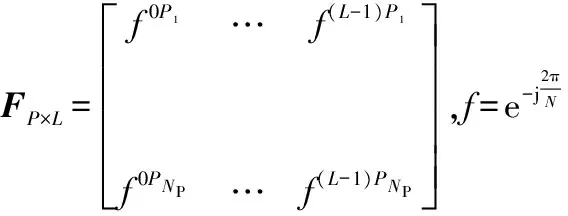
2 导频优化

可恢复性是CS的一个主要研究问题。也就是说一个包含L个元素的未知信号能否从一个所含元素远小于L的观测矢量中恢复出来。压缩感知理论指出如果测量矩阵满足受限等距性质(RIP),则从理论上可以保证接收端以一定的概率重建信号。然而，目前还没有精确的算法来检验任意给定的测量矩阵是否满足RIP条件，所以测量矩阵的互相关最小(MIP)被提出以保证信号的重构。为了得到较高的可恢复性，希望得到互相关最低的测量矩阵。

2.1 问题描述

MIP指出若测量矩阵具有很小的互相关值，则稀疏信号重构质量很高。因此，如果能够得到互相关值较小的测量矩阵，则以此进行短波信道重建的质量较高。

测量矩阵T的互相关μ{T}由以下运算获得

(3)

其中，τi是矩阵T的第i列。将式(2)代入式(3)得

(4)

根据MIP准则，互相关值最小的测量矩阵对应的导频序列argminμ{T}即为希望得到的最佳导频序列。

(5)

这时f(P)只与导频的位置有关。则最优导频序列为：argminf(P)。

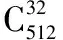
2.2 随机搜索导频优化方案

文献[9]仿真证实了基于CS的信道估计方法，使用随机导频可以获得较好的信道估计性能。为了减少搜索空间，可以在导频放置不规则的集合中搜索互相关值最小的次优解，何雪云[10-11]提出随机搜索导频优化方案，以下称随机优化方案。具体过程描述如下：

1)随机生成M个导频集合，每个集合都含有NP个导频符号；

2)计算每个集合对应的目标函数值f(P)；

3)选择其中最小的目标函数值对应的集合，即最佳的导频方式。

如果M取得足够大，f(P)越小，对应的μ{T}越小，越接近最小的互相关值。

2.3 基于遗传算法的导频优化方案

本文的优化目标是最小化测量矩阵的互相关值μ{T}，所以将1/f(P)作为遗传算法的适应度函数F(x)；这时对适应度产生影响的因素只有导频位置，因此算法中的染色体表示导频的位置。算法的步骤如图1所示。下面对基于遗传算法的导频优化方案进行详细的说明。

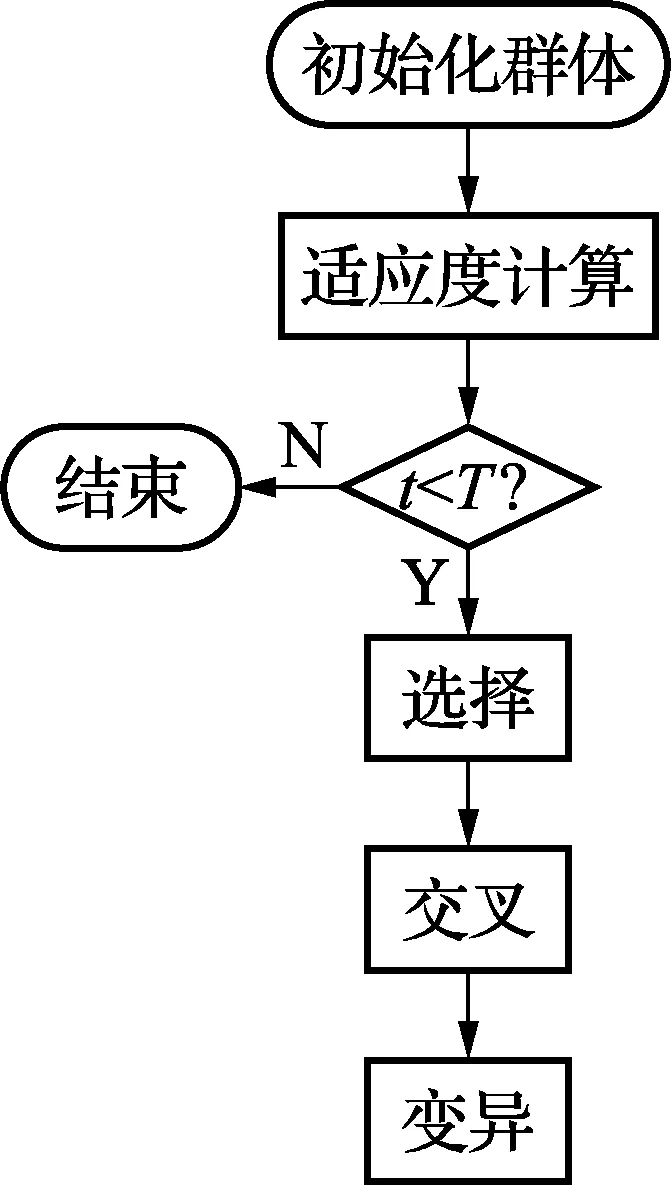
图1 遗传算法流程图

1)编码

基因编码方式对算法的优化性能影响较大，因此需要根据实际问题在导频优化中确定合适的基因编码方式，若采用二进制编码，用来传送导频的子载波表示“1”，传送数据的子载波表示“0”，则二进制编码长度等于子载波数N;若采用实值编码，则只需对导频子载波编码，编码长度仅为NP。考虑到宽带短波OFDM系统中子载波数目N比较大，使用二进制编码占用内存过大，所以本文采用无需解码过程的实值编码。

2)初始化种群

与随机搜索相同，随机产生M个个体(即不同的导频序列)组成一个初始群体，针对这个初始种群进行优化。

3)选择

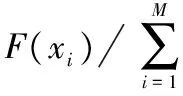
4)交叉

交叉的目的在于产生新的基因组合,以交叉概率从群体中随机选取两个个体配对,并采用适合的交叉算子,产生两个新个体。交叉概率对算法的收敛速度影响较大，如果交叉概率过大则会导致过早收敛。通过实验验证，本文交叉概率应设置在0.2～0.6，具体视种群大小而定。

5)变异

变异模拟了生物进化过程中的基因突变现象,保证了种群的多样性，增加了算法的局部搜索能力。以变异概率随机地从种群中选出个体，再以变异算子产生新个体。变异概率的取值如果太大，导致算法不稳定，如果变异概率超过0.5，算法则退化为随机搜索，所以一般取值为0.001～0.1。

交叉算子和变异算子对交叉和变异过程起着决定性作用，影响着算法的全局搜索能力，而且导频优化问题与经典的TSP、VRP问题不同，导频优化的个体具有随机、不完全遍历的特点，因此在该导频优化方案中设计合适的交叉和变异算子十分必要。

2.3.1 导频优化交叉算子

使用交叉算子进行交叉操作之前，已经对所选择的个体进行了配对操作，本文设计的导频优化交叉算子如下：

1)随机产生一个长度为NP的0-1序列；

2)互换两个体中“1”对应的染色体，“0”对应的染色体不变；

3)如果互换的染色体以外的部分与互换的染色体冲突,用另一父代的相应位置代替，直至没有冲突；

4)将个体中的元素从小到大排序。

2.3.2 导频优化变异算子

导频优化变异算子为：

1)随机选择一个变异点;

2)变异点处的染色体用除自身以外的任意一个1～N的数值代替；

3)如果有冲突，则再从1～N中随机选择一个元素替换，直至没有冲突；

4)将个体中的元素从小到大排序。

3 仿真设计

Rec. ITU-R. F1487(2000)定义了不同纬度、不同环境条件下的2径短波信道。本文仿真中采用其中的“iturHFMD”即中纬度、恶劣条件下的短波信道，并且采用OMP算法完成该短波信道的重构。仿真参数设置如下：信道最大多径时延σmax为2 ms，最大多普勒频移fd为1 Hz,信道带宽24 kHz,信道长度L=50,短波信道稀疏度K=2。OFDM子载波数N=512,采样点数为512,循环前缀长度CP=N/4=128,8PSK调制。遗传算法中的交叉概率为0.3，变异概率为0.05，最大遗传代数T=100。

如图2所示，本次实验随机搜索优化方案中M=100 000，遗传算法优化方案中的初始种群M=1 000。从仿真结果中可以看出，随着导频数NP的增加，互相关值μ逐渐减小，当导频数相同时，遗传优化方案可以比随机优化方案获得更小的μ值，且平均相差0.025；当导频数达到一定数目(32个)后，μ值的下降幅度变得平缓，继续增加导频反而会降低系统的频带利用率。考虑此因素，在接下来的短波信道估计中，OMP算法采用32个导频进行短波信道的重建，其BER性能如图3所示。

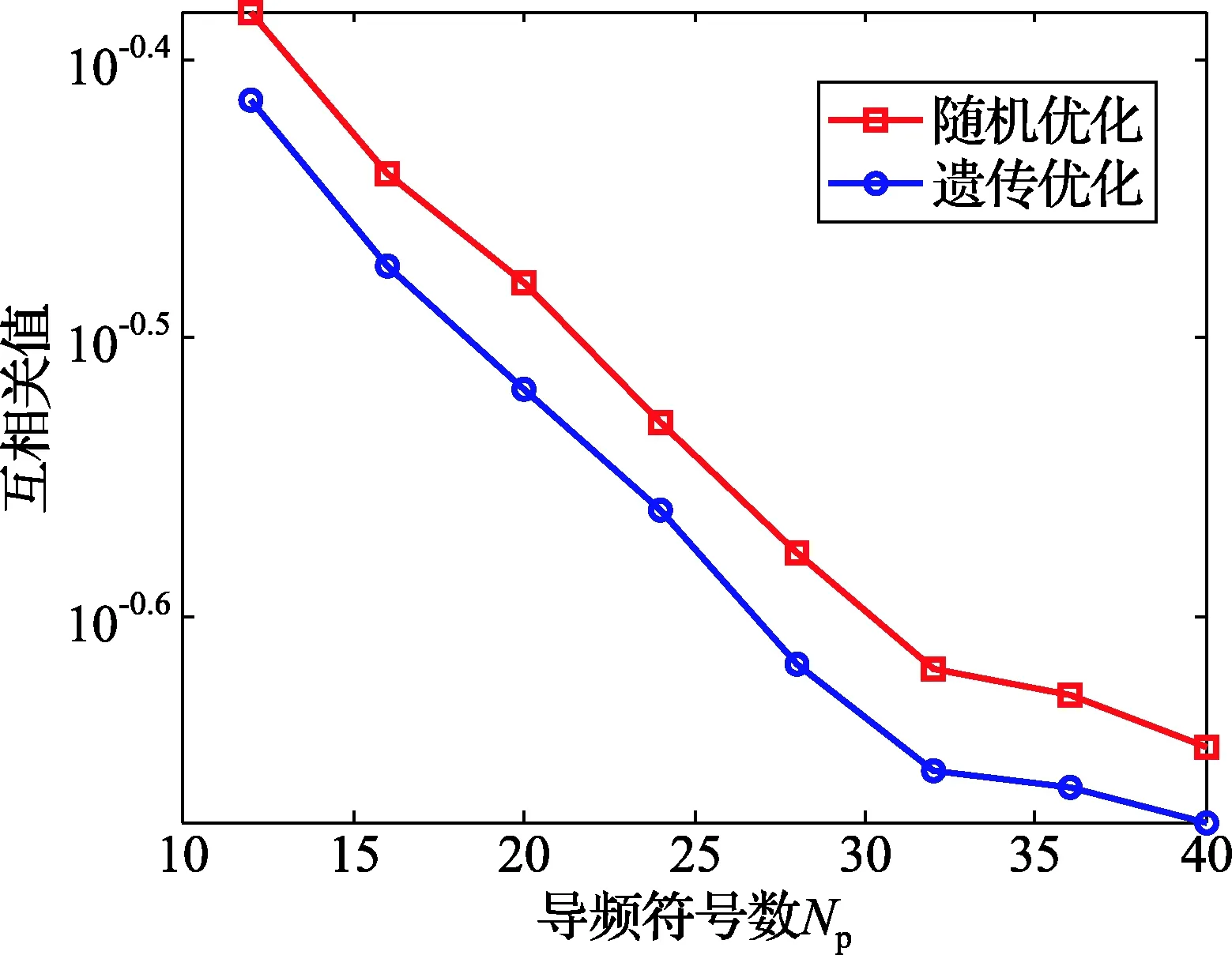
图2 导频数对互相关值的影响

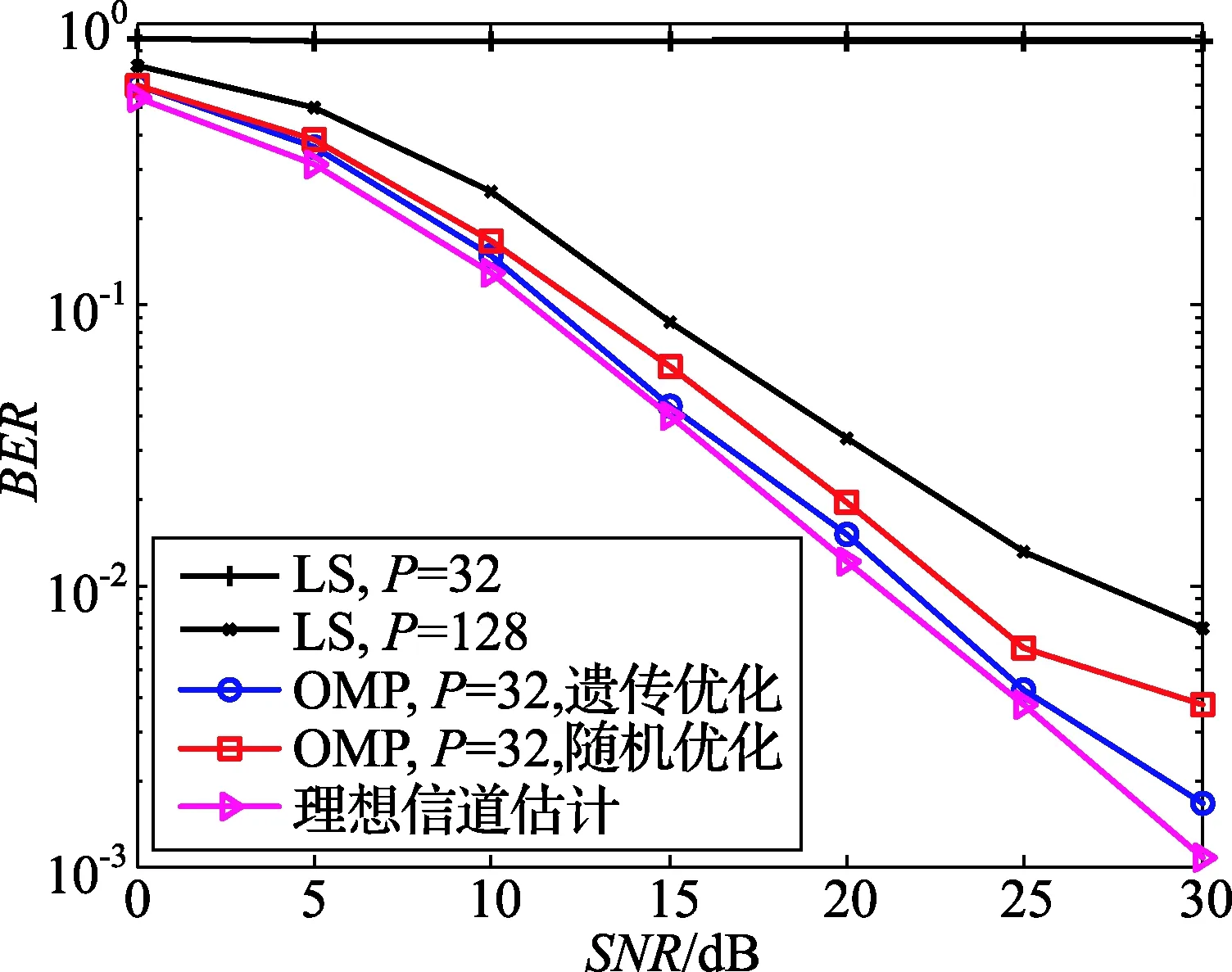
图3 BER性能比较

图3中，为了突出对比，传统信道估计算法LS采用性能最佳的均匀导频，并设置导频数分别为32和128；OMP算法仅使用32个导频，导频结构分别由随机优化和遗传优化得到；理想信道估计是指接收端在已知信道的冲激响应的情况下得到的信道估计值。

对比LS和OMP算法的BER曲线，当NP=32时，LS不能有效进行短波信道估计，而OMP则可以将BER控制在10-2以下，能够较精确地得到信道信息；虽然当NP=128时，LS可以精确地估计信道，但是相比OMP，LS算法牺牲了18.75%的系统频带。这也证明了压缩信道估计方法在保证较高的信道估计性能的条件下，可以比传统信道估计方法节省大量导频，提高系统频带利用率的结论。对比采用两种导频优化方案的OMP算法的BER曲线，在信噪比固定时，采用遗传优化方案的BER要比采用随机优化方案的BER平均降低 0.011 8， 并且前者的BER性能已经接近理想信道估计的BER性能。这一对比再次证明了本文提出的遗传优化方案的有效性。

为了保证较高的信道重构精度，μ值应取值较小，所以本次仿真了μ值在0.2～0.3之间时两种优化算法的运行时间，仿真中μ值精确到小数点后两位(见图4)。从图中可以看出，达到同一μ值时，遗传优化方案要比随机优化方案耗费 3～4 倍的时间，但是要比随机优化方案节省2%左右的导频。如μ=0.233 1，遗传优化方案中需32个导频，其导频序列为 {38， 51，77，85，101，137，179，183，205，214，245，264，268，271，276，284，296，313，320，330，347，378，385，423，428，442，451，456，466，471，474，496}；μ=0.234 7，随机搜索导频优化方案需36个导频，其导频序列为{ 3，9，18，37，47，56，72，90，97，99，105，116，133，157，163，169，178，245，247，252，307，314，320，324，332，348，363，366，393，416，429，431，451，472，487，504}。考虑到实际短波的频谱资源短缺，牺牲一定的运行时间来换取频谱利用率的提高也是值得的。再者，为了解决导频优化步骤产生的接收两端的延时问题，可以事先通过基于遗传算法的导频优化方案获得多组不同情形下的导频集合，构成一张导频序列表，储存在收发设备中供双方协商使用，不会影响系统的实时性。

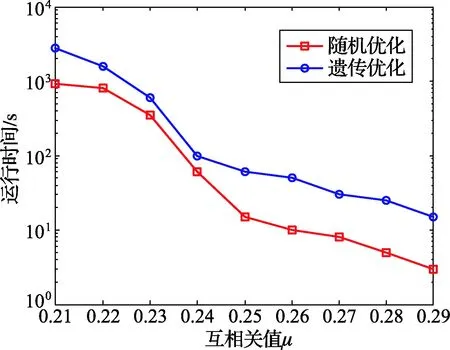
图4 运行时间对比

4 结论

针对基于CS的短波信道估计，以最小化测量矩阵的互相关为优化目标，提出一种基于遗传算法的导频优化方案，并提供了符合导频优化操作的交叉算子和变异算子，从而产生新的个体，保证种群的多样性。仿真实验结果验证了本文工作的有效性，相比传统LS算法，基于CS的短波信道估计方法不但改善了估计性能，而且节省了导频开销，提高了18.75%的频带利用率；使用导频数相同时，本文提出的遗传优化方案可以比随机优化方案获得更小的互相关值，并且在信噪比相同的情况下，遗传优化方案的误码率要比随机优化方案的误码率平均降低0.011 8；互相关值相同时，遗传优化方案要比随机优化方案费时，但是导频图案的优化是在系统设计阶段完成的，不会增加实时系统的时延，另一方面，考虑遗传优化方案可以节省若干导频，所以更适合短波OFDM系统的导频优化。

[1] BERGER C R, WANG Z H , HUANG J Z, et al. Application of compressive sensing to sparse channel estimation[J]. IEEE Communications Magazine, 2010, 48(11)：164-174.

[2] 应军科. 基于压缩感知的宽带短波OFDM信道估计[D].杭州：浙江大学，2013.

[3] XIE H, ANDRIEUX G, WANG Y D, et al. A novel effective compressed sensing based sparse channel estimation in OFDM system [C]//Proc. 2013 IEEE International Conference on Signal Processing, Communication and Computing (ICSPCC). Kunming：IEEE Press，2013：1-6.

[4] BARHUMI I，LEUS G，MOONEN M. Optimal training design for MIMO OFDM systems in mobile wireless channels [J]. IEEE Trans. Signal Process，2003，51(6)：1615-1624.

[5] DONOHOD L, ELAD M, TEMLYAKOV V. Stable recovery of sparse over complete representations in the presence of noise[J]. IEEE Trans. Information Theory，2006，52(1)：6-18.

[6] MANASSEH E，OHNO S，NAKAMOTO M. Pilot symbol assisted channel estimation for OFDM-based cognitive radio systems[J]. Journal on Advances in Signal Processing，2013，51(1)：1-11.

[7] GUO P F, WANG X Z，HAN Y S. The enhanced genetic algorithms for the optimization design[C]//Proc. 2010 3rd International Conference on Biomedical Engineering and Informatics (BMEI). YanTai：IEEE Press，2010：2990-2994.

[8] SILVEIRA L R，TANSCHEIT R，VELLASCO M. Quantum-inspired genetic algorithms applied to ordering combinatorial optimization problems [C]//Proc. 2012 IEEE Congress on Evolutionary Computation (CEC). Brisbane，QLD：IEEE Press，2012：1-7.

[9] 何雪云，宋荣方，周可琴. 基于压缩感知的OFDM系统稀疏信道估计新方法研究[J].南京邮电大学学报：自然科学版，2010，30(2)：60-65.

[10] 何雪云，宋荣方，周克琴. 认知无线电 NC-OFDM 系统中基于压缩感知的信道估计新方法[J]. 通信学报，2011，32(11)：85-94.

[11] 何雪云，宋荣方，周克琴.基于压缩感知的OFDM稀疏信道估计导频图案设计[J].南京邮电大学学报：自然科学版，2011， 31(5)： 7-11.

孟婷婷(1990— )，女，硕士生，主研移动通信理论与技术；

唐 宏(1967— )，教授，博士，主要从事移动通信与计算机网络等方面的科研与教学工作。

责任编辑：许 盈

Genetic Algorithms Based Optimization Scheme of Pilot Pattern for HF Channel Estimation in OFDM System

WEI Shihong, MENG Tingting, TANG Hong

(ChongqingKeyLabofMobileCommunicationsTechnology,ChongqingUniversityofPostsandTelecommunications,Chongqing400065,China)

Short wave (HF) channel is a kind of time domain sparse channels, the application of the recent theory of compressed sensing has proved its efficiency to both ameliorate the estimation accuracy and reduce the transmitted overhead. The performance and uniqueness guarantee of recovery remain however closely related to the pilots placement. In order to further enhance the performance of the estimation, the deterministic design of pilot pattern is investigated based on minimizing the coherence of the measurement matrix， then a pilot design scheme is proposed based on genetic algorithms， and a suitable crossover operator and mutation operator are designed to generate new individuals. Simulation results show that compared with the random search, the proposed scheme can get a smaller cross-correlation value, higher reconstruction accuracy and higher spectral efficiency.

compressed sensing; OFDM; HF channel estimation; pilot pattern design; cross-correlation minimization; genetic algorithms

国家留学基金项目(201407845013)；应急通信重庆市重点实验室开放课题；重庆市科委重点实验室专项；重庆邮电大学自然科学基金项目(A2011-51)

TN929.5

A

10.16280/j.videoe.2015.19.012

韦世红(1970— )，女，副教授，硕士，主要研究方向为下一代网络和智能光网络技术；

2015-06-10

【本文献信息】韦世红，孟婷婷，唐宏.基于遗传算法的短波OFDM信道估计导频优化方案[J].电视技术,2015，39(19).