采用生产数据的给煤计量聚类组合算法

钱 虹，郜建良，陈 纲，周 泉

(1.上海电力学院 自动化工程学院，上海 200090；2.上海市电站自动化技术重点实验室,上海 200072；3.华能 上海石洞口第一电厂，上海 200942)



采用生产数据的给煤计量聚类组合算法

钱 虹1,2，郜建良1，陈 纲3，周 泉3

(1.上海电力学院 自动化工程学院，上海 200090；2.上海市电站自动化技术重点实验室,上海 200072；3.华能 上海石洞口第一电厂，上海 200942)

为了降低锅炉运行能耗，充分发挥锅炉运行的效率，支撑节能减耗，需要对给煤量进行准确的测量。本文通过引入转速比给煤率，作为给煤量计量的标准，采用灰色聚类小波去噪组合算法，对实际生产数据进行处理，得出转速比给煤率比值的大小。通过采用此方法对某电厂数据进行分析，证明了方法可行，具有推广意义。

给煤量；皮带秤；灰色聚类分析；小波去噪

0 引言

随着市场经济的发展，在厂网分开后，电力市场实施了竞价上网的市场机制。火电厂为了降低成本、提高效益，燃煤量的计量就成为了其生产经营中不可缺少的一项重要工作[1]。在火电厂燃煤量计量的众多方法中，运用皮带秤来计量燃煤量应用较为广泛。但在实际的运行中，由于皮带张力、环境、温度及湿度、托辊轴承摩擦力等诸多外在因素的影响[2-4]，经常导致皮带秤的测量不准确，偏离正常值。因此，当发现皮带秤测量不准确时，采取一定的手段对皮带秤给煤计量进行校核是非常必要的。目前电厂缺乏对给煤量计量的校核手段。本文引入转速比给煤率，见式(1)，当式中d、△和n这3个值确定时，k只与单位长度皮带上煤质量c有关，而c与煤的密度有关。在一段时间内，由于煤质相近，所以煤密度c可以用一个常数表示。因此，在这段时间内转速比给煤率k为一个常数。此常数可以作为给煤计量校核的标准，但此常数较难获取。本文采用数据分析的方法得到此比值。

(1)

式中：k为转速比给煤率；c为单位长度皮带上煤质量；d为驱动轮直径；△为皮带厚度；n为皮带减速器减速比。

从大量数据中获取有效数据的方法有很多，聚类分析法就是其中的一种[5]，目前，在样本获取中的应用有水电站水位的估算[6]、水果加工品质评价[7]等。由于在数据的采集过程中存在电磁干扰，所以对采集到的数据需要进行去噪，小波去噪算法就是众多去噪方法中的一种，目前在数据处理中的应用有：焊接缺陷信号的处理[8]、纳通道内DNA过孔信号的提取[9]等。本文主要应用灰色聚类小波去噪组合算法，首先，运用灰色聚类对数据进行处理，得到转速比给煤率的有效数据和正常范围。然后，运用小波去噪对通过聚类获得的有效数据进行处理，得到去噪后的有效数据。最后，对去噪后的有效数据求期望值，此期望值就反映了当前皮带秤的测量水平。通过运用生产数据进行验证，结果准确，证明了此方法的可行性和有效性。

1 灰色聚类小波去噪计量算法

本文所应用的算法是基于灰色聚类算法和小波去噪算法的组合算法。首先，运用灰色聚类法对原始数据进行聚类分析，得到有效数据，然后运用小波去噪对有效数据进行去噪，得到去噪后的有效数据。

图1 灰色聚类和小波去噪组合算法结构图

算法结构见图1。

1.1 灰色聚类法提取有效样本

聚类分析是对样本或指标进行分类的一种多元统计分析方法，其目的是在事物类别未知的情况下，把研究的对象按照一定的规则分成若干类，使各个类内的对象尽可能具有最大的相似性,不同类之间的对象尽可能有最大的相异性。灰色聚类分析是众多聚类方法中的一种，本文主要运用灰色星座聚类法，其基本原理为：将每个样本点按一定的数量关系，点在一个上半圆之中，一个样点用一颗“星点”来表示，同类的样点便组成一个“星座”，然后勾画出不同星座的界线，这样就可以进行分类。此方法遵循的聚类准则为类内方差准则[10]。分析步骤如下：

首先，对原始数据指标值进行极差变换，使变换后的数值均落在[0°，180°]的闭区间内，如式(2)：

(2)

式中：aij为变换后以角度表示；xij为原始数据；xjmax为第j个变量的最大值；xjmin为第j个变量的最小值。

然后，对每个指标，根据其对系统变化的影响程度，分别给一个权数wj，使

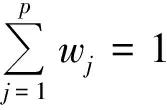
(3)

式中：wj为第j个指标的权数。

利用极坐标与直角坐标的变换关系，先求出每一点各项指标的Xi、Yi值，然后将各点每项指标Xi、Yi值相加，即为各样点的坐标值，其变换公式为：

(4)

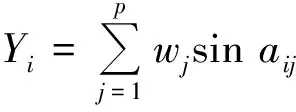
(5)

式中：Xi为第i样点的横坐标；Yi为第i样点的纵坐标。

绘制一个半径为1的上半圆，以圆中心为坐标原点，以上半圆底为横坐标X轴，并作出过原点的Y轴，根据Xi、Yi的值确定每一个样点在星座园内的位置，将性质接近的点聚在一起，形成一个“星座”。

最后，求取综合指标值，如式(6)。根据综合指标值以及星座图的聚类情况，确定分类结果。通过综合指标值反推出各个类的边界值。

(6)

式中：zi为综合指标值。

在聚类结束之后，运用类内方差对聚类结果进行验证，σ较小时证明聚类结果合理；反之，聚类结果不合理，需重新进行聚类。本文根据数据分析取0.3作为判断σ的标准。公式如下：

(7)

式中：σ为类内方差；wj为第j个指标权数；xij为第j个指标的第i个数据；xjT为第j个指标的期望值。

1.2 小波算法进行去噪滤波

小波变换采用改变时间-频率窗口形状的方法，很好地解决了时间分辨率和频率分辨率的矛盾，在时间域和频率域里都具有很好的局部化性质。对信号中的低频成分，采用宽的时间窗，得到高的频率分辨率；对信号中的高频成分，采用窄的时间窗，得到低的频率分辨率[11-12]。

设函数ψ(t)∈L2(R)，满足条件∫Rψ(t)dt=0，其中ψ(t)为基本小波。

将基本小波进行伸缩和平移，得到下列函数族：

(8)

(9)

通常取∫R|ψ|2dt=1，其意义是ψ(t)具有单位能量。

函数f(t)∈L2(R)的连续小波变换CWT定义为：

(10)

设一个含有噪声的信号模型描述为：

S(x)=f(x)+n(x)，

(11)

式中：S(x)为降质信号；f(x)为原信号；n(x)为噪声信号。

由于小波变换是线性变换，所以降质信号的小波系数是信号的小波系数和噪声的小波系数之和，降质信号的离散逼近部分和离散细节部分，分别是信号变换后的离散逼近部分和离散细节部分与噪声变换后的离散逼近部分和离散细节部分的和。因此，在消噪过程中，利用信号与噪声在小波变换后，各自的小波系数的性质不同，可以消除或减弱噪声。

2 在火电厂燃煤量计量中的应用

本文的数据处理是基于Matlab运算环境。首先，对在某电厂获得的7月1日至7月15日的转速和给煤率近1万条数据进行处理(采样时间间隔为1 min)，得到转速比给煤率的值。如式(12)，式中n与时间有关，n为9 871。

[x1,x2,x3,x4，…,xn]=[20.865 509,21.258 846,21.686 264,21.429 733,21.298 002,21.399 473, 21.995 590,21.547 398,21.044 653,20.865 509,21.044 653,21.495 592, 21.134 037,20.922 691,21.260 214,20.916 540,21.233 000,21.092 566, 21.359 013,20.944 597,21.228 924,21.175 158,21.383 318,21.063 284, 21.133 812,21.142 336,21.097 799,21.232 336,20.971 466,20.857 504, 21.100 887,21.000 240,20.888 977,21.045 385,20.944 305,20.992 451,…, 21.081 293,21.186 115,21.200 815,21.061 571]。

(12)

对得到的转速比给煤率的值进行聚类处理，利用极坐标与直角坐标的关系，求出每个样本点对应的横坐标值和纵坐标值。在进行计算时权值w取1。将得到的坐标绘制聚类星座图，如图2所示。

分别求取各个样本的综合指标值，并对综合指标值进行作图，如图3所示。由图3可以发现：综合指标值绝大多数落在2.876 5～2.877 5。

通过星座图和综合指标值的综合分析可以得出：转速比给煤率有效范围为19.5～22.5，类内方差为0.185 4。通过对半个月的转速比给煤量近1万个数据统计发现，按照类内方差为0.185 4进行划分，不在此范围内的样点一共有67个，因此，在此范围内的数据可以反映转速比给煤量的数据特性，具有统计意义。

图2 聚类星座图图3 综合指标

对在上述范围内的转速比给煤率进行小波去噪，本文选用db3作为基本小波，并进行3级去噪。去噪前后的图像如图4a和图4b所示。由图4可以看出：去噪后的信号很好地保留了原有的趋势特征。最后，对去噪后的数据进行求期望值，结果为20.960。此期望值可以反映本台给煤机在这一段时间内的皮带秤的测量水平，运行人员可以根据这个值对皮带秤进行校核。

图4 转速比给煤率(7月1日至7月15日)

下面运用8月3日至8月17日的转速和给煤率数据对上述求取的范围进行验证。通过处理发现：在1万个数据中，只有17个不在范围内，类内方差为0.042 7，有99.79%的数据在此范围内，证明了范围的有效性和通用性。然后，对范围内的数据进行去噪处理，去噪前后的图像如图5a和图5b所示。对去噪后的数据求期望值，结果为20.762。

图5 转速比给煤率(8月3日至8月17日)

3 结论

(1)通过引入转速比给煤率，为运行人员提供了判断皮带秤测量准确性的依据，同时提高了燃煤量计量的准确性。

(2)由于在数据采集过程中存在干扰，引起数据测量的不准确，本文通过灰色聚类法的有效处理，很好地解决了这一问题，提取了有效样本。

(3)在应用灰色聚类的基础上，运用小波去噪算法对得到的有效数据进行去噪处理，对去噪后的数据进行求期望值，此期望值可以反映皮带秤在一段时间内测量水平，运行人员可以通过此期望值来判断皮带秤测量的准确性。

本次针对半个月的数据进行处理，随着运行时间的增长、数据量的增大，得到的转速比给煤率合理波动范围将更加准确。

[1] 张勇胜,闫慧博,赵晓光,等.锅炉净效率简化算法在火电厂节能技术监督中的应用[J].河北电力技术,2012,31(3):28-29.

[2] 谢光辉.电子皮带秤计量误差的动态分析[J].计量与测试技术,2010,37(4):31-32.

[3] 严荣涛,王玉玺.火电厂皮带秤入炉煤计量一个特殊典例[J].衡器,2014,43(1):39-42.

[4] 周亚全,况金宏,蒋庆辉.提高电子皮带秤计量准确度的有效方法[J].自动化仪表,2013,34(1):92-94.

[5] 王祥斌,杨柳,邓伦治.一种利用高斯函数的聚类算法[J].河南科技大学学报:自然科学版,2014,35(5):33-36.

[6] 李辉,申建建,廖胜利,等.基于模糊聚类分析的水电站日初水位估算[J].中国电机工程学报,2010,30(35):118-123.

[7] 公丽艳,孟宪军,刘乃侨,等.基于主成分与聚类分析的苹果加工品质评价[J].农业工程学报,2014,30(13):276-285.

[8] 王玉,高大路,廖明夫,等.焊接缺陷信号的小波去噪方法研究[J].西北工业大学学报,2005,23(4):496-499.

[9] 王霏,倪中华,陈云飞,等.纳通道内λ_DNA过孔信号的小波去噪及统计分析[J].东北大学学报:自然科学版,2013,43(1):50-54.

[10] 罗会兰.聚类集成理论与其在图像分类中的应用[M].北京:科技出版社,2012.

[11] 方利民,林敏.小波聚类方法和近红外光谱技术用于药片种类判别[J].光谱学与光谱分析,2010,30(11):2958-2961.

[12] 葛耀峥,林泽涛,陶国良.心电信号在线数据知识化辅助诊断算法研究[J].浙江大学学报:工学版,2006,40(2):238-242.

上海市重点实验室基金项目(04DZ05901)

钱 虹(1967-),女,上海人,副教授,博士,主要研究方向为控制理论方法与应用.

2015-02-08

1672-6871(2015)04-0051-05

TM621

A