冰区航行船舶阻力预报方法
郭春雨,李夏炎,谢畅,赵大刚
(哈尔滨工程大学船舶工程学院,黑龙江哈尔滨150001)
近年来,随着全球气候变暖、冰川融化现象加剧,极地科考和开发工作越来越受到相关国家的重视。破冰船、冰区加强船、科考船等冰区航行船舶性能研究工作已经迫在眉睫。目前,我国对于冰区航行船舶的研究,尤其是船舶性能的研究尚处在起步阶段。
在冰区航行船舶性能研究中,阻力预报一直是一个重要而复杂的问题。1964年,Corlett等[1]以石蜡代替冰,第一次完成了冰区船阻力模型试验,之后,通常采用基于模型试验的经验公式方法预报冰区船阻力。近年来,数值模拟算法日益成熟、计算能力提高,在冰区船阻力预报领域的应用也受到了更多人的关注。目前,冰区船阻力预报问题没有一个普遍的准确方法,经验公式方法、数值模拟方法和船模试验方法虽然都能在一定程度上对冰区船舶航行阻力进行预报,但也具有各自的局限性。
1 经验公式预报方法
经验公式预报方法是一种基于模型或实船的大量试验结果的数学公式计算预报方法。该方法的阻力方程并不立足于物理定律和理论分析,而是一种部分计及误差概率的数学公式,通过数学方法求出系数和幂的量值,并加以修正[2],最终得到冰阻力预报公式的一般形式和公式中的无量纲系数。
大多数经验公式根据物理背景的不同,把冰阻力划分成几个独立的部分。1956年,Jansson[3]讨论了冰区船阻力的影响因素,简单地将阻力分为与速度相关的部分和与速度无关的部分。之后,也有研究者进一步的根据阻力来源的不同对其进行细分,Kashteljan等[4]将冰阻力划分为破冰力、碎冰翻转力、碎冰滑动力和水阻力4个部分。
1975 年,Vance[5]开发了一套基于船长和船宽的最优回归方程用于预报破冰船航行阻力,该方程与5组实船和船模试验数据吻合得很好。至今,根据不同海域、不同级别的冰区船实船/模型试验数据得到的阻力预报经验公式层出不穷[6-10],它们都是由对应船型的试验数据得到的,一个确定系数的经验公式只能对一种船型使用。
1.1 Spencer算法
1992 年,Spencer[11]将总船舶阻力分为 4 个部分:RT=Row+RB+RC+RBR(式中:RT为总阻力;Row为敞水阻力;RB为冰浮力阻力 ;RC为冰清除阻力;RBR为破冰阻力)。2001年,Spencer等[10]成功将该公式应用在模型和实船计算中,并在后来根据加拿大R级破冰船的试验数据来确定冰阻力计算公式中的无量纲系数。2009 年,Seong-Yeob Jeong[12]应用模型试验对该理论进行了验证和进一步研究。通过对不同类型和尺寸的破冰船推广使用Spencer的冰阻力预算公式,结合已公布的船模、实船试验,能够获得对应船型的无量纲系数。
最终得到的冰阻力通用计算公式为


1.2 Lindqvist算法
1989 年,Gustav Lindqvist[8]提出一种计算冰阻力的方法,将总阻力分为破冰阻力、水下阻力和与速度相关的阻力3个部分(其中破冰阻力分为船艉挤压力和弯曲破坏力2个部分)。
1.2.1 破冰阻力
测量船艉挤压力是比较困难的,可以用概率的方法近似估算,作用在冰上垂直分量的力FV估算为

式中:σf为冰的弯曲强度,hi为冰厚。
通过分析挤压过程和对几何方面的考虑可以得出挤压阻力RC为

弯曲破坏力RB可以表示为


式中:hice为冰厚,E为杨氏模量,ν为泊松比,σf为冰弯曲强度,B为船宽,g为重力加速度,ρw为海水密度。
1.2.2 水下阻力
水下阻力RS由2个部分组成:潜在的能量损失和摩擦阻力,阻力值可由公式计算:

式中:ρi为冰密度,ρw为水密度,T为最大吃水,L为船长,htot为冰和雪的总厚度。
1.2.3 速度有关的阻力
与速度相关的阻力与其他部分相比具有更不确定性。从研究来看,这部分阻力随速度的增加呈线性增加。
综合以上4个部分,用经验常数获得总的冰中航行阻力可以表示为
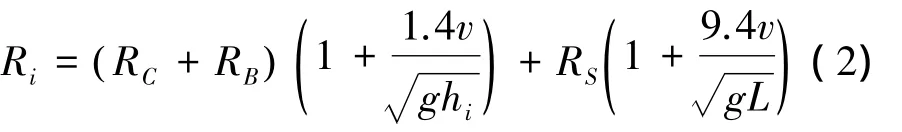
1.3 Riska 算法
Riska[9]的阻力计算公式也是建立在一系列经验系数基础之上的公式,其中的经验系数都是从波罗的海的不同船型的多组实船试验得到的。
Riska阻力的主要表达公式为RT=Ropenwater+Rice,即将冰中的航行阻力分为独立的2个部分:敞水阻力Ropenwater和冰引起的阻力Rice。目前船舶敞水阻力的预报方法比较成熟,而对于冰中的阻力Ri,分为与速度相关的惯性阻力和与速度无关的直接阻力2个部分,表达公式为

其中:

式中:L、B、T分别表示船的长度,宽度和吃水,V为船体速度,φ为艏倾角,hi为冰厚,Lpar和Lbow分别是平行中体的长度和船艏长度。公式中的经验系数f、g 的取值见表 1[9]。

表1 Riska公式中的系数Table 1 Coefficients of Riska’s formula
1.4 Enkvist算法
Enkvist[7]通过对 3 艘破冰船(“Moskva-class”号、“Finncarrier”号和“Jelppari”号)的模型试验结果与实船资料进行比较,结合物理分析、无量纲化处理以及假设简化,推导出了基于以下3项的冰阻力半经验公式:
RTOT=C1Bhσ +C2BhTρΔg+C3Bhρiv2(6)式中:RTOT为冰阻力,B、T分别表示船的宽度和吃水,h为冰厚度,σ为冰弯曲强度,ρi为冰密度,ρΔ为水与冰的密度差,g为重力加速度,v为船速,C1、C2、C3为无量纲系数。在试验中,通过在低速(v≈0)和正常航速下进行对比,能够隔离速度相关项;通过进行预切割冰(σ=0)试验,能够隔离下沉项。这种试验设计方法能够确定方程中3项阻力成分的相对重要性。
1.5 芬兰瑞典规范推荐算法
芬兰瑞典规范中提供了船舶在碎冰中航行受到阻力的计算公式[13]:

式中:μB=1-p,p为孔隙率(μB=0.8~ 0.9),ρΔ为冰和水密度的差值,g为重力加速度,Kp为钝化应力(土力学),δ为碎冰侧壁的倾角,μh为冰和船体之间的摩擦系数,L、B、T分别表示船的长度,宽度和吃水,φ为水线与中纵剖线间的夹角,ψ为外飘角,α为水线入射角,K0为静止侧压力系数,Lpar为水线处平行中体的长度,AWF为船体艏部水线面面积,Fn为傅汝德数。HM为航道正中间碎冰的厚度,HF表示从船艏移动到平行中体两侧的碎冰层的厚度,它是一个关于船宽、航道厚度和2个取决于碎冰的内部性质的倾斜角度γ和δ的函数(通常取γ=2°,δ=22.6°),如下所示:

当B﹥10 m且HM﹥0.4 m时,该公式可以作近似简化为

外飘角ψ可以根据如下三角关系从公式中消去:

可以看出,如果给出船体型线、主尺度以及浮冰的相关性质系数,可以通过芬兰-瑞典规范初步估算冰区船舶在浮冰中的阻力。
2 数值模拟方法
数值模拟方法是一种快捷、低成本的研究方法,随着数值模拟软件的发展和计算机计算效率的提高,数值模拟方法在冰区航行船舶阻力预报研究中的应用变得更加广泛。数值模拟方法不但能够对冰-船相互作用过程进行较为真实的反映,而且不受船型和海域的限制,能够反映出特定变量对于计算结果的影响,有着更大的适用范围和研究价值,是一种拥有良好研究前景的计算方法。
平整冰和碎冰这2种情况是使用数值模拟方法研究船舶在冰区航行中受到阻力时需要主要考虑的冰况。两者和船体发生作用的主要形式也是不相同的,对于平整冰是挤压破坏,对于碎冰冰块是堆积和碰撞,通常采用有限元方法和离散元方法对船舶的海冰阻力进行模拟计算[14]。
2.1 平整冰模拟
在平整冰载荷方面,Kitamura[15]通过 LS-DYNA分析了模型为竖直结构体与一艘集装箱船的船头碰撞过程。Glykas等[16]通过有限元软件ABAQUS分析了船艏与一定大小的冰发生碰撞时弹塑性的变形情况。2008年,Wang Bo等[17]对冰在靠近该 LNG船的3舱室和4舱室进行了碰撞分析,给出了船舶及冰的变形图和所受到的压力云图。2010年,Stine Aas Myhre[18]应用有限元方法分析了LNG船舶与冰的碰撞过程,对碰撞过程中2种冰的模型7个不同的碰撞点都进行了恰当的分析。
2010年,何菲菲[19]以弹性力学理论为基础,从理论角度对计算冰载荷的方法进行了探讨,建立了船体三自由度上的运动方程,在时域内求解了运动响应。使用有限元软件Msc.Dytran对破冰船冲撞冰层的过程进行了数值模拟。计算结果对冰层的破裂形式和过程有着较好的反映,分析了冰载荷的变化趋势,得到船艏应力分布云图。
2.2 碎冰模拟
2.2.1 有限元方法
2010年,Jungyong Wang等[20]初步模拟了“Terry Fox”号破冰船在碎冰条件下的阻力,应用LS-DYNA软件数值计算水动力载荷和船-冰相互作用载荷,对2种不同碎冰浓度(60%和80%)条件下进行数值仿真,并且模拟了一个二维造波机以考虑水-冰相互作用,结果并不理想,但为其他研究人员开辟了新的思路。
2013年Moon-Chan Kim等[21]应用模型试验和LS-DYNA数值模拟2种方法研究一艘自破冰型散货船在碎冰条件下的阻力性能。模拟选择了0.1 m/s和0.3 m/s速度点,分别在60%、80%和90%的碎冰浓度中进行计算。模拟结果与试验结果相比,无论是定性上还是定量上,都有较好的一致性,表明了应用LS-DYNA软件分析碎冰条件下冰区船阻力的可行性。空气、水和船模的模拟示意见图1、2。

图1 空气和水的模拟域Fig.1 Simulated region of water and air

图2 船模网格划分Fig.2 Panel model of icebreaking cargo ship
2.2.2 离散元方法
在碎冰区域,破碎的海冰可以通过离散元方法的离散单元模型合理地进行描述。离散元方法不仅可以描述海冰的材料结构特性,而且能够合理地模拟海冰与船舶结构作用的破碎规律,从而更好地反映冰区航行船舶与碎冰相互作用的过程。
1999年,Hansen等[22]最早采用二维圆盘离散元方法研究碎冰区海冰对船体的作用力。2010年,Zhan等[23-24]采用二维和三维块体离散元软件(DECICE)对破冰船破冰能力和操纵性能进行了数值模拟,对碎冰区的船-冰作用荷载计算进行了探讨。
2013年,李紫麟[25]分析了船舶在碎冰区航行的离散元理论及冰荷载计算方法,建立了浮冰和船体结构相互作用的离散元模型。使用膨胀颗粒方法构造的三维圆盘单元来模拟海冰单元,使用CAD软件构造破冰船的船体模型。船体结构采用三角形单元按一定的排列方式进行构造,通过海冰与船体单元间的接触判断和接触力计算,模拟船-冰相互作用,由此计算船体总冰力。船体结构的离散元模型如图3所示,模拟的碰撞现象如图4所示。

图3 船体结构的离散元模型Fig.3 Discrete element model of the ship hull structure

图4 碎冰与船体结构作用过程中的碰撞现象Fig.4 The collision of ice floe with ship hull
3 试验方法
无论是冰区船初步设计还是冰区船水动力性能研究,冰水池模型试验都是其中必不可少的一步,能够最为真实和准确地反映冰区船航行过程和水动力性能。随着冰区船水动力性能研究工作的深入,试验方法的重要性愈发的突显了。
然而试验方法的进行需要具备一定的条件:冻结模型冰试验必须在冰水池中进行,除了需要具备制冷设备、冰力学性能测量设备等相关配套设备外,对于制冰技术和试验设计也有很高的标准。目前所有的实验室中的模型冰都不能做到和天然冰相同,只能够满足其关键物理性质与天然冰接近。而试验的设计也应根据试验目的的不同进行调整,难度也随之提高。图5为汉堡水池进行的一种基本冰模型试验示意,包括平整冰和碎冰2种工况。

图5 汉堡水池进行的冰模型试验图Fig.5 The ice mode experiment in HSVA
3.1 冻结模型冰试验
冻结模型冰是国际上釆用较多的模型冰类型,当前冻结模型冰的添加剂主要包括:酒精、尿素、盐、糖等。
2010 年,Jeong S[12]等在韩国海上和海洋工程研究所的MOERI冰水池进行了冻结冰中的冰区船模型试验。MOERI冰水池长 42 m,宽 32 m,深2.5 m,主要用来进行破冰船阻力、推进和操纵性试验,以及北极圈部分的平台和浮式结构的冰载荷预测。MOERI冰水池的标准模型船被设计为北极圈附近或其他1年冰覆盖区域的冰区航行船舶,模型被按照 λ=18.667的缩尺比建造(具体参数见表2[12]),目的是为了得到不同厚度和弯曲强度的平面冰阻力预报。

表2 MOERI冰水池试验模型和实船参数Table 2 Parameters of model and full-scale ship in test
这次试验的设计思路基于1992年Spencer[11]提出的冰区船舶航行阻力的分类公式:RT=Row+RB+RC+RBR。为此,分别在敞水区域,平整冰域和碎冰区域进行了试验,以确定阻力的成分。
敞水试验部分,船模以 0.238 m/s,0.357 m/s 和0.476 m/s的速度在水池中行驶(对应实船的2、3、4 kn速度),测量得到的MOERI标准船模的敞水阻力为

破冰阻力并不能直接测量,所以试验中通过在预切割冰中进行试验来去除破冰阻力的部分,如图6所示。通常来说预切割冰区域比船模水线宽度略宽一些。通过预切割冰试验得到预切割冰阻力:

冰浮阻力和船底和肩部的冰浮力有关,通过在一个很低速度下(0.02 m/s)进行预切割冰阻力试验,就可以忽略掉预切割冰阻力中的冰清除阻力和敞水阻力,从而得到冰浮阻力的计算公式:

在预切割冰阻力中去掉敞水阻力和冰浮阻力,得到清除冰阻力:

从总阻力中减去预切割冰阻力,得到破冰阻力。这样最终得到了各种阻力值的数据。

图6 预切割冰试验示意图Fig.6 The pre-sawn ice experiment
3.2 非冻结模型冰试验
伴随着试验技术的发展和冰区试验的要求,各类非冻结合成模型冰也相继问世。非冻结模型冰的优点在于:无需低温制造,试验测试更易控制。20世纪60年代中期,国外学者利用喷到水面上的石蜡模拟平整冰进行了破冰船试验。1999年,王军在国内首次采用石蜡模型冰进行试验,研究冰塞厚度问题[26]。此后,李志军等采用由聚丙烯颗粒、水泥等材料混合而成的DUT-1非冻结模型冰进行冰-结构物试验[27]。
Moon-Chan Kim等[28]进行了在常规PNU拖曳水池使用石蜡和在NRC冰水池使用冻结模型冰的阻力试验,并进行对比,试验现场如图7所示。

图7 PNU拖曳水池和NRC冰水池设施轮廓图Fig.7 The picture of PNU towing tank and NRC ice model tank
试验中使用的非冻结模型冰(石蜡)与冻结模型冰的物理性质的比较见表3[28]。

表3 非冻结模型冰与冻结模型冰的比较Table 3 Comparison of freezing model ice and non-freezing model ice
在PNU拖曳水池非冻结模型冰和NRC冰水池冻结模型冰中分别做了3种不同浓度(90%、80%和60%)碎冰条件下的阻力试验,其中在PNU拖曳水池进行了 5 种不同速度的试验(0.1,0.2,0.3,0.4 和0.6 m/s)。PNU非冻结模型冰和NRC冻结模型冰的试验现象如图8所示。

图8 PNU非冻结模型冰和NRC非冻结模型冰阻力试验简图Fig.8 The experiment in PNU towing tank and NRC ice model tank
试验结果显示,在3种不同浓度(90%,80%和60%)的碎冰条件下,用冻结模型冰和非冻结模型冰测得的阻力值趋势相似。对于80%和60%浓度的碎冰条件,无论是定性上还是定量上,2种模型冰的结果都有很好的一致性。通过这些比较能够得出结论:使用非冻结模型冰代替冻结模型冰进行碎冰条件下的阻力试验是可行的。
4 结论
在当前的冰区船舶阻力预报方法中,以试验为基础的经验公式法是一个传统的重要方法。试验的数据决定了经验公式中的无量纲系数,经验公式中对于航行阻力的分类方法反过来会影响试验的设计。而数值模拟方法作为一种新兴方法,有着很高的研究价值和应用前景。
1)经验公式方法在预报拥有大量试验数据的船型时,有着良好的预报结果。其劣势在于过于依靠实船试验数据,不能全面的表现船型、冰况等因素对于阻力的影响,在新船型的开发和计算方面有着不足之处。
2)数值模拟方法是一种快捷、低成本的冰区船舶航行阻力预报方法。相对于经验公式方法,数值模拟在研究冰-船作用现象、新船型开发问题上有着很大的优势,不过目前数值模拟方法的精确性和可靠性也有着提高的空间,需要依靠传统的经验公式和试验方法进行修正。
3)试验方法是无疑是研究冰区船舶航行阻力的最重要的方法,通过船模试验得到冰区船舶航行中与冰相互作用的现象和阻力数据。由种种实际条件的限制,尤其是冻结模型冰的制取和性质检测,影响了冻结冰模型试验的进行。因此非冻结模型冰试验无疑能够为进行冰区船舶模型试验提供一种新的思路和可能。
4)在冰区船阻力性能研究中,不应当孤立地使用经验公式、数值模拟或试验方法,3种方法各有适用范围和特点,相互结合,对比研究,才能在该领域有所突破。
[1]CORLETT E C B,SNAITH G R.Some aspects of icebreaker design[J].Transactions of the Royal Institution of Naval Architects,1964,106:389.
[2]霍夫曼,钱文豪.船舶在冰区航行的阻力和推进性能[J].船舶,1990(6):31-34.
HOFFMAN D,QIAN Wenhao.Resistance and propulsion performance of ship in ice[J].Ship,1990(6):31-34.
[3]JANSSON J E.Ice-breakers and their design[M].[s.l.]:European Shipbuilding,1956.
[4]KASHTELJAN V I,POZNJAK I I,RYBLIN A J.Ice resistance to motion of a ship[M].Leningrad:Marine Computer Application Corporation,1969.
[5]VANCE G P.A modeling system for vessels in ice[R].Kingston:University of Rhode Island,1975.
[6]LEWIS J W,EDWARDS R Y.Methods for predicting icebreaking and ice resistance characteristics of icebreakers[C].Annual Meeting.Jersey City,USA,1970,78:213-249.
[7]ENKVIST E.On the ice resistance encountered by ships operating in the continuous mode of ice breaking,No.24[R].Helsinki:Swedish Academy of Engineering Sciences,1972.
[8]LINDQVIST,GUSTAV.A straight forward method for calculation of ice resistance of ships[C]//Port and Ocean Engineering under Arctic Conditions.Luleaa,Sweden,1989:722.
[9]RISKA K,WILHELMSON M,ENGLUND K,et al.Performance of merchant vessels in ice in the Baltic,winter navigation research board NO.52[R].Helsinki:Finnish Maritime Administration,1997.
[10]SPENCER D,JONES S J.Model-scale/full-scale correlation in open water and ice for Canadian coast guard"RClass"icebreakers[J].Journal of Ship Research,2001,45(4):249-261.
[11]SPENCER D.A standard method for the conduct and analysis of ice resistance model tests[J].Proc of the 23rd ATTC Symp,1992:301-307.
[12]JEONG S Y,CHOI K.A review on ice resistance prediction formula for icebreaking vessels[C]//The Nineteenth International Offshore and Polar Engineering Conference.International Society of Offshore and Polar Engineers.[s.l.],2009:587-592.
[13]Finnish-Swedish Ice Class Rules[S].Finnish and Swedish Maritime Administration,2002.
[14]ZHOU L,SU B,RISKA K,et al.Numerical simulation of moored structure station keeping in level ice[J].Cold Regions Science and Technology,2012,71:54-66.
[15]KITAMURA O.Comparative study on collision resistance of side structure[J].Marine Technology,1997,34(4):293-308.
[16]GLYKAS A,DAS P K.Energy conservation during a tanker collision[J].Ocean Engineering,2001,28(4):361-374.
[17]WANG B,YU H C,BASU R.Ship and ice collision modeling and strength evaluation of LNG ship structure[C]//ASME 2008 27th International Conference on Offshore Mechanics and Arctic Engineering.American Society of Mechanical Engineers.Estoril,Portugal,2008:911-918.
[18]MYHRE S A.Analysis of accidental iceberg impacts with membrane tank LNG carriers[D].Trondheim:Norwegian University of Science and Technology,2010:1-40.
[19]何菲菲.破冰船破冰载荷与破冰能力计算方法研究[D].哈尔滨:哈尔滨工程大学,2011:23-60.
HE Feiei.A computational method for ice-breaking loads and capability of icebreaker[D].Harbin:Harbin Engineering University,2011:23-60.
[20]WANG J,DERRADJI A A.Numerical prediction for resistance of Canadian icebreaker CCGS Terry Fox in level ice[C]//ICSOT 2009:Ice Class Vessels,2011:72.
[21]KIM M C,LEE S K,LEE W J,et al.Numerical and experimental investigation of the resistance performance of an icebreaking cargo vessel in pack ice conditions[J].International Journal of Naval Architecture and Ocean Engineering,2013,5(1):116-131.
[22]HANSEN E H,LØSET S.Modelling floating offshore units moored in broken ice:model description[J].Cold Regions Science and Technology,1999,29(2):97-106.
[23]ZHAN D,AGAR D,HE M,et al.Numerical simulation of ship maneuvering in pack ice[C]//ASME 2010 29th International Conference on Ocean,American Society of Mechanical Engineers,2010:855-862.
[24]LAU M,LAWRENCE K P,ROTHENBURG L.Discrete element analysis of ice load on ships and structures[J].Ships and Offshore Structure,2011,6(3):211-221.
[25]李紫麟.船舶在碎冰区航行的离散元模型及冰荷载分析[D].大连:大连理工大学,2013:1-48.
LI Zilin.Analysis of ship maneuvering performances and ice loads on ship hull with discrete element model in brokenice field[D],Dalian:Dalian University of Technology,2013:1-48.
[26]王军.初始冰塞厚度与水流条件及冰流量关系的试验研究[J].水利水运科学研究,1999(4):385-389.
WANG Jun.A study on the relationship about initial ice jam thickness with its stream conditions and ice discharge[J].Journal of the Hydro Science Study,1999(4):385-389.
[27]李志军,李广伟,沈照伟,等.DUT-1模型冰的物理性能和弹性模量[J].自然科学进展,2000,10:69-73.
LI Zhijun,LI Guangwei,SHEN Zhaowei,et al.Physical properties and elastic modulus of DUT-1 model ice[J].Journal of Progress in Natural Science,2000,10:69-73.
[28]KIM M C,LIM T W,JO J C,et al.Comparison study on the propulsion performance for icebreaker with synthetic ice and refrigerated ice[J].Journal of Ocean Engineering and Technology,2009,23(1):129-134.

