时敏制导炸弹离散自适应滑模BTT自动驾驶仪设计

李伟明，白宏阳，辛明瑞，申景诗

（1.山东航天电子技术研究所，山东烟台264003；2.南京理工大学能源与动力工程学院，江苏南京210094）

时敏制导炸弹离散自适应滑模BTT自动驾驶仪设计

李伟明1，2，白宏阳2，辛明瑞1，申景诗1

（1.山东航天电子技术研究所，山东烟台264003；2.南京理工大学能源与动力工程学院，江苏南京210094）

为提高航空时敏制导炸弹控制系统的鲁棒性能，增强其大空域作战能力，将参数估计与离散滑模控制相结合，提出了一种适用于航空时敏制导炸弹倾斜转弯（bank-to-turn，BTT）自动驾驶仪的离散自适应滑模设计方法。建立了包含参数摄动项的BTT控制仿射模型，针对弹体气动对称与交叉耦合等特性，利用反馈线性化方法实现了原系统的解耦控制，并得到了参数化的离散滑模控制律；基于Lyapunov稳定性理论设计了控制器参数的自适应规律，有效克服了各动力学系数偏差引起的不确定扰动。仿真结果表明，所设计的离散自适应滑模BTT控制系统实现了各通道的解耦控制，能有效解决含有较大程度气动不确定性时炸弹的指令跟踪控制问题，并且消除了常规滑模控制的抖振现象。

时敏制导炸弹；倾斜转弯自动驾驶仪；离散趋近律；离散自适应滑模控制

0 引 言

与常规炸弹相比，航空时敏制导炸弹具有射程远、精度高等优点；同时，为能对时敏目标实施有效打击，其在弹道末段采用倾斜转弯（bank-to-turn，BTT）控制模式，同时利用双向数据链路进行“人在回路”的目标识别与制导方式切换，具有较大的灵活性，可满足未来联合信息作战的需求。然而，其控制与制导模式、结构特点给系统带来较强的通道耦合、传输噪声及气动参数摄动，故近年来国内外相关学者在解决上述问题中多采用如鲁棒［1］、反演［2］、动态逆［3-4］以及滑模控制［56］等非线性控制方法。其中，滑模控制（sliding mode control，SMC）因其克服参数摄动的良好鲁棒性能而被广泛应用于现代制导弹箭的非线性控制系统设计之中［7-10］。

然而，在现代制导弹箭的实际应用过程中，弹上控制单元按给定时钟节拍进行指令解算，解算方法及采样频率对控制效果影响显著，而基于连续时间系统理论设计的弹载控制器的控制性能将有所限制。因此，为使实际控制性能接近于理论仿真结果，研究制导炸弹BTT自动驾驶仪的离散滑模控制（discrete-time sliding mode control，DSMC）方法具有重要的工程价值。文献［11］设计了具有模型不确定和时变干扰的线性离散时滞网络导弹控制系统的离散滑模控制器，有效降低了系统抖振。文献［12］则着重分析了快速输出采样技术对导弹姿态离散变结构控制系统的影响。

由于连续时间系统的SMC理论难以直接应用于实际的离散时间系统设计之中，故本文在BTT控制仿射模型中考虑参数摄动项，利用反馈线性化方法对原系统解耦并推导了离散虚拟控制律，并在文献［11- 12］控制算法的基础上，将自适应控制与DSMC进行结合，设计了时敏制导炸弹的离散自适应滑模（discrete-time adaptive sliding mode control，DASMC）BTT自动驾驶仪。仿真结果表明，该设计方法可显著减小控制抖振，改善闭环系统的动态特性，进而验证了该自动驾驶仪的稳定性与抑制参数摄动的鲁棒性能。

1 BTT控制仿射模型建立

忽略攻角α、侧滑角β等二阶小量影响，不考虑舵机动力学特性，建立如下包含参数不确定性和外部干扰的BTT控制仿射模型方程：

式中，状态变量x＝［γ，ny，nz，ωx，ωz，ωy］T；控制输入u＝［δx，δz，δy］T；参考输出y＝［γr，nyr，nzr］T为外部干扰。估计函数向量及估计增益矩阵^G（x）分别为

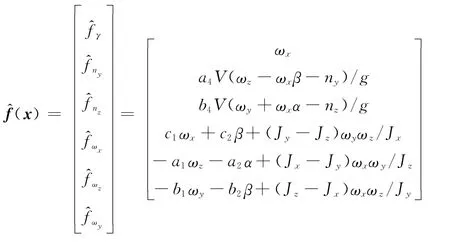
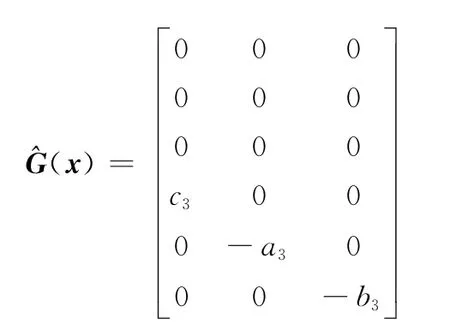
式中，Δai、Δbi及Δcj为各动力学系数的偏差项。

2 制导炸弹离散自适应滑模BTT控制器设计

2.1 精确反馈线性化解耦

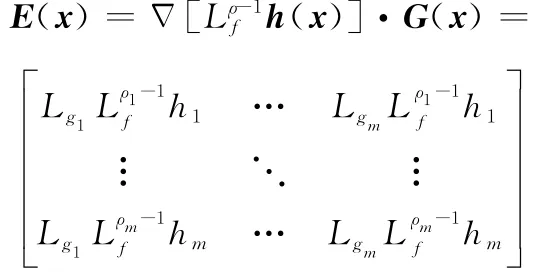
可逆，因此，通过非线性输入变换可得到系统的解耦控制律为

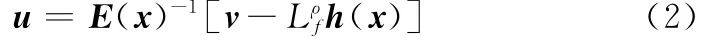
式中，E（x）为解耦矩阵。则式（1）所示的多输入多输出非线性系统则转化为m个独立的线性动态方程

易知，式（3）中m＝3、ρi＝2，即可解耦为3个独立的二阶子系统进行控制，则系统式（1）的Lyapunov微分系数向量可表示为

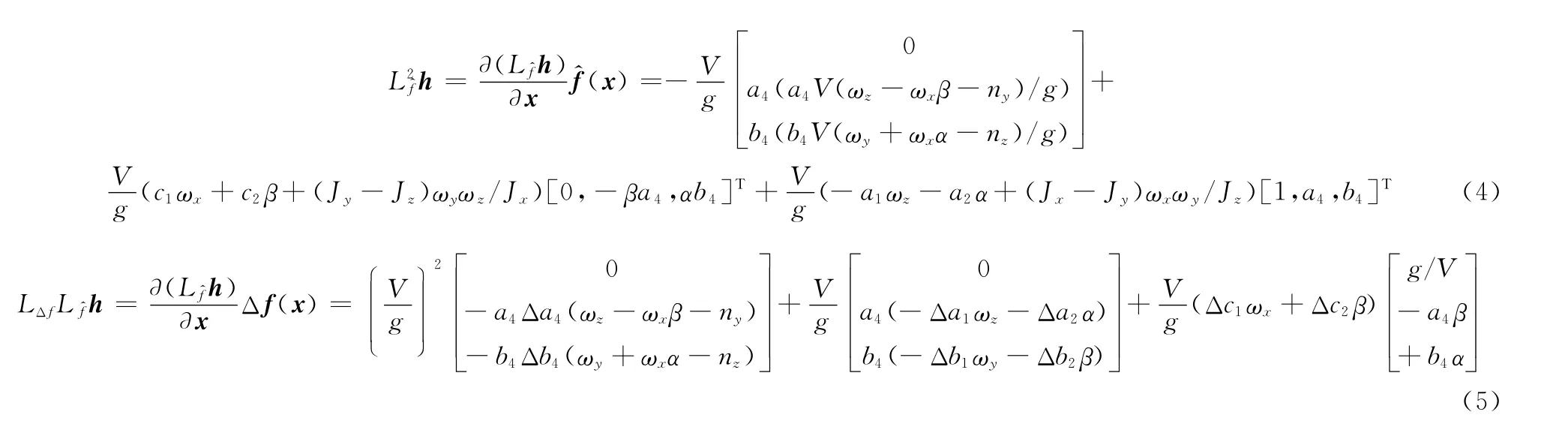
非线性解耦矩阵可表示为

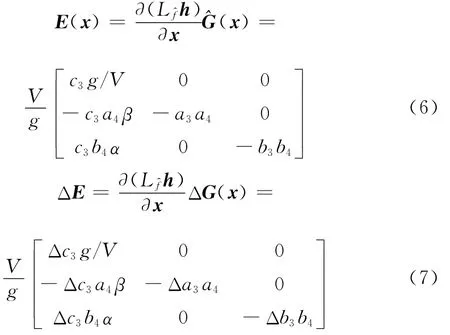
2.2 离散滑模BTT控制器设计

设原连续时间系统的状态空间矩阵（A，B）完全可控，则系统内任意相邻采样周期［k T，（k＋1）T］内的离散化状态转移矩阵及增益矩阵可表示为

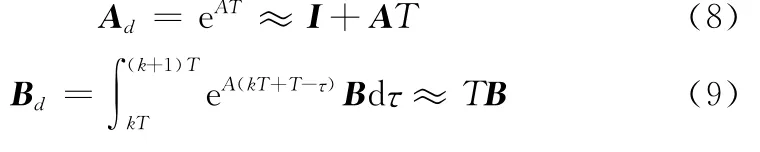
经反馈线性化解耦后，系统的输出跟踪指令在新坐标系下可表示为

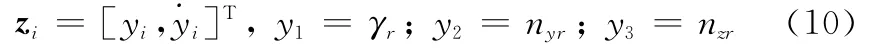
假设系统式（1）中的不确定性扰动项满足｜d～i｜＜Di（∀Di＞0），则式（3）所示线性子系统可离散化表示为

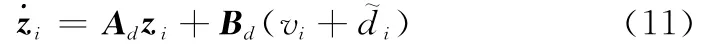
式中，系数矩阵表示为

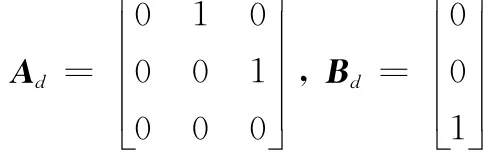
则该制导炸弹BTT控制系统各解耦子系统的离散化状态方程可描述为

其中，模型不确定扰动项可表示为

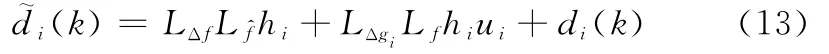
式中，di（k）为非参数外部扰动。

设λ＞0，C＝［λ，1］，结合非线性离散状态方程式（12），选取如下线性切换函数作为系统式（1）的滑模面S：

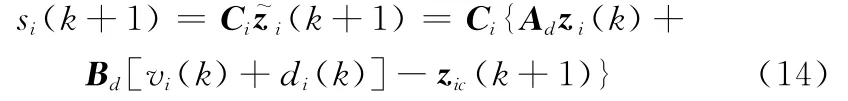
式中，zic（k＋1）为（k＋1）T时刻的输出指令。

由于受采样周期T的影响，滑模运动通常在滑模面上反向穿越，为使从任意初始状态出发的离散时间系统式（12）的运动于有限时间内收敛到准滑动模态，定义一个包围切换面的切换带［14］（其带宽为｜2Δ｜）

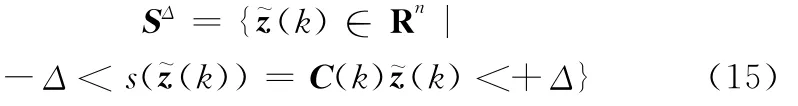
为对滑模控制抖振加以抑制，通过边界层对控制的不连续性进行平滑［15］。同时假设采样时间较小，则有CiBid≈T，故可选取离散化饱和型指数趋近律

式中，ε＞0为切换增益；q＞0为趋近律系数，且满足1－qT＞0；μ为边界层厚度。

综合式（12）、式（14）及式（16），可得离散滑模虚拟控制律为

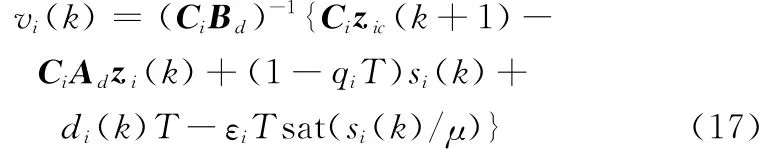
式中，子系统切换增益应设置为εi≥Di＋ηi（ηi＞0）。

由式（15）、式（17）可计算各解耦子系统切换面的切换带宽

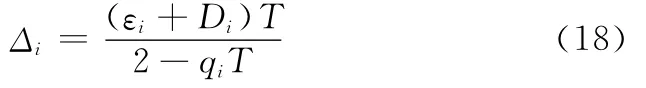
2.3 参数自适应律设计及稳定性分析

为解决在采样频率受限情况下较大模型参数摄动带来的滑动模态不收敛问题，考虑在离散滑模控制中引入自适应控制机制，同时引入零阶保持器以确保系统各状态量在同一采样周期内维持不变，其离散自适应滑模BTT控制系统结构如图1所示。

将式（13）改写为参数误差向量形式

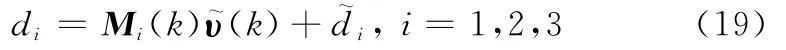
即

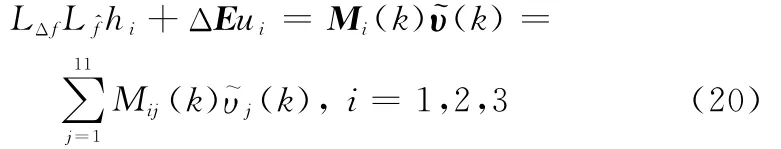
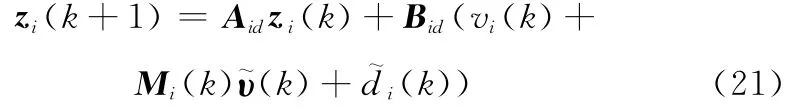
则式（14）可进一步改写为

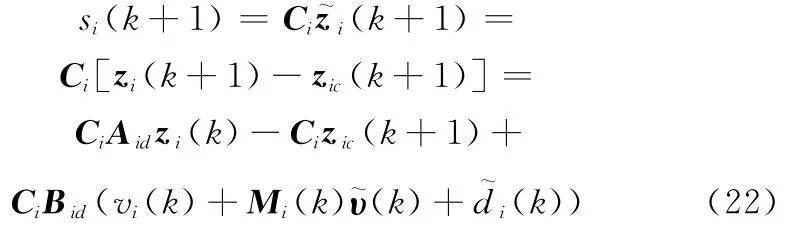
采用虚拟控制律式（17），代入式（21）可得

则增量Δsi（k＋1）可表示为

式中

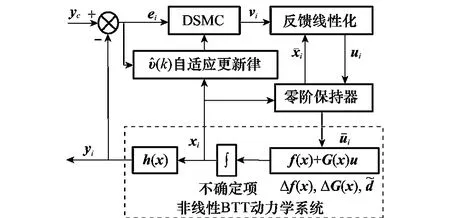
图1 炸弹离散自适应滑模BTT控制系统结构框图

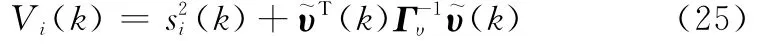
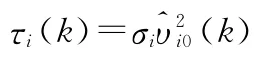
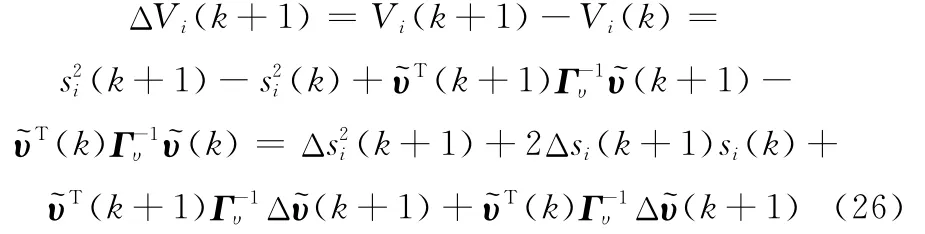
采用式（17）的离散滑模虚拟控制律，并设计参数自适应更新律为

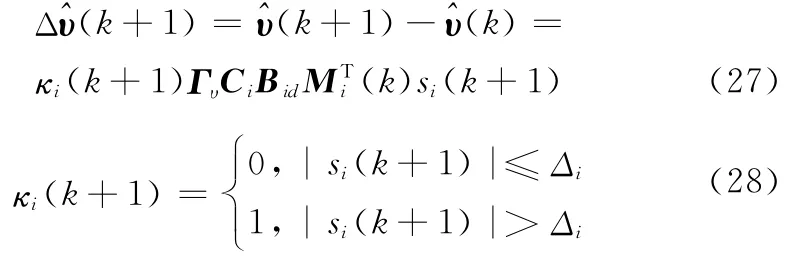
式中，Δi为各解耦子系统切换面的切换带宽。当si（k）在切换带以内（k＋1）＝0，参数停止更新，参数误差项趋于平稳。而在切换带以外时，激发对象模型参数自适应更新规律。另外，趋近律系数qi、采样时间T及切换增益εi等均对指令跟踪精度及系统稳定性有影响，如qi主要影响切换函数的动态过程；T则与模态收敛速度成反比，与穿越理想滑模面的次数成正比，随着采样率的下降，系统稳定性也变差；εi则反应了克服系统参数摄动及外部干扰等不确定性的能力，当εi＞，系统状态满足｜si（k）｜＞Δi时，采用传统的纯滑模控制将使得

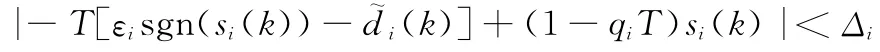
而当｜si（k＋1）｜＞Δi时，则有

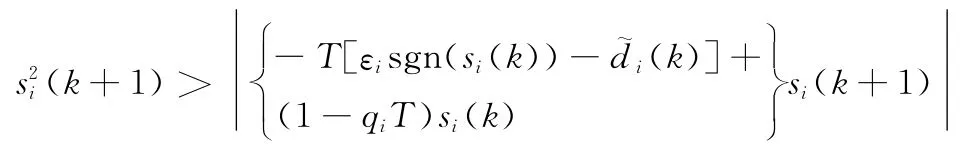
即ΔVi（k＋1）≤0，从而证明控制系统稳定，误差可有效收敛。

3 离散自适应滑模控制器性能仿真与分析

为验证离散参数自适应更新律对降低系统控制抖振、抑制系统参数漂移以及对参数摄动的鲁棒性能，进行两组对比仿真：在DSMC方法中设定采样周期T＝10 ms，滑模面增益λ1＝6.5、λ2＝λ3＝8.0，切换增益ε1＝0.25、ε2＝ε3＝0.5，ηi＝0.1，趋近律系数qi＝5，边界层厚度μ＝0.05、外界不确定干扰上界D1＝0.05、D2＝D3＝0.075；而在DASMC方法中，控制器参数不变，自适应因子设定为σ1＝0.7、σ2＝σ3＝0.85。

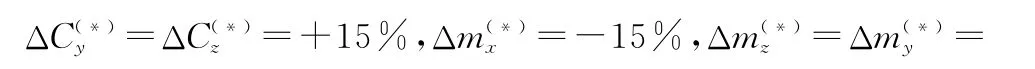
表1 弹体各静参数标准值

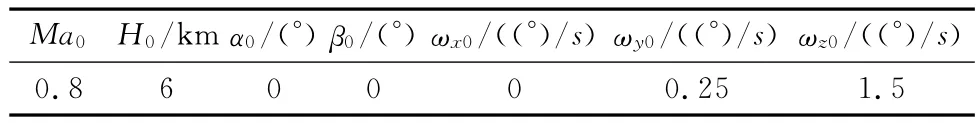
表2 弹道仿真各初始参数

过载指令跟踪响应对比曲线如图2所示，其中法向过载nyc为正弦输入，侧向过载nzc则为零输入。对γc＝60°的滚转角指令的跟踪响应曲线如图3所示。由图中可看出，当T相同时，DASMC方法对指令跟踪的快速性更好，跟踪精度也更高。

对应攻角及侧滑角状态响应曲线如图4所示，从图中可以看出，在气动参数相对于先验值存在摄动的情况下，DASMC方法可使侧滑角保持在±3°以内，满足BTT控制的性能要求。而DSMC方法由于控制抖振的存在，使得攻角及侧滑角状态量变化趋势波动较大，特别是侧滑角，由于对过载指令nzc跟踪误差的积累，使得侧滑角的值在跟踪后期不断变大，超出BTT控制对于偏航通道的约束要求。

图2 过载指令跟踪响应

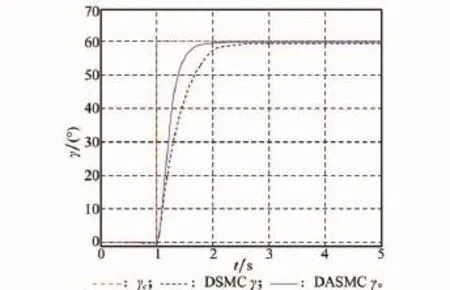
图3 滚转角指令跟踪响应

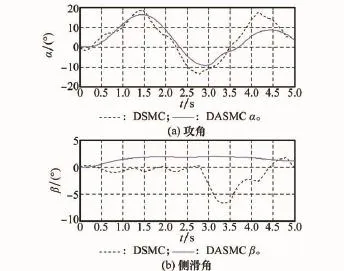
图4 攻角与侧滑角状态响应对比曲线

图5和图6为三通道角速率状态响应对比曲线，从图中可以看出，采用DSMC方法时，由于各通道控制舵偏存在不同程度的控制抖振，因而对应通道的角速率状态量存在着一定程度的振荡。而采用DASMC方法时，角速率状态量变化则较为平缓，振荡现象得以改善。

图7和图8显示了采用两种方法时的舵偏量对比曲线，采用DSMC方法时，舵偏量存在明显的控制抖振，而DASMC方法可对模型参数进行较好的自适应调整，从而有效消除高频抖振，降低跟踪误差。图9和图10分别为两种方法下对应的滑模面切换函数对比规律曲线。图11～图13分别为在采样周期相同时，各通道指令跟踪的相轨迹对比曲线。从图中可以看出，采用DASMC方法时，各通道轨迹均能有效地收敛于滑模面附近较小的区域，进而使得切换函数能收敛于较小的切换带内，从而保证稳态时系统沿准滑模面运动，达到跟踪控制的目的。在趋近律速率参数qi相同的情况下，两种方法中系统达到滑模面的速度几乎相同。而由于采样周期的影响，采用DSMC方法时，由初始状态出发的滑模运动在切换面上来回反向穿越，进而对跟踪精度造成一定的损失。

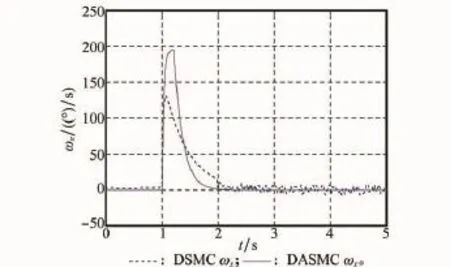
图5 滚转角速率状态响应对比曲线

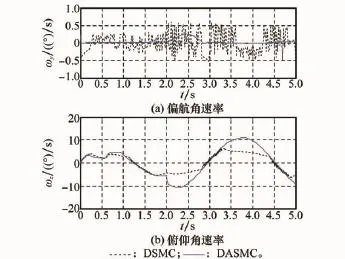
图6 偏航、俯仰角速率状态响应对比曲线

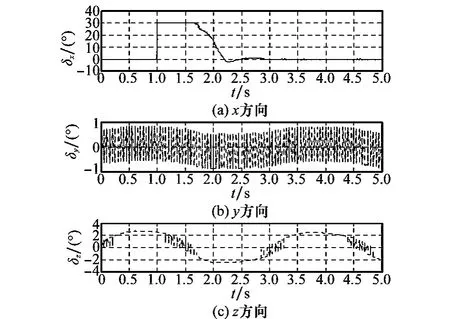
图7 舵偏曲线（DSMC）

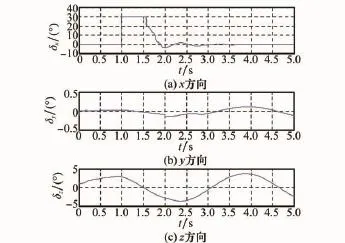
图8 舵偏曲线（DASMC）

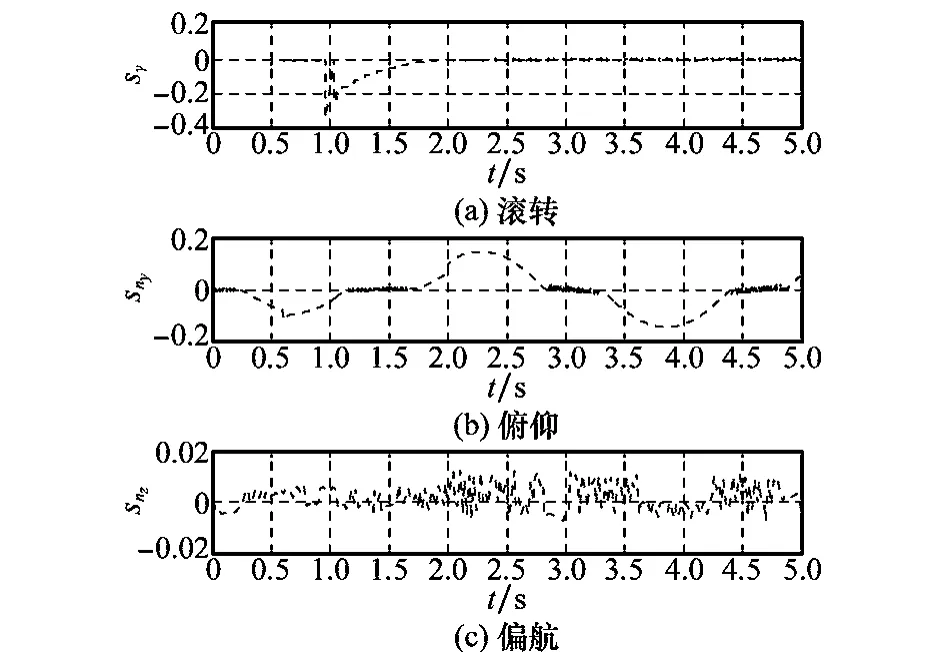
图9 DSMC切换函数曲线

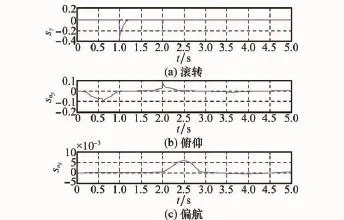
图10 DASMC切换函数曲线

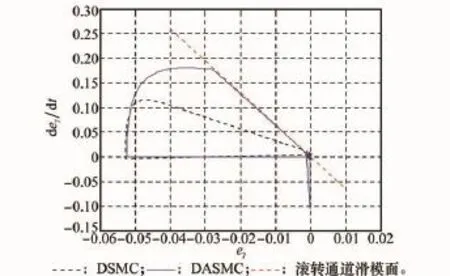
图11 滚转通道滑模面相轨迹对比曲线

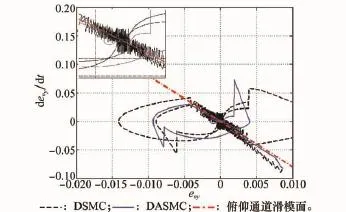
图12 俯仰通道滑模面相轨迹对比曲线

图13 偏航通道滑模面相轨迹对比曲线

4 结束语

本文研究了航空时敏制导炸弹BTT自动驾驶仪的离散自适应滑模设计方法，建立了考虑参数摄动项的BTT仿射模型，在利用反馈线性化理论对原非线性耦合之后，通过离散化状态转移矩阵及增益矩阵对子系统进行离散化处理。基于离散饱和趋近律推导了虚拟控制律，之后将参数自适应律与离散滑模控制律相结合，设计了该制导炸弹的BTT自动驾驶仪，以消除抖振，同时满足对参数时变特性的自适应估计性能。对比仿真结果表明，当气动参数存在较大摄动时，所设计的离散自适应BTT控制系统满足了对指令跟踪的鲁棒性能。该设计方法可为控制系统的工程化实现提供一定的理论参考。

［1］Lee C H，Chung M J.Gain-scheduled state feedback control design technique for flight vehicles［J］.IEEE Trans.on Aerospace and Electronic Systems，2001，37（4）：173- 182.

［2］Lee T，Kim Y D.Nonlinear adaptive flight control using backstepping and neural networks controller［J］.Journal of Guidance，Control and Dynamics，2001，24（4）：675- 682.

［3］Zheng J H，Luan Z W，Cui P Y，et al.Autopilot design for a bankto-turn missile using the inverse nyquist array method［C］∥Proc.of the AIAA Guidance，Navigation and Control Conference，1993：1642- 1647.

［4］Chris M M，Zhu J J，Zhang T Q.Bank-to-turn roll-yaw-pitch autopilot design using dynamic nonlinear inversion and PD-eigenvalue assignment［C］∥Proc.of the American Control Conference，2000：1359- 1364.

［5］Tong C X，Wang Z J，Zhang T Q.Decoupling system design based on variable structure system for BTT missile［J］.Journal of Astronautics，2006，27（1）：27- 30.（童春霞，王正杰，张天桥.BTT导弹的变结构解耦控制系统设计［J］.宇航学报，2006，27（1）：27- 30.）

［6］Zhang Y X，Dong C Y，Wang Q，et al.Decentralized adaptive sliding mode decoupling control scheme for bank-to-turn missile［J］.Acta Armamentarii，2010，31（7）：906- 910.（张颖昕，董朝阳，王青，等.倾斜转弯导弹的分散自适应滑模解耦控制方案［J］.兵工学报，2010，31（7）：906- 910.）

［7］Shkolinikov I A，Shtessel Y B.Aircraft non-minimum phase control in dynamic sliding manifolds［J］.Journal of Guidance，Control，and Dynamic，2001，24（3）：566- 567.

［8］Singh S N，Steinberg M L，Page A B.Nonlinear adaptive and sliding mode flight path control of F／A-18 model［J］.IEEE Trans.on Aerospace and Electronic Systems，2003，39（4）：1250- 1261.

［9］Wu P，Yang M.Integrated guidance and control design for missile with terminal impact angle constraint based on sliding mode control［J］.Journal of Systems Engineering and Electronics，2010，16（4）：56- 60.

［10］Shtessel Y B，Shkolnikov I A，Levant A.Guidance and control of missile interceptor using second-order sliding modes［J］.IEEE Trans.on Aerospace and Electronic Systems，2009，45（1）：110- 124.

［11］Yu C L，Xu H L.Discrete-time sliding mode controller for linear time-varying systems with network induced time delay and application to missile attitude control system［J］.Aerospace Control，2008，26（6）：33- 37.（禹春来，许化龙.非匹配不确定网络离散滑模控制及在导弹姿态控制中的应用［J］.航天控制，2008，26（6）：33- 37.）

［12］Menon P K，Sweriduk G D，Vaddi SS.Nonlinear discrete-time design methods for missile flight control systems［C］∥Proc.of the AIAA Guidance，Navigation，and Control Conference，2004：AIAA 2004- 5326.

［13］Tang Y H.BTT missile robust H∞autopilot design［D］.Xian：Polytechnical University，2004.（汤一华.BTT导弹鲁棒H∞自动驾驶仪［D］.西安：西北工业大学，2004.）

［14］Gao W B.Variable structure control theory and design method［M］.Beijing：Science Press，1996.（高为炳.变结构控制理论与设计方法［M］.北京：科学出版社，1996.）

［15］Yang R J，Yang H，Liang X D，et al.Control system design for guidance projectile based on adaptive sliding mode control［J］.Journal of Ballistics，2012，24（3）：75- 79.（杨荣军，杨桦，梁旭栋，等.基于自适应滑模的制导炮弹控制系统设计［J］.弹道学报，2012，24（3）：75- 79.）

白宏阳（1985- ），通信作者，男，讲师，博士，主要研究方向为先进弹箭控制、GPS／INS组合导航、传递对准系统设计。

E-mail：hongyang＠njust.edu.cn

辛明瑞（196-1- ），男，研究员，博士，主要研究方向为制导控制系统设计、航天器导航、通信系统设计。

E-mail：pachyrhizuscat＠163.com

BTT autopilot design for time-sensitive guided bombs based on adaptive discrete-time sliding mode control

LI Wei-ming1，2，BAI Hong-yang2，XIN Ming-rui1，SHEN Jing-shi1
（1.Shandong Aerospace Electro-Technology Institute，Yantai 264003，China；2.School of Energy and Power Engineering，Nanjing University of Science and Technology，Nanjing 210094，China）

In order to improve the robustness performance and enhance the large-space combat capability of the airborne time-sensitive guided bombs，a discrete-time adaptive bank-to-turn（BTT）autopilot design method is proposed by combining a parameter estimation scheme with the discrete-time sliding mode control.The BTT control affine system containing parameter perturbation items is modeled.Meanwhile，aiming at the aerodynamic parameter symmetry and cross coupling characteristics，input-output feedback linearization is utilized to decouple the system，and a parametric discrete-time sliding mode control law is obtained.The parametric adaptation law designed based on Lyapunov stability theory can overcome the uncertain disturbances caused by aerodynamic coefficient deviation items effectively.The simulation results indicate that the adaptive discrete-time sliding mode BTT control system proposed is robust to the large-scale aerodynamic parametric uncertainty and has excellent dynamic tracking performance with no control chattering.

time-sensitive guided bombs；bank-to-turn（BTT）autopilot；discrete reaching law；discretetime adaptive sliding mode control

TP 413

A

10.3969／j.issn.1001-506X.2015.11.24

李伟明（1985- ），男，工程师，博士，主要研究方向为飞行力学、先进弹箭制导与控制技术。

E-mail：lee_weiming＠163.com

1001-506X（2015）11-2579-07

2014- 12- 24；

2015- 03- 25；网络优先出版日期：2015- 05- 13。

网络优先出版地址：http：／／www.cnki.net／kcms／detail／11.2422.TN.20150513.1130.006.html

江苏省自然科学基金（BK20140795）；总装预研基金（9140A31010114JB25465）；中国航空科学基金（20145159002）；中国航天五院CAST创新基金（CAST2014－27）；中国博士后科学基金（2014 M562568）资助课题