分布式小卫星联合多普勒解模糊SAR成像
张 龙,苏 涛,刘 峥,贺小慧
(1.西安电子科技大学雷达信号处理国家重点实验室,陕西西安710071; 2.西安工程大学电子信息学院,陕西西安710048)
分布式小卫星联合多普勒解模糊SAR成像
张 龙1,2,苏 涛1,刘 峥1,贺小慧1,2
(1.西安电子科技大学雷达信号处理国家重点实验室,陕西西安710071; 2.西安工程大学电子信息学院,陕西西安710048)
针对分布式小卫星体制提出联合多普勒解模糊SAR成像算法,实现低方位重频采样下的高分辨宽测绘带SAR成像。该算法可以有效校正垂直基线,进而解决其对多普勒解模糊性能的影响。不但校正了垂直基线对应的非空变部分和空变部分,而且结合多普勒解模糊算法校正了残余的垂直基线相位项,从而可以保证多普勒解模糊算法精确实现。另外,针对算法精度进行详细分析,增强文章的工程应用价值。最后,利用仿真实验数据验证算法的有效性。
分布式小卫星;合成孔径雷达;基线校正;多普勒解模糊
0 引 言
星载SAR具有观测范围广、运行轨道稳定、隐蔽性强等特点,因此一直以来都是SAR成像应用的热门领域[15]。当前随着科技发展的日新月异,对星载SAR成像性能指标的要求越来越高。更高的空间分辨率、更广的观测范围、更短的重访周期越来越受到各国星载SAR研究单位和学者的青睐[68]。利用传统星载SAR实现高分辨宽测绘带SAR成像存在最小天线面积的限制[9],即方位高分辨和距离宽测绘带要求天线方位和距离的孔径长度要小,但是较小的天线尺寸却无法满足星载SAR远距离回波信噪比的要求。
为了解决这样的矛盾,研究学者提出星载多通道体制实现高分辨宽测绘带SAR成像[1011]。该体制将传统大天线分割成若干子孔径天线,可以兼顾方位高分辨和距离宽测绘带。然而这样的体制系统设计复杂度较高,且孔径间基线较短,空间自由度有限,性能提升有限。为了进一步提升星载SAR的多样性功能,分布式小卫星体制于20世纪90年代被提出[12-13]。该体制由若干颗小卫星作为伴随卫星和一颗中心卫星(中心卫星可以是一颗大卫星,也可以是一个“虚拟”中心)组成小卫星星座。这些小卫星按照一定的构型运行,并且相互协同工作完成某种任务,其功能可以远远超过传统单颗大卫星。并且系统设计复杂度大大降低,发射和运行成本也远低于传统的单颗大卫星。
实现高分辨宽测绘带SAR成像通常采用低方位重复采样频率,保证回波距离向不模糊,但是方位向多普勒模糊无法避免。因此要求后续成像算法考虑多普勒解模糊,即利用信号处理手段重构不模糊的多普勒频谱。多普勒解模糊算法大致可以分为两类:非自适应[14]和自适应[15-17]。其中典型的非自适应多普勒解模糊方法为空域滤波[14],该方法直接在空时谱上对某一多普勒单元内的特定多普勒频率进行滤波,提取期望信号,并抑制模糊信号至能量零点。空域滤波解多普勒模糊在没有系统噪声和基线误差情况下可以实现性能最优。另外一类自适应多普勒解模糊方法,典型代表是Capon空间谱估计方法[15]。该方法并非将模糊信号抑制至能量零点,而是将其抑制到噪声功率以下,这样Capon解多普勒模糊方法具有更好的容噪性和基线误差容忍度,因此稳健性更佳。针对分布式小卫星实现高分辨宽测绘带SAR成像,由于小卫星星座具有更大的空间自由度,可以提供更大的星间基线,因此可以实现更加优异的成像性能。尤其对于存在三维基线的分布式小卫星SAR系统,水平基线(沿航线基线)为多普勒解模糊提供空间采样,而垂直基线(垂直航线基线)为干涉SAR(InSAR)或动目标等功能实现提供条件。
本文设计联合多普勒解模糊SAR成像可以实现低方位重频采样下的多普勒解模糊SAR成像。首先针对三维基线下的分布式小卫星阵列建立模型,并讨论阵列等效等问题,简化问题模型。然后针对垂直基线进行推导,将其分解为非空变部分和空变部分,并分别校正。另外,考虑到多普勒频率对应波束方位角,即多普勒模糊对应波束方位角上的能量模糊,因此结合多普勒解模糊校正残余垂直基线相位项,保证基线误差精度满足多普勒解模糊性能要求。最后,针对联合多普勒解模糊算法进行仿真实验分析,验证该算法的有效性。
1 分布式小卫星SAR信号模型
分布式小卫星在轨运行示意图如图1所示。尽管实际卫星轨道为近似椭圆,并且由于地球自转会导致星间回波不一致,但是依据文献[18]可以将地球惯性坐标系下同轨分布式小卫星星座等效至地球固定坐标系下轨道平行的分布式小卫星星座,并基于子孔径坐标系补偿轨道曲率,从而可得等效后的分布式小卫星星座在直线轨道下运行示意图如图1所示。该星座星间同时存在三维基线,且等效地球固定坐标系X-Y-Z下地面上的观测场景固定不动,而小卫星星座相对运动,星座运行等效速度为veq。分布式小卫星星座由Q颗小卫星组成。
通常情况下,分布式小卫星SAR收发分置,即一发多收或多发多收,通过相互协同和信号处理完成传统单颗大卫星无法完成的任务。为了便于信号分析和处理,一般将收发的双基雷达构型等效为在发射和接收卫星中点处自发自收,并称该中点为等效相位中心[14]。如此等效在发射和接收卫星间距较短时成立,如果间距超过百米,则需要对回波信号乘以一个常数相位exp(jπD2/2Rsλ)才能保证等效相位中心继续有效,其中D表示两星间距在雷达视线方向上的投影,Rs表示等效相位中心到场景中心的参考距离,λ表示雷达波长。如果小卫星间距进一步增大,按照以上相位中心等效的方法精度会明显下降。为了有效提高双基构型等效单基的精度,可以采取等效相位中心定在双基角分线上,然后通过预滤波的方法补偿双基效应带来的包络偏移和相位调制[19]。经过上述等效相位中心处理,分布式小卫星SAR星座收发分置的双基构型可以等效为在各自等效相位中心处自发自收工作。由此,图1中Q颗小卫星构成Q个等效相位中心,其中第q个等效相位中心标记为(Xq, Yq,Zq)。
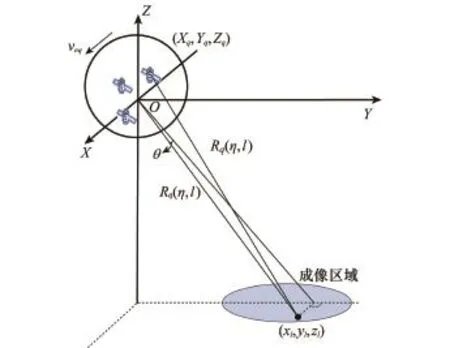
图1 分布式小卫星SAR几何模型
除此之外,为了避免分布式小卫星星间发生碰撞,保证在轨运行的安全性,小卫星间距,即基线,通常较大。其中沿航向基线通常在几百米甚至一公里,而垂直航线平面上的基线则相对较小,为几十米至一百米。因此空间运行的分布式小卫星星座一般超稀疏分布,不仅仅为了卫星运行的安全性考虑,同时较大的基线为高性能SAR成像提供了足够的空间自由度和系统设计冗余度。但是超稀疏分布的小卫星SAR阵列会影响回波信号的相干性,因此需要对超稀疏分布的小卫星SAR阵列进行等效。根据SAR理论可知,SAR成像合成孔径等效阵元由雷达平台运动产生,只与雷达的空间采样位置有关,而与在什么时刻到达此空间采样位置无关。也就是说,SAR方位合成孔径对应的信号仅与方位采样位置有关而与采样时间无关。因此对于超大稀疏分布的小卫星SAR阵列,假设两颗小卫星星间沿航向基线为d,将其中一颗小卫星接收到的回波序列进行整数个脉冲重复时间n Tp(Tp为脉冲重复时间,n为某一正整数)的平移,等效为将原来沿航向基线缩短为d-n Tp。通过选取合适的n保证0<d-n·veqTp<veqTp,这样可以将超稀疏分布的小卫星阵列等效为基线长度不大于veqTp的小直线阵列。即使真实基线非常长,等效短阵列也不会存在包络移动问题。长阵列等效为短阵列示意图如图2所示。

图2 分布式小卫星SAR阵列等效原理示意图
经过等效相位中心处理和阵列等效后,假设“一步一停”模式,子孔径坐标系X-Y-Z下第q个等效相位中心到成像区域内某散射点l(xl,yl,zl)的斜距可以写成

式中,η=n·Tp表示方位慢时间,n表示方位采样点。分布式小卫星星座等效原点O对应的斜距为

第q个等效相位中心接收到的回波信号在解调后可以表示为

式中,σl为散射点l对应的后向散射系数;pq(·)为第q个等效相位中心发射信号形式;τ表示距离快时间;f0=c/λ为发射信号中心频率;c表示光速。对式(3)应用距离向傅里叶变换(Fourier transform,FT)可得距离波数域表达式为
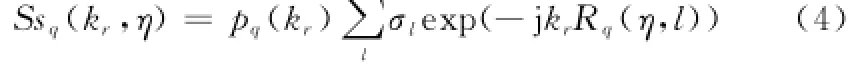
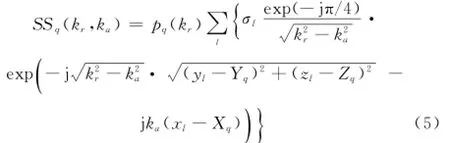
a理,由式(2)和式(5)的推导可得等效原点O对应的回波信号为
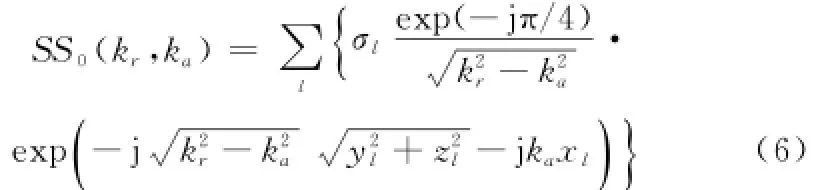
针对二维SAR成像,成像平面通常选取为沿航向方位向和垂直航向(雷达视线方向)距离向。假设成像区域内散射点高度近似相同,即设zl=h。另外可以借助数字高程图(digital elevation map,DEM)所提供的先验信息[12,20],认为h已知。再设rl表示小卫星星座等效原点O与散射点l的最近斜距,则有r为场景中心应最近斜距。如此rq可以简化为
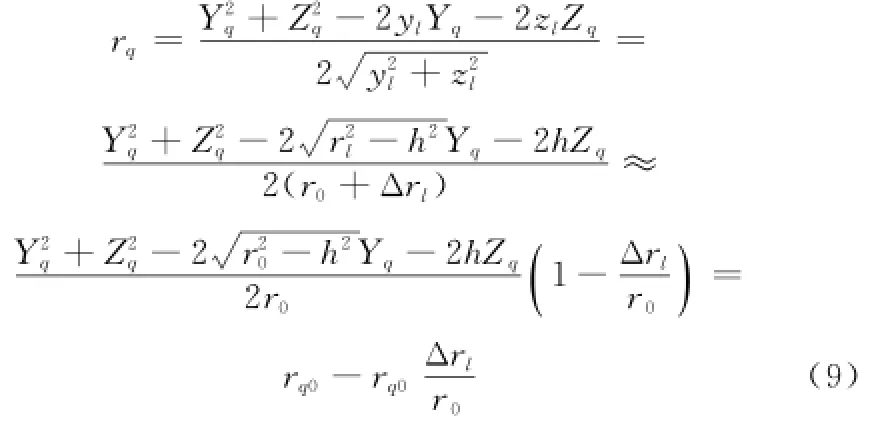
基线对应的斜距部分在Yq=0和Zq=0处进行泰勒展开
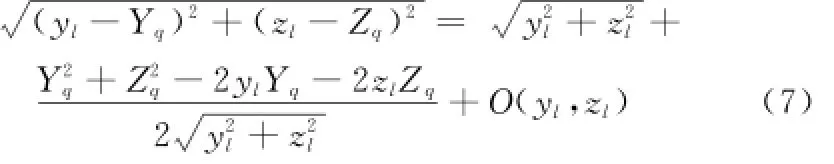
Ο(yl,zl)表示泰勒展开中的高阶项,令rq=简便起见,仅考虑单个散射点的情况,此时式(5)可以表示为
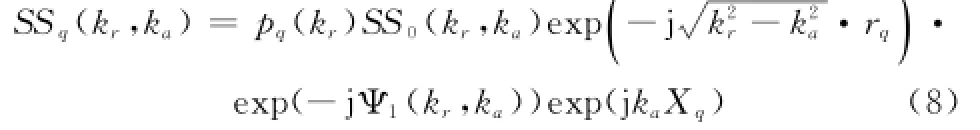
式中,Ψ1(kr,ka)=这样,分布式小卫星星座第q个等效相位中心接收到的回波表达式存在公共项SS0(kr,ka),对应的发射信号频域表示式pq(kr),垂直基线部分造成的两个相位项和水平基线部分造成的最后一个相位项。
2 垂直基线校正
式中

式中,前面一个相位项为非空变相位项,而后面一个相位项为空变相位项。为了将式(10)对应的相位在距离波数kr和方位波数ka上分离开来,可应用如下近似
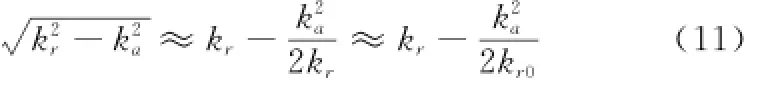
在发射信号带宽B远远小于f0时可以忽略该近似在成像中造成的误差,且表示距离波数中心。将式(11)代入式(10),可得非空变部分相位为
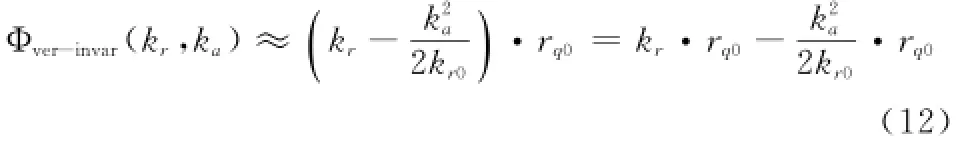
同理,式(10)中的空变相位项经过如式(11)的近似后可以写成
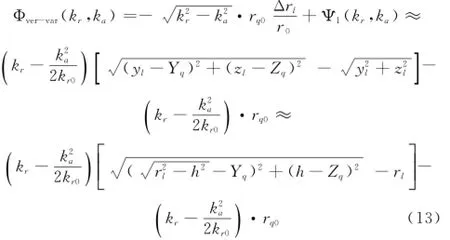
为了便于补偿该空变相位项,可以以波数中心(kr=kr0, ka=0)处计算式(13),进而补偿,则波数中心处对应的空变相位项为

依据波数中心近似的误差分析将在第3.3节进行讨论。经过以上推导,可以得到如式(12)和式(14)所示的垂直基线相位项,其中式(12)表示垂直基线对应相位的非空变部分,而式(14)则表示垂直基线对应相位的空变部分。观察式(12)可见,要补偿该相位项需要在距离波数域构造补偿函数

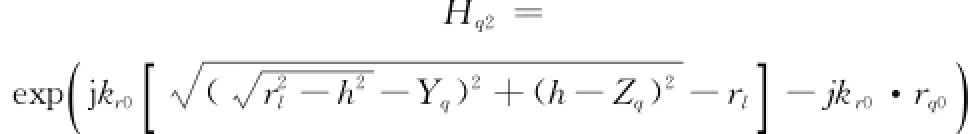
3 联合多普勒解模糊SAR成像
经过以上推导得到的非空变相位补偿公式(如式(15))和空变相位补偿公式(如式(16))进行垂直基线补偿后,分布式小卫星SAR回波信号,式(8)可以写成

利用p*q(kr)进行距离向匹配滤波,得到脉压后的回波信号为
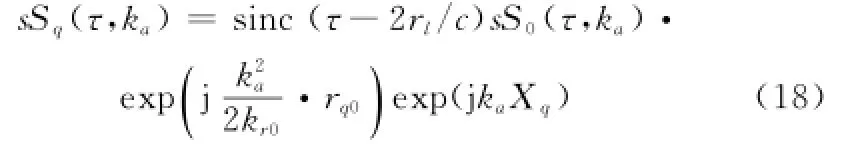
式中,第一项表示散射点距离压缩位置;第二项为各个等效相位中心接收回波的公共项;第三项为垂直基线引入的残余相位项,该项与方位波数变量相关,即与多普勒频率相关;最后一项为水平基线Xq引入的相位项,正是利用水平基线带来的方位空间自由度提供了方位空间采样,进而弥补了低方位重频造成的时间采样不足,从而为解多普勒模糊提供条件。然而,在解多普勒模糊之前,需要对剩余的垂直基线引入的相位进行补偿,现将该剩余相位表示如下

针对该相位项的补偿精度分析在后面的讨论中将详细给出。实现对该相位项的补偿操作需要在方位波数域进行,根据
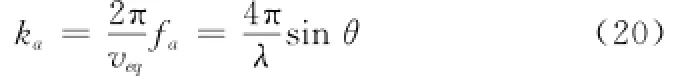
式中,θ表示方位瞬时斜视角,如图1所示。观察式(20)可见,对Φres的补偿可以在方位多普勒域进行,结合多普勒解模糊操作同样在方位多普勒域进行,可以设计在针对每一个多普勒单元进行解模糊操作前,先补偿Φres,这样可以保证解多普勒模糊精确实现。下面利用图3说明多普勒模糊的物理意义,帮助理解本文结合基线校正和解多普勒模糊操作的意义。
当方位重复频率PRF足够大于方位多普勒fa的带宽时,对应某一散射点的空时谱如图3(a)所示。此时不存在方位多普勒模糊,因为方位多普勒频率fa与方位瞬时斜视角的正弦sinθ成正比,一一对应关系。也就是说,某一方位多普勒单元fa直接对应了波束能量指向sinθ。然而,当PRF小于方位多普勒带宽时,方位多普勒谱出现混叠,对应空时谱如图3(b)所示。当方位多普勒谱存在模糊时,对于某一多普勒单元fa不再与sinθ一一对应,而是与多个sin θ对应。此时一个多普勒单元对应的能量不再来自单个波束指向θ,而是由多个指向能量混叠而成。多普勒解模糊的过程就是针对每一个多普勒单元,在多个指向θ能量混叠的情况下,逐个提取特定指向θ的能量。最后通过拼接重建不模糊的多普勒谱,如图3(a)所示。
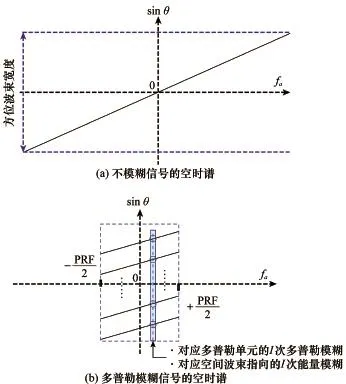
图3 方位多普勒模糊示意图
根据以上分析,多普勒解模糊算法实质上就是将对应多普勒单元fa,即对应波束指向θ,内混叠的多个多普勒频率或波束指向的能量一一提取出来,进而恢复不模糊的多普勒谱。针对某一多普勒单元进行解多普勒模糊操作前,首先补偿垂直基线剩余相位,补偿函数为

空域滤波解多普勒模糊在没有系统噪声和基线构型理想情况下可以实现性能最优,因此在算法仿真验证阶段可以借鉴使用。Capon解多普勒模糊方法具有更好的容噪性和基线误差容忍度,因此稳健性更佳,更适用于实际应用。
假设当前针对多普勒频率为fa的频点进行解模糊操作,补偿残余相位Φres后,设回波存在I次模糊(I为奇数),则各个模糊多普勒频率对应的中心为此时fa对应的各个模糊多普勒频率可以表示为考虑多普勒谱存在模糊时,第q个等效相位中心接收到的回波信号在距离多普勒域可以表示为
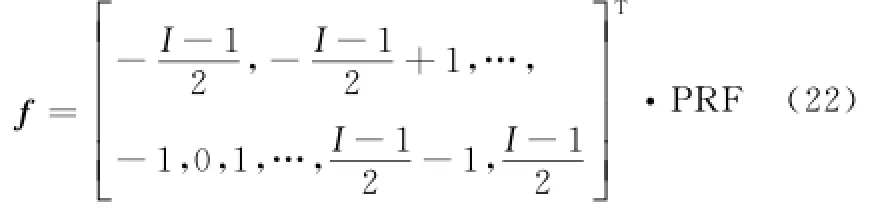

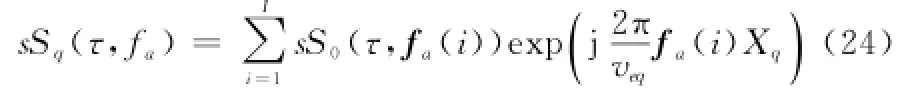
建立导向矢量矩阵为
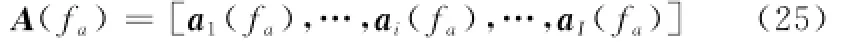
式中,针对第i个模糊分量的导向矢量为
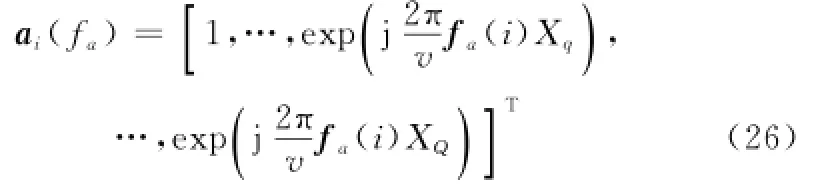
利用如式(25)建立的导向矢量矩阵,回波信号可以表示为
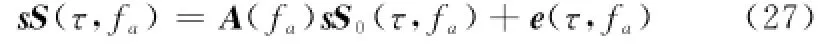
式中,e(τ,fa) 为观测噪声向量,且有
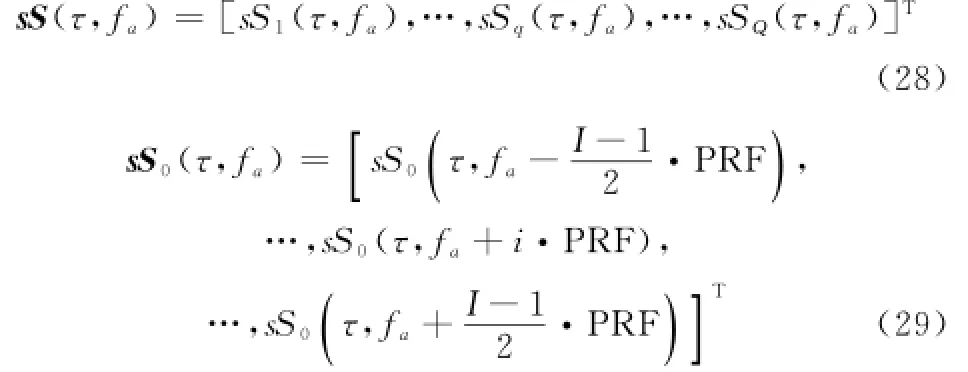
基于如上推导得到的回波信号模型,利用空域滤波和Capon谱估计方法均可实现解多普勒模糊。
3.1 空域滤波多普勒解模糊
设计空域滤波权矢量满足

式中,e(τ,fa)=wH(fa+i·PRF)·e(τ,fa)表示滤波后的噪声。非自适应权值可以表示为

式中,A+表示矩阵A的伪逆矩阵;Hi=[h1,…,hq,…, hQ]T,其中hq=i=1(波束形成条件),hq≠i=0(零点形成条件)。由此,空域滤波权矢量可以表示为

3.2 Capon多普勒解模糊
利用自适应Capon谱估计解多普勒模糊,应设计其滤波权值满足

针对第i个模糊分量的权矢量为

式中

3.3 误差分析
经过多普勒解模糊操作后,回波信号为

回波信号的二维波数域表达式符合传统SAR信号模型,即仅与散射点的位置(xl,yl,zl)有关,对上式应用传统SAR成像算法,如距离多普勒算法(range doppler algorithm, RDA)[2]、解线频调算法(chirp scaling algorithm,CSA)[3]或距离徙动算法(range migration algorithm,RMA)[3]等都可以实现对散射点的理想聚焦。
通常多普勒解模糊算法对基线精度的要求较高,尤其是非自适应的解模糊算法,要求基线精度在0.01 rad的量级,即使是对基线精度要求相对较低的自适应解模糊算法,也要保证基线精度在0.1 rad的量级。为了表明本文设计联合多普勒解模糊SAR成像对如式(19)所示残余相位Φres的补偿优越性,这里对其进行仿真比较。首先,如果不考虑残余相位Φres的补偿,针对式(12)~式(14)近似的相位差表达式为

设分布式小卫星星座由3颗小卫星组成,雷达工作在L波段,发射信号中心频率f0=1.5 GHz,带宽B=200 MHz,天线方位孔径长度Da=2 m,星座等效运行速度veq=7 200 m/s,某等效相位中心坐标(Xq,Yq,Zq)=(500 m,60 m,-60 m),某散射点(xl,yl,zl)=(0,619 km,-785 km),将如式(37)和式(38)所示的相位差绘制在距离和方位波数平面内,如图4所示。
对比图4(a)和图4(b)可见,经过残余相位补偿后,相位差由原来的1.5 rad下降到0.15 rad,提高了一个数量级,可以满足解多普勒模糊算法对基线精度的要求。

图4 波数平面相位差对比
下面分析成像场景尺寸,为了保证距离空变误差造成的越距离单元徙动小于一个距离分辨单元ρr大小的一半,即为场景中心,ρr=1 m,同样依据上面参数,r0≈1 000 km, |rq0|≈60,则|Δrl|≤8 km,即距离测绘带宽要求小于16 km。
同样对地面高程误差进行分析,设地面散射点位置为(x,y,z),而真实位置为(x,y',z+h),则高程h造成的相位差为
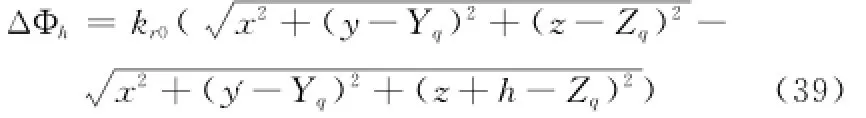
4 联合多普勒解模糊SAR成像算法流程
根据前面分析和讨论,可得本文提出的联合多普勒解模糊SAR成像算法流程如图5所示。
算法首先需要对分布式小卫星星座进行等效相位中心处理,得到对应Q颗小卫星的Q个等效相位中心,接着进行预处理简化阵列模型和轨道模型。预处理包括分布式小卫星SAR阵列等效、坐标系等效和卫星轨道曲率校正,进而将地球惯性坐标系下的曲线轨道等效为地球固定坐标系下的直线轨道。本文重点讨论分布式小卫星三维基线下多普勒解模糊SAR成像问题,因此后续分别推导得到垂直基线的非空变补偿相位和空变补偿相位。更重要的是针对垂直基线引入的残余相位,本文联合多普勒解模糊算法共同实现,如图5中虚线框所示,保证垂直基线精确补偿,进而为多普勒解模糊算法提供精度保证。
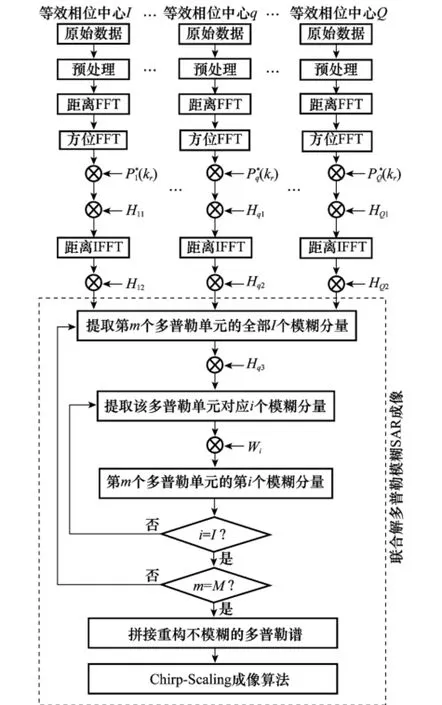
图5 联合多普勒解模糊SAR成像算法流程
5 仿真实验验证
本节针对前面推导的联合多普勒解模糊SAR成像算法进行仿真验证。仿真分布式小卫星阵列一发多收模式工作,小卫星星座由3颗小卫星组成,SAR成像系统参数如表1所示。

表1 SAR系统参数_
3颗分布式小卫星以虚拟原点O(0,0,0)为中心,分布坐标分别为(-601 m,60 m,-16 m),(1 m,-16 m,40 m)和(601 m,8 m,-36 m)。经过等效相位中心处理和SAR阵列等效后,分布式小卫星方位向分布位置为-1 m,0, 1 m。根据系统参数,方位采样间隔为veq/PRF=3 m,由此可见3个等效相位中心位置均匀分布在方位采样间隔内。因此在精确校正垂直基线的情况下,可以实现较高精度的解模糊性能。
首先针对联合多普勒解模糊SAR成像算法进行验证,设置地面散射点为3×3的矩阵,散射点分布位置示意图如图6(a)所示,其中距离向间隔为6.5 km,方位向间隔为1 km,另外标号场景中心散射点为O和场景边缘某一散射点为A。根据表1所示系统参数,方位多普勒带宽为2veq/ Da=7 200 Hz,然而系统方位向采样重复频率PRF仅为2 400 Hz,因此必然存在多普勒模糊,模糊倍数为3倍。在多普勒存在模糊情况下,并且未对多普勒进行解模糊,得到的SAR成像结果如图6(b)所示。应用本文设计联合多普勒解模糊SAR成像算法(算法流程见图5)得到的结果如图6(c)所示。通过对比可见,经过联合多普勒解模糊SAR成像算法后,散射点的方位模糊现象明显消除,散射点被聚焦在固定位置。

图6 联合多普勒解模糊SAR成像散射点仿真实验
下面分析联合多普勒解模糊算法性能。图7(a)和图7(b)分别给出多普勒解模糊前后散射点A所在距离分辨单元对应的方位幅度响应。对比可见,没有进行多普勒解模糊得到的响应,模糊信号能量较高,进而造成模糊点。而经过联合多普勒解模糊SAR成像后,得到的响应图模糊信号被大大抑制,模糊能量被压制在-50 dB以下。
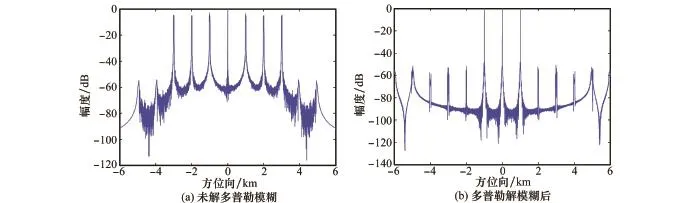
图7 散射点方位响应对比
接下来,给出联合多普勒解模糊SAR成像算法聚集性能。如图8所示分别为散射点O和散射点A对应的二维响应等高图,同时给出对应距离向和方位向的分辨率,峰值旁瓣比(PSLR),积分旁瓣比(ISLR)。由实验数据可知,联合多普勒解模糊SAR成像算法聚焦性能达到成像要求。
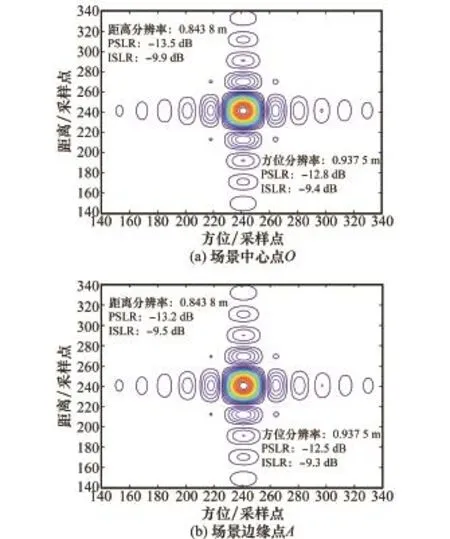
图8 散射点响应等高图及性能参数
最后,考虑实际星载SAR空地关系,采用CARTWHEEL构形编队[13]一发三收工作模式的轨道根数进行仿真验证。仿真中,主星雷达以正侧视工作,3颗卫星的轨道参数如表2所示,雷达系统参数如表3所示。经过本文所提分布式小卫星联合多普勒解模糊SAR成像算法后,可得成像结果如图9所示,其中散射点的位置设置与上面实验相同。

表2 3星编队轨道根数

表3 雷达参数_

图9 CARTWHEEL构形编队仿真结果
6 结 论
本文针对分布式小卫星SAR成像问题提出联合多普勒解模糊SAR成像算法,实现低方位重频采样条件下的高分辨宽测绘带SAR成像。该算法可以有效校正分布式小卫星三维基线构型下的垂直基线,包括非空变部分和空变部分。同时结合多普勒解模糊算法实现对残余垂直基线相位项的精确校正,保证后续多普勒解模糊算法的精确实现。另外,针对SAR阵列等效、基线校正精度以及误差分析进行讨论,方便本文所提联合多普勒解模糊算法的工程应用。最后利用仿真实验数据验证该算法的有效性。
[1]Krieger G,Fiedler H,Zink M,et.al.The TanDEM-X mission:a satellite formation for high-resolution SAR interferometry[J].IEEE Trans.on Geoscience and Remote Sensing,2007,45(11),3317-3341.
[2]Ian G C,Frank H W.Digital processing of synthetic aperture radar date:algorithms and implementation[M].Beijing:Publishing House of Electronics Industry,2007.
[3]Bao Z,Xing M D,Wang T.Radar imaging technology[M]. Beijing:Publishing House of Electronics Industry,2005.
[4]Qi W K,Yu W D,Huang P P.Moving target acceleration indication and estimation for space-borne bistatic synthetic aperture radar[J].Systems Engineering and Electronics,2010,32(5): 946-950.(齐维孔,禹卫东,黄平平.星载双站SAR运动目标加速度检测和估计[J].系统工程与电子技术,2010,32(5):946 -950.)
[5]Helko B,Thomas F,Marie L,et al.TerraSAR-X processing and products[J].IEEE Trans.on Geoscience and Remote Sensing,2010,48(2):727 740.
[6]Krieger G,Gebert N,Moreira A.Multi dimensional waveform encoding:a new digital beamforming technique for synthetic aperture radar remote sensing[J].IEEE Trans.on Geoscience and Remote Sensing,2008,46(1):31-46.
[7]Zan F D,Monti G A.TOPSAR:terrain observation by progressive scans[J].IEEE Trans.on Geoscience and Remote Sensing, 2006,44(9):2352 2360.
[8]Callaghan G D,Longstaff I D.Wide-swath space-borne SAR using a quad-element array[J]∥Proc.of the Institution Electrical Engineer,Radar Sonar and Navigation,1999.
[9]Cantafio L J.Space-based radar handbook[M].Boston:Artech House,1989.
[10]Xu W,Deng Y.Multi-channel SAR with reflector antenna for high-resolution wide-swath imaging[J].IEEE Antennas and Wireless Propagation Letters,2010,9:1123-1126.
[11]Li Z F,Wang H Y,Bao Z.Generation of wide-swath and highresolution SAR images from multichannel small spaceborne SAR system[J].IEEE Geoscience and Remote Sensing Letters, 2005,2(1):82-86.
[12]Li Z F.SAR-InSAR-GMTI processing for distributed small satellites[D].Xi’an:Xidian University,2006.(李真芳.分布式小卫星SAR-InSAR-GMTI的处理方法[D].西安:西安电子科技大学,2006.)
[13]Massonnet D.Capabilities and limitations of the interferometric Cartwheel[J].IEEE Trans.on Geoscience and Remote Sensing, 2001,39(3):506-520.
[14]Xing M D,Li Z F,Bao Z,et al.Study of distuibuted microsatellites radar space-time-frequency imaging method[J].Journal of Astronautics,2005,26(z1):70-82.(邢孟道,李真芳,保铮,等.分布式小卫星雷达空时频成像方法研究[J],宇航学报, 2005,26(z1):70-82.)
[15]Li Z F,Xing M D,Wang T,et al.Distributed small satellites SAR signal processing for achieving full azimuth resolution[J]. Acta Electronlc Sinica,2003,31(12):1800-1803.
[16]Li J,Stoica P,Wang Z.On robust capon beamforming and diagonal loading[J].IEEE Trans.on Signal Processing,2003, 51(7),1702 1715.
[17]Li J,Stoica P,Wang Z.Doubly constrained robust Capon beamformer[J].IEEE Trans.on Signal Processing,2004,52 (9):2407-2423.
[18]Yang L,Zhang L,Tang Y,et al.Doppler ambiguity suppression SAR imaging using distributed micro satellites[J].Journal of Electronics and Information Technology,2011,33(2):355 -362.(杨磊,张磊,唐禹,等.分布式小卫星SAR多普勒解模糊SAR成像[J].电子与信息学报,2011,33(2):355-362.)
[19]D’Aria D,Guarnieri A M,Rocca F.Focusing bistatic synthetic aperture radar using dip move out[J].IEEE Trans.Geoscience and Remote Sensing,2004,42(7):1362-1376.
[20]Sheng Y,Alsdorf D E.Automated georeferenceing and orthorectification of Amazon Basin-wide SAR mosaics using STRM DEM data[J].IEEE Trans.Geoscience and Remote Sensing, 2005,43(8):1929-1940.
Joint Doppler ambiguity removal SAR imaging algorithm for distributed micro-satellite
ZHANG Long1,2,SU Tao1,LIU Zheng1,HE Xiao-hui1,2
(1.National Lab of Radar Signal Processing,Xidian University,Xi’an 710071,China; 2.College of Electronics and Information,Xi’an Polytechnic University,Xi’an 710048,China)
A joint SAR imaging algorithm with Doppler ambiguity removal is proposed,which can be used for high resolution wide swath SAR imaging in low pulse repetition frequency(PRF)for distributed micro-satellite constellation.The algorithm is capable of correcting the vertical baseline effectively,not only for the rangeinvariant component and range-variant component,but also for the phase related to residual baseline in vertical combined with Doppler ambiguity removal.Consequently,the Doppler ambiguity can be removed as completely as possible.Moreover,the algorithm precision is also analyzed to support its potential in real application.Finally,simulated data experiment is designed to validate the proposal.
distributed micro-satellite;synthetic aperture radar(SAR);baseline correction;Doppler ambiguity removal
文献标志码:A DOI:10.3969/j.issn.1001-506X.2015.03.11
张 龙(1975-),男,副教授,博士后,主要研究方向为信号处理与雷达成像。
E-mail:zhanglong@mail.xidian.edu.cn
苏 涛(1968-),男,教授,博士,主要研究方向为面向雷达、声纳、通信的高速实时信号处理信号处理快速算法研究、并行处理系统设计。E-mail:sutao@xidian.edu.cn
刘 峥(1964-),男,教授,博士,主要研究方向为多源协同探测与信息融合、智能雷达探测系统。
E-mail:lz@xidian.edu.cn
贺小慧(1981-),女,讲师,主要研究方向为智能信号处理。
E-mail:Hexiaohui6666@163.com
网址:www.sys-ele.com
1001-506X(2015)03-0544-09
2014- 01-11;
2014- 10-28;网络优先出版日期:2014- 11-03。
网络优先出版地址:http://w ww.cnki.net/kcms/detail/11.2422.TN.20141103.1613.002.html
国家部委预研基金项目(9140A07030211DZ0113);中国博士后科学基金面上项目(2013 M542329);陕西省自然科学基础研究计划项目(2012JM8015);陕西省教育厅专项计划项目(12JK0530,12JK0557)资助课题

