永定河泛区洪水调度数值模拟

李大鸣，王 笑，赵明雨，张建中，刘思清，刘江侠

永定河泛区洪水调度数值模拟

李大鸣1，王 笑1，赵明雨1，张建中2，刘思清2，刘江侠2

(1. 水利工程仿真与安全国家重点实验室(天津大学)，天津300072；2. 水利部海河水利委员会科技咨询中心，天津 300170)

提出了具有旁侧出流的河网独立计算的一、二维多口门嵌套衔接模式，建立了一维河道嵌套于平面二维永定河泛区洪水演进水流数学模型．结合历史调查洪水资料对永定河泛区洪水演进进行了模型验证，二者结果基本吻合．应用该模型对永定河泛区洪水调度方案进行了模拟，先后模拟了无机场、机场近期建设后和远期建设后3种工况下的洪水演进过程．分析对比机场建设前后各分洪区洪水位、滞洪量、淹没范围的变化．模拟结果显示，各分洪口门启用时间稍微提前，机场建设区寺垡辛庄口门启用次序稍有变化，水位的雍高、分洪量的增量、淹没范围的变化对泛区洪水调度方案影响较小，表明了机场建设的可行性．该研究为淹没区的洪灾损失评估及相应的防洪调度方案修订提供了必要的参数和依据．

永定河泛区；洪水演进；一、二维衔接模型；有限体积法

20世纪80年代以来，洪水灾害越来越频繁，受灾面积和经济损失也越来越严重，洪水演进数值模拟作为非工程措施的重要组成部分，是模拟和掌握洪水演进规律的重要方法之一，可为区域洪水风险图制作、洪水预警预报、寻找最佳调度方案等提供重要依据[1-2]．

研究洪水在河道、分蓄洪区的演进过程是一项重要而复杂的工作，一维河道模型能从整体上模拟各河道断面水力要素(流量、水位等)随时间变化过程，对于分蓄洪区洪水演进，则需要在平面二维洪水演进模拟的基础上，掌握分洪区洪水淹没历时、淹没深度、流场分布等情况，才能制定相应的分洪调度方案．对于洪水演进数值模拟，国内外很多学者都进行了研究，如意大利的Caleffi等[3]采用二维浅水方程对Toce河的洪水演进进行了模拟；Garcia等[4]建立有限差分法模型，较好地处理了非线性项的问题；我国梅亚东等[5]、谢作涛等[6]采用Preissmann 4点偏心隐格式建立了一维洪水演进数学模型；谭维炎等[7]提出了计算二维浅水运动的一种高性能格式和二阶高性能算法，对长江中游洞庭湖水流的数值模拟取得了很好的效果；王船海等[8]将一维、二维模型相结合，采用直角坐标下非均匀矩形网格的控制体积法模拟流域洪水；李云等[9]采用剖开算子法建立了一、二维洪水演进嵌套数学模型，应用于淮河临淮岗洪水控制工程；李大鸣等[10]采用有限体积法建立了适用于河道、滞洪区复杂情况的洪水演进一、二维衔接数学模型；杨芳丽等[11]采用Preissmann 4点偏心隐格式和有限体积法分别对一、二维河网进行离散，对长江干流螺山-汉口河段和汉江支流东荆河水系分蓄洪区调度方案进行了模拟．

河道、滞洪区洪水演进计算的难点在于对洪水运动的连续过程和多方向洪水遭遇所产生的相互影响进行研究．笔者针对滞洪区的复杂地形和多个分洪口门的情况，采用有限体积法建立一维河道嵌套于平面二维洪水演进模型，把一、二维河道同二维滞洪区衔接起来，从而可以根据不同的洪水情况，更合理地选择防洪调度方案，准确、及时地调控滞洪区各口门的启用，减少洪灾损失．

1 数学模型理论

1.1 一维河道模型

1.1.1 一维非恒定流基本方程连续方程

运动方程

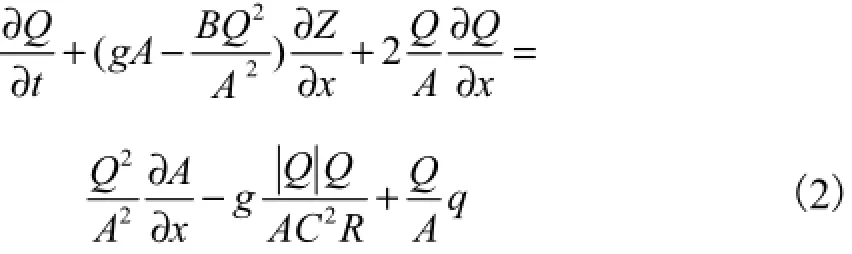
式中：Z为水深；t为时间坐标；B为模化宽度；Q为流量；x为沿程断面坐标；q为旁侧出流单宽流量；g为重力加速度；A为计算断面的过水面积；C为谢才系数；R为水力半径．

1.1.2 求解方法

采用3点隐式差分格式对式(1)和式(2)进行离散，这种方法计算简单，并且具有较好的稳定性，水位、流量位置如图1所示，选择跳点格式安排水位和流量断面，水位安排在格点断面，流量安排在分点断面上，用下标表示空间断面位置.

图1 水位、流量位置示意Fig.1 Schematic diagram of water level and flow rate

离散方程为

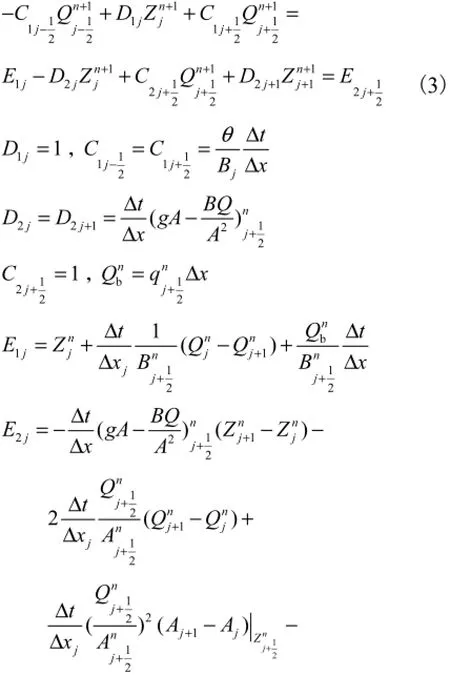
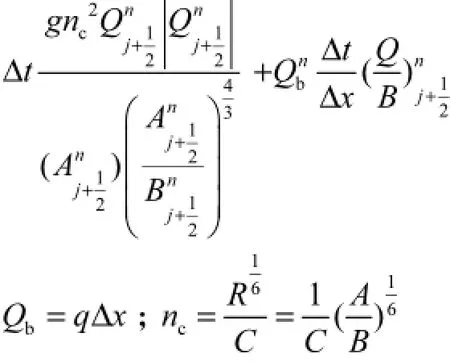
式中：θ为权重系数；xΔ为断面间距；tΔ为时间步长．

通过方程离散，求解非线性偏微分方程式(1)和式(2)，转化为求解差分方程式(3)．假设河道有m个水位点断面，相应有1m-个流量点断面，依据式(3)从1到m排列这些方程，并以矩阵形式表示为

其中

综上所述，演算明渠非恒定流的问题，需要在边界条件或者上下游的约束条件已知的情况下，按照追赶方程组先求出各个追赶系数，再将追赶系数代回方程组，即可求得各个断面的流量或水位，即方程得解.

1.2 平面二维洪水演进模型

1.2.1 二维非恒定流基本方程连续方程

动量方程

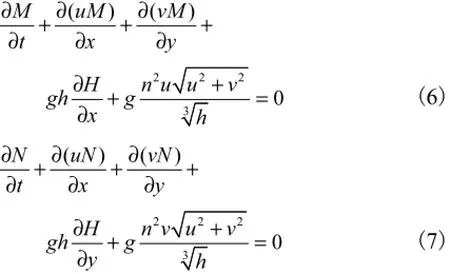
式中：H为水位；Z=Z0+H，Z0为底高程；M、N分别为x、y方向上的单宽流量，M=Hu，N=Hv；u、v分别为x、y方向的平均流速；n为糙率．

1.2.2 求解方法

为了更好地适应永定河泛区的复杂边界，按照有限体积法思想，采用无结构不规则网格布置方式，如图2所示，单元网格为控制体，在网格中心处计算水位H，在网格周边通道的中点处计算流量Q．在平衡计算时，沿控制体每一边的法向通量用该边中点处的通量作代表，乘以边长即为通量沿该边的积分．中点的通量可用中心格式(如取相邻两格子形心处通量的平均)或逆风格式确定．将式(5)改写成矢量形式，按照有限体积法，将其在控制体内进行积分，对水位H和流量Q按时间交错方式进行计算(如图3所示)，则

图2 水位H和流量Q的空间布置方式Fig.2Space arrangement plan of water level H and flow rate Q

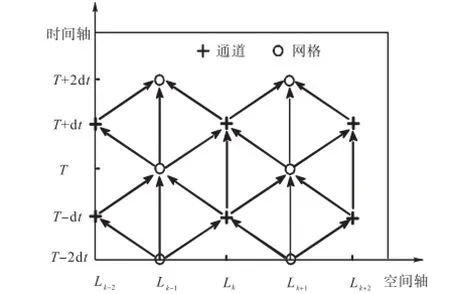
图3 水位H和流量Q的时间交错计算方式Fig.3Time arrangement plan of water level H and flow rate Q

式(5)可离散为

式中：iA为第i个网格的单元面积；ikL为i号网格的第k号通道的长度；ikQ为i号网格的第k号通道的单宽流量；iq为第i个网格的抽排水量；T为起算时刻；K为通道总数．

1.3 一二维模型衔接方式

蓄滞洪区和河道是通过分洪口门联结在一起的，一二维模型衔接模式采用一维旁侧出流流量等于二维模型边界流量、一二维水位差确定堰流流量和方向的方法交替叠代计算，达到一二维衔接模型联解的目的．衔接口门计算条件为

式中：jQ为一维旁侧出流流量；QΓ为二维模型边界流量；jH为衔接断面上游的堰上水头；ε为侧收缩系数；sσ为淹没系数．

为提高计算精度，对一维河道进行独立求解，通过河道旁侧出流条件为二维泛区模型提供入流条件，并考虑各分区之间水体交换过程及淹没情况，为评估分洪区内经济损失提供依据．其中河道旁侧出流由分洪口门进洪条件控制，当河道中水位超过对应口门分洪水位时，洪水由河道进入泛区，分洪控制区域开始启用；当泛区内水位升高超过河道水位及对应口门的底坎高程时，水流自泛区回流入河道．这一功能在洪水退水时表现得尤为明显和有效．

采用一维河道嵌套平面二维洪水演进模型稳定性好，能实现一、二维模型的真正耦合，可在一维、二维模型的交界面(比如蓄滞洪区口门)实时交换动态信息[12]．

2 洪水演进数学模型的建立

永定河泛区中低标准洪水以河道行洪为主，本文数学模型依据2003年实测1∶10,000比例尺地形图和河道纵横断面图等最新的地形地貌和工程资料，建立了一、二维嵌套水力学模型．

2.1 永定河泛区基本情况

现今的永定河泛区是在1939年洪水永定河改道后形成的，上自梁各庄，下至屈家店，承担“缓洪、沉沙、削峰”任务．泛区内历史形成了多道小埝，分别为北小埝、南小埝、北前卫埝、南前卫埝、北围埝和南围埝，将泛区分隔成4个区域共计9个部分．考虑泛区的分区运用，各小埝上共计规划安排了6个固定分洪口门．包括北围埝上的茨平口门、北前卫埝上的西孟村口门、南前卫埝上的池口口门、南小埝上的南石口门和潘庄子口门、北小埝上的王码口门，另外设有寺垡辛庄口门．各分区控制口门位置及选取的典型水位点如图4所示．

图4 分洪口门位置示意Fig.4 Schematic diagram of flood diversion entrance location

现行的《永定河洪水调度方案》(2004年)中，泛区各小埝分洪口门分洪运用条件由《永定河卢沟桥以下中小洪水调度方案》规定的卢沟桥处的流量控制，改为分洪口门前水位控制，各埝分洪口门设计进洪水位及对应的卢沟桥下泄流量见表1．

2.2 计算范围及模型结构

现有地形资料表明，西张务以及下游河道防洪能力偏低，当行洪流量大于500,m3/s时，洪水将无法顺畅下泄，洪水将出槽形成漫流，严格上讲水流已具有二维性质，所以一维河道模型截取原河道的上游河道105个断面，在西张务处与二维泛区河道衔接．一维河道还包括池口分洪后在南前卫埝与南小埝间的19个断面，从池口分洪口门到南石口门上游和朱庄至西张务之间的堤外断面共13个．一维河道入流边界为永定河上游来水边界(永定河泛区进口梁各庄上游断面的洪水过程线)如图5所示(横坐标中“时间”是指洪水行洪时间)，出流边界为西张务断面水位流量关系如图6所示．

表1 永定河泛区各分洪口门控制参数Tab.1 Control parameters of each flood diversion entrance in the Yongding River flood detention basin

图5 永定河泛区进口梁各庄上游断面的洪水过程线Fig.5 Flood hydrograph of Lianggezhuang village upstream section in the detention basins of Yongding river

图6 西张务断面水位流量关系Fig.6 Relationship between water level and flow rate ofXizhangwu section

河道与二维泛区衔接断面有池口口门、寺垡辛庄口门、王玛口门、南石口门、西孟村口门、茨平口门、朱庄前卫埝．潘庄口门在一维河道和二维泛区中都有衔接计算，通过一维、二维结果互相验证．运用一二维模型衔接条件对其他各控制口门流量进行计算．

二维泛区剖分为9,687个结点、8,549个单元和18,234个通道，包括老米店、黄花店、安次和永清4个安全区，5个主要滞洪区分区使用．二维模型中潘庄子口门控制南小埝两侧的衔接，龙河扒口门连通龙河两侧的滞洪区．该模型的入流边界为西张务水位流量关系，出流边界为屈家店断面水位流量关系，如图7所示．

图7 屈家店断面水位流量关系Fig.7Relationship between water level and flow rate of Qujiadian section

2.3 网格划分

本次网格剖分的最大特点是把河道和滞洪区分开单独进行网格划分，这样就可根据不同的洪水情况，如在来水较少的情况下，单独对河道进行行洪控制．而遇到汛期较大洪水的情况下，由于河道蓄满，为保证下游河道和城市的安全，需要运用到滞洪区分洪、滞洪的时候，可以把一、二维河道同二维泛区衔接起来进行洪水演进计算，这样就形成了河道型网格嵌于地面型网格之上紧密相连的一二维衔接模型网格，如图8所示．

2.4 糙率系数

糙率是反映河道边界粗糙情况、河道形态等所有影响水流阻力因素的综合参数，泛区糙率取值见表2，河道糙率主槽选取为0.025，边滩糙率选取为0.06，糙率n处理方法[13]有以下3种．

图8 一二维衔接模型网格Fig.8 Grids of one-dimensional and two-dimensional linkup model

(1) 姜国干剪切力叠加法

(2) 爱因斯坦等流速法

(3) 洛特尔流速关系法

式中：zn是主槽糙率；bn是边滩糙率；χ是断面湿周；zχ是主槽湿周；bχ是边滩湿周；R是断面水力半径；zR是主槽水力半径；bR是边滩水力半径．

本模型选取爱因斯坦等流速法计算综合糙率.

表2 一二维衔接模型糙率取值Tab.2 Roughness values of one-dimensional and twodimensional linkup model

3 模型验证

采用现有的1956年较大洪水在永定河泛区的演进情况对模型进行验证．泛区中7个位置处的水位对比如表3所示．由计算结果可以看出，数值计算得到的水位偏低，这是由于屈家店枢纽于1969年建成了永定新河闸，改变了枢纽的水位流量关系，从而导致蓄滞洪区中的洪水自河道下泄较多，泛区内计算水位偏低，这与表3中情况基本相符．洪水调查报告显示，洪水进入泛区后，“大北市”首先决口，随后“琥珀营”与“柳园”决口，在洪水进入泛区后的第8个小时“姜志营”村东北角决口，所以从洪水传播的速度与方向来看，各口门决口时间、决口顺序也是比较合理的．如表4所示，相比于近100,h的总行洪时间，误差均在可接受范围内．因此模型具有较高的可信度，可以用于预测、模拟不同来水情况下永定河蓄滞洪区内洪水的演进情况．

表3 1956年特征点水位计算结果对比Tab.3Comparison of water level at characteristic spot between the calculated and the measured in 1956

表4 泛区计算与调查的洪水演进过程对比Tab.4Comparison of flood routing between the calculated and the measured in flood detention basin

4 机场建设前后泛区洪水数值模拟分析

为保障机场的安全，需在机场外围修建防洪堤，这样机场近期建设之后占据的蓄滞洪区面积将达到23.55,km2，占寺垡辛庄分洪区面积的67%，远期建设之后占据的蓄滞洪区面积将达到30.95,km2，占寺垡辛庄分洪区面积的85%．由此可见，机场远期建设后其占据蓄滞洪区的面积很大，且排水规模将增加到100,m3/s，将给永定河系防洪带来一定的不利影响．针对其对永定河防洪的影响程度，对机场近期、远期建设(两种工况分别对应于45,m3/s方案、100,m3/s方案)后的洪水进行模拟计算．

4.1 机场建设前洪水演进过程

在目前现状防洪工程条件下，采用一二维嵌套数学模型，按照500,m3/s、800,m3/s、1,000,m3/s、1,500 m3/s 4个洪峰流量标准，以及10年一遇、20年一遇、50年一遇、100年一遇、200年一遇5种频率的典型标准洪水进行了模拟分析．由于篇幅有限，本文仅选取了具有代表性的流量过程，下面以机场建设前100年一遇洪水为例，展示泛区洪水演进过程，如图9所示．

在一维河道入流后，首先在西张务断面(原河道上游第105个断面)与二维泛区衔接，二维泛区从无水干河床起算，随时间发展，河道洪水向下游演进，西张务以下窄河段处左右堤约在行洪时间27,h时破堤分洪，窄河段堤防溃决；遭遇100年一遇洪水时在28.25,h，茨平口门首先达到最高水位15.419,m；然后，朱村水位达到围埝顶高程，在朱村至西张务间前卫埝以西过流，龙河右岸水位达到分洪水位．在55.88,h，西孟村口门达到最高水位16.700,m；在351.48,h，池口口门最高水位为22.080,m；在55.87,h，南石口门达到最高水位17.830,m，河道洪水向各区分洪．在334～335,h，天堂河旁的河道水位超寺垡辛庄口门分洪水位，开始向永定河左岸、天堂河右岸高地的寺垡辛庄分洪区分洪．在339～340,h之间，潘庄子口门启用，王玛口门随即打开，至此泛区全面启用．至700,h左右，淹没范围大幅减小．王玛分洪区洪水经西孟村分洪区、茨平分洪区向龙河分洪口附近退水；潘庄子分洪区经南石分洪区、朱庄-西张务附近断面汇流至河道，并与二维模型衔接，与茨平分洪区洪水汇合后，向屈家店闸汇流．

4.2 机场建设后洪水数值模拟及对比分析

4.2.1 口门启用次序、时间变化

表5给出了不同工况下各进洪口门分洪时刻．目前工程条件下，各口门扒口顺序依次为茨平、西孟村、池口、南石、潘庄子、王玛．寺垡辛庄口门使用次序排在南石口门之后，启用流量在800,m3/s以上．在机场近期建成之后和远期建设之后两种工况下，由于寺垡辛庄口门距离机场排水点较近，机场排水对该口门的使用次序产生一定影响．800,m3/s以下典型洪水过程中，现状条件下寺垡辛庄口门尚未使用，加入机场排水后该口门即开始使用，且使用次序提前到南石口门分洪之前．1,000,m3/s以上典型洪水过程，寺垡辛庄分洪口门的使用次序在南石口门分洪之后，与现状工程条件分洪次序一致．

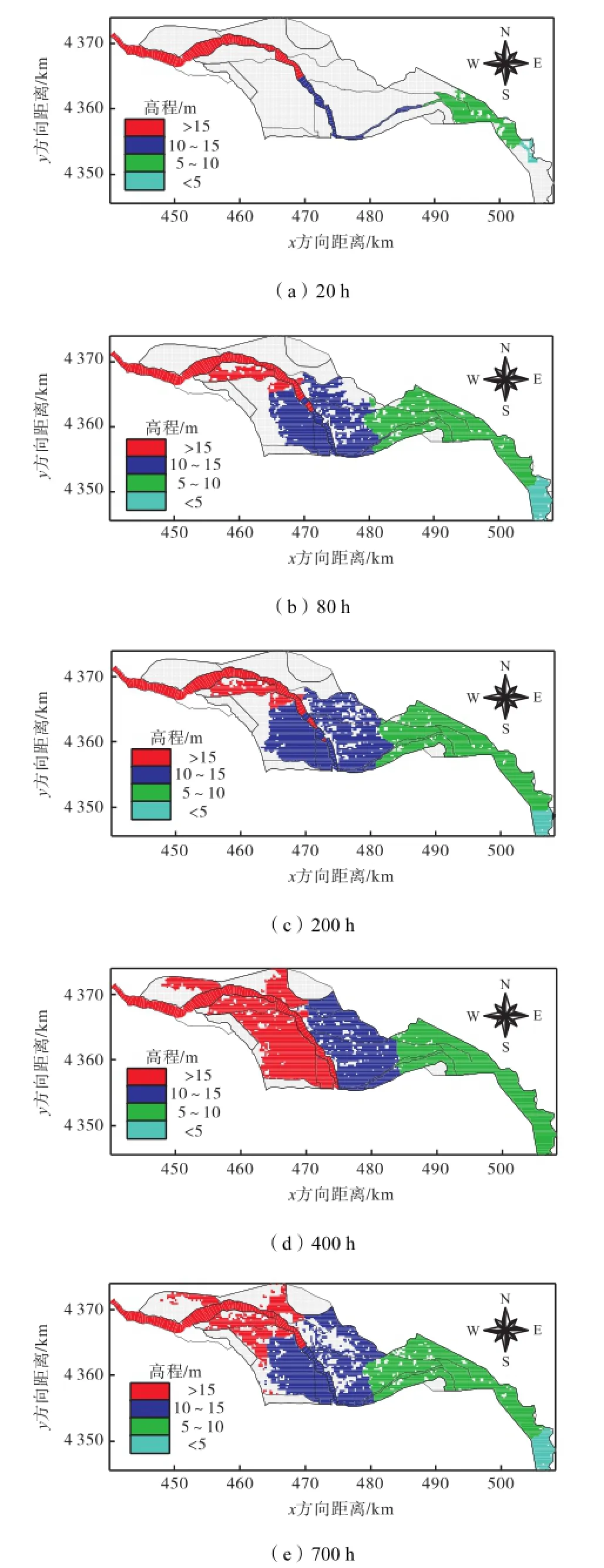
图9 一二维衔接模型100年一遇无机场洪水演进Fig.9Flood routing process at one percent flood frequency for one-dimensional and two-dimensional linkup model before the construction of airport

分别就各洪峰流量标准的洪水过程，模拟分析机场近、远期建设完成后各进洪口门相对无机场的分洪运用情况．由表5可知，机场场区排水造成沥水流量增加，小洪水时各口门的分洪时间有所提前，大洪水时茨坪、西孟村、池口和南石口门的分洪时间基本不受影响．按照洪水过程洪峰与沥水过程洪峰这一峰峰对应的不利组合考虑，各口门分洪时间提前时间在2,h以内．

表5 不同工况下各进洪口门分洪时刻Tab.5 Flood diversion time of each flood diversion entrance under different working conditions

4.2.2 口门水位雍高

机场建设除了对天堂河口旁的寺垡辛庄口门的调度有较大影响外，对其他6个口门的中小洪水调度影响不大．机场建设前后各控制口门流量和河道水位如表6所示．其中只要茨平、西孟村、池口、南石4个口门启用实施分洪，在机场近期“45,m3/s方案”中，河道水位的雍高仅在0.001～0.002,m，分洪增量在0.194～5.704,m3/s；在机场远期“100,m3/s方案”中，分洪水位的雍高仅在0.004～0.030,m，分洪增量在1.316～11.752,m3/s；对于没有达到分洪水位或没有实施分洪的两个口门——潘庄子口门和王玛口门，影响的水位高度约0.021～0.110,m，影响后的最高水位仍然低于100年一遇设计洪水位；对于寺垡辛庄分洪口门，因其处于天堂河口溢流口门附近，使溢流口门的溢流时间提前，水位加高，溢流分洪量也增加．中小洪水情况下，口门前水位雍高不大；遇200年一遇设计标准洪水，口门水位分别达到最大雍高0.054,m、0.291,m，分洪流量分别增加12.098,m3/s、22.744,m3/s．

4.2.3 区域内水位雍高

表7给出了不同工况下各分洪区最高水位及最大雍高．各口门在不同流量下启用，且机场建设前后启用时间不同，但泛区经历20年一遇以上洪水时，所有口门都已经打开，此后各分洪区域均已启用．相对于机场建设前，机场近期远期建设后区域内的水位均有变化．各区域内最高水位均发生在200年一遇洪水的情况下，最大雍高大部分发生在50年一遇和100年一遇的情况，且远期比近期“45,m3/s方案”雍高大1倍多．

受机场建设影响最大的区域在天堂河口旁高地上位置，即寺垡辛庄分洪区机场占用后剩余的部分区域．这里靠近天堂河口，受天堂河入流量和机场排沥的影响，也受滞洪区范围变小因素的影响，使区域水位受到的影响比较大，机场建设前最高水位为22.396,m，机场近期“45,m3/s方案”和机场远期建设两种情况下，最高水位分别为22.500,m、22.753,m，发生于200年一遇洪水．两种情况下最大雍高分别为0.156,m、0.425,m，发生于50年一遇洪水．100年一遇洪水不同工况下泛区淹没水深等值线图见图10～12．

表6 不同工况下各口门流量和河道水位Tab.6 Entrance flow rate and river water level under different working conditions

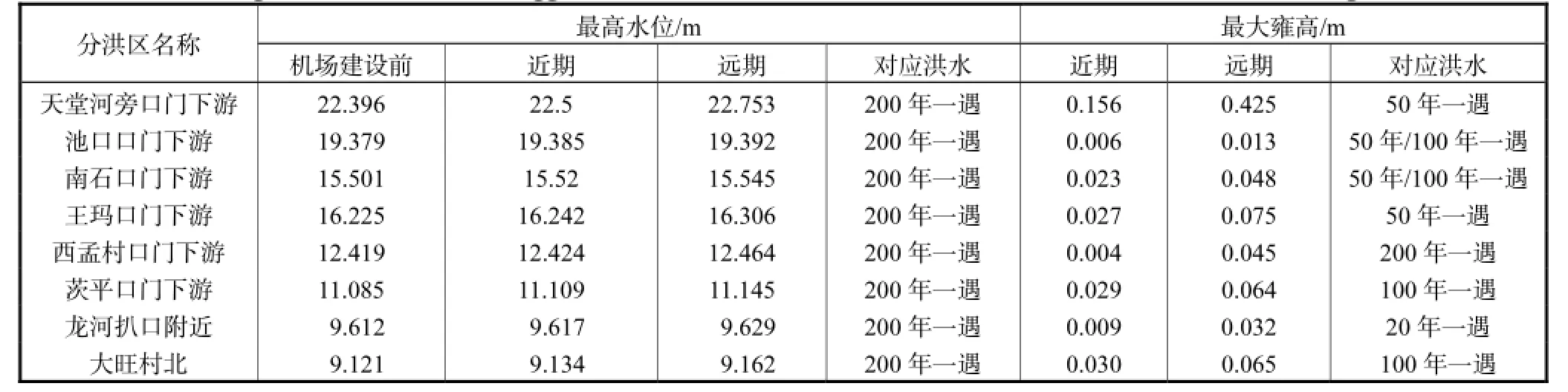
表7 不同工况下各分洪区最高水位及最大雍高Tab.7 The highest water level and biggest fluctuation of each flood diversion area under different working conditions

图10 100年一遇无机场淹没水深等值线图Fig.10 Contour map of the submerged depth at one percent flood frequency before the construction of the airport

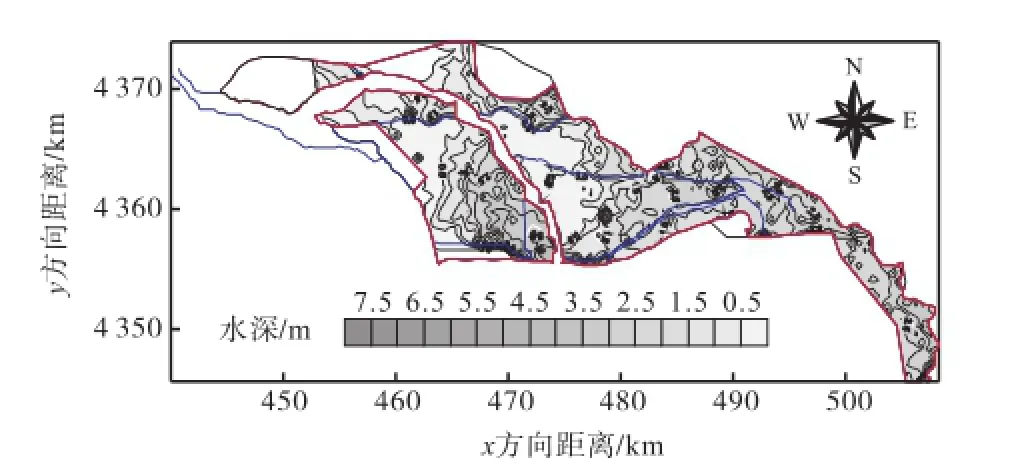
图11100 年一遇机场近期45,m3/s方案淹没水深等值线图Fig.11Contour map of submerged depth at one percent flood frequency under the recent 45,m3/s construction project

4.2.4 淹没范围扩大

对比有机场和无机场泛区的淹没情况时，将永定河泛区分成寺垡辛庄分洪区与寺垡辛庄以外的泛区两片分别进行比较．

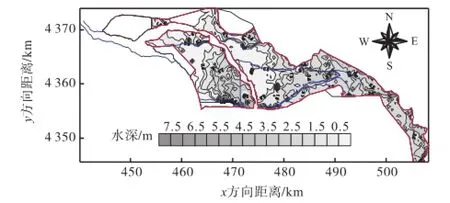
图12 100年一遇机场远期100,m3/s方案淹没水深等值线图Fig.12 Contour map of submerged depth at one percent flood frequency under the long-term 100,m3/s construction project

河道入流为500,m3/s时，寺垡辛庄分洪区没有启用，故该分洪区有无机场均没有淹没；而寺垡辛庄之外的泛区，因机场排水流量的增加，淹没面积逐渐增加．河道入流为800,m3/s时，无机场排水情况下，寺垡辛庄分洪区没有启用，机场建成后，增加了机场排水，其淹没面积也逐渐增加，而寺垡辛庄之外的泛区，因机场排水流量的增加，淹没面积逐渐增加．河道入流为1,000,m3/s时，整个永定河泛区淹没面积都随着机场排水而增加．河道入流为1,500,m3/s时，在机场近期“45,m3/s方案”下寺垡辛庄淹没面积增加0.49,km2，远期建设情况下淹没面积减少了0.38,km2；而泛区其他区域的淹没面积是增加的，但是增量开始减小．中小洪水情况下各方案最大淹没面积如表8所示．

设计标准洪水，即永定河100年一遇洪水条件下，泛区以上河道入流2,500,m3/s，无机场占压和排水情况下，寺垡辛庄分洪区淹没面积12.907,km2；有机场后，由于机场防洪堤的作用，该区的淹没面积在近期“45,m3/s方案”时减小到8.561,km2，如表9所示，减小了4.345,km2，减小了34%；远期减小到3.998,km2，减小了8.909,km2，减小了69%．除寺垡辛庄分洪区以外的泛区，淹没面积略有增加．

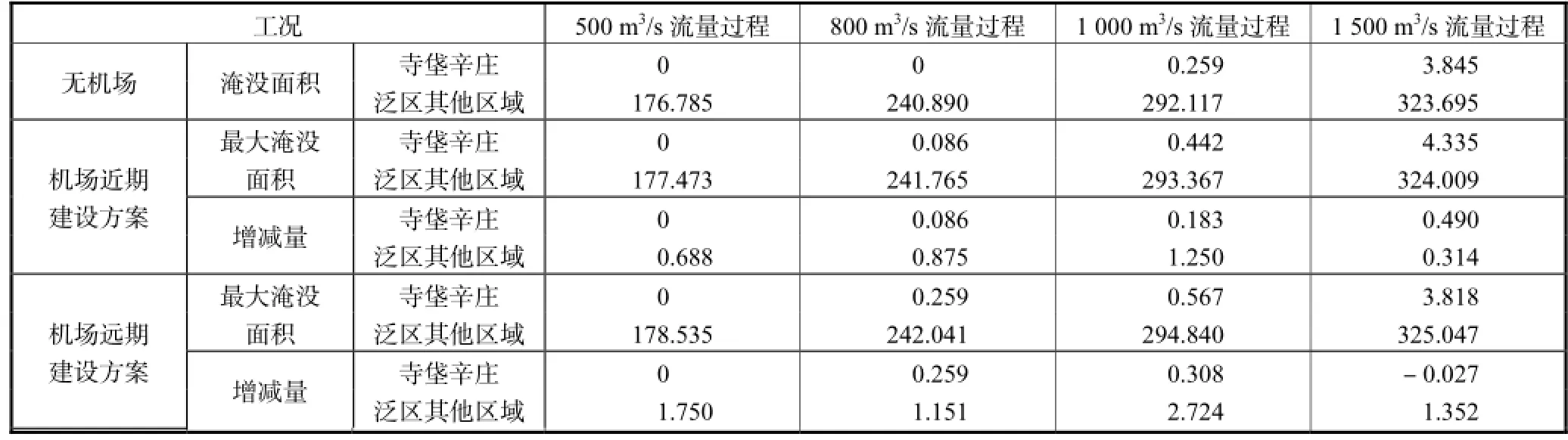
表8 不同工况下中小洪水情况下各方案最大淹没面积Tab.8 The biggest submerged area in small and medium-sized floods under different working conditions km2

表9 100年一遇洪水最大淹没面积及最大滞洪量对比Tab.9 Contrast of the biggest submerged area and amount at one percent flood frequency

5 结论和建议

(1) 通过模型验证和永定河泛区洪水运动趋势分析，说明具有旁侧出流河网独立计算的一二维多口门嵌套衔接模式较好地解决了河道和泛区间多口门分洪的调度问题，可用于河道、泛区洪水调度计算模拟．

(2) 本文最大的特点是建立了一二维嵌套水力模型，更好地适应了多个口门分洪的特点，分别模拟了滞洪区机场建设前后的洪水演进过程，给出了泛区各口门、各特征点的最大流量、最高水位和相应出现时间以及淹没区的淹没面积、淹没水深和淹没历时等洪水风险信息，为进行淹没区的洪灾损失评估及相应的防洪调度决策提供了必要的参数和依据．

(3) 在现行的调度方案中，采用了分区运用、分级调度的方式，以门前水位控制口门的启用使得泛区洪水调度更加具有可操作性，通过明确口门的使用次序，避免仅以流量控制造成口门运用次序的倒置，将会使调度方案更加完善．

(4) 现行的调度方案中对于寺垡辛庄口门没有提及，本次评价也是按门前水位达到现状堤顶高程时自由漫溢来考虑的．新机场建成后，寺垡辛庄口门下的分洪区面积将由原来的35,km2压缩到近期“45,m3/s方案”约11,km2、远期方案约4,km2范围之内．这一区域紧邻机场，关系到机场这一重要防洪对象的安全，因此，其滞洪作用、功能应该给予明确．

(5) 地处下游的西孟村口门的设计进洪水位(16.9,m)偏高，中小洪水很难达到分洪水位，而上游的王玛口门则过早地达到了分洪水位，这种现象将给实施调度带来一定的困难．为此，建议按新地形图进一步调整分洪口门的设计分洪水位，保证上下游、左右岸各个口门之间的水位协调．调整水位时，建议重点研究王玛、潘庄子、西孟村3处口门的水位．

［1］ 李大鸣，管永宽，李玲玲，等. 蓄滞洪区洪水演进数学模型研究及应用[J]. 水利水运工程学报，2011(3)：27-35.

Li Daming，Guan Yongkuan，Li Lingling，et a1. Flood routing mathematical model for flood detention basin[J]. Hydro-Science and Engineering，2011(3)：27-35(in Chinese).

［2］ 李大鸣，林 毅，周志华. 蓄滞洪区洪水演进一、二维数值仿真及其在洼淀联合调度中的应用[J]. 中国工程科学，2010，12(3)：82-89.

Li Daming，Lin Yi，Zhou Zhihua. Research on 1D and 2D numerical simulation of flood routing and its application of combined-regulation in detention basin[J]. Engineering Sciences，2010，12(3)：82-89(in Chinese).

［3］ Caleffi V，Valiani A，Zanni A. Finite volume method for simulating extreme flood events in natural channels[J]. Journal of Hydraulic Research，2003，41(2)：167-177.

［4］ Garcia R，Kahawita R A. Numerical solution of the St. Venant equations with the MacCormaek finite difference scheme[J]. Int J Numer Methods Fluids，1986(6)：507-527.

［5］ 梅亚东，冯尚友. 蓄滞洪区洪水演进模拟[J]. 水利学报，1996(2)：63-67.

Mei Yadong，Feng Shangyou. Flood routing simulation for storage and detention basins[J]. Journal of Hydraulic Engineering，1996(2)：63-67(in Chinese).

［6］ 谢作涛，张小峰，谈广鸣，等. 一维洪水演进数学模型研究及应用[J]. 武汉大学学报：工学版，2005，38(1)：69-72.

Xie Zuotao，Zhang Xiaofeng，Tan Guangming，et al. Study and application of mathematical model for onedimensional flood-routing[J]. Engineering Journal of Wuhan University，2005，38(1)：69-72(in Chinese).

［7］ 谭维炎，胡四一，王银堂，等. 长江中游洞庭湖防洪系统水流模拟(Ⅰ)：建模思路和基本算法[J]. 水科学进展，1996，7(4)：336-344.

Tan Weiyan，Hu Siyi，Wang Yintang，et al. Flow modelling of the middle Yangtze River-Dongting Lake flood control system(Ⅰ)：Modelling procedures and basic algorithms[J]. Advances in Water Science，1996，7(4)：336-344(in Chinese).

［8］ 王船海，李光炽. 流域洪水模拟[J]. 水利学报，1996(3)：44-50.

Wang Chuanhai，Li Guangchi. The model of basin flood[J]. Journal of Hydraulic Engineering，1996(3)：44-50(in Chinese).

［9］ 李 云，范子武，吴时强，等. 大型行蓄洪区洪水演进数值模拟与三维可视化技术[J]. 水利学报，2005，36(10)：1158-1164.

Li Yun，Fan Ziwu，Wu Shiqiang，et al. Numerical simulation and 3-D visualization of flood propagation in large-scale detention basins[J]. Journal of Hydraulic Engineering，2005，36(10)：1158-1164(in Chinese).

［10］ 李大鸣，林 毅，徐亚男，等. 河道、滞洪区洪水演进数学模型[J]. 天津大学学报，2009，42(1)：47-55.

Li Daming，Lin Yi，Xu Ya’nan，et al. Numerical model of flood propagation of rivers and flood dentation basin[J]. Journal of Tianjin University，2009，42(1)：47-55(in Chinese).

［11］ 杨芳丽，张小峰，张艳霞. 一维河网嵌套二维洪水演进数学模型应用研究[J]. 人民长江，2011，42(1)：59-62.

Yang Fangli，Zhang Xiaofeng，Zhang Yanxia. Application of mathematical model of 1-D river network coupled with 2-D horizontal flood routing[J]. Yangtze River，2011，42(1)：59-62(in Chinese).

［12］ 虞邦义，倪 晋，杨兴菊，等. 淮河干流浮山至洪泽湖出口段水动力数学模型研究[J]. 水利水电技术，2011，42(8)：38-42.

Yu Bangyi，Ni Jin，Yang Xingju，et al. Research on hydrodynamic numerical model for main stream of Huaihe River from Fushan to outlet of Hongze Lake[J]. Water Resources and Hydropower Engineering，2011，42(8)：38-42(in Chinese).

［13］ 钱 宁，万兆惠. 泥沙运动力学[M]. 北京：科学出版社，2003.

Qian Ning，Wan Zhaohui. Mechanics of Sediment Transport[M]. Beijing：Science Press，2003(in Chinese).

（责任编辑：樊素英）

Flood Dispatching Numerical Simulation for Detention Basins of Yongding River

Li Daming1，Wang Xiao1，Zhao Mingyu1，Zhang Jianzhong2，Liu Siqing2，Liu Jiangxia2
(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety (Tianjin University)，Tianjin 300072，China；2. Science and Technology Consultation Center of Haihe Water Resources Commission，Ministry of Water Resources，Tianjin 300170，China)

The one-dimensional and two-dimensional linkup model of many diversion entrances nested was put forward，which has independent river network computing with side discharging，and the mathematical model of onedimensional river coupled with two-dimensional horizontal flood routing was established. Combining with the historical flood investigation data，model validation was carried out on the evolution of Yongding river detention basins，and the results are basically consistent with the measured results. The proposed model was applied to the simulation of flood dispatching scheme in Yongding river detention basins，simulating the flood routing process under three working conditions，that is，without the airport，after recent construction and after long-term construction. By analyzing and comparing the variation of flood level，detention volume，submerged area before and after the construction of the airport，the simulation results show that each flood diversion entrance opens earlier，that the opening order of Sifaxinzhuang village diversion entrance changes，and that higher water level，increment of flood diversion and variation of submerged areas have little effect on the dispatching scheme，indicating the feasibility of the airport construction. The study provides necessary parameters and basis for the flood damage assessment of flood inundation area and the amendment of corresponding dispatching scheme.

detention basins of Yongding river；flood routing；one-dimensional and two-dimensionallinkup model；finite volume method

TV122

A

0493-2137(2015)01-0076-11

10.11784/tdxbz201307063

2013-07-19；

2013-09-22.

国家自然科学基金创新研究群体科学基金资助项目(51321065)；河北省水利科研计划资助项目(HS2007-43)．

李大鸣（1957— ），男，博士，教授.

李大鸣，lidaming@tju.edu.cn.