管道复杂流场气固两相流DPM仿真优化

张 涛，李红文,

管道复杂流场气固两相流DPM仿真优化

张 涛1，李红文1,2

(1. 天津大学电气与自动化工程学院，天津 300072；2. 东北石油大学学校办公室，大庆 163318)

针对Fluent中气固两相流离散相模型(DPM)仿真，为提高通用模型对管道节流复杂流场问题仿真时的准确性，在结合气相流场分析与固相颗粒受力分析的基础上，提出DPM优化的4项措施，即从气相速度入口模型、颗粒曳力模型、颗粒壁面碰撞模型、颗粒所受各个力的合理取舍4个方面进行优化．通用模型的优化通过调用Fluent相关宏并编制用户自定义函数(UDF)程序实现．实验已验证优化DPM的准确性明显优于通用DPM，具体体现在：两相流型转换时气相速度区间的模拟，颗粒沉降气相临界速度的模拟方面，这2项指标优化后比优化前分别提高55% 和50% ；在实验管道局部阻力损失与节流孔板前颗粒速度分布的模拟仿真方面，优化DPM显然具有更准确的优势．通过实流实验与仿真模拟的对比，证明优化是有效的．从研究过程可以得出，模型优化的方法对于其他类似的复杂流场工况具有通用性和工程实用价值．

计算流体力学；气固两相流；离散相模型；用户自定义函数；标准孔板

气固两相流在工业生产中，尤其是能源动力及化工等领域应用广泛，其中稀相气固两相流管道流动中，通常安装有流量测量装置，例如燃煤电站输送管道煤粉含量和流量的节流法测量，锅炉工业中含尘烟气流量测量等.近年来林宗虎[1]通过差压法测量气固两相流浓度，即在煤粉吹送管道中加装各种孔板元件来实现，王文琪[2]、谢菲[3]采用文丘里管进行煤粉输送管道中的流量测量.由于节流件的阻碍作用，管道内部流场复杂[4]，流动情况多变.在这种情况下，两相流会有不同流型；如果气相速度降低，固相颗粒还会沉降，因节流件通常用于单相流测量，当用于两相流测量时，需要深入研究上述问题；此外，对固相颗粒轨迹的研究能更好地了解颗粒的行为.这些都有助于提高测量精度.上述问题采用实流实验研究方法显然不十分方便，需要找到一种方便有效的研究方法.

随着计算机仿真应用技术的发展，CFD(computational fluid dynamics)流体仿真模拟技术得到很快的发展，其中Fluent是最有代表性的仿真软件之一，它的优点是突破了实物条件的限制，使用方便，应用范围广泛.DPM(discrete phase model)是Fluent的子系统之一，利用它研究气固两相流离散相实用且有效，可以方便地研究上面提到的这些问题，但在实际应用中发现它仿真模拟的准确性与前文工况或相对应的实流实验有些偏差，准确性尚有提高的可能，仿真的优势未能充分发挥.

本文借助两相流颗粒力学等结论，结合气相流场特点，对离散相颗粒行为进行了详细分析，将颗粒受力进行了合理取舍，结合实际优化了入口与碰撞的边界条件，及曳力系数经验公式，结合UDF(user defined function)这一有力的实用工具，对低浓度气固两相流管道的孔板测量工况的DPM模型进行了改进，即优化研究工作，再通过实流实验进行验证，提高了仿真模拟的准确性.

1 DPM算法的过程分析与数学描述

1.1 Gambit网格剖分与Fluent气相设定

在DPM模型中，定义气体为连续相，定义固体颗粒为离散相.若要准确研究离散相颗粒的行为，气相流场的准确计算与模拟是必要前提.首先依据试验用管道实体情况剖分Gambit网格模型，标准孔板尺寸为D＝50,mm，孔径比β取0.50、0.65、0.75 3种规格，孔板厚度为3,mm，流体介质为标准状况下的空气，孔板前后的直管段长度分别为50D与30D.

孔板前后气相流体湍动剧烈，流场中速度压力梯度大，所以孔板前后网格要划分得精密些，其余直管段部分为流场充分发展段，网格划分相对稀疏些，精密与稀疏网格通过尺寸函数来过渡，这样既能保证网格质量，又不至于使网格数目过多，能平衡好计算的准确性与计算速度的矛盾[5].

仿真计算中，气相控制方程应用Realizable k-ε两方程模型，此模型适用于包含射流，及混合流的管内流动，对本文工况非常适用；设残差小于0.0001时方程收敛；设置求解器为3维单精度形式；动量、湍动能、湍流耗散率等选取一阶差分迎风格式；根据实际将管道入口及出口，设置为速度入口及自由流出口.CFD软件中有网格自适应功能，可根据计算中得到的流场结果反过来调整和优化网格，从而使得计算结果更加准确.计算过程中采用了网格自适应adapt功能[5].

图1为气相仿真中孔板附近轴向剖面速度云图.从图中可见，孔板前1D之前为充分发展的管内湍流，轴向截面速度场形成规则的湍流速度分布.孔板后5D范围以外流场又开始逐渐恢复成孔板射流之前的湍流状态.而在孔板前后，速度与压力梯度大，流场复杂[4]，具体表现为，孔板的射流，形成高速的速度峰值区，孔板两侧的环形直角区又发生剧烈的速度回流，即存在显著的漩涡.

实验用离散相固体颗粒为石英砂，其平均直径0.04,mm，表观密度为2,600,kg/m3，堆积密度为1,400,kg/m3，颗粒形状近似球形．仿真计算中颗粒物性按此进行设置，形状视为球形．

图1 孔板附近轴向剖面速度云图Fig.1 Axial profile velocity contours near the orifice plate

1.2 固体颗粒在气相流场中的受力分析

DPM模型要从颗粒受力作为研究的切入点.离散相颗粒在气相流场运动过程中，重力与浮力是最基本的两个力，此外，还有很多个力作用于颗粒，不同力对颗粒运动影响不同，即地位和作用各有差异[6-7].

颗粒在流场中随气相运动，其惯性力为

式中：dp为颗粒直径；ρp为颗粒密度；up为颗粒速度.在流场中，阻力与曳力二者互为相反，即颗粒对气体产生阻力，曳力是阻力的反作用力，由气体施加于颗粒，其表达式为

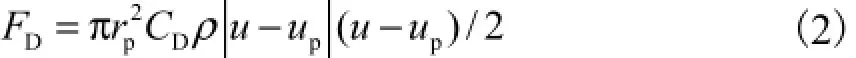
式中：u为气相流体速度；ρ为流体密度；rp为颗粒半径；CD为曳力系数或阻力系数.

这一表达式是定义形式，在具体工程应用中，这一公式会有各种不同表达方式.

压力梯度力是气相流场中压力梯度对颗粒引起的作用力，表达式为

式中Vp为颗粒体积．

由颗粒表观质量效应产生的虚假质量力为

颗粒在流体中旋转会产生升力，称作Magnus升力，它一般与重力数量级相同，表达式为

式中ω为颗粒自转角速度.

流场具有速度梯度，于是颗粒上下侧的速度大小不同，这对颗粒产生的升力，称作Saffman升力，表达式为

式中μ为空气的动力黏度.

在黏性流体中，流体流动的不稳定造成一种瞬时流动阻力，即Basset力，它是一种历史力，需要计算颗粒的运动时间经历的有关指标，才能准确描述.其理论表达式为

1.3 通用DPM模型的解算过程

模型中假设固相的体积分数小于10%，即离散相很稀疏，认为颗粒与颗粒之间，不发生碰撞，没有互相作用.每个颗粒只与流体互相作用.模型的解法是对连续相流体求解欧拉坐标系下的纳维-斯托克斯方程，不失一般性，可先设残差为0.005或0.010，当计算结果收敛后，将颗粒注入流场，再以单颗粒为对象在拉格朗日坐标系下，求解颗粒运动状态，以颗粒的轨道方程来表示，此时要考虑颗粒与流体的相互作用，此时残差一般设为0.000,1，当计算再次收敛时，即得到计算结果.

在DPM中，为求解离散相颗粒运动轨道，需要对描述颗粒作用力的微分方程进行积分.根据牛顿定律，颗粒惯性等于作用在颗粒上的各个力之和，其在直角坐标系下的形式(以x方向为例)为

式中：m为单颗粒质量；Fx是x轴方向上的其他力，包括第1.2节提到的所有力，后文会详细分析这些力的处理方法；Rep为颗粒雷诺数或相对雷诺数，定义为

Fluent中对于Rep有5种经验公式模型可选，通用DPM一般采用的简化表达式为

式中1μ、2μ、3μ、η为DPM通用模型库中存储的常数，由相关经验公式得出．

对式(8)积分可得颗粒轨道x轴方向上每一个点的瞬时速度，而颗粒轨道通过对方程

进行积分，即求得x值．

求得颗粒在x轴方向上的坐标后，同理可求得颗粒在y、z轴方向的坐标，这样仿真计算结果就可得出颗粒在流场中的位置，即离散相颗粒的轨迹．

2 通用DPM的分析与优化

2.1 通过分析确定通用模型的优化策略

通用DPM，也称之为基本或理想DPM模型，适用于很多两相流工况，它普适性较强，但对于某些特殊问题的数值模拟，误差稍大.对于文中气固两相流孔板检测这一具体问题，前文已提及，在孔板前后气相流场很复杂，速度和压力梯度大，固体颗粒受其作用，在孔板前后区域，颗粒与管壁、孔板迎流面发生多次碰撞反弹，由于颗粒自身快速地自转，决定了被反弹后的运动方向也各不相同，当气相速度降低，颗粒还会因重力沉积在孔板前方的管壁下侧，此时气相速度为固相颗粒沉积临界值.因此，对此问题的DPM仿真，需要自定义其中的一些物理模型，以提高针对具体工况模拟的准确性.研究后发现针对本系统，通用模型具有几个方面可以改进和优化之处，详细论述如下.

2.1.1 颗粒受力分析与处理方案

针对第1.2节中颗粒所受各个力，进行分析并选取合适的方案处理，用以优化DPM模型.

通常，颗粒曳力最明显也最大，它比压力梯度力大3个数量级，比虚假质量力比大3或4个数量级[7]，所以，可以合理地忽略这2种较小的力.

通用DPM模型中，设置了Saffman升力处理程序，通过启动相应功能选项来实现.通常的模拟中往往忽略此力，但对本文工况，这样处理有失准确.原因是，根据式(6)分析，Saffman升力由于颗粒上下侧的速度大小不同，即速度梯度所产生，在管道流动的中心区，流体速度梯度小，此力可视为0，但是在边界层中流体速度梯度大，Saffman升力明显，尤其在管内流场复杂的孔板前后方，速度梯度更大.只有对此力加以计算，才能更准确地描述颗粒行为.

通用DPM模型将颗粒看作表面光滑的球形，于是认为颗粒不受气相流场的外力矩，故而合理地将Magnus升力忽略.事实上，颗粒形状不存在理想的球形，只要外形有一点不规则，气相流场就令颗粒受到方向各不相同的力矩作用，结果是颗粒产生自转运动且速度很高[7-8]，经研究发现转速可达1,000,r/s左右.又根据式(5)，Magnus升力大小与重力相比，二者大小相等方向相反，研究得到的几个典型经验值认为二者量值差异在10%以内[7]，于是Magnus升力与重力能够互相抵消.而颗粒的曳力又比重力大1个数量级，由于式(8)中已经计算了重力，如果忽略Magnus升力将会造成很大的误差.所以准确计算此力将更加准确描述颗粒运动.

如果需要准确计算Basset力，需按照由长福等[9]给出的表达式进行.针对本文工况，由湍流引起的颗粒随机脉动，其影响经积分后Basset力几乎为0.同时实际情况也符合流体密度与颗粒密度之比小于0.002时，可以忽略Basset力这个条件，据此本文将其忽略，不失合理性.

2.1.2 仿真模型气相入口速度的优化

模拟管道的气相速度入口时，从图2(a)可见，入口截面上往往采用简化的匀速固定速度流入方式，其大小为u0，而实际上孔板节流件之前已经有足够长的直管段，气相已经形成如图2(b)所示的速度分布.而在通常仿真中，研究人员所设定的入口速度u0是一个通过质量流量准确计量而求得的平均流速，这种简化的速度入口形式与实际情况相差较明显.尤其涉及到计算颗粒轨道的步骤时，气相的差异造成入口处颗粒运动的初始状态就与实际工况有明显差异，尤其是接近于管壁处的边界层区域，这种差异要比管道主流区明显得多.尽管这个差异的影响随着迭代计算会有所减弱，但很难消除，会在整个计算区域一直存在，根据式(6)可知，这种影响的表现之一就是Saffman升力不准确.解决这个问题的方法是采用自定义速度入口，用以描述图2(b)的两相模型气相速度入口形式为

式中：R为圆形管道半径，R＝25,mm；um为圆形管道中心轴线上的速度；uin为管道入口处距轴线r处的速度，针对本文工况，经流体力学基本理论计算，可知um＝1.24,u0，采用式(12)描述的气相速度入口，可提高仿真计算的准确性.

图2 两种仿真模型速度入口形式Fig.2 Speed entry of two kinds of simulation model

2.1.3 颗粒曳力模型的选择

在计算曳力时，通用DPM模型给出的5个经验公式，编制了相应程序，用来解决各种常见工况.在一定的颗粒雷诺数Rep范围内，程序中通常用将CD表示为Rep的一个全区域通用的经验公式函数.而在本文工况中，对于充分发展的管内流动，雷诺数变化范围较大；尤其在孔板前后附近区域，即孔板前1倍后3倍管径范围内，气体湍动显著，雷诺数的变化区间超过充分发展管流的数倍，颗粒受气相流体作用，造成全区域的曳力系数模型较为粗略，针对此问题有必要选择更加准确的曳力系数模型.

在计算方程(8)时，CD采用文献[7]提供的“球形颗粒曳力系数表达式”，它将见整个颗粒雷诺数适用范围分为10个区间，如表1所示，它来源于前人大量的实验数据与统计研究，从0到无穷大的任何一个颗粒雷诺数，都相应地对应某个精确的曳力系数表达式，其优点在于采用分段表示的的精确公式，准确性明显要高于全区域通用的经验公式.在DPM模型优化中，为提高仿真模拟的准确性将表1公式组代替原有的曳力系数表达式.

表1 全雷诺数范围球形颗粒曳力系数表达式Tab.1 CDof full range Repon spherical particle

2.1.4 颗粒壁面碰撞边界条件优化

系统运行中，固体颗粒会与壁面发生碰撞并反弹，尤其在孔板迎流面最为显著.碰撞行为受颗粒的物性、运动状态，包括速度、入射角度，自旋状态等等参数的影响，由于众多因素的影响，至今没有反映碰撞规律的普适模型，在DPM通用模型中，程序将实际情况简化为反射、捕获、逃逸3种边界条件，这样处理的理由有2点，或是认为颗粒碰撞不存在能量损失，是完全的弹性碰撞，或是简单地设定一定的常数值碰撞恢复系数，用以表示颗粒的能量损失程度.分析可知，这2个简化方法都不能较准确描述颗粒与壁面碰撞的复杂过程，引入计算误差.所以要针对各个工况的具体情况寻求合理的碰撞模型，便于准确地描述碰撞后颗粒的行为，以及描述更为准确的运行轨迹，从而提高仿真准确性.

国内外一些科研人员[8，10-11]通过激光全息和PIV实验装置，针对于某些特定的工作参数条件.得到了一些颗粒壁面碰撞模型的经验公式，这些经验公式普遍认为反射、捕获、逃逸的定义，稍为简单，他们通过大量的统计性研究，发现恢复系数与入射角及入射速率有关.本文中颗粒的理化特性与工况非常接近其应用条件，故将其应用于DPM模型优化过程中文献[8]所提供经验公式为

式中：v1与v2分别为颗粒与壁面碰撞前后的速率；α1与α2分别为颗粒的入射角与出射角，rad．具体形式如图3所示．

图3 颗粒壁面碰撞示意Fig.3 Collisions between particles and wall

2.2 DPM优化策略的实现

Fluent软件不可能满足每一个具体工况的实际情形，其标准界面及功能并不能满足每个用户的需要．软件提供的UDF功能正是为解决这个问题而开发的，用户可以编写Fluent源代码来满足各自的特殊需求．用户自编的代码程序可以动态地链接到Fluent求解器上来提高求解器性能．UDF中可使用标准C语言的库函数，并使用Fluent提供的预定义宏，通过预定义宏，可以获得Fluent求解器中的数据．本文采用编译型UDF，嵌入共享库中与Fluent链接并运行[5]．

采用UDF功能实现通用DPM模型的优化，采用上文相关公式进行C语言编程，并通过Fluent中的几个自定义宏来实现，对应第2.1节相关宏如下．

(1)为准确计算Magnus升力，使用“自定义重力及曳力之外的其他体积力”这个宏，其语句为DEFINE_DPM_BODY_FORCE；如需准确计算Basset力，也通过这一宏实现.

(2)为准确定义空气入口湍流速度剖面表达式，使用“自定义边界截面上的变量分布”这个宏，其语句为DEFINE_PROFILE.

(3)为定义颗粒曳力模型的公式组，使用“自定义流体中颗粒的曳力系数”这个宏，其语句为DEFINE_DPM_DRAG.

(4)为实现自定义的颗粒与壁面碰撞规律.使用“自定义颗粒到达边界后的状态”这个宏，其语句为DEFINE_DPM_BC.

所编制的C语言源程序，包含上述宏语句的代码，在离线调试运行成功后，作为功能模块添加到Fluent通用模型中，然后再进行DPM模拟计算，这样，针对气固两相流节流流场，拓宽了通用DPM模型适用范围，同时提高了仿真精度，解决了具体问题的实际需求，DPM模型得以优化.

需要说明一点，Fluent中DPM优化前后，其适用条件没有变化，即假定离散相非常稀疏，这样可以合理地忽略颗粒与颗粒间的相互作用，以及忽略颗粒体积对连续相的影响．这个假定意味着离散相体积分数小于10%．但是颗粒质量载荷可以远大于10%．在下文的实验与仿真中，当取最大的固气质量比RPG＝5时，颗粒体积为两相混合物的0.43%，符合DPM的适用条件．在仿真计算中，颗粒载荷比较大，离散相的颗粒质量会对连续相气体的流动状态产生影响，所以为准确计算两相间的相互作用，需采用相间耦合计算模式[12]．

3 DPM优化前后仿真与实验对比验证

实流实验在天津大学气固两相流实验装置上完成，此装置是研究气固两相流的理想平台，实验段管路可以安装各种流量检测仪表．装置详细介绍可见文献[13]．实验台部分接入标准孔板法兰取压部件，法兰两端可以更换，实验中接入一段粗糙度等指标与钢质管道很接近的透明工程塑料管道，以便观察管内孔板前后颗粒的流动状况．

3.1 气固两相流流型与流型转换区间的验证

实验中，针对3种不同规格孔板，当固体颗粒注入，在β＝0.50、0.65、0.75时，气固质量比RPG＝1.0、2.0、3.0，固相体积分数均小于0.25%，此时两相流有悬浮流和管底流2种流型，分别描述为：①气相作用下，所有颗粒悬浮在管道中向前流动，颗粒在管道中呈现均匀的弥散状态，此时处于悬浮流状态；②半数以上的颗粒位于管道下部高度为D/4部分，在气相作用下，少数颗粒在管道底部跳跃前进甚至滚动(或滑动)前进，此时颗粒处于管底流状态，而颗粒未出现停滞，全部流过管道，没有沉积在管道底部．当气相入口流速改变时，流型会有所变化，速度较低时出现管底流，速度较高时，出现悬浮流．两种流型之间有一个过渡区域，文中称为流型转换区．实验操作中，气相入口的速度u0的范围为2～10,m/s．入口速度u0从高速开始，逐步减小，每隔0.1,m/s为1个实验点．这样得到实际实验中流型转换速度区间[u1，u2]，当u0＞u2时是悬浮流，当u0＜u1时是管底流．颗粒流动的状况可以从孔板前方的透明管道观察到．

仿真采用ANSYS Fluent13版本软件，设定与实流实验相同的实验点参数．先对每个实验点工况下进行纯空气流动的仿真模拟，当气相收敛残差达到0.01时，暂停仿真，存储cas与dat文件，为进行比较研究，分别启动通用DPM模型，与优化DPM模型进行仿真，便于比较研究．在颗粒注入管道气相流场时，采用管道入口的面射流源注入．

图4为DPM仿真程序模拟绘制出的颗粒轨迹(统计平均轨道)，分别代表了2种流型．在孔板上游，处于悬浮流的颗粒轨迹均匀地布满整个管道剖面，处于管底流时颗粒在管道下方更为密集，与孔板迎流面下方发生碰撞也多一些，这与实验管道中的观察情况一致．

通过仿真与实验结果对比可知，优化DPM在两个方面优于通用DPM：①通过观察可知，优化后模型仿真模拟颗粒的轨迹更接近实际情况；②流型转换时，对气相临界速度区间的模拟，优化模型更接近于实流实验，如表2所示，仿真结果的平均偏差约为优化前的45%．

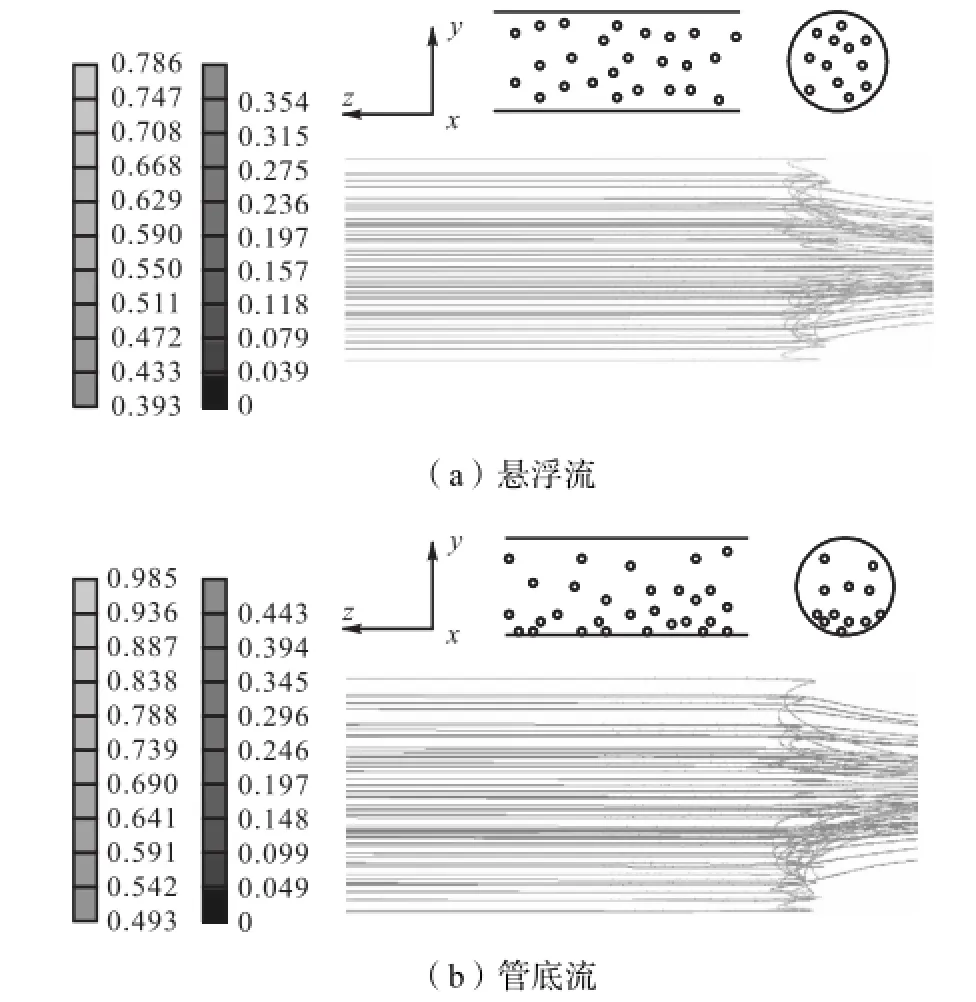
图4 悬浮流与管底流实物与仿真示意(单位：s)Fig.4 Suspension flow and pipe bottom flow(unit：s)

仿真结果偏差是按如下方法估算的：取每个速度区间的中点，作为流型转换区速度的典型值，以表中第1行数据为例，相应的各个典型值为5.90、5.40、5.55，以实流实验为准，通用与优化DPM仿真典型值相对于实验典型值的偏差大小分别为δc＝0.35和δo＝0.15，于是优化DPM相对于通用模型对比，典型值偏差减小为优化前的比例为Δ＝δo/δc＝0.428． m/s

表2 流型转换时气相速度区间[u1，u2]Tab.2 Velocity conversion range [u1，u2] of air flow

这组实验在不同时间做过3次(每次实验数据都与表2非常接近)，一共9组数据，相应算出9个Δ值，这9个Δ的算术平均值是0.45，所以得到仿真结果的平均偏差约为优化前的45%．如果在数轴上观察各个区间的分布情况，能够看出优化DPM所描绘的转换区间明显比通用DPM接近实流实验．

3.2 颗粒沉降气相临界速度的仿真与实验

在流型为管底流状态时，当气相入口速度逐渐降低时有更多的颗粒在管底滚动(或滑动)前进，越多的颗粒碰撞管底后不会弹起，速度进一步降低，有部分颗粒因速度不足而不能通过孔板，滞留在孔板前部的管道下方及孔板前部直角区的位置．这种工况可以在实验装置透明管道中观察到．当有颗粒滞留时，气相入口速度称为颗粒沉降的气相临界速度，这一量值是本节实验与仿真所研究的对象．

因DPM颗粒轨迹曲线是跟踪计算程序由统计平均所得到的一簇平均轨道，颗粒对管壁的小角度撞击反弹与在管底悬浮或滚动(或滑动)行为之间不易区分，研究中发现存在一个角度阈值α0，在式(14)中相关程序定义α0＞α2时，颗粒撞击管底后不会弹起，而是在管底壁面上滚动(或滑动)前进，此时如果气相速度相对高些，颗粒会再次被吹起，流过孔板，而当气相速度较低时，就易于出现因速度不足而滞留在管道底部的沉降工况．在实验中发生沉降现象的速度点两侧，流量点每隔0.05,m/s进行仿真对比，得到DPM模型优化前后沉降时气相临界速度仿真与实验对比结果，优化后颗粒沉降气相临界速度平均偏差量减小为优化前的50%，这组实验同样在不同时间做过3次，表3是其中具有代表性的一次数据，共得9组数据，偏差量的计算方法同第3.1节．

表3 颗粒沉降气相临界速度Tab.3 Air critical speed of particle settling

另外还需说明，经过仿真可知，3块不同孔板对应的阈值α0有所不同，当孔板β＝0.50、0.65、0.75时，α0的取值分别为4.5°、4.0°、3.0°．

3.3 孔板前后阻力损失的验证

将气固两相流中的颗粒群运动，视为一种特殊的流体，两相流在实验管道中流动，受到摩擦阻力与局部阻力，后者为孔板节流导致的旋涡造成的阻力损失．这2种阻力损失的大小，可以按照下面方法测量：将实验段管道中孔板前50,mm至孔板后950,mm的管道部分，作为实验段．如果不加装孔板，所测量的阻力损失就是这段管道的摩擦阻力损失；加装孔板后，测量值为管道摩擦阻力损失与孔板局部阻力损失之和．孔板厚度仅有3,mm，可以完全忽略长度为3,mm管段上的摩擦阻力损失．

在这个实验管段之前已经有足够长的直管段，气体与颗粒已经发展成为管内匀速流(空气及颗粒的流动速率都为定值)．在孔板前50,mm作为实验段的起点，两相流在流经孔板经节流后，在孔板后10D (500,mm)已恢复成为管内匀速流，颗粒在管道内无滞留，所以取孔板后950,mm处作为实验段的终点是合适的，两端的气体与颗粒流动的速率相等．这样可以将阻力损失用两端的压力降(表压降)来衡量，这样便于仿真与实验对比验证．实验与仿真对比中，取2个典型的气相速度入口平均值(u0)为10,m/s与5,m/s，10,m/s是悬浮流状态，5,m/s是从悬浮流到管底流的转换状态．

仿真与实验结果如下，对于实验段管道，未加装孔板，从图5中可见，横坐标为固气质量比RPG，DPM仿真优化前后，摩擦阻力损失数值差别不大，2条曲线基本重合，实验与仿真产生一定的差别，经分析可知，是属于仿真中的模型误差，例如：管道模型内壁粗糙度设置与实际的差异，仿真算法的数学描述与实际工况的差距，以及仿真计算多次迭代运算产生的舍入误差等原因造成，这属于仿真的系统误差.

图5 阻力损失对比(u0＝10,m/s，直管段，悬浮流)Fig.5Resistance loss(u0＝10,m/s，straight pipe，suspension flow)

这个工况下，DPM优化前后基本没有区别．而将实验速度点逐步降低，如8,m/s，6.5,m/s，直到5,m/s，所得到的各组曲线，除了阻力损失数值有所不同外，曲线的变化趋势都与图5十分类似，图6中所示气相入口速度为5,m/s．

当加装孔板进行节流测量时，摩擦阻力损失与未加装孔板时大小相同．研究局部阻力损失，取空气入口速度为10,m/s及8,m/s(均为悬浮流)，从图7可以得出，曲线趋势与图5相似．优化DPM模型的优越性没有体现．但是当速度逐步降低进入流型转换区间后，优化DPM的准确性得以体现，如图8所示．

图6 阻力损失对比(u0＝5,m/s，直管段，流型转换区)Fig.6Resistance loss(u0＝5,m/s，straight pipe，flow pattern transition area)

图7 局部阻力损失对比(u0＝10,m/s，安装孔板，悬浮流)Fig.7 Local resistance loss(u0＝10,m/s，orifice plate installed，suspension flow)

图8 中，气相入口速度为5,m/s，仿真对比发现，优化DPM对阻力损失的模拟明显较通用DPM接近实验值．分析其原因，在孔板复杂流场情况下，优化后DPM对颗粒行为(速度、动量的大小和方向)的模拟更接近于实际情况．并呈现如下规律：固气质量比越大，优化后DPM对阻力损失的模拟准确性越明显.

图8 局部阻力损失对比(u0＝5,m/s，安装孔板，流型转换区)Fig.8 Local resistance loss(u0=5,m/s，orifice plate installed，flow pattern transition area)

图5 ～图8中，所用孔板规格是β＝0.75，当用其他2块孔板实验时，除了阻力损失的数值有所变化外，曲线的趋势与图5～图8一致．这充分说明，优化后的DPM，在管底流到悬浮流的转换区间中对颗粒行为的模拟，在局部阻力损失的准确性上有较明显的提高，经过仿真比较可知，主要原因在于优化DPM后碰撞模型的合理选取，其次是Saffman升力与Magnus升力的处理．在转换区间内，有如下趋势：气体和颗粒的流动速率越小，固气质量比越大，优化DPM对局部阻力损失模拟的准确性越明显，而且孔板的β值越小，优化DPM模型的准确性越明显．

3.4 固相颗粒通过孔板前的速度分布仿真

实验管道系统是相对封闭的，管道中无颗粒沉积，所有的颗粒全部流过孔板，DPM软件给出的颗粒速度，是Fluent软件计算得出的统计平均速度值(轴向流动的速率)．考察孔板前面0.5D处的速度分布，能说明DPM优化后的准确性优势．

孔板前部法兰取压点的轴向剖面速度如图9所示(悬浮流状态u0＝8,m/s，RPG＝1.0，β＝0.75)．仿真中当固气质量比RPG从1.0增加至4.0时，颗粒速度分布曲线一直与图9类似．这说明颗粒处于悬浮状态时，DPM优化前后对颗粒速度的模拟基本一致．曲线纵轴坐标为经过管道中心的纵向截面的位置，区间为[－25,mm，25,mm]．曲线横轴坐标为颗粒的速率(轴向速度值)．DPM优化前后所描绘出的速度曲线，其速度峰值的位置基本位于管道的中心轴线上，曲线关于中心轴对称．

图9 孔板前取压点的轴向速度分布(u0＝8,m/s，RPG＝1.0)Fig.9Axial velocity distribution at orifice upstream pressure point(u0＝8,m/s，RPG＝1.0)

当降低气相入口速度，取u0为5,m/s时，图10为RPG＝1时的颗粒速度分布曲线．从曲线中可知，优化后的DPM所描绘出的曲线，其速度峰值所在位置要比通用DPM相应的位置稍高，出现“峰值上扬”的现象．结合前面第3.1节的分析，可知优化后曲线更符合实际实验的情况，这是由于以下2个原因造成的：①颗粒与管壁及孔板迎流面撞击后，各个颗粒速度大小与方向多变，因孔板的阻滞，造成一部分颗粒会逆向回流，所以轴向流动速率减小．因颗粒流态处于从悬浮流向管底流转换区间中，此时管道下半部的颗粒浓度大，与管壁、孔板迎流面发生撞击的次数多，轴向流动速率变小，这符合轴向速率“峰值上扬”的现象；②由于颗粒浓度大，管内匀速流动的空气推动颗粒运动，管道下半部空气的负载比上半部大，于是下半部颗粒速度小．经仿真与实验可知2个因素比较，原因①更为显著．

图10 孔板前取压点的轴向速度分布(u0＝5,m/s，RPG＝1.0)Fig.10Axial velocity distribution at orifice upstream pressure point(u0＝5,m/s，RPG＝1.0)

当固气质量比进一步增大，取RPG＝4.0时，颗粒速度的分布如图11所示．从图11中可见，图中所描绘出的颗粒速度分布，相应各点速率值比图10中有所降低，这是固相含率增加，空气负载增大所致，优化DPM中“峰值上扬”现象稍加明显，这符合上面的分析．

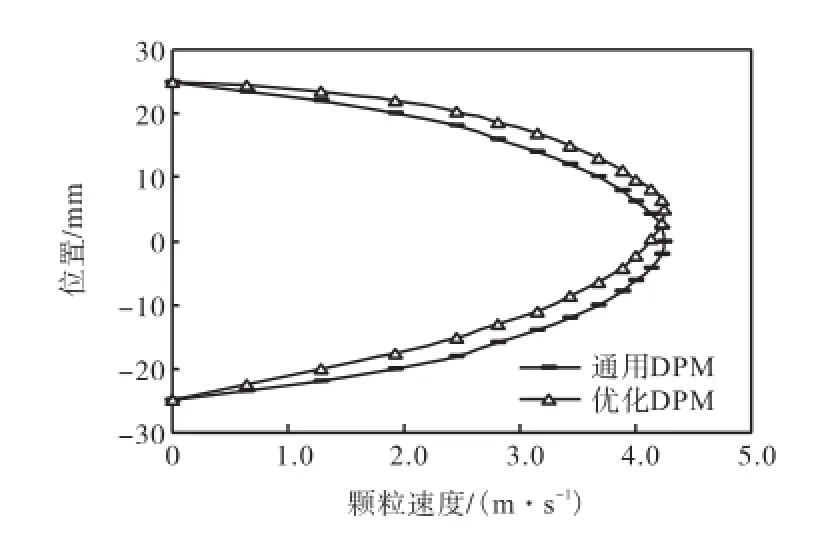
图11 孔板前取压点的轴向速度分布(u0＝5,m/s，RPG＝4.0)Fig.11 Axial velocity distribution at orifice upstream pressure point(u0＝5,m/s，RPG＝4.0)

在针对流型转换区间的实流实验中，气相入口速度逐步降低，颗粒速度“峰值上扬”现象是逐渐出现的，从上面的速度分布定量分析，结合第3.1节中的实验，可知在转换区间内颗粒经过了在管道中上半部浓度逐渐减小、下半部浓度逐渐增加，上半部轴向速度越来越稍高于下半部速度、这样一个逐渐变化的过程，主要是由于管道下半部颗粒与管壁及孔板多次碰撞反弹的行为更加显著造成的，优化DPM仿真的结果符合于这个过程，而通用DPM的仿真数据，在气相入口速度u0低于5,m/s后，才开始出现“峰值上扬”现象，而又比实流实验早一些离开流型转换区间而接近颗粒沉降的状态．从颗粒受力结合仿真分析可知，通用DPM弱化或者忽略了Saffman升力与Magnus升力的效应．这是优化DPM准确性更接近实流实验的主要原因之一．

同时通用DPM中，颗粒与壁面碰撞的处理也过于简化，通用DPM认为，颗粒小角度或者低速度撞击管壁，就会被管壁粘附，模型中称为颗粒被壁面“吸收”，从而出现沉降的趋势，而事实上，由于气相流场的复杂性，即使被“吸收”，具有沉降趋势的颗粒也会再次被气相湍流吹起而继续向下游运动.所以这是其仿真计算精度稍低于优化DPM的另一个主要原因．

取β＝0.65与0.50，u0＝5,m/s、8,m/s和RPG＝1.0、2.0、3.0各个工况下的仿真结果与图9～图1,l类似，优化DPM合理地模拟了管道剖面颗粒速度分布的“峰值上扬”现象．这同样证明优化后的DPM更接近于实际，对DPM的优化是有效的．

4 结 语

本文通过对通用DPM进行优化，得到了理论仿真与实流实验相一致的结果．仿真与实验证明，对气固两相流流型转换区间及颗粒沉降气相临界速度的模拟两方面，优化DPM仿真的准确性明显高于通用DPM，准确性提高了55%和50%．再通过对孔板局部阻力损失及孔板前法兰取压点速度分布的仿真与实验对比分析得出：在流型转换区间的模拟方面，优化DPM比通用DPM更接近于实流实验．通过对优化DPM的研究，深化了对管道节流两相流颗粒行为的了解，有助于更准确分析两相流测量工况，提高测量精度．研究过程中，将理论及经验公式通过编程与宏命令灵活结合，形成UDF模块并嵌入Fluent仿真程序中的方法，是理论模型得以实现的关键所在．

研究过程虽然是基于孔板节流管道得出，但具有代表性，思路和方法可用于类似具有节流特点和复杂流场的两相流工况中，在工程上具有实用性.

［1］ 林宗虎. 能源动力中多相流热物理基础理论与技术研究[M]. 北京：中国电力出版社，2010.

Lin Zonghu. Basic Theory and Technology of Multiphase Flow Thermophysics in Energy and Power Engineering[M]. Beijing：China Electric Power Press，2010(in Chinese).

［2］ 王文琪，侯 明，于荣宪. 用长颈文丘利管测量气固两相流量[J]. 东南大学学报，1989，19(5)：82-87.

Wang Wenqi，Hou Ming，Yu Rongxian. Measurement of gas solid flow rate with an extended-throat Venturi tube[J]. J Southeast Univ，1989，19(5)：82-87(in Chinese).

［3］ 吴占松，谢 菲. 用于管道煤粉流量测量的文丘里管型设计及优化[J]. 清华大学学报：自然科学版，2007，47(5)：666-669.

Wu Zhansong，Xie Fei. Optimization of Venturi tube design for pipeline pulverized coal flow measurements [J]. Journal of Tsinghua University：Science and Technology，2007，47(5)：666-669(in Chinese).

［4］ 陈家庆，王 波，吴 波，等. 标准孔板流量计内部流场的CFD数值模拟[J]. 实验流体力学，2008，22(2)：51-55.

Chen Jiaqing，Wang Bo，Wu Bo，et al. CFD simulation of flow field in standard orifice plate flow meter[J]. Journal of Experiments in Fluid Mechanics，2008，22(2)：51-55(in Chinese).

［5］ 李鹏飞，徐敏义. 精通CFD工程仿真与案例实战[M]. 北京：人民邮电出版社，2011.

Li Pengfei，Xu Minyi. Proficient in Operating on CFD Simulation Case[M]. Beijing：Posts and Telecom Press，2011(in Chinese).

［6］ 车得福，李会雄. 多相流及其应用[M]. 西安：西安交通大学出版社，2007.

Che Defu，Li Huixiong. Multiphase Flow and Its Application[M]. Xi'an：Xi'an Jiaotong University Press，2007(in Chinese).

［7］ 岑可法. 工程气固多相流动的理论和计算[M]. 杭州：浙江大学出版社，1990.

Cen Kefa. Engineering Theory and Calculation of the Gas-Solid Multiphase Flow [M]. Hangzhou：Zhejiang University Press，1990(in Chinese).

［8］ 施学贵，徐旭常，冯俊凯. 颗粒在湍流气流中运动的受力分析[J]. 工程热物理学报，1989，10(3)：320-325.

Shi Xuegui，Xu Xuchang，Feng Junkai. The analysis of force on particles moving in turbulent flow[J]. Journal of Engineering Thermophysics，1989，10(3)：320-325(in Chinese).

［9］ 由长福，祁海鹰，徐旭常. Basset力研究进展与应用分析[J]. 应用力学学报，2002，19(2)：31-33.

You Changfu，Qi Haiying，Xu Xuchang. Progresses and applications of Basset force[J]. Chinese Journal of Applied Mechanics，2002，19(2)：31-33(in Chinese).

［10］ Di Maio F P，Di Renzo A. Analytical solution for the problem of frictional-elastic collisions of spherical particles using the linear model[J]. Chemical Engineering Science，2004，59(16)：3461-3475.

［11］ 饶 江，葛满初，徐建中，等. 固体颗粒与通道壁面相互作用的实验研究[J]. 工程热物理学报，2003，24(1)：134-136.

Rao Jiang，Ge Manchu，Xu Jianzhong，et al. Experimental investigation on interaction between solid particle and wall surface[J]. Journal of Engineering Thermophysics，2003，24(1)：134-136(in Chinese).

［12］ 于 勇，张俊明，姜连田. Fluent入门与进阶教程[M]. 北京：北京理工大学出版社，2008.

Yu Yong，Zhang Junming，Jiang Liantian. Introductory and Advanced Tutorial on Fluent[M]. Beijing：Beijing Institute of Technology Press，2008(in Chinese).

［13］ 王 超，王玉琳，张文彪. 基于静电传感的气固两相流测量及研究装置[J]. 电子测量与仪器学报，2011，25(1)：1-9.

Wang Chao，Wang Yulin，Zhang Wenbiao. Gas-solid two-phase flow measurement and research apparatus based on electrostatic sensing[J]. Journal of Electronic Measurement and Instrument，2011，25(1)：1-9(in Chinese).

(责任编辑：孙立华)

Simulation Optimization of DPM on Gas-Solid Two-Phase Flow in Complex Pipeline Flow Field

Zhang Tao1，Li Hongwen1,2
(1. School of Electrical Engineering and Automation，Tianjin University，Tianjin 300072，China；2. School Office，Northeast Petroleum University，Daqing 163318，China)

General discrete phase model (DPM) simulation on gas-solid two-phase flow is now widely employed. In order to improve its accuracy on pipeline throttling with complex flow field, based on analysis combined gas flow field and forces acting on solid phase particles, four optimization measures about the general DPM model are proposed, which include gas inlet velocity model, particle drag model, collision of particles with internal surface of pipeline and reasonable choice of each force on particles. The optimization of general model is achieved by calling Fluent related macro and compiling user defined functions (UDF) program．Experiments verified that the accuracy of the optimized DPM model is significantly superior to the general model，as is shown in the following four aspects: the simulations of the two-phase flow gas velocity conversion interval and the gas critical velocity of particle sedimentation，which increased by 55% and 50% respectively in the optimized model; what is more, the optimized model obviously has more accuracy advantage on local resistance loss in experimental pipe and particle velocity distribution simulation. Through the contrast of experiment and simulation, the optimization is proved to be successful, and it is concluded that the method of optimization is versatile for other pipeline with complex flow field and has practical engineering value．

computational fluid dynamics；gas-solid two-phase flow；discrete phase model(DPM)；user defined function(UDF)；standard orifice plate

TP391

A

0493-2137(2015)01-0039-10

10.11784/tdxbz201306057

2013-06-27；

2013-11-08.

国家高技术研究发展计划(863计划)资助项目(2007AA04Z180)；国家自然科学基金资助项目(60974118).作者简介：张 涛（1950— ），男，硕士，教授，zt50@tju.edu.cn.

李红文，lize739@163.com.

时间：2014-03-24.

http://www.cnki.net/kcms/doi/10.11784/tdxbz201306057.html.